- Introduction
- Non 0-dimensional system
- General purpose solving algorithm
- Mathematical background
- The 3B method
- Simplification procedure
- Implementation
- Examples and Troubleshooting
- General purpose solving algorithm with Jacobian
- General purpose solving algorithm with Jacobian and Hessian
- Stopping the general solving procedures
- Ridder method for solving one equation
- Brent method for solving one equation
- Newton method for solving systems of equations
- Krawczyk method for solving systems of equations
- Solving univariate polynomial with interval analysis
- Solving univariate polynomial numerically
- Solving trigonometric equation
- Solving systems with linear and non-linear terms: the simplex
method
- Solving systems with determinants
- Solving systems of distance equations
- Filtering a system of equation
Solving with Interval Analysis
Introduction
The purpose of this chapter is to describe the methods based on interval analysis available in the ALIAS library for the determination of real roots of system of equations and inequalities.
Interval Analysis
Mathematical background
This section is freely inspired from the book [5]. An interval number is a real, closed interval![\begin{eqnarray*}
&&X+Y= [\underline{x}+\underline{y},\overline{x}+\overline{y}]\\
&&X-Y= [\underline{x}-\overline{y},\overline{x}-\underline{y}]
\end{eqnarray*}](img7.png)
An interval function is an interval-valued function of one or more interval arguments. An interval function
A fundamental theorem is that any rational interval function evaluated with a fixed sequence of operations involving only addition, subtraction, multiplication and division is inclusion monotonic. This means in practice that the interval evaluation of a function gives bounds (very often overestimated) for the value of the function: for any specific values of the unknowns within their range the value of the function for these values will be included in the interval evaluation of the function. A very interesting point is that the above statement will be true even taking into account numerical errors. For example the number 1/3, which has no exact representation in a computer, will be represented by an interval (whose bounds are the highest floating point number less than 1/3 and the smallest the lowest floating point number greater than 1/3) in such way that the multiplication of this interval by 3 will include the value 1. A straightforward consequence is that if the interval evaluation of a function does not include 0, then there is no root of the function within the ranges for the unknowns.
In all the following sections an interval for the variable ![]() will be
denoted by
will be
denoted by
![]() . The width or diameter of an interval
. The width or diameter of an interval
![]() is the
positive difference
is the
positive difference
![]() .
The mid-point of an interval is defined as
.
The mid-point of an interval is defined as
![]() .
.
A box is a set of intervals. The width of a box is the largest width of the intervals in the set and the center of the box is the vector constituted with the mid-point of all the intervals in the set.
Implementation
All the procedures described in the following sections use the free
interval analysis package
BIAS/Profil
in which the basic operations of interval
analysis are implemented2.1.
This package uses a fixed precision arithmetics with an accuracy of
roughly ![]() .
Different types of data structure are implemented in this package. For
fixed value number:
.
Different types of data structure are implemented in this package. For
fixed value number:
BOOL, BOOL_VECTOR, BOOL_MATRIX, INT, INTEGER_VECTOR, INTEGER_MATRIX, REAL, VECTOR, MATRIX, COMPLEXfor intervals:
INTERVAL, INTERVAL_VECTOR, INTERVAL_MATRIXAll basic arithmetic operations can be used on interval-valued data using the same notation than for fixed numbers. Not that for vector and matrices the index start at 1:
For the evaluation of more complex interval-valued function there are
also equivalent function in the BIAS/Profil, whose name is usually
obtained from their equivalent in the C language by substituting their
first letter by the equivalent upper-case letter: for example the
evaluation of ![]() where
where ![]() is an interval will be obtained by
calling the function
is an interval will be obtained by
calling the function ![]() . We have also introduced in ALIAS
some other mathematical operators whose names are derived from their
Maple implementation: ceil, floor, round.
. We have also introduced in ALIAS
some other mathematical operators whose names are derived from their
Maple implementation: ceil, floor, round.
Table 2.1 indicates the substitution for the most used functions.
Note also that the mathematical operators
A special operator is defined in the procedure ALIAS_Signum:
formally it defines the signum operator of Maple defined as
which is not defined at
- $$
- 1if
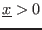
- $$
- -1 if
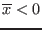
- $$
- 1if
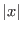 is lower than ALIAS_Value_Sign_Signum and
ALIAS_Sign_Signum is positive
is lower than ALIAS_Value_Sign_Signum and
ALIAS_Sign_Signum is positive
- $$
- -1 if
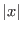 is lower than ALIAS_Value_Sign_Signum and
ALIAS_Sign_Signum is negative
is lower than ALIAS_Value_Sign_Signum and
ALIAS_Sign_Signum is negative
- -1,1
- otherwise
The derivative of ALIAS_Signum is defined in the procedure
ALIAS_Diff_Signum.
Formally this derivative is 0 for any ![]() not equal to 0. In our
implementation ALIAS_Diff_Signum(
not equal to 0. In our
implementation ALIAS_Diff_Signum(![]() ) will return 0 except if
) will return 0 except if
![]() is lower than ALIAS_Value_Sign_Signum in which case the
procedure returns [-1e11,1e11].
is lower than ALIAS_Value_Sign_Signum in which case the
procedure returns [-1e11,1e11].
The derivative of the absolute value is defined in the procedure ALIAS_Diff_Abs. If the interval X includes 0 the procedure returns [-1e11,1e11] otherwise it returns ALIAS_Signum(X).
Using the above procedures
when an user has to write an interval-valued function he has to
convert its C source code using the defined substitution. For example
if a function is written in C as:
then its equivalent interval valued function is
A special care has to be used when transforming an equation into its interval equivalent. The formulation may play a role in the efficiency. For example you should avoid as much as possible multiple occurences of the same variable as this will usually lead to an overestimation of the interval evaluation. For example
Note that all the even powers of an interval are better managed with
the Sqr and Power procedures. Indeed let consider the
interval ![]() , then the interval product
, then the interval product ![]() leads to the
interval [-1,1] while the interval Sqr(
leads to the
interval [-1,1] while the interval Sqr(![]() ) leads to [0,1].
For an interval
) leads to [0,1].
For an interval
![]() the width of the interval is obtained by
using the procedure Diam(
the width of the interval is obtained by
using the procedure Diam(![]() ) while we have
) while we have
![]() Inf(
Inf(![]() ) and
) and ![]() Sup(
Sup(![]() ).
).
We will denote by box a set of intervals which define the possible values of the unknowns. By extension and according to the context boxes may also be used to denote a set of such set. A function intervals will denote the interval values of a set of functions for a given box, while a solution intervals will denote the box which are considered to be solution of a system of functions.
Problems with the interval-valuation of an expression
An important point is that not all expressions can be evaluated using interval arithmetics. Namely constraints that prohibits the interval evaluation of an expression are:
- denominator that may include 0
- argument of square should be positive
- argument of arcsin and arccos should be included in [-1,1]
- argument of log,ln,log10 should be positive
- argument of arccosh should be greater than 1
- argument of arctanh cannot include the interval [-1,1]
- argument
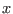 of
of 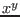 where
where 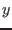 is not an integer should be positive
is not an integer should be positive
- argument
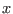 of
of 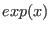 should not be too large to avoid
overflow problem.
should not be too large to avoid
overflow problem.
If you use your own evaluation procedure and are aware of evaluation problems and modify the returned values if such case occurs it will be a good policy to set C++ flags ALIAS_ChangeF, ALIAS_ChangeJ to 1 (default value 0) if a change occurs. Currently the interval Newton scheme that is embedded in some of the solving procedures of ALIAS will not be used if one of these flags is set to 1 during the calculation.
Dealing with infinity
In some specific cases we may have to deal with interval in which infinity is used. These quantities are represented using BIAS convention, BiasNegInf representing the negative infinity and BiasPosInf the positive infinity.
Non 0-dimensional system
Although the solving procedures of ALIAS are
mostly devoted to be used for 0 dimensional system
(i.e. systems having a finite number of solutions) most of them can
still be used for non 0-dimensional system. In that case the result
will be a set of boxes which will be an approximation of the
solution. When dealing with such system it is necessary to set the
global variable ALIAS_ND to 1 (its default value is 0) and to
define a name in the character string ALIAS_ND_File. The
solution boxes of the system will be stored in a file with the
given name.
The quality of the approximation may be estimated with the flags
ALIAS_Volume_In, ALIAS_Volume_Neglected that give
respectively the total volume of the solution boxes and the total
volume of the neglected boxes (i.e. the boxes for which the algorithm
has not been able to determine if they are or not a solution of the
system).
Note that there are special procedures for 1-dimensional system, see
chapter 9.
General purpose solving algorithm
This algorithm enable to determine approximately the solutions of a
system of ![]() equations and inequalities
in
equations and inequalities
in ![]() unknowns. Hence this method may be used to solve
a system
composed of
unknowns. Hence this method may be used to solve
a system
composed of ![]() equations
equations
![]() ,
, ![]() inequalities
inequalities
![]() and
and ![]() inequalities
inequalities
![]() .
.
Mathematical background
Principle
Let
![]() be the set of unknowns and
let
be the set of unknowns and
let
![]() be the set of
be the set of ![]() intervals in which you are searching the solutions
of the
intervals in which you are searching the solutions
of the ![]() equations
equations
![]() (for the sake of simplicity we don't consider
inequalities but the extension to inequalities is straightforward).
(for the sake of simplicity we don't consider
inequalities but the extension to inequalities is straightforward).
We will denote by ![]() the interval value of
the interval value of ![]() when this
function is evaluated for the box
when this
function is evaluated for the box
![]() of the unknowns while
of the unknowns while ![]() will denote the
will denote the
![]() -dimensional interval vector constituted of the
-dimensional interval vector constituted of the ![]() when the
unknowns have the interval value defined by the set
when the
unknowns have the interval value defined by the set ![]() .
.
The algorithm will use a list of boxes ![]() whose maximal size
whose maximal size ![]() is an
input of the program. This list is initialized with
is an
input of the program. This list is initialized with ![]() . The
number of
. The
number of ![]() currently in the list is
currently in the list is ![]() and therefore at the
start of the program
and therefore at the
start of the program ![]() . The algorithm will also use an accuracy on
the variable
. The algorithm will also use an accuracy on
the variable ![]() and on the functions
and on the functions ![]() . The norm of a
. The norm of a ![]() is defined as:
is defined as:
The norm of the interval vector
The algorithm uses an index
- if
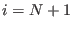 return
return 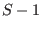 and
and 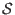 and exit
and exit
- bisect
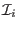 which produce
which produce 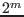 new interval vectors
new interval vectors
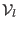 and set
and set 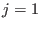
- for
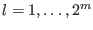
- evaluate
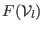
- if it exist
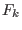 with
with 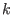 in
in ![$[1,n]$](img11.png) such that
such that
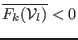 or
or
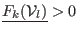 ,
then
,
then
 and go to step 3
and go to step 3
- if
 or
or
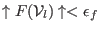 , then store
, then store 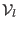 in
in 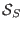 , increment
, increment 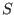 and go to step 3
and go to step 3
- store
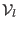 in
in 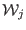 , increment
, increment  and go
to step 3
and go
to step 3
- evaluate
- if
 increment
increment 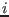 and go to step 1
and go to step 1
- if
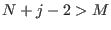 return a failure code as there is no space
available to store the new intervals
return a failure code as there is no space
available to store the new intervals
- if
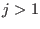 store one of the
store one of the  in
in 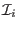 , the other
, the other
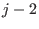 at the end of
at the end of 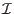 , starting at position
, starting at position 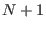 . Add
. Add 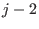 to
to 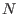 and go to step 1
and go to step 1
Now three problems have to be dealt with:
- how to choose the
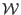 which will be put in place of the
which will be put in place of the
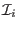 and in which order to store the other
and in which order to store the other  at the
end of the list?
at the
end of the list?
- can we improve the management of the bisection process in order
to conclude the algorithm with a limited number
 ?
?
- how do we distinguish distinct solutions ?
Managing the bisection and ordering
The second problem is solved in the following way: assume that at some
step of the algorithm the bisection process leads to the creation of
Now we have to manage the ordering of the ![]() . We have defined
two types of order for a given set of boxes
. We have defined
two types of order for a given set of boxes ![]() :
:
- maximum equation ordering: the box are ordered
along the value of
 for
all
for
all  in [1,
in [1,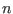 ]. The first box will have the lowest
]. The first box will have the lowest 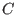 .
.
- maximum middle-point equation ordering: let
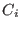 be the
vector whose components are the middle points of the intervals
be the
vector whose components are the middle points of the intervals 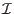 .
The box are ordered
along the value of
.
The box are ordered
along the value of
 for
all
for
all 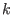 in [1,
in [1,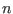 ]. The first box will have the lowest
]. The first box will have the lowest 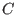 .
.
This method of managing the bisection is called the
Direct Storage mode and is the default mode in ALIAS. But
there is another mode, called the Reverse Storage
mode.
In
this mode we still substitute the ![]() by the
by the
![]() having the lowest
having the lowest ![]() but instead of adding the remaining
but instead of adding the remaining ![]()
![]() at the end of the list
at the end of the list ![]() we shift by
we shift by ![]() the
boxes in the list, thereby freeing the storage of
the
boxes in the list, thereby freeing the storage of
![]() which is used to store the remaining
which is used to store the remaining ![]()
![]() . In other words we may consider the solving procedure as
finding a leaves in a tree which are solutions of the problem: in the
Direct Storage mode we may jump during the bisection from one
branch of the tree to another while in the Reverse storage mode
we examine all the leaves issued from a branch of
the tree before examining the other branches of the tree. If we are
looking for all the solutions the storage mode has no influence on the
total number of boxes that will be examined. But the Reverse
Storage mode may have two advantages:
. In other words we may consider the solving procedure as
finding a leaves in a tree which are solutions of the problem: in the
Direct Storage mode we may jump during the bisection from one
branch of the tree to another while in the Reverse storage mode
we examine all the leaves issued from a branch of
the tree before examining the other branches of the tree. If we are
looking for all the solutions the storage mode has no influence on the
total number of boxes that will be examined. But the Reverse
Storage mode may have two advantages:
- if we are looking for only one solution it may enable to find it more rapidly (but that is not compulsory, see section 2.3.5.4),
- as we are following one branch at a time we will consider very rapidly small box that either will lead to a solution or will be discarded thereby enabling to free some storage space. Hence the storage space available in the reverse mode will be in general higher than in the direct mode: a practical consequence is that a problem may not be solved with the direct mode due to problem in the storage while with the same amount of storage solutions will be obtained in the reverse mode.
An alternative: the single bisection
A possibility to reduce the combinatorial explosion of the previous
algorithm is to bisect not all the variables i.e. to use the
full bisection mode, but only one of
them (it must be noted that the algorithms in ALIAS will not
accept a full bisection mode if the number of unknowns exceed
10). This may reduce the computation time as the number of function
evaluation may be reduced. But the problem is to determine which
variable should be bisected. All the solving algorithms of ALIAS
may manage this single bisection by setting the flag Single_Bisection to a value different from 0.
The value of this global variable indicates various bisection modes.
Although the behavior of the
mode may change according to the algorithm here are the
possible modes for the general solving algorithm and the corresponding
values for Single_Bisection:
- 1 : we just split the variable having the largest width (valid for all algorithms). Note however that it is still possible to order the bisection i.e. to split first a subset of the unknowns until their width is small (i.e. lower than ALIAS_Accuracy, then another subset and so on. This is obtained by setting flag ALIAS_Ordered_Bisection to 1 and defining an integer matrix ALIAS_Order_Bisection whose rows indicate the bisected subset and should end by 0. For example if this matrix has as rows [1,3,0],[2,4,5,0], then the algorithm will first bisect the unknowns 1 and 3 until their width is small, then the unknowns 2,4,5. If all unknowns indicated in the rows of the matrix have a small width, then the bisection algorithm revert to the normal behavior.
- 2: to determine the variable that will be bisected we use the following
approach: we compute the order criteria for the two boxes
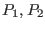 that will result from the bisection of variable
that will result from the bisection of variable 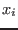 and retain the lowest
criteria
and retain the lowest
criteria 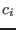 . The variable that will be bisected is the one that has the
lowest
. The variable that will be bisected is the one that has the
lowest 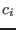 except if for at least one variable the interval
evaluation of the function for
except if for at least one variable the interval
evaluation of the function for 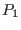 or
or 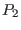 does not contain 0. In
that case the variable that will be bisected is the one that
verify the previous property and which has the lowest
does not contain 0. In
that case the variable that will be bisected is the one that
verify the previous property and which has the lowest 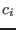 among all
the input intervals having the property.
However to avoid bisecting over and over
the same variable we use another test: let
among all
the input intervals having the property.
However to avoid bisecting over and over
the same variable we use another test: let 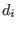 be the width of the
interval
be the width of the
interval
![$[\underline{x_i},\overline{x_i}]$](img118.png) and
and 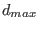 be the
maximum of all the
be the
maximum of all the 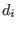 . If
. If
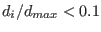 we don't consider the
variable
we don't consider the
variable 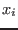 as a possible bisection direction.
It is also possible to mix this mode with mode 1. If the integer
variable ALIAS_RANDG is set to a strictly positive value then
ALIAS_RANDG bisection will be performed using mode 2 while the
next bisection will be performed using mode 1 and the process will be
repeated
as a possible bisection direction.
It is also possible to mix this mode with mode 1. If the integer
variable ALIAS_RANDG is set to a strictly positive value then
ALIAS_RANDG bisection will be performed using mode 2 while the
next bisection will be performed using mode 1 and the process will be
repeated
- 3, 4 : similar to 1
- 5 : we use a round-robin mode i.e. each variable is
bisected in turn (first
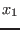 , then
, then 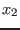 and so on) unless the width
of the input intervals is less than the desired accuracy on the
variable, in which case the bisected variable is the next one having a
sufficient width (valid for all algorithms)
The flag ALIAS_Round_Robin is used to indicate at each
bisection which variable should be bisected.
and so on) unless the width
of the input intervals is less than the desired accuracy on the
variable, in which case the bisected variable is the next one having a
sufficient width (valid for all algorithms)
The flag ALIAS_Round_Robin is used to indicate at each
bisection which variable should be bisected.
- 6: we emulate the smear function (see section 2.4.1.3) with an estimation of the gradient based on finite difference (procedure Select_Best_Direction_Grad)
- 7: here again we use the flag ALIAS_Ordered_Bisection set to 1 and defining an integer matrix ALIAS_Order_Bisection whose rows indicates an order for bisecting the unknowns. The largest variable in the first row will be bisected first and so on until all the variables in a row have a width lower than ALIAS_Accuracy. We then proceed to the second row. As soon as all variables in all rows have a width lower than ALIAS_Accuracy we use the bisection 1.
- 20: the user has defined its own bisection procedure, see section 11.3
There is another mode called the mixed bisection: among the ![]() variables we will bisect
variables we will bisect ![]() variables, which will lead to
variables, which will lead to
![]() new boxes. This mode is obtained by setting
the global integer variable
new boxes. This mode is obtained by setting
the global integer variable
ALIAS_Mixed_Bisection
to ![]() . Whatever is the value of
Single_Bisection we will order the variables according to their width
and select the
. Whatever is the value of
Single_Bisection we will order the variables according to their width
and select the ![]() variables having the largest width.
variables having the largest width.
Solutions and Distinct solutions
An interval will be considered as a solution for a function of the system in the following cases:
- for equations the maximal diameter of the intervals is less than a given threshold epsilon and the corresponding interval evaluation of the function contains 0 or the corresponding interval evaluation of the function has a diameter less than a given threshold epsilonf and the interval contains 0
- for inequalities
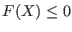 : the upper bound of
the interval evaluation of the
function is negative or the maximal diameter of the
intervals is less than
a given threshold epsilon and the corresponding interval
evaluation of the function has at least a negative lower bound or the corresponding interval
evaluation of the function has a diameter less than a given threshold
epsilonf and the interval contains 0
: the upper bound of
the interval evaluation of the
function is negative or the maximal diameter of the
intervals is less than
a given threshold epsilon and the corresponding interval
evaluation of the function has at least a negative lower bound or the corresponding interval
evaluation of the function has a diameter less than a given threshold
epsilonf and the interval contains 0
- for inequalities
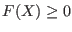 : the lower bound of
the interval evaluation of the
function is positive or the maximal diameter of the
intervals is less than
a given threshold epsilon and the corresponding interval
evaluation of the function has at least a positive upper bound or the corresponding interval
evaluation of the function has a diameter less than a given threshold
epsilonf and the interval contains 0
: the lower bound of
the interval evaluation of the
function is positive or the maximal diameter of the
intervals is less than
a given threshold epsilon and the corresponding interval
evaluation of the function has at least a positive upper bound or the corresponding interval
evaluation of the function has a diameter less than a given threshold
epsilonf and the interval contains 0
Assume that two solutions
![]() have been found
with the algorithm.
We will first consider the case where we have to solve a system of
have been found
with the algorithm.
We will first consider the case where we have to solve a system of ![]() equations in
equations in ![]() unknowns, possible with additional inequality
constraints.
First we will check with the Miranda theorem (see
section 3.1.5) if
unknowns, possible with additional inequality
constraints.
First we will check with the Miranda theorem (see
section 3.1.5) if
![]() include one (or
more) solution(s). If both solutions are Miranda, then they will kept
as solutions. If one of them is Miranda and other one is not Miranda
we will consider the distance between the mid-point of
include one (or
more) solution(s). If both solutions are Miranda, then they will kept
as solutions. If one of them is Miranda and other one is not Miranda
we will consider the distance between the mid-point of
![]() : if this distance is lower than a given threshold we will
keep as solution only the Miranda's one. If none of
: if this distance is lower than a given threshold we will
keep as solution only the Miranda's one. If none of
![]() is Miranda we keep these solutions, provided that their distance
is greater than the threshold. Note that in that case these solutions
may disappear if a Miranda solution is found later on such that the
distance between these solutions and the Miranda's one is lower than
the threshold.
is Miranda we keep these solutions, provided that their distance
is greater than the threshold. Note that in that case these solutions
may disappear if a Miranda solution is found later on such that the
distance between these solutions and the Miranda's one is lower than
the threshold.
In the other case the solution will be ranked according the chosen order and if a solution is at a distance from a solution with a better ranking lower than the threshold, then this solution will be discarded.
The 3B method
In addition to the classical bisection process all the solving algorithms in the ALIAS library may make use of another method called the 3B-consistency approach [2].
Although its principle is fairly simple
it is usually very efficient (but not always, see
section 2.4.3.1). In this method we consider each variable
![]() in turn and its range
in turn and its range
![]() . Let
. Let
![]() be the middle point of this range. We will first calculate the
interval evaluation of
the functions in the system with the full ranges for the variable
except for the variable
be the middle point of this range. We will first calculate the
interval evaluation of
the functions in the system with the full ranges for the variable
except for the variable ![]() where the range will be
where the range will be
![]() . Clearly if one of the equations is not
satisfied (i.e. its interval evaluation does not contain 0), then we
may reduce the range of the variable
. Clearly if one of the equations is not
satisfied (i.e. its interval evaluation does not contain 0), then we
may reduce the range of the variable ![]() to
to
![]() . If this is not the case we will define a new
. If this is not the case we will define a new
![]() as the middle point of the interval
as the middle point of the interval
![]() and repeat the process until either we have found an equation that is
not satisfied (in which case the interval for the variable
and repeat the process until either we have found an equation that is
not satisfied (in which case the interval for the variable ![]() will be
reduced to
will be
reduced to
![]() ) or the width of the interval
) or the width of the interval
![]() is lower than a given threshold
is lower than a given threshold ![]() . Using this
process we will reduce the range for the variable
. Using this
process we will reduce the range for the variable ![]() on the left side
and we may clearly use a similar procedure to reduce it on the left
side. The 3B procedure will be repeated if:
on the left side
and we may clearly use a similar procedure to reduce it on the left
side. The 3B procedure will be repeated if:
- the variable ALIAS_Full3B is set to 1 or 2 (default value: 0) and if there are two changes on the variable (a change is counted when a variable is changed either on the left or right side) or the change in at least one variable is larger than ALIAS_Full3B_Change
- the variable
ALIAS_Full3B
is set to 1 and the change in at least
one variable is larger than
ALIAS_Full3B_Change
For all the algorithms of ALIAS this method may be used by
setting the flag ALIAS_Use3B to 1 or 2. In addition you will have to
indicate for each variable a threshold ![]() and a maximal width for the
range (if the width of the range is greater than this maximal value
the method is not used). This is done through the VECTOR
variables ALIAS_Delta3B and ALIAS_Max3B. The difference
of behavior of the method if ALIAS_Use3B is set to 1 or 2 is
the following:
and a maximal width for the
range (if the width of the range is greater than this maximal value
the method is not used). This is done through the VECTOR
variables ALIAS_Delta3B and ALIAS_Max3B. The difference
of behavior of the method if ALIAS_Use3B is set to 1 or 2 is
the following:
- 1: let e be the value of ALIAS_Delta3B for the current variable which is in the range [a,b]. On the left side we will check if [a,a+e] may lead to no solution. If yes then the current value of the variable is [a+e,b]. We will start again but this time we will double the size of of the interval we will check i.e. we will test the elimination of [a+e,a+3e], then [a+3e,a+7e] and will stop as soon as the check on one interval fail. For example assume that the test for [a+3e,a+7e] fails, then the updated range for the variable will be [a+3e,b].
- 2: the procedure at the beginning is similar to the previous one but changes when the check fails. In the previous example after the failure for [a+3e,a+7e] we will start again to examine if interval with width e can be eliminated. Hence we will check [a+3e,a+4e], then [a+4e,a+6e] and so on. In consequence in this mode we will get as left bound for the interval the highest possible value A such that [A,A+e] cannot be eliminated. Clearly in that case the procedure will be more computer intensive but will produce better results.
ALIAS_Use3B=1;
Resize(ALIAS_Delta3B,25);Resize(ALIAS_Max3B,25);
for(i=1;i<=25;i++)
{
ALIAS_Delta3B(i)=0.1;ALIAS_Max3B(i)=7;
}
which indicate that we will start using the 3B method as soon as the
width of a range is lower than 7 and will stop it if we cannot improve
the range by less than 0.1.
A drawback of the 3B method is that it may imply a large number of
calls to the evaluation of the functions. The larger number of
evaluation will be obtained by setting the ALIAS_Use3B to 2 and
ALIAS_Full3B to 1 while the lowest number will be obtained if
these values are 1 and 0. It is possible to specify
that only a subset of the functions (the simplest)
will be checked in the process. This is done with the global variable
ALIAS_SubEq3B,
an integer array whose size should be set to the number of functions
and for which a value of 1 at position ![]() indicates that the function
indicates that the function
![]() will be used in the 3B process while a value of 0 indicates that
the function will not be used.
For example:
will be used in the 3B process while a value of 0 indicates that
the function will not be used.
For example:
Resize(ALIAS_SubEq3B,10); Clear(ALIAS_SubEq3B); ALIAS_SubEq3B(1)=1; ALIAS_SubEq3B(2)=1;indicates that only the two first functions will be used in the 3B process. If you are using your own solving procedure, then it is necessary to indicate that only part of the equations are used by setting the flag ALIAS_Use_SubEq3B to 1.
In some cases it may be interesting to try to use at least once the 3B method even if the width of the range is larger than ALIAS_Max3B. If the flag ALIAS_Always3B is set to 1, then the 3B will be used once to try to remove the left or right half interval of the variables.
If you are using also a simplification procedure (see section 2.3.3) you may avoid using this simplification procedure by setting the flag ALIAS_Use_Simp_In_3B to 0. You may also adapt the simplification procedure when it is called within the 3B method. For that purpose the flag ALIAS_Simp_3B is set to 1 instead of 0 when the simplification procedure is called within the 3B method. For some procedure if ALIAS_Use_Simp_In_3B is set to 2 then ALIAS_Simp_3B is set to 1 when the whole input is checked. But if ALIAS_Use_Simp_3B is set to a value larger than 2 then ALIAS_Simp_3B is set to 0.
Some methods allows to start the 3B method not by a small increment that is progressively increased but by a large increment (half the width of the interval) and to decrease it if it does not work. This is done by setting the flag ALIAS_Switch_3B to a value between 0 and 1: if the width of the current interval is lower than the width of the initial search domain multiplied by this flag, then a small increment is used otherwise a large increment is used.
When the routine that evaluate the expression uses the derivatives of the expression we may avoid to use these derivatives if the width of the ranges in the box are too large. This is obtained by assigning the size of the vector ALIAS_Func_Grad to the number of unknowns and assigning to the components of this vector to the maximal width for the ranges of the variables over which the derivatives will not be used: if there is a range with a width larger than its limits then no derivatives will be used.
Note also that the 3B-consistency is not the only one that can be used: see for example the ALIAS-Maple manual that implements another consistency test for equations which is called the 2B-consistency or Hull-consistency in the procedure HullConsistency (similarly HullIConsistency implement it for inequalities). See also the section 2.17 for an ALIAS-C++ implementation of the 2B and section 11.4 for detailed calls to the 3B procedures.
Simplification procedure
Most of the procedures in ALIAS will accept as optional last argument the name of a simplification procedure: a user-supplied procedure that take as input the current box and proceed to some further reduction of the width of the box or even determine that there is no solution for these box, in which case it should return -1. Such procedure must be implemented as:
int Simp_Proc(INTERVAL_VECTOR & P)where P is the current box. This procedure must return either -1 or any other integer. If a reduction of an interval is done within this procedure, then P must be updated accordingly.
This type of procedure allows the user to add information to the algorithm without having to add additional equations. The simplification procedure is applied on a box before the bisection and is used within the 3B method if this heuristic is applied.
Note that the Maple package associated to ALIAS allows in some cases to produce automatically the code for such procedure (see the ALIAS-Maple manual) and that section 2.17 presents a standard simplification procedure that may be used for almost any system of equations.
Implementation
The algorithm is implemented as:
int Solve_General_Interval(int m,int n,
INTEGER_VECTOR Type_Eq,
INTERVAL_VECTOR (* IntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_VECTOR & TheDomain,
int Order,int M,int Stop,
double epsilon,double epsilonf,double Dist,
INTERVAL_MATRIX & Solution,int Nb,
int (* Simp_Proc)(INTERVAL_VECTOR &))
the arguments being:
- m: number of unknowns
- n: number of functions, see the note 2.3.4.1
- Type_Eq: type of the functions, see the note 2.3.4.2
- IntervalFunction: a function which return the interval vector evaluation of the functions, see the note 2.3.4.3
- TheDomain: box in which we are looking for solution of the system. A copy of the search domain is available in the global variable ALIAS_Init_Domain
- Order: the type of order which is used to store the intervals created during the bisection process. This order may be either MAX_FUNCTION_ORDER or MAX_MIDDLE_FUNCTION_ORDER. See the note on the order 2.3.4.4.
- M: the maximum number of boxes which may be stored. See the note 2.3.4.5
- Stop: the possible values are 0,1,2
- 0: the algorithm will look for every solution in TheDomain
- 1: the algorithm will stop as soon as 1 solution has been found
- 2: the algorithm will stop as soon as Nb solutions have been found
- epsilon: the maximal width of the solution intervals, see the note 2.3.4.6
- epsilonf: the maximal width of the function intervals for a solution, see the note 2.3.4.6
- Dist: minimal distance between the middle point of two interval solutions, see the note 2.3.4.7
- Solution: an interval matrix of size (Nb,m) which will contained the solution intervals. This list is sorted using the order specified by Order
- Nb: the maximal number of solution which will be returned by the algorithm
- Simp_Proc: a user-supplied procedure that take as input the current box and proceed to some further reduction of the width of the box or even determine that there is no solution for this box, in which case it should return -1. Remember also that you may use the 3B method to improve the efficiency of this algorithm (see section 2.3.2).
Note that the following arguments may be omitted:
- Type_Eq: in that case all the functions will supposed to be equations.
- Simp_Proc: no simplification procedure is provided by the user
Number of unknowns and functions
The only constraint on n,m is that they should be strictly positive. So the algorithm is able to deal with under-constrained or over-constrained systems.
Type of the functions
The i-th value
in the array of - Type_Eq(i)=0 :
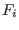 must verify
must verify 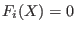
- Type_Eq(i)=1 :
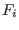 must verify
must verify 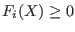
- Type_Eq(i)=-1 :
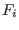 must verify
must verify 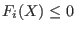
Interval Function
The user must provide a function which will compute the function intervals of the functions for a given box. When designing ALIAS we have determined that to be efficient we need a procedure that allow to calculate the interval evaluation of all the functions or only a subgroup of them in order to avoid unnecessary calculations. Hence the syntax of this procedure is:
INTERVAL_VECTOR IntervalFunction (int l1,int l2,INTERVAL_VECTOR & x)
- x: a
 dimensional interval vector which define the
intervals for the unknowns
dimensional interval vector which define the
intervals for the unknowns
- l1,l2: the function must be able to return the interval value of the functions l1 to l2. The first function has number 1, the last m. So if l1=l2=1 the function should return an interval vector whose only the first component has been computed.
The efficiency of the algorithm is heavily dependent on the way this procedure is written. Two factors are to be considered:
- efficiency of the evaluation
- sharp bound on the evaluation
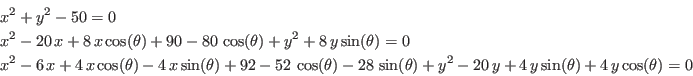
The evaluation function may be written as:
e1 = Sqr(x)+Sqr(y)-50.0 ;
e2 =Sqr(x)-20.0*x+8.0*x*Cos(teta)+90.0-80.0*Cos(teta)+Sqr(y)+8.0*y*Sin(teta);
e3 =Sqr(X)-6.0*x+4.0*x*Cos(teta)-4.0*x*Sin(teta)+92.0-52.0*Cos(teta)-28.0*
Sin(teta)+SQR(Y)-20.0*y+4.0*y*Sin(teta)+4.0*y*Cos(teta);
or, using temporary variables:
t1 = Sqr(x); t2 = Sqr(y); t5 = Cos(teta); t6 = x*t5; t9 = Sin(teta); t10 = y*t9; e1 = t1+t2-50.0; e2 = t1-20.0*x+8.0*t6+90.0-80.0*t5+t2+8.0*t10; e3 = t1-6.0*x+4.0*t6-4.0*x*t9+92.0-52.0*t5-28.0*t9+t2-20.0*y+4.0*t10+4.0*y*t5;the second manner is more efficient as the intervals
The second point is the sharpness of the evaluation. Let consider the
polynomial ![]() . If the variable lie in the interval [0,1] the
evaluation will lead to the interval [-1,1]. The same polynomial may
we written in Horner form
as
. If the variable lie in the interval [0,1] the
evaluation will lead to the interval [-1,1]. The same polynomial may
we written in Horner form
as ![]() the function being then evaluated as [-1,0].
Now suppose that
the function being then evaluated as [-1,0].
Now suppose that ![]() lie in [0.8,1.1]. The initial polynomial will be
evaluated as [-0.46,0.41] while in Horner form the evaluation leads to
[-0.22,0.11]. But this polynomial may also be written as
lie in [0.8,1.1]. The initial polynomial will be
evaluated as [-0.46,0.41] while in Horner form the evaluation leads to
[-0.22,0.11]. But this polynomial may also be written as ![]() (which is the centered form at 1)
whose evaluation leads to [-0.2,0.14] which has a sharper lower bound
than in the Horner form (note that Horner form is very efficient
for the evaluation of a polynomial but do not lead always to the sharpest
evaluation of the bounds on the polynomial although this is some time
mentioned in the literature). Unfortunately there is no known method which
enable to determine what is the best way to express a given function
in order to get the sharpest possible bounds. For complex expression
you may use the procedures MinimalCout or Code of
ALIAS-Maple that try to produce the less costly formulation of a given
expression.
(which is the centered form at 1)
whose evaluation leads to [-0.2,0.14] which has a sharper lower bound
than in the Horner form (note that Horner form is very efficient
for the evaluation of a polynomial but do not lead always to the sharpest
evaluation of the bounds on the polynomial although this is some time
mentioned in the literature). Unfortunately there is no known method which
enable to determine what is the best way to express a given function
in order to get the sharpest possible bounds. For complex expression
you may use the procedures MinimalCout or Code of
ALIAS-Maple that try to produce the less costly formulation of a given
expression.
Another problem is the cost of the tests which are necessary to determine if the interval evaluation of one of the function does not include 0. Indeed let us assume that we have 40 equations and 7 unknowns and that we are considering a box such that the function interval all contain 0. When testing the functions we may either evaluate all the functions with one procedure call (with the risk of performing useless evaluations e.g. if the interval evaluation of the first equations does not contain 0) or evaluate the functions one after the other (at a cost of 40 procedure calls but avoiding useless equation evaluations). The best way balances the cost of procedure calls compared to the cost of equation evaluations. By default we are evaluating all the functions in one step but by setting the variable Interval_Evaluate_Equation_Alone to 1 the program will evaluate the functions one after the other.
A last problem is the interval valuation of the equations. Indeed you may remember that some expression may not be evaluated for some ranges for the unknowns (see section 2.1.1.3). If such problem may occur a solution is to include into this procedure a test before each expression evaluation that verify if the expression is interval-valuable. If not two cases may occur:
- the expression will never be interval-valuated whatever is the value of one of the unknown in its range (e.g. the expression involves ArcSin(x) and the range for x is [-4,-3])
- the expression may be evaluated for some values of the unknowns in their range (e.g. the expression involves Sqrt(x) while the range for x is [-3,10])
The order
Basically the algorithm just bisect the box TestDomain until one of the criteria described in 2.3.4.6 is
satisfied. The boxes resulting from the bisection process
are stored in a list and the boxes in the list are treated
sequentially. If we are looking only for one solution of the equation
or for the first Nb solutions of a system (see the Stop
variable) it is
important to store the new boxes in the list in an order
which ensure that we will treat first the boxes having the
highest probability of containing a solution.
Two types of ordering may be used, see section 2.3.1.2,
indicated by the flag MAX_FUNCTION_ORDER or MAX_MIDDLE_FUNCTION_ORDER.
Note that if we are looking for all the solutions of the system the order has still an importance: although all the boxes of the list will be treated the order define how close solution intervals will be distinguished (see for example section 2.3.5.2).
Storage
The boxes generated by the bisection process are stored in an interval matrix:
Box_Solve_General_Interval(M,m)The algorithm try to manage the storage in order to solve the problem with the given number M. As seen in section 2.3.1.2 two storage modes are available, the Direct Storage and the Reverse Storage modes, which are obtained by setting the global variable Reverse_Storage to 0 (the default value) or at least to the number of unknowns plus 1. See also section 8.3 to use a mixed strategy between the direct and reverse mode.
For both modes the algorithm will first run until the bisection of the current box leads to a total number of boxes which exceed the allowed total number. It will then delete the boxes in the list which have been already bisected, thereby freeing some storage space (usually larger for the reverse mode than for the direct mode) and will start again.
If this is not sufficient the algorithm will consider each box in the list and determine if the bisection process applied on the box does create any new boxes otherwise the box is deleted from the list. Note that this procedure is computer intensive and constitute a "last ditch" effort to free some storage space. You can disable this feature by setting the integer variable Enable_Delete_Fast_Interval to 0. If the storage space freed by this method is not sufficient the algorithm will exit with a failure return.
If epsilonf=0, epsilon=![]() and
and ![]() is the largest
width of the intervals in TestDomain, then the number of boxes
that will be considered in the direct mode
is
is the largest
width of the intervals in TestDomain, then the number of boxes
that will be considered in the direct mode
is ![]() with, in the worst case:
with, in the worst case:
| (2.2) |
| (2.3) |
If the procedure has to be used more than once it is possible to speed up the computation by allocating the storage space before calling the procedure. Then you may indicate that the storage space has been allocated beforehand by indicating a negative value for M, the number of boxes being given by the absolute value of M.
Note also that the bisection process applied only to one variable may lead to a better estimation of the roots of the system if the algorithm stops when the accuracy required on the variable is reached: indeed, compared to the standard algorithm, one (or more) of the variable may have been individually split before reaching the step where a full bisection will lead to a solution (see the example in section 2.4.3.2).
Note also a specific use of ALIAS_RANDG: if this integer is not set to 0, then every ALIAS_RANDG iteration the algorithm will put the box having the largest width as current box, except if the number of boxes remaining to be processed is greater than half the total number of available boxes.
Accuracy
Two criterion are used to determine if a box possibly includes a solution of the system:
- the largest width of the components of the box is lower than epsilon and the functions intervals for this box all contain 0
- the largest width of the function intervals is lower than epsilonf and they contain all 0. You must be aware that this test is only used if there is no inequality in the system. In that case it is compulsory to have an epsilon not equal to 0 otherwise the procedure may lead to an infinite loop.
If we use only the second criteria the width of the solution intervals cannot be determined and the functions should be roughly normalized (see the example in section 15.1.3 for the importance of the conditioning).
Distinct solutions
Two solution intervals will be assumed to contain distinct solutions if the minimal distance between the middle point of all the intervals is greater than the threshold Dist.
Return code
The procedure will return an integer : number of solutions
: number of solutions
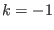 : the size of the storage is too low (
possible solutions: increase M,
or use the 3B method, or use the reverse storage mode or the single
bisection mode)
: the size of the storage is too low (
possible solutions: increase M,
or use the 3B method, or use the reverse storage mode or the single
bisection mode)
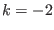 : m or n is not strictly positive
: m or n is not strictly positive
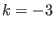 : Order is not 0 or 1
: Order is not 0 or 1
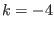 : one of the function in the system has not a type 0, -1
or 1 (i.e. it's not an equation, neither inequality
: one of the function in the system has not a type 0, -1
or 1 (i.e. it's not an equation, neither inequality 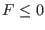 or an
inequality
or an
inequality 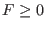 )
)
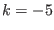 : we are in the optimization mode and more than one
functions are expressions to be optimized (see the Optimization chapter)
: we are in the optimization mode and more than one
functions are expressions to be optimized (see the Optimization chapter)
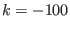 : in the mixed bisection mode the number of variables
that will be bisected is larger than the number of unknowns
: in the mixed bisection mode the number of variables
that will be bisected is larger than the number of unknowns
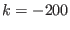 : one of the value of ALIAS_Delta3B or
ALIAS_Max3B is negative or 0
: one of the value of ALIAS_Delta3B or
ALIAS_Max3B is negative or 0
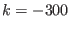 : one of the value of ALIAS_SubEq3B is not 0 or 1
: one of the value of ALIAS_SubEq3B is not 0 or 1
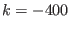 : although ALIAS_SubEq3B has as size the number of
equations none of its components is 1
: although ALIAS_SubEq3B has as size the number of
equations none of its components is 1
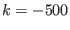 : ALIAS_ND is different from 0 (i.e. we are
dealing with a non-0 dimensional problem, see the corresponding
chapter) and the name of the result file has not been specified
: ALIAS_ND is different from 0 (i.e. we are
dealing with a non-0 dimensional problem, see the corresponding
chapter) and the name of the result file has not been specified
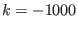 : the value of the flag Single_Bisection is not
correct
: the value of the flag Single_Bisection is not
correct
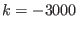 : we use the full bisection mode and the problem has
more than 10 unknowns
: we use the full bisection mode and the problem has
more than 10 unknowns
Debugging
If the algorithm fail some debugging options are provided. The
integer variable
Debug_Level_Solve_General_Interval indicate which level of debug is used:
- 0: no debug (the default value)
- 1: during the process are printed on the standard output: the index of the current box, the total number of boxes and the number of remaining boxes together with the current number of solutions
- 2 : same as 1 but the intervals of the current box are also printed and when it is split the new boxes are printed together with their function intervals
Examples and Troubleshooting
Example 1
We will present first a very silly example of system in the three
unknowns
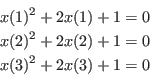
Clearly this system has the unique solution (-1,-1,-1). We choose to define the TestDomain as the interval [-2,0] for all three unknowns. So we define a function which specify the TestDomain:
VOID SetTestDomain (INTERVAL_VECTOR & x)
{
Resize (x, 3);
x(1) = Hull (-2.0,0.0);
x(2) = Hull (-2.0,0.0);
x(3) = Hull (-2.0,0.0);
}
The we have to define the IntervalFunction:
INTERVAL_VECTOR IntervalTestFunction (int l1,int l2,INTERVAL_VECTOR & x)
// interval valued functions. The input are intervals for the
//variables and the output is intervals on the functions
//x are the input variables and xx the function intervals
{
INTERVAL_VECTOR xx(3);
if(l1==1) xx(1)=x(1)*(x(1)+2)+1;
if(l1<=2 && l2>=2) xx(2)=x(2)*(x(2)+2)+1;
if(l2==3) xx(3)=x(3)*(x(3)+2)+1;
return xx;
}
This function returns the interval vector xx which will contain
the value of the function from l1 to l2 for the box
x. Note that the initial functions have been written
in Horner form (or "nested" form) which may lead to a sharper estimation of the
function intervals.
The main program may be written as:
INT main()
{
int Num; //number of solution
INTERVAL_MATRIX SolutionList(1,3);//the list of solutions
INTERVAL_VECTOR TestDomain;//the input intervals for the variable
//We set the value of the variable intervals
SetTestDomain (TestDomain);
//let's solve....
Num=Solve_General_Interval(3,3,IntervalTestFunction,TestDomain,
MAX_FUNCTION_ORDER,50000,1,0.001,0.0,0.1,SolutionList,1);
//too much intervals have been created, this is a failure
if(Num== -1)cout << "The procedure has failed (too many iterations)"<<endl;
return 0;
}
This main program will stop as soon as one solution has been found. We
set epsilonf to 0 and epsilon to 0.001 which mean that the
maximal width of the interval solution will be lower than 0.001. The
chosen order is the maximum equation ordering. The number of boxes
should not be larger than 50000 and the distance between the
distinct solutions must be greater than 0.1.
Running this program will provide the solution interval [-1.000977,-1] for all three variables and uses 71 boxes. The result will have been similar if we have chosen the maximum middle-point equation ordering.
On the other hand if we have epsilon to 0 and epsilonf to 0.001 the algorithm find the solution interval [-1.00048828125,-1] and use 78 boxes.
Now let's look at a more complete test program which enable to test the various options of the procedure.
INT main()
{
int Iterations;//maximal size of the storage
int Dimension,Dimension_Eq; // size of the system
int Num,i,j,order,precision,Stop;
// accuracy of the solution either on the function or on the variable
double Accuracy,Accuracy_Variable,Diff_Sol;
INTERVAL_MATRIX SolutionList(200,3);//the list of solutions
INTERVAL_VECTOR TestDomain;//the input intervals for the variable
INTERVAL_VECTOR F(3),P(3);
//We set the number of equations and unknowns and the value of the variable intervals
Dimension_Eq=Dimension=3;
SetTestDomain (TestDomain);
cerr << "Number of iteration = "; cin >> Iterations;
cerr << "Accuracy on Function = "; cin >> Accuracy;
cerr << "Accuracy on Variable = "; cin >> Accuracy_Variable;cerr << "Order (0,1)"; cin >>order;
cerr << "Stop at first solutions (0,1,2):";cin>>Stop_First_Sol;
cerr << "Separation between distincts solutions:";cin>> Diff_Sol;
//let's solve....
Num=Solve_General_Interval(Dimension,Dimension_Eq,IntervalTestFunction,TestDomain,order,Iterations,Stop,
Accuracy_Variable,Accuracy,Diff_Sol,SolutionList,1);
//too much intervals have been created, this is a failure
if(Num== -1){cout<<"Procedure has failed (too many iterations)"<<endl;return -1;}
cout << Num << " solution(s)" << endl;
for(i=1;i<=Num;i++)
{
cout << "solution " << i <<endl;
cout << "x(1)=" << SolutionList(i,1) << endl;
cout << "x(2)=" << SolutionList(i,2) << endl;
cout << "x(3)=" << SolutionList(i,3) << endl;
cout << "Function value at this point" <<endl;
for(j=1;j<=3;j++)F(j)=SolutionList(i,j);
cout << IntervalTestFunction(1,Dimension_Eq,F) <<endl;
cout << "Function value at middle interval" <<endl;
for(j=1;j<=3;j++)P(j)=Mid(SolutionList(i,j));
F=IntervalTestFunction(1,Dimension_Eq,P);
for(j=1;j<=3;j++)cout << Sup(F(j)) << endl;
}
return 0;
}
This program is basically similar to the previous one except that it
enable to define interactively the order, M, Stop, epsilon, epsilonf,Dist. Then it print the solution
together with the function interval for the solution interval and the
value of the functions at the middle point of the solution
interval. Let's test the algorithm to find all he solution (Stop=0) with epsilonf=0 and epsilon=0.001. The algorithm
will fail: indeed let's compute the maximal storage that we may need
using the formula (2.1). We end up with the number
Although academic this system shows several properties of interval analysis. If we set epsilon=epsilonf=1e-6, which is the standard setting of ALIAS-Maple, the algorithm will run for a very long time before finding the solution of the system. Even using the 3B method, section 2.3.2 and the 2B method (section 2.17) the computation time, although improved, will still be very large. Now if we write the system as
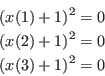
the system will be solved with only 8 boxes, with 2 boxes if we use the 3B method and without any bisection if we use the 2B method. This shows clearly the importance of writing the equations in the most compact form.
Example 2
The problem we want to solve is presented in section 15.1.1. We
consider a system of three equations in the unknowns ![]() :
:
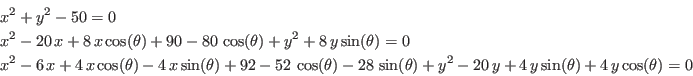
which admit the two solutions:
By looking at the geometry of the problem it is easy to establish a rough TestDomain:
VOID SetTestDomain (INTERVAL_VECTOR & x)
{
Resize (x, 3);
x(1) = Hull (0.9,7.1);
x(2) = Hull (2.1,7.1);
x(3) = Hull (-Constant::Pi,Constant::Pi);
}
and to determine that the maximum number of real solution is 6.
The IntervalFunction is written as:
INTERVAL_VECTOR IntervalTestFunction (int l1,int l2,INTERVAL_VECTOR & in)
{
INTERVAL_VECTOR xx(3);
if(l1==1)xx(1)=in(1)*in(1)+in(2)*in(2)-50.0;
if(l1<=2 && l2>=2)
xx(2)=-80.0*Cos(in(3))+90.0+(8.0*Sin(in(3))+in(2))*in(2)+(-20.0+8.0*Cos(in(3))+in(1))*in(1);
if(l2==3)
xx(3)=92.0-52.0*Cos(in(3))-28.0*Sin(in(3))+(-20.0+4.0*Sin(in(3))+
4.0*Cos(in(3))+in(2))*in(2)+(-4.0*Sin(in(3))-6.0+4.0*Cos(in(3))+in(1))*in(1);
return xx;
}
and we may use the same main program as in the previous example
(the name of this program is
Test_Solve_General1).
Let's assume that we set epsilonf to 0 and epsilon to 0.01 while looking at all the solutions (Stop=0), using the maximum equation ordering and setting Dist to 0.1. The algorithm provide the following solutions,using 684 boxes:
![\begin{eqnarray*}
&&x=[4.99297,4.99902] y=[5.00527,5.01016]
\theta=[-0.00...
...7031] y=[6.21133,6.21621]
\theta=[-0.809942,-0.803806]
\end{eqnarray*}](img172.png)
We notice that indeed none of the roots are contained in the solution intervals. If we use the maximum middle-point equation ordering the algorithm provide the solution intervals, using 684 boxes:
![\begin{eqnarray*}
&&x=[3.36426,3.37031] y=[6.21621,6.22109]
\theta=[-...
...508,5.01113] y=[4.99063,4.99551]
\theta=[0,0.00613592]
\end{eqnarray*}](img173.png)
which still does not contain the root (5,5,0) (but contain one of the root which show the importance of the ordering). Let's look at what is happening by setting the debug flag Debug_Level_Solve_General_Interval to 2 (see section 2.3.4.9). At some point of the process the algorithm has determined four different solution intervals:
![\begin{eqnarray*}
&& {\rm Solution 1}
[4.9990234375,5.005078125]
[4.990625...
...
[6.211328125,6.2162109375]
[-0.809941856,-0.803805932852]
\end{eqnarray*}](img174.png)
the criteria
Clearly solution 3 has the lowest criteria and will therefore be stored as the first solution. Then solution 1 will be considered: but the distance between the middle point of solution 3 and 1 is lower than Dist and therefore solution 1 will not be retained. The solution 2 will be considered but for the same reason than for solution 1 this solution will not been retained. Finally solution 4 will be considered and it spite of his index being the worse this solution will be retained as its distance to solution 3 is greater than Dist.
Note that if the single bisection is activated and setting the flag Single_Bisection to 1 we find the two roots for epsilonf to 0 and epsilon to 0.01 with 650 boxes using the maximum equation ordering.
We may also illustrate on this example how to deal
with
inequalities. Assume now that we want to deal with the same system but
also with the inequality ![]() . We modify the
IntervalTestFunction as:
. We modify the
IntervalTestFunction as:
INTERVAL_VECTOR IntervalTestFunction (int l1,int l2,INTERVAL_VECTOR & in)
{
INTERVAL x,y,teta;
INTERVAL_VECTOR xx(4);
x=in(1);y=in(2);teta=in(3);
if(l1==1)xx(1)=x*x+y*y-50.0;
if(l1<=2 && l2>=2)
xx(2)=-80.0*Cos(teta)+90.0+(8.0*Sin(teta)+y)*y+(-20.0+8.0*Cos(teta)+x)*x;
if(l1<=3 && l2>=3)
xx(3)=92.0-52.0*Cos(teta)-28.0*Sin(teta)+(-20.0+4.0*Sin(teta)+
4.0*Cos(teta)+y)*y+(-4.0*Sin(teta)-6.0+4.0*Cos(teta)+x)*x;
if(l2==4)
xx(4)=x*y-22.;
return xx;
}
Part of the main program will be:
Type(1)=0;Type(2)=0;Type(3)=0;Type(4)=-1; Num=Solve_General_Interval(3,4,Type,IntervalTestFunction,TestDomain,order, Iterations,Stop_First_Sol,Accuracy_Variable, Accuracy,Diff_Sol,SolutionList,6);Here Type(4)=-1; indicates that the fourth function is an inequality of the type
Example 3
This example is derived from example 2. We notice that in the three
functions of example 2 the second degree terms of
INTERVAL_VECTOR IntervalTestFunction (int l1,int l2,INTERVAL_VECTOR & in)
{
INTERVAL_VECTOR xx(1);
xx(1)=11092.0+(-25912.0+(19660.0-4840.0*Cos(in(1)))*Cos(in(1)))*Cos(in(1))+(
-508.0+(3788.0-1600.0*Cos(in(1)))*Cos(in(1)))*Sin(in(1));
return xx;
}
This program is implemented under the name
Test_Solve_General2.
With epsilonf=0 and epsilon=0.001
we get the solution
intervals, using 32 boxes:
for whatever order. If we use epsilon=0 and epsilonf=0.1 we get, using 50 boxes:
![\begin{eqnarray*}
&& \theta=[-0.806784012741056,-0.806781016684830]\\
&& \theta=[-4.793689962142628e-05,0]
\end{eqnarray*}](img182.png)
In both cases the solution intervals contain the roots of the equation.
Example 4
In this example (see section 15.1.3) we deal with a complex problem
of three equations in three unknowns
The system has a solution which is approximately:
This problem is extremely ill conditioned as for the TestDomain
the functions intervals are:
This program is implemented under the name Test_Solve_General. With espsilonf=0 and epsilon=0.001 and if we stop at the first solution we find with the maximum equation ordering:
with 531 boxes. We may also mention the following remarks:
- we get no improvement with the single bisection mode as we need 2435 boxes to find the first solution,
- using the Reverse Storage mode does not lead to any improvement for finding the first root: in this mode we need 5587 boxes to get the first solution,
with 203 boxes. The importance of normalizing the functions appears if we use epsilonf=0.1 and epsilon=0. If we stop at the first solution we find:
![\begin{eqnarray*}
&&\psi=[4.661660388259656,4.661660388340929]\\
&&\theta=[1.70...
...00898180284073]\\
&&\phi=[0.869388881899751,0.869388881940387]
\end{eqnarray*}](img189.png)
while if we divide the first function by 1000 we find:
![\begin{eqnarray*}
&&\psi=[4.661658091884636,4.661658424779772]\\
&&\theta=[1.70...
...00898570395561]\\
&&\phi=[0.869388105618527,0.869388272066095]
\end{eqnarray*}](img190.png)
in four time less computation time.
General comments
The advantages of the proposed algorithm is that it is easy to use and implement for a fast check. For sharp system it may provide quickly solutions with a reasonable accuracy. The drawback is that it may provide solutions intervals which does not contain roots or, worse, miss some roots if Dist is not set to 0 (see section 2.3.5.2).
This algorithm may be used also for analysis: if we have to solve numerous systems we may use this algorithm with a low M in order to fast check if the current system may have some real roots, in which case we may consider using a more sophisticated algorithm.
General purpose solving algorithm with Jacobian
Mathematical background
Assume now that we are able to compute the jacobian matrix of the system of functions. We will use this jacobian for improving the evaluation of the function intervals using two approaches:
- use the monotonicity of the function
- use the gradient for the evaluation of the function intervals
A notable difference with the previous procedure is that we use Moore theorem (see section 3.1.1) to determine if a unique solution exists in a given box, in which case we use Krawczyk method for determining this solution (see section 2.10). Therefore if the algorithm proposes as solution a point instead of a range this imply that this solution has been obtained as the result of Moore theorem. Note however that getting a range for a solution instead of a point does not always imply that we have a singular solution. For example it may happen that the solution is exactly at one extremity of a box (see example in section 2.4.3.2) which a case that our algorithm does not handle very well. A local analysis of the solution should however confirm quickly if the solution is indeed singular.
In addition we use also the inflation method presented in section 3.1.6 to increase the width of the box in which we may guarantee that there is a unique solution.
Hence this algorithm allows to determine exact solutions in the sense that we determine boxes that contains a unique solution and provides a guaranteed numerical scheme that allows for the calculation of the solution.
In the same way we use the Hansen-Sengupta version of the interval Newton method to improve the boxes (see [21]). Note that an improved interval Newton that may benefit from the structure of the system is available (see section 3.1.4).
This algorithms allows also to determines the solutions of non-0 dimensional system, see section 2.2.
Using the monotonicity
For a given box we will compute the jacobian matrix using
interval analysis. Each row ![]() of this interval matrix enable to get some
information of the corresponding function
of this interval matrix enable to get some
information of the corresponding function ![]() .
.
- if the i-th column of the j-th row is an interval which is
strictly negative or strictly positive, then
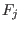 is monotonic with
respect to the unknowns
is monotonic with
respect to the unknowns 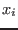
- if the i-th column of the j-th row is equal to 0, then function
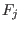 does not depend on the variable
does not depend on the variable 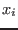
The algorithm for computing a sharper evaluation of ![]() is:
is:
![]() =Evaluate
=Evaluate![]() (
(
![]() )
)
- compute
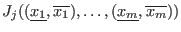
- let
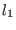 be the number of components of
be the number of components of  such that
such that
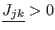 or
or
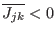 and let
and let
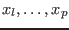 be the variables for which this occur
be the variables for which this occur
- if
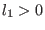
loop: for all combination of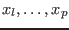 in the set
in the set
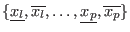 :
:
- if
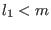
- compute
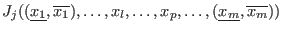
- let
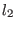 be the number of components of
be the number of components of 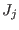 such that
such that
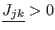 or
or
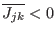
- if
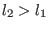 , then
, then
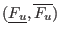 =Evaluate
=Evaluate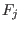 (
(
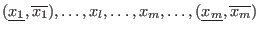 )
)
- otherwise
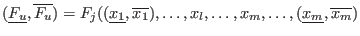 )
)
- if this is the first estimation of
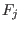 then
then 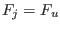
- otherwise
- if
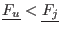 , then
, then
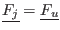
- if
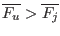 , then
, then
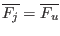
- if
- compute
- otherwise
-
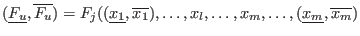 )
)
- if this is the first estimation of
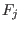 then
then 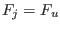
- otherwise
- if
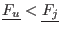 , then
, then
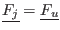
- if
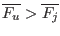 , then
, then
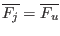
- if
-
- if
- end loop:
- otherwise
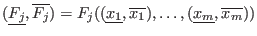
- return
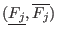
Improving the evaluation using the Jacobian and centered form
Let ![]() be the middle point of
be the middle point of
![]() and
and
![]() be the box. Then:
be the box. Then:
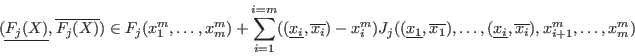 |
(2.4) |
This evaluation is embedded into the evaluation procedure of the solving algorithms using the Jacobian. It is also available in its general form as
INTERVAL_VECTOR Centered_Form(int DimVar,int DimEq,
INTERVAL_VECTOR (* TheIntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Gradient)(int, int, INTERVAL_VECTOR &),
VECTOR &Center,
INTERVAL_VECTOR &Input)
where
- DimVar: number of variables
- DimEq: number of expressions
- TheIntervalFunction: procedure in MakeF format for interval evaluating the expressions
- Gradient: procedure in MakeJ format for evaluating the derivatives of the expressions
- Center:the center point for the centered form
- Input: the ranges for the variables
INTERVAL Centered_Form(int k,int DimVar,int DimEq,
INTERVAL_VECTOR (* TheIntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Gradient)(int, int, INTERVAL_VECTOR &),
VECTOR &Center,
INTERVAL_VECTOR &Input)
which is used to evaluate only expression number
A more sophisticated evaluation for the centered form is based on
Baumann theorem [18]. First we define the procedure
cut(double x,INTERVAL X) as:
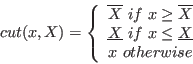
For a system of
For a given equation
with
INTERVAL_VECTOR BiCentered_Form(int DimVar,
int DimEq,
INTERVAL_VECTOR (* TheIntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Gradient)(int, int, INTERVAL_VECTOR &),
INTERVAL_VECTOR &Input,
int Exact)
where
- DimVar: number of variables
- DimEq: number of expressions
- TheIntervalFunction: procedure in MakeF format for interval evaluating the expressions
- Gradient: procedure in MakeJ format for evaluating the derivatives of the expressions
- Input: the ranges for the variables
- Exact: if 0 the procedure will return as soon as an interval evaluation of one expression does not include 0
INTERVAL_VECTOR BiCentered_Form(int k,int DimVar,
int DimEq,
INTERVAL_VECTOR (* TheIntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Gradient)(int, int, INTERVAL_VECTOR &),
INTERVAL_VECTOR &Input,
int Exact)
Another variant is based on the property that the numerical interval evaluation of the product J(Input)(Input-Center) may be overestimated as there may be several occurence of the same variable in this product. We may assume that this product has been computed symbolically, then re-arranged to reduce the number of occurence of the same variable leading to a procedure in MakeF format that computes directly the product. The syntax of the bicentered form procedure is
INTERVAL_VECTOR BiCentered_Form(int DimVar,
int DimEq,
INTERVAL_VECTOR (* TheIntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Gradient)(int, int, INTERVAL_VECTOR &),
INTERVAL_VECTOR (* ProdGradient)(int, int, INTERVAL_VECTOR &),
INTERVAL_VECTOR &Input,
int Exact)
where ProdGradient is the procedure that computes the product
J(Input)(Input-Center), being understood that the Center
is available in the global variable
ALIAS_Center_CenteredForm.
Single bisection mode
We may use the single bisection mode i.e. bisect only one variable at a time. Fives modes exist for determining the variable to be bisected, the choice being made by setting Single_Bisection to a value from 1 to 8
- 1 : we just split the variable having the largest width
- 2 : this mode is based on the smear function
as defined by
Kearfott [7]: let
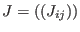 be the Jacobian
matrix of the system and let define for the variable
be the Jacobian
matrix of the system and let define for the variable 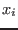 the
smear value
the
smear value
![$s_i = {\rm Max}(
\vert\underline{J_{ij}[\underline{x_i},\overline{x_i}]}\vert,
\vert\overline{J_{ij}[\underline{x_i},\overline{x_i}]}\vert$](img240.png)
![$\forall j\in
[1,n]$](img241.png) where
where 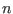 is the total number of functions. The variable that
will be bisected will be the one having the largest
is the total number of functions. The variable that
will be bisected will be the one having the largest 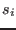 .
There is however a drawback f the smear function: let consider for
example the equation
.
There is however a drawback f the smear function: let consider for
example the equation 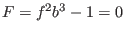 where
where 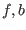 are large identical
intervals centered at 0.
The derivative of
are large identical
intervals centered at 0.
The derivative of 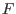 with respect to
with respect to 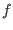 is
is 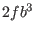 and
with respect to
and
with respect to 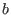
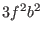 : multiplied by the width of the interval
we get
: multiplied by the width of the interval
we get 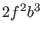 and
and 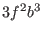 . Hence the smear function for
. Hence the smear function for 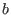 will
be in general larger than for
will
be in general larger than for 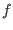 and
and 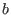 will always be bisected until its
width is lower than the desired accuracy. Another example in which the
smear function is not the best choice is presented in
section 2.4.3.4.
However the smear function is very often the most efficient mode and
should be privileged.
will always be bisected until its
width is lower than the desired accuracy. Another example in which the
smear function is not the best choice is presented in
section 2.4.3.4.
However the smear function is very often the most efficient mode and
should be privileged.
- 3 : this is similar to the smear function except that we take into account its drawback. To avoid bisecting over and over the same variable we impose that a variable may be considered for bisection only if the ratio of its width over the maximal width of the box is not lower than the variable ALIAS_Bound_Smear (default value 1.e-5).
- 4 : this mode is based on the Krawczyk operator:
to determine which variable should be bisected we
consider the box
![$P=\{[\underline{x_1},\overline{x_1}],\ldots,
[\underline{x_n},\overline{x_n}]\}$](img250.png) . When dealing with the variable
. When dealing with the variable
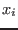 the single bisection mode will lead to two new boxes
the single bisection mode will lead to two new boxes
 . Let
. Let 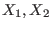 be the middle point of these boxes
We have seen (section 2.10) that a fundamental point
of Moore test
for determining the unicity of a solution in a box is
that
be the middle point of these boxes
We have seen (section 2.10) that a fundamental point
of Moore test
for determining the unicity of a solution in a box is
that
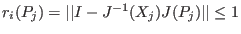 . Thus we will consider in turn
each of the variable and compute the value of
. Thus we will consider in turn
each of the variable and compute the value of  for both
for both  . The bisected variable will be chosen as the one leading to the
minimal value of all
. The bisected variable will be chosen as the one leading to the
minimal value of all 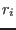 . However to avoid bisecting over and over
the same variable we use another test: let
. However to avoid bisecting over and over
the same variable we use another test: let 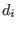 be the width of the
interval
be the width of the
interval
![$[\underline{x_i},\overline{x_i}]$](img118.png) and
and 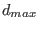 be the
maximum of all the
be the
maximum of all the 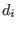 . If
. If
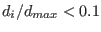 we don't consider the
variable
we don't consider the
variable 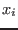 as a possible bisection direction.
as a possible bisection direction.
- 5: we use a round-robin mode i.e. each variable is
bisected in turn (first
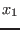 , then
, then 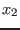 and so on) unless the width
of the range for the variable is less than the desired accuracy on the
variable, in which case the bisected variable is the next one having a
sufficient width
and so on) unless the width
of the range for the variable is less than the desired accuracy on the
variable, in which case the bisected variable is the next one having a
sufficient width
- 6: like mode 2 of SolveGeneral. ALIAS_RANDG may still be used to switch between mode 1 and mode 2 of SolveGeneral
- 7: like mode 2 of SolveGeneral except that it is assumed that the user has defined a simplification procedure that may allow to reduce the box directly within the bisection process
- 8: the variable are regrouped by groups of ALIAS_Tranche_Bisection elements. The bisection will look at each group in turn and bisect the first group that has elements whose diameter is larger than ALIAS_Size_Tranche_Bisection. When the element of the group have all elements whose diameter is lower than this threshold the bisection will consider the next group. If all elements of all groups have a diameter lower than the threshold the smear function will be used to determine which variable will be bisected.
The smear mode leads in general to better result
than the other modes (but there are exception, see example in
section 2.4.3.4).
There is another mode called the mixed bisection: among the ![]() variables we will bisect
variables we will bisect ![]() variables, which will lead to
variables, which will lead to
![]() new boxes. This mode is obtained by setting
the global integer variable
ALIAS_Mixed_Bisection
to
new boxes. This mode is obtained by setting
the global integer variable
ALIAS_Mixed_Bisection
to ![]() . Here we will order the variables according to the value of
their smear function (if the flag Single_Bisection is 2 or 3) or according to their width (for 1,4,5).
. Here we will order the variables according to the value of
their smear function (if the flag Single_Bisection is 2 or 3) or according to their width (for 1,4,5).
Implementation
The algorithm is implemented in generic form as:
int Solve_General_Gradient_Interval(int m,int n,
INTEGER_VECTOR Type_Eq,
INTERVAL_VECTOR (* IntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* IntervalGradient)(int, int, INTERVAL_VECTOR &),
INTERVAL_VECTOR & TheDomain,
int Order,int M,int Stop,
double epsilon,double epsilonf,double Dist,
INTERVAL_MATRIX & Solution,int Nb,INTEGER_MATRIX &GI,
int (* Simp_Proc)(INTERVAL_VECTOR &))
the arguments being:
- m: number of unknowns
- n: number of functions, see the note 2.3.4.1
- Type_Eq: type of the functions, see the note 2.3.4.2
- IntervalFunction: a function which return the interval vector evaluation of the functions, see the note 2.3.4.3. Remember that if you have equations and inequalities in the system you must first define the equations and then the inequalities.
- IntervalGradient: a function which the interval matrix of the jacobian of the functions, see the note 2.4.2.2
- TheDomain: box in which we are looking for solution of the system. A copy of the search domain is available in the global variable ALIAS_Init_Domain
- Order: the type of order which is used to store the boxes created during the bisection process. This order may be either MAX_FUNCTION_ORDER or MAX_MIDDLE_FUNCTION_ORDER. See the note on the order 2.3.4.4.
- M: the maximum number of boxes which may be stored. See the note 2.3.4.5
- Stop: the possible values are 0,1,2
- 0: the algorithm will look for every solution in TheDomain
- 1: the algorithm will stop as soon as 1 solution has been found
- 2: the algorithm will stop as soon as Nb solutions have been found
- epsilon: the maximal width of the box, see the note 2.3.4.6
- epsilonf: the maximal width of the function intervals, see the note 2.3.4.6. Note that if this value is set to 0, then Moore test is not used.
- Dist: minimal distance between the middle point of two interval solutions, see the note 2.3.4.7
- Solution: an interval matrix of size (Nb,m) which will contained the solution intervals. This list is sorted using the order specified by Order
- Nb: the maximal number of solution which will be returned by the algorithm
- GI: an integer matrix called the simplified
jacobian, which give a-priori information on
the sign of the derivative of the function. GI(i,j) indicates
the sign of the derivative of function i with respect to
variable j using the following code:
- -1: the derivative is always negative
- 0: the function is not dependent of variable j
- 1: the derivative is always positive
- 2: the sign of the derivative is not known
- Simp_Proc: a user-supplied procedure that take as input the current box and proceed to some further reduction of the width of the box components or even determine that there is no solution for this box, in which case it should return -1 (see note 2.3.3). Remember that you may use the 3B method to improve the efficiency of this algorithm (see section 2.3.2).
- Type_Eq: in that case all the functions will supposed to be equations.
- GI: in that case all the sign of the derivatives will supposed to be unknown
- Simp_Proc: no simplification procedure is provided by the user
Return code
The procedure will return an integer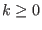 : number of solutions
: number of solutions
 : the size of the storage is too low (
possible solutions: increase M,
or use the 3B method, or use the reverse storage mode or the single
bisection mode)
: the size of the storage is too low (
possible solutions: increase M,
or use the 3B method, or use the reverse storage mode or the single
bisection mode)
 : m or n is not strictly positive
: m or n is not strictly positive
 : Order is not 0 or 1
: Order is not 0 or 1
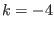 : one of the function in the system has not a type 0, -1
or 1 (i.e. it's not an equation, an inequality
: one of the function in the system has not a type 0, -1
or 1 (i.e. it's not an equation, an inequality 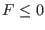 or an
inequality
or an
inequality 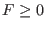 )
)
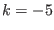 : we are in the optimization mode and more than one
functions are expressions to be optimized (see the Optimization chapter)
: we are in the optimization mode and more than one
functions are expressions to be optimized (see the Optimization chapter)
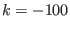 : in the mixed bisection mode the number of variables
that will be bisected is larger than the number of unknowns
: in the mixed bisection mode the number of variables
that will be bisected is larger than the number of unknowns
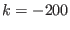 : one of the value of ALIAS_Delta3B or
ALIAS_Max3B is negative or 0
: one of the value of ALIAS_Delta3B or
ALIAS_Max3B is negative or 0
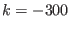 : one of the value of ALIAS_SubEq3B is not 0 or 1
: one of the value of ALIAS_SubEq3B is not 0 or 1
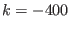 : although ALIAS_SubEq3B has as size the number of
equations none of its components is 1
: although ALIAS_SubEq3B has as size the number of
equations none of its components is 1
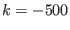 : ALIAS_ND is different from 0 (i.e. we are
dealing with a non-0 dimensional problem, see the corresponding
chapter) and the name of the result file has not been specified
: ALIAS_ND is different from 0 (i.e. we are
dealing with a non-0 dimensional problem, see the corresponding
chapter) and the name of the result file has not been specified
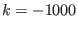 : the value of the flag Single_Bisection is not
correct
: the value of the flag Single_Bisection is not
correct
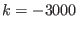 : we use the full bisection mode and the problem has
more than 10 unknowns
: we use the full bisection mode and the problem has
more than 10 unknowns
- ALIAS_Store_Gradient: if not 0 the gradient matrix of each box will be stored together with the input intervals. Must be set to 0 for large problem (default value: 1)
- ALIAS_Diam_Max_Gradient: if the maximal width of the ranges in a box is lower than this value, then the gradient will be used to perform the interval evaluation of the functions (default value: 1.e10)
- ALIAS_Diam_Max_Kraw: if the maximal width of the ranges in a box is lower than this value, then the Krawczyk operator will be used to determine if there is a unique solution in the box (default value: 1.e10)
- ALIAS_Diam_Max_Newton: if the maximal width of the ranges in a box is lower than this value, then the interval Newton method will be used either to try to reduce the width of the box or to to ensure that there is no solution of the system in the box (default value: 1.e10)
Jacobian matrix
The user must provide a function which will compute the interval
evaluation of the jacobian matrix
of its particular functions for a given box. As for the function
evaluation procedure we have chosen a syntax which shows the best
compromise between program calls and interval calculation.
The syntax of this function is:
INTERVAL_MATRIX IntervalGradient (int l1,int l2,INTERVAL_VECTOR & x)
- x: a
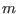 dimensional interval vector which define the
intervals for the unknowns
dimensional interval vector which define the
intervals for the unknowns
- l1,l2: the function must be able to return the interval evaluation of the component of the jacobian matrix at row l1 and column l2 i.e. the derivative of the function number l1 with respect to the variable number l2. The first row has number 1, the last n and the first column has number 1, the last m.
Note that if ALIAS_Store_Gradient has not been set to 0 we will store the simplified Jacobian matrix for each box. Indeed if for a given box B the interval evaluation of one element of the gradient has a constant sign (indicating a monotonic behavior of the function) setting the simplified jacobian matrix element to -1 or 1 allows to avoid unnecessary evaluation of the element of the Jacobian for the box resulting from a bisection of B as they will exhibit the same monotonic behavior. Although this idea may sound quite simple it has a very positive effect on the computation time. The name of the storage variable of the simplified jacobian is:
INTEGER_MATRIX Gradient_Solve_General_Interval
If a function ![]() is not differentiable you just set the value
of grad(i,..) to the interval [-1e30,1e30]. It is important to
define here a large
interval as the program Compute_Interval_Function_Gradient
that computes the interval evaluation of the function by using their
derivatives uses also the Taylor evaluation based on the value of the
derivatives: a small interval value of the derivatives may lead to a
wrong function evaluation.
is not differentiable you just set the value
of grad(i,..) to the interval [-1e30,1e30]. It is important to
define here a large
interval as the program Compute_Interval_Function_Gradient
that computes the interval evaluation of the function by using their
derivatives uses also the Taylor evaluation based on the value of the
derivatives: a small interval value of the derivatives may lead to a
wrong function evaluation.
Note also that a convenient way to write the Gradient
procedure is to use the procedure MakeJ offered by ALIAS-Maple
(see the ALIAS-Maple manual).
Take care also of the interval valuation
problems of
the element of the Jacobian (see section 2.1.1.3) which may
be different from the one of the functions: for example if a
function is
![]() it is interval-valuable as soon as the
lower bound of
it is interval-valuable as soon as the
lower bound of ![]() is greater or equal to 0 although the gradient will
involve
is greater or equal to 0 although the gradient will
involve ![]() which is not interval-valuable if the lower bound of
which is not interval-valuable if the lower bound of ![]() is equal to 0. ALIAS-Maple offers also the possibility to treat
automatically the interval-valuation problems of the jacobian elements.
is equal to 0. ALIAS-Maple offers also the possibility to treat
automatically the interval-valuation problems of the jacobian elements.
Evaluation procedure using the Jacobian
A better evaluation of the function intervals than the IntervalFunction can be obtained using the Jacobian matrix. A specific procedure can be used to obtain this evaluation:
INTERVAL_VECTOR Compute_Interval_Function_Gradient(int m,int n,
INTEGER_VECTOR &Type_Eq,
INTERVAL_VECTOR (* IntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* IntervalGradient)(int, int, INTERVAL_VECTOR &),
INTERVAL_VECTOR & Input, int Exact,
INTEGER_VECTOR &AG,INTEGER_MATRIX &AR)
This procedure computes the function intervals for the box
Input.
- Type_Eq is an integer array whose Dimension_Eq elements
indicates the nature of the functions: -1 for inequality
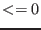 , 0 for
equation, 1 for inequality
, 0 for
equation, 1 for inequality 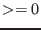 , -2 for a function to be minimized, 2
for a function to be maximized and 10 for a function to be both
minimized and maximized (note that for an optimization problem the
function that has to be minimized must be the last function in the
list of function).
, -2 for a function to be minimized, 2
for a function to be maximized and 10 for a function to be both
minimized and maximized (note that for an optimization problem the
function that has to be minimized must be the last function in the
list of function).
- the integer Exact should be put to 1 as for a value of 0 the procedure stop the evaluation of each box as soon as the lower bound of the interval is negative and the upper bound positive.
- AG is an integer vector of size m x n which indicates if the sign of some derivatives are already known (the elements should then have the values -1, 0 or 1) or not (the value must then be 2)
- AR is a return matrix with the sign of the derivatives for Input
- by taking into account of the monotonicity of the functions
- by using an interval evaluation of the functions based on their Taylor expansion: it is therefore necessary to evaluate rightly the derivatives of the functions
The best evaluation of the l-th equation may be computed with
INTERVAL Compute_Interval_Function_Gradient_Line(int l,int Dim_Var, int Dimension_Eq, INTERVAL_VECTOR (* IntervalFunction)(int,int,INTERVAL_VECTOR &), INTERVAL_MATRIX (* Gradient)(int, int, INTERVAL_VECTOR &), INTERVAL_VECTOR &Input,int Exact,INTEGER_VECTOR &AG)
Storage
The boxes generated by the bisection process are stored in an interval matrix:
Box_Solve_General_Interval(M,m)while the corresponding simplified Jacobian matrix is stored in the integer matrix of size (M, m
Gradient_Solve_General_Intervalcalled the simplified jacobian: the entry
The algorithm try to manage the storage in order to solve the problem with the given number M. As seen in section 2.3.1.2 two storage modes are available, the Direct Storage and the Reverse Storage modes, which are obtained by setting the global variable Reverse_Storage to 0 (the default value) or 1.
For both modes the algorithm will first run until the bisection of the current box leads to a total number of boxes which exceed the allowed total number. It will then delete the boxes in the list which have been already bisected, thereby freeing some storage space (usually larger for the reverse mode than for the direct mode) and will start again.
Examples
Example 1
This problem has been presented in section 2.3.5.1.
The IntervalGradient function is defined as:
INTERVAL_MATRIX IntervalGradient (int l1,int l2,INTERVAL_VECTOR & x)
{
INTERVAL_MATRIX Grad(3,3);
if(l1==1)
{
if(l2==1){Grad(1,1)=2*x(1)+2;return Grad;}
if(l2==2){Grad(1,2)=0;return Grad;}
if(l2==3){Grad(1,3)=0;return Grad;}
}
if(l1==2)
{
if(l2==1){Grad(2,1)=0;return Grad;}
if(l2==2){Grad(2,2)=2*x(2)+2;return Grad;}
if(l2==3){Grad(2,3)=0;return Grad;}
}
if(l1==3)
{
if(l2==1){Grad(3,1)=0;return Grad;}
if(l2==2){Grad(3,2)=0;return Grad;}
if(l2==3){Grad(3,3)=2*x(3)+2;return Grad;}
}
}
A test main program may now be written as:
INT main()
{
int Num,i,j,order,precision,Stop;
// accuracy of the solution either on the function or on the variable
double Accuracy,Accuracy_Variable,Diff_Sol;
INTERVAL_MATRIX SolutionList(200,3);//the list of solutions
INTERVAL_VECTOR TestDomain;//the input intervals for the variable
INTERVAL_VECTOR F(3);
//We set the value of the variable intervals
SetTestDomain (TestDomain);
cerr << "Accuracy on Function = "; cin >> Accuracy;
cerr << "Accuracy on Variable = "; cin >> Accuracy_Variable;
cerr << "Order (0,1)"; cin >>order;
cerr << "Stop at first solutions (0,1,2):";cin>>Stop_First_Sol;
cerr << "Separation between distincts solutions:";cin>> Diff_Sol;
//let's solve....
Num=Solve_General_Gradient_Interval(3,3,IntervalTestFunction,
IntervalGradient,TestDomain,order,10000,Stop,
Accuracy_Variable,Accuracy,Diff_Sol,SolutionList,1);
//too much intervals have been created, this is a failure
if(Num== -1)cout<<"Procedure has failed (too many iterations)"<<endl;
//otherwise print the solution intervals
for(i=1;i<=Num;i++)
{
cout << "solution " << i <<endl;
cout << "x(1)=" << SolutionList(i,1) << endl;
cout << "x(2)=" << SolutionList(i,2) << endl;
cout << "x(3)=" << SolutionList(i,3) << endl;
cout << "Function value at this point" <<endl;
for(j=1;j<=3;j++)F(j)=SolutionList(i,j);
cout << Compute_Interval_Function_Gradient(Dimension,Dimension_Eq,
IntervalTestFunction,
IntervalGradient,
F,1) << endl;
}
return 0;
}
A property of this problem is that the Jacobian of the system is
singular at the solution. Hence the unicity test cannot be verified as
it needs to evaluate the inverse of the jacobian matrix (as will fail
the classical Newton scheme, see section 2.9, that needs also
the inverse Jacobian). But even with
epsilon=epsilonf=1e-6 the algorithm is able to find an
approximation of the solution with 16 boxes only. Interestingly this
is a case where the 3B method is not efficient at all: with the 3B
method the number of boxes increases to over 100 000. This is quite
normal: as the 3B method is used before the interval Newton method it
reduces the range for the unknowns toward a region where the interval
Newton method will fail as the Jacobian is close to a singularity. We
therefore end up with a solving that is only based on the bisection
process and we have seen that this process behaves poorly for this
system. But if we mix the 3B method and the 2B filtering of
section 2.17 then the solving needs only 1 box.
Example 2
The problem we want to solve has been presented in section 2.3.5.2,15.1.1.
The IntervalGradient procedure is:
INTERVAL_MATRIX IntervalGradient (int l1,int l2,INTERVAL_VECTOR & in)
{
INTERVAL_MATRIX Grad(3,3);
INTERVAL x,y,teta;
x=in(1);y=in(2);teta=in(3);
if(l1==1)
{
if(l2==1){Grad(1,1)=2*x;return Grad;}
if(l2==2){Grad(1,2)=2*y;return Grad;}
if(l2==3){Grad(1,3)=0;return Grad;}
}
if(l1==2)
{
if(l2==1){Grad(2,1)=2.0*x-20.0+8.0*Cos(teta);return Grad;}
if(l2==2){Grad(2,2)=2.0*y+8.0*Sin(teta);return Grad;}
if(l2==3){Grad(2,3)=-8.0*x*Sin(teta)+80.0*Sin(teta)+8.0*y*Cos(teta);
return Grad;}
}
if(l1==3)
{
if(l2==1){Grad(3,1)=2.0*x-6.0+4.0*Cos(teta)-4.0*Sin(teta);
return Grad;}
if(l2==2){Grad(3,2)=2.0*y-20.0+4.0*Sin(teta)+4.0*Cos(teta);return Grad;}
if(l2==3){
Grad(3,3)=52.0*Sin(teta)-28.0*Cos(teta)+(4.0*Cos(teta)-
4.0*Sin(teta))*y+(-4.0*Sin(teta)-4.0*Cos(teta))*x;
return Grad;
}
}
}
We may use the same main program as in the previous example
(the name of this program is
Test_Solve_General1_Gradient).
Let's assume that we set epsilonf to 0 and epsilon to 0.01 while looking at all the solutions (Stop=0), using the maximum equation ordering and setting Dist to 0.1. The algorithm provide the following solutions after using 55 boxes:
![\begin{eqnarray*}
&&x=[3.36607,3.37306] y=[6.21468,6.21856] \theta
=[-0.808...
...99845,5.00165] y=[4.99845,5.00146] \theta =[-0.000536641,0]
\end{eqnarray*}](img262.png)
We notice that all of the roots are contained in the solution intervals.
If we use the maximum middle-point equation ordering the algorithm provide the same solution intervals.
With epsilonf=0.001, epsilon=0
the algorithm still find exactly the root
with 55 boxes and a computation time of
7010ms. Here Moore test may have failed as the
solution in ![]() is 0, which correspond exactly to split point in
the bisection process: it may be useful to break the symmetry
in the test domain.
is 0, which correspond exactly to split point in
the bisection process: it may be useful to break the symmetry
in the test domain.
Using the single bisection mode and setting the flag Single_Bisection to 2 enable to reduce the number of boxes to 33 and the computation time to 3580ms for epsilonf=0.00001.
Note that we may improve the efficiency of the procedure by using
simplification procedures such as the 2B (section 2.17)
and the 3B method. In that case for
epsilonf=1e-6, epsilon=1e-6 the number of boxes will have been
reduced to 7. Note that the solution [5,5,0] is still not guaranteed.
But using a search space of ![]() for
for ![]() allow the
Moore test to guarantee both solutions.
allow the
Moore test to guarantee both solutions.
Example 3
This example is derived from example 2. We notice that in the three
equations of example 2 the second degree terms of
INTERVAL_MATRIX IntervalGradient (int l1,int l2,INTERVAL_VECTOR & in)
{
INTERVAL_MATRIX Grad(1,1);
Grad(1,1)=-3788.0+(2692.0+(7576.0-4800.0*Cos(in(1)))*Cos(in(1)))*Cos(in(1))+(
25912.0+(-39320.0+14520.0*Cos(in(1)))*Cos(in(1)))*Sin(in(1));
return Grad;
}
epsilonf=0 and epsilon=0.001
we get the solution by using 8 boxes:
for whatever order. The solution intervals contain the roots of the equation. If we use epsilon=0 and epsilonf=0.1 we get by using 8 boxes:
Here we get a unique solution and a range solution. But we notice that the solution 0 is exactly the middle point of the test domain: Moore test will fail as 0 will always be an end-point of the range. If we break the symmetry of the test domain we will get exactly both solutions.
Example 4
In this example (see section 15.1.3) we deal with a complex problem
of three equations in three unknowns
The system has a solution which is approximatively:
This problem is extremely ill conditioned as for the TestDomain
the functions intervals are:
The name of the test program is Test_Solve_General_Gradient. With espsilonf=0 and epsilon=0.001 and if we stop at the first solution we find with the maximum equation ordering:
with 73 boxes using the direct storage mode (with the reverse storage mode only 37 boxes are needed). With the maximum middle-point equation ordering we find the same intervals with 67 boxes in the direct storage mode (41 for the reverse storage mode).
The importance of normalizing the functions has been mentioned in
section 2.3.5.4. But in this example the use of the Jacobian matrix
enable to drastically reduce the computation time.
If we use epsilonf=0.1 and epsilon=0 and if we stop at the first solution we
find an exact solution using 73 boxes:
in a time which is about 1/100 of the time necessary when we don't use the Jacobian.
In the single bisection smear mode (i.e. only one variable is bisected in the process) the same root is obtained in 21080ms (about 50% less time than when using the full bisection mode) with only 40 boxes in the direct storage mode.
Note that for epsilonf=0.1 and epsilon=0 we find the only root with 73 boxes in 39760ms (41 boxes and 24650ms in the single bisection smear mode).
Note that we may improve the efficiency of the procedure by using simplification procedures such as the 2B (section 2.17) and the 3B method. An interesting point in this example is that the bisection mode 1 (bisecting along the variable whose interval has the largest diameter) is more effective than using the bisection mode 2 (using the smear function) with 53 boxes against 108 for the mode 2 for epsilonf=1e-6 and epsilon=1e-6. This can easily been explained by the complexity of the Jacobian matrix elements that leads to a large overestimation of their values when using interval: in that case the smear function is not very efficient to determine which variable has the most influence on the equations.
General comments
According to the system this procedure may not be especially faster than the general purpose algorithm but the number of necessary boxes is in general drastically reduced. Furthermore the use of Moore test and interval Newton method enable in many cases to determine exactly the solutions.
General purpose solving algorithm with Jacobian and Hessian
Mathematical background
In this new algorithm we will try to improve the evaluation of the function intervals by using the Hessian of the functions. This improvement is based on a sharper analysis of the monotonicity of the functions which in turn is based on a sharper evaluation of the Jacobian matrix of the system. The elementNow consider the corresponding line of the Hessian matrix which is:
The elements of this line indicate the monotonic behavior of the elements of the Jacobian matrix. If some elements in this line have a constant sign, then the elements of the Jacobian are monotonic with respect to some of the unknowns and using this monotonicity we may improve the evaluation of the element of the Jacobian matrix. This improvement has to be applied recursively: indeed as we will evaluate the Jacobian elements for boxes in which some components have now a fixed value the evaluation of the Hessian matrix for these boxes may lead to a larger number of the component of the Hessian which have a constant sign. The recursion will stop if all the component of the Hessian line have a constant sign or if the number of component with a constant sign does not increase.
Note also that not all the function must be differentiable to use this procedure: only one of them is sufficient. In that case you will have however to set special values in the gradient and hessian function (see 2.4.2.2).
We will also use the Hessian in order to try to sharpen the evaluation
of ![]() . Let the box intervals be
. Let the box intervals be
![]() .
Let
.
Let ![]() be the middle point of
be the middle point of
![]() and
and
![]() be the box. Then:
be the box. Then:
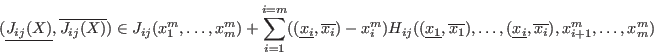 |
(2.5) |
The improvement of the evaluation of the function intervals is due to the fact that a sharper evaluation of the Jacobian matrix may lead to a larger number of Jacobian elements with constant sign than with the direct evaluation of the Jacobian matrix. To speed up the algorithm we store the Jacobian matrix of each box: this enable to avoid the evaluation of the components of the Jacobian matrix which have a constant sign when bisecting the box
Another interest of the Hessian is that it enable to use Kantorovitch theorem. This theorem (see section 3.1.2) can be applied if the number of unknowns is equal to the number of equations and enable to determine boxes in which there is an unique solution, solution which can be found using Newton method (see section 2.9) with as estimate of the solution any point within the boxes.
We will use this theorem at three possible levels:
- level 0: we want solution intervals for which the maximal width is equal or lower than a given threshold. In that case imagine that two solution intervals have been found at some point of the algorithm, this two solutions being close. We will apply Kantorovitch theorem for the center of the two solution intervals. In the most favorable case one of them will contain an unique solution while the boxes given by Kantorovitch theorem will cover the other one: consequently this input intervals will be eliminated of the solution intervals. Therefore Kantorovitch theorem will eliminate spurious solution intervals and we don't need to indicate a minimal distance between the solution intervals.
- level 1: we look for solution intervals whose width has no importance as soon as we are sure that they contain one unique solution which can be found using Newton method with as estimate of the solution any point within the solution intervals. In that case we will apply Kantorovitch theorem for each boxes which appear during the algorithm. If the theorem give a solution intervals we will store it in the solution list and update the remaining boxes of the list so that none of them contain the solution intervals. A consequence is that the width of the solution intervals cannot be determined beforehand while each solution intervals that have been determined using this method contain one unique solution which can be determined using Newton method.
- level 2: we apply Newton method for each box and if Newton converge toward a solution within the current box we store the box as solution interval. The boxes in the list are then filtered so that none of them contains the solution interval.
As for the method using only the gradient we use the Hansen-Sengupta version of the interval Newton method to improve the boxes (see [21]).
Single bisection mode
Instead of bisecting all the variables we may bisect only one of the
variable. The criteria for determining which of the variable will be
bisected is identical to the one presented in section 2.4.1.3
for the mode up to 5. The mode 6 is different: basically we will
bisect the variable having the largest diameter except that it is
supposed that
a weight is assigned to each variable and the diameter used by the
bisection process is the diameter of the range for the variable
multiplied by the weight of the variable. The weight must be indicated
in the vector ALIAS_Bisection_Weight.
Implementation
The generic implementation of this solving procedure is:
int Solve_General_JH_Interval(int Dimension_Var,int Dimension_Eq,
INTEGER_VECTOR &Type_Eq,
INTERVAL_VECTOR (* TheIntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Gradient)(int, int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Hessian)(int, int, INTERVAL_VECTOR &),
INTERVAL_VECTOR & TheDomain,
int Order,
int Iteration,
int Stop_First_Sol,
double Accuracy_Variable,
double Accuracy,
INTERVAL_MATRIX & Solution,
INTEGER_VECTOR & Is_Kanto,
int Apply_Kanto,
int Nb_Max_Solution,INTERVAL_MATRIX &Grad_Init,
int (* Simp_Proc)(INTERVAL_VECTOR &),
int (* Local_Newton)(int Dimension,int Dimension_Eq,
INTERVAL_VECTOR (* TheIntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Gradient)(int, int, INTERVAL_VECTOR &),
VECTOR &Input,double Accuracy,int Max_Iter, VECTOR &Residu,INTERVAL_VECTOR &In))
the arguments being:
- m: number of unknowns
- n: number of functions, see the note 2.3.4.1
- Type_Eq: type of the functions, see the note 2.3.4.2
- IntervalFunction: a function which return the interval vector evaluation of the functions, see the note 2.3.4.3. Remember that if you have equations and inequalities in the system you must first define the equations and then the inequalities.
- IntervalGradient: a function which return the interval matrix of the jacobian of the functions, see the note 2.4.2.2
- IntervalHessian: a function which return the interval matrix of the Hessian of the functions, see the note 2.5.2.1
- TheDomain: box in which we are looking for solution of the system. A copy of the search domain is available in the global variable ALIAS_Init_Domain
- Order: the type of order which is used to store the intervals created during the bisection process. This order may be either MAX_FUNCTION_ORDER or MAX_MIDDLE_FUNCTION_ORDER. See the note on the order 2.3.4.4.
- M: the maximum number of boxes which may be stored. See the note 2.5.2.2
- Stop: the possible values are 0,1,2
- 0: the algorithm will look for every solution in TheDomain
- 1: the algorithm will stop as soon as 1 solution has been found
- 2: the algorithm will stop as soon as Nb solutions have been found
- epsilon: the maximal width of the box, see the note 2.3.4.6
- epsilonf: the maximal width of the function intervals, see the note 2.3.4.6
- Solution: an interval matrix of size (Nb,m)
which will contained the solution intervals. Each solution may be:
- a set of intervals with the associated flag IsKanto to 0:
- a set of intervals with the associated flag IsKanto to 1: there is an unique solution in the set and Newton method will converge toward this solution
- a set of intervals reduced to a point with the associated flag IsKanto to 0: this point is a solution which has been obtained with Krawczyk method (see 2.10). The accuracy of this solution may be improved by using the point as starting point for Krawczyk method and decreasing the accuracy epsilonf
- IsKanto: an integer vector of dimension Nb. A value of 1 for IsKanto(i) indicate that applying Newton method (see section 2.9) with as estimate the center of the solution intervals Solution(i) will converge toward the unique solution which lie within the solution intervals Solution(i)
- ApplyKanto: an integer which indicate at which level we use Kantorovitch theorem. If 1 we use Kantorovitch theorem (see section 3.1.2 and the mathematical background) to determine the solution. A consequence is that the solution interval may have a width larger than epsilon. If 0 we use Kantorovitch theorem just to separate the solutions: the solution interval will have a width epsilon. If 2 we will apply Newton method for every box which has not been eliminated during the bisection process but we will consider the result a solution only if it lie within the box. The maximal number of iteration is determined by the global variable Max_Iter_Newton_JH_Interval (by default 100). In that case we may miss solutions if they are lying inside the same box.
- Nb: the maximal number of solution which will be returned by the algorithm
- GM: an interval matrix which give a-priori information on the values of the derivatives of the function. GM(i,j) is the interval value of the derivative of function i with respect to variable j
- Simp_Proc: a user-supplied procedure that take as input the current box and proceed to some further reduction of the width of the box or even determine that there is no solution for this box, in which case it should return -1 (see note 2.3.3). Remember that you may use the 3B method to improve the efficiency of this algorithm (see section 2.3.2).
- Local_Newton: a Newton scheme that is used when Apply_Kanto is set to 2. When omitted the algorithm will use the ALIAS Newton procedure (see section 2.9).
Note that the following arguments may be omitted:
- Type_Eq: in that case all the functions will supposed to be equations.
- GM: in that case all the derivatives will supposed to be unknown
- Simp_Proc: no simplification procedure is provided by the user
- Local_Newton
The following variables play also a role in the computation:
- ALIAS_Store_Gradient: if not 0 the gradient matrix of each box will be stored together with the boxes. Must be set to 0 for large problem (default value: 1)
- ALIAS_Diam_Max_Gradient: if the maximal width of the ranges in a box is lower than this value, then the gradient will be used to perform the interval evaluation of the functions (default value: 1.e10)
- ALIAS_Diam_Max_Kraw: if the maximal width of the ranges in a box is lower than this value, then the Krawczyk operator will be used to determine if there is a unique solution in the box (default value: 1.e10)
- ALIAS_Diam_Max_Newton: if the maximal width of the ranges in a box is lower than this value, then the interval Newton method will be used either to try to reduce the width of the box or to to ensure that there is no solution of the system in the box (default value: 1.e10)
- ALIAS_Always_Use_Inflation: if ApplyKanto is set
to 1 we get for each solution a box
 which contains only one
solution. If this flag is set to 1 we compute the solution using
Newton and then we use an inflation procedure that try to determine a
box
which contains only one
solution. If this flag is set to 1 we compute the solution using
Newton and then we use an inflation procedure that try to determine a
box 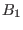 which is larger than
which is larger than 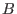 and contains also only one solution
and contains also only one solution
- ALIAS_Eps_Inflation: the inflation algorithm will try to
increase the width of the box
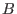 by at least this value
by at least this value
- ALIAS_Sing_Determinant: if the determinant of the jacobian matrix of the system is lower than this value, then the system is supposed to be singular
- ALIAS_Diam_Sing: for a value
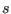 of this
parameter if there is singular solution in the
system, then the algorithm will not look for solution of the system in
a box of width 2
of this
parameter if there is singular solution in the
system, then the algorithm will not look for solution of the system in
a box of width 2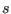 around the singular solution (default value: 0)
around the singular solution (default value: 0)
- ALIAS_Use_Grad_Equation: if this integer array has a
size of n the derivatives of equation
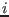 will be used to
evaluate the i-th equation only if ALIAS_Use_Grad_Equation[i]
is not 0
will be used to
evaluate the i-th equation only if ALIAS_Use_Grad_Equation[i]
is not 0
- ALIAS_No_Hessian_Evaluation: if set to 0 we will not use the Hessian to sharpen the interval evaluation of the Gradient when performing the interval evaluation of the equations. This may be useful if its known that the interval evaluation of the elements of the hessian will have always a constant sign
Hessian procedure
The syntax of this function is:
Hess=INTERVAL_MATRIX IntervalHessian (int l1,int l2,INTERVAL_VECTOR & in)This procedure should return an interval matrix of size m
Storage
The boxes generated by the bisection process are stored in
an interval matrix:
Box_Solve_General_Interval(M,m)while the corresponding Jacobian matrix is stored in the interval matrix of size (M, m
Gradient_Solve_JH_IntervalThe purpose of storing the gradient for each box is to avoid to re-compute a gradient as soon as it has been determined that a father of the box has already a gradient with a constant sign. This has the drawback that for large problems this storage will be also large: hence it is possible to avoid this storage by setting the variable ALIAS_Store_Gradient to 0 (its default value is 1). Note that here we store the interval gradient matrix and not the simplified gradient matrix as in the solving procedure involving only the Jacobian.
The algorithm try to manage the storage in order to solve the problem with the given number M (see section 2.3.1.2). As seen in section 2.3.1.2 two storage modes are available, the Direct Storage and the Reverse Storage modes, which are obtained by setting the global variable Reverse_Storage to 0 (the default value) or to the number of unknowns+1.
For both modes the algorithm will first run until the bisection of the current box leads to a total number of boxes which exceed the allowed total number. It will then delete the boxes in the list which have been already bisected, thereby freeing some storage space (usually larger for the reverse mode than for the direct mode) and will start again.
If the procedure has to be used more than once it is possible to speed up the computation by allocating the storage space before calling the procedure. Then you may indicate that the storage space has been allocated beforehand by indicating a negative value for M, the number of boxes being given by the absolute value of M.
Improvement of the function evaluation and of the Jacobian
An improved value of the Jacobian is obtained by taking account its derivative in the procedure:
INTERVAL_MATRIX Compute_Best_Gradient_Interval(int Dimension,
int Dimension_Eq,
INTERVAL_MATRIX (* Gradient)(int, int, INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Hessian)(int, int, INTERVAL_VECTOR &),
INTERVAL_VECTOR &Input,
int Exact,INTERVAL_MATRIX &InGrad)
where
- Exact: if 1 the calculation for one element of the Jacobian will stop as soon as the method has found that the interval evaluation of the element will not have a constant sign. If 0 the best interval evaluation will be computed
- InGrad: if this matrix is not the zero matrix we will assume that the non zero elements of this matrix are the interval evaluation of the Jacobian
To compute only the best value of the jacobian element at l-th row nad j-th column you may use:
INTERVAL Compute_Best_Gradient_Interval_line(int l,int j,int Dim,
int Dimension_Eq,
INTERVAL_MATRIX (* Gradient)(int, int, INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Hessian)(int, int, INTERVAL_VECTOR &),
INTERVAL_VECTOR &Input,int Exact)
We may also obtain the best interval evaluation of the equations through the procedure
INTERVAL_VECTOR Compute_Interval_Function_Gradient(int Dimension,
int Dimension_Eq,
INTERVAL_VECTOR (* TheIntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Gradient)(int, int, INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Hessian)(int, int, INTERVAL_VECTOR &),
INTERVAL_VECTOR &Input, int Exact)
Return code and debug
The procedure will return an integer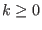 : number of solutions
: number of solutions
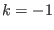 : the size of the storage is too low (
possible solutions: increase M,
or use the 3B method, or use the reverse storage mode or the single
bisection mode)
: the size of the storage is too low (
possible solutions: increase M,
or use the 3B method, or use the reverse storage mode or the single
bisection mode)
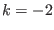 : m or n is not strictly positive
: m or n is not strictly positive
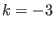 : Order is not 0 or 1
: Order is not 0 or 1
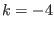 : one of the function in the system has not a type 0, -1
or 1 (i.e. it's not an equation, neither inequality
: one of the function in the system has not a type 0, -1
or 1 (i.e. it's not an equation, neither inequality 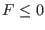 or an
inequality
or an
inequality 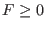 )
)
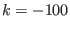 : in the mixed bisection mode the number of variables
that will be bisected is larger than the number of unknowns
: in the mixed bisection mode the number of variables
that will be bisected is larger than the number of unknowns
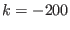 : one of the value of ALIAS_Delta3B or
ALIAS_Max3B is negative or 0
: one of the value of ALIAS_Delta3B or
ALIAS_Max3B is negative or 0
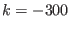 : one of the value of ALIAS_SubEq3B is not 0 or 1
: one of the value of ALIAS_SubEq3B is not 0 or 1
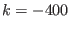 : although ALIAS_SubEq3B has as size the number of
equations none of its components is 1
: although ALIAS_SubEq3B has as size the number of
equations none of its components is 1
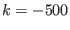 : ALIAS_ND is different from 0 (i.e. we are
dealing with a non-0 dimensional problem, see the corresponding
chapter) and the name of the result file has not been specified
: ALIAS_ND is different from 0 (i.e. we are
dealing with a non-0 dimensional problem, see the corresponding
chapter) and the name of the result file has not been specified
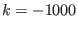 : the value of the flag Single_Bisection is not
correct
: the value of the flag Single_Bisection is not
correct
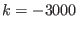 : we use the full bissection mode and the problem has
more than 10 unknowns
: we use the full bissection mode and the problem has
more than 10 unknowns
Examples
Example 2
The problem we want to solve has been presented in
section 2.3.5.2 and section 15.1.1.
The name of the test program is Test_Solve_JH_General1.
If epsilonf=0.01 the program using the maximum equation ordering find the two solutions using 50 boxes.
If we use the single bisection smear mode the program using the maximum equation ordering find the two solutions in 4260ms using 32 boxes.
Note that we may improve the efficiency of the procedure by using
simplification procedures such as the 2B (section 2.17)
and the 3B method. In that case for
epsilonf=1e-6, epsilon=1e-6 the number of boxes will have been
reduced to 2 and both solutions will be guaranteed.
even with a search space of ![]() for
for ![]() .
.
Example 3
This example is derived from example 2 and has been presented in section 2.3.5.3. The test program is Test_Solve_JH_General2. The IntervalFunction and IntervalGradient have been presented before. The IntervalHessian is:
INTERVAL_MATRIX IntervalHessian (int l1,int l2,INTERVAL_VECTOR & in)
{
INTERVAL_MATRIX Hess(1,1);
Hess(1,1)=39320.0+(-3128.0+(-78640.0+43560.0*Cos(in(1)))*
Cos(in(1)))*Cos(in(1))+(-2692.0+(-15152.0+14400.0*Cos(in(1)))*
Cos(in(1)))*Sin(in(1));
return Hess;
}
A test main program may be written as:
INT main()
{
int Iterations,Dimension,Dimension_Eq,Apply_Kanto;
int Num,i,j,order,Stop_First_Sol,precision,niter,nn;
double Accuracy,Accuracy_Variable,eps;
INTERVAL_MATRIX SolutionList(200,3);
INTERVAL_VECTOR TestDomain,F(1),P(1),H(3);
VECTOR TR(1),Residu(1);
INTEGER_VECTOR Is_Kanto(6);
Dimension_Eq=Dimension=1;SetTestDomain (TestDomain);
cerr << "Number of iteration = "; cin >> Iterations;
cerr << "Accuracy on Function = "; cin >> Accuracy;
cerr << "Accuracy on Variable = "; cin >> Accuracy_Variable;
cerr << "Debug Level (0,1,2)="; cin >> Debug_Level_Solve_General_Interval;
cerr << "Order (0,1)="; cin >>order;
cerr << "Stop at first solutions (0,1,2)=";cin>>Stop_First_Sol;
cerr << "Apply Kanto (0,1)=";cin>>Apply_Kanto;
Num=Solve_General_JH_Interval(Dimension,Dimension_Eq,
IntervalTestFunction,IntervalGradient,IntervalHessian,
TestDomain,order,Iterations,Stop_First_Sol,Accuracy_Variable,
Accuracy,SolutionList,Is_Kanto,Apply_Kanto,6);
if(Num== -1){cout << "The procedure has failed (too many iterations)"<<endl;return 0;}
cout << Num << " solution(s)" << endl;
for(i=1;i<=Num;i++)
{
cout<<"solution "<<i<<endl;cout<<"teta="<<SolutionList(i,1)<<endl;
cout << "Function value at this point" <<endl;F(1)=SolutionList(i,1);
cout << Compute_Interval_Function_Gradient(Dimension,Dimension_Eq,
IntervalTestFunction,IntervalGradient,
IntervalHessian,F,1) << endl;
cout << "Function value at middle interval" <<endl;
P(1)=Mid(SolutionList(i,1)); F=IntervalTestFunction(1,Dimension_Eq,P);
cout << Sup(F(1)) << endl; TR(1)=Mid(SolutionList(i,1));
if(Is_Kanto(i)==1)cout << "This solution is Kanto" <<endl;
else cout << "This solution is not Kanto" << endl;
if(Kantorovitch(Dimension,IntervalTestFunction,IntervalGradient,
IntervalHessian,TR,&eps)==1)
{
P(1)=INTERVAL(TR(1)-eps,TR(1)+eps);
cout << "Unique solution in: " <<P << endl;
}
if(Is_Kanto(i)==1)
{
nn=Newton(Dimension,IntervalTestFunction,IntervalGradient,TR,Accuracy,1000,Residu);
if(nn>0)
{
cout << "Newton iteration converge toward: " << endl;
cout << TR << "with residu= " << Residu<< endl;
}
else
{
if(nn==0)cout << "Newton does not converge" << endl;
if(nn== -1)cout<<"Newton has encountered a singular matrix"<<endl;
}
}
}
return 0;
}
With epsilonf=0.0001 and epsilon=0.001 , using Kantorovitch at
level 1,
we get the solution
intervals, using 4 boxes:
Newton method initialized with the center of these boxes converge toward 4.08282e-15 and -0.8067834.
Example 4
In this example (see section 15.1.3) we deal with a complex problem
of three equations in three unknowns
![]() .
We are looking for a solution in the domain:
.
We are looking for a solution in the domain:
The system has a solution which is approximatively:
This problem is extremely ill conditioned as for the TestDomain the equations intervals are:
The name of the test program is Test_Solve_JH_General.
If we use epsilonf=0.1 and epsilon=0, we get the first solution with the following number of boxes and computation time:
| full bisection | smear bisection | |
| direct storage | 71, 31200ms | 38, 20220ms |
| reverse storage | 35, 14710ms | 38, 20280ms |
Note that we may improve the efficiency of the procedure by using simplification procedures such as the 2B (section 2.17) and the 3B method. An interesting point in this example is that the bisection mode 1 (bisecting along the variable whose interval has the largest diameter) is more effective than using the bisection mode 2 (using the smear function) with 33 boxes against 38 for the mode 2 for epsilonf=1e-6 and epsilon=1e-6. This can easily been explained by the complexity of the Jacobian matrix elements that leads to a large overestimation of their values when using interval: in that case the smear function is not very efficient to determine which variable has the most influence on the equations. But it must be noted that the use of the Hessian allows to reduce this overestimation and consequently the differences in term of used boxes between the two bisection mode is slightly reduced compared to the one we have observed when using only the Jacobian (see section 2.4.3.4).
Stopping the general solving procedures
It may be interesting to stop the solving procedures although the algorithm has not been completed. We have already seen that a possible mean to do that was to specify a number of roots in such way that the procedure will exit as soon it has found this number of roots.
Another possible way to stop the calculation is to use a time-out mechanism. For that purpose you may define in the double ALIAS_TimeOut the maximum number of minutes allowed for the calculation. If this number is reached (approximatively) the procedure will exit and will set the flag ALIAS_TimeOut_Activated to 1.
The solution that have been found by the algorithms are stored in the interval matrix ALIAS_Solution and their number is ALIAS_Nb_Solution. Note that for the procedures involving the Jacobian this matrix will usually describes the boxes that include a unique solution.
Ridder method for solving one equation
Mathematical background
Ridder method is an iterative scheme used to obtain one root of the equationunder the assumption
Implementation
Ridder's method enable to find a root of an equation
int Ridder(REAL (* TheFunction)(REAL),INTERVAL &Input,
double AccuracyV,double Accuracy,int Max_Iter,double *Sol, double *Residu)
with:
- TheFunction: a procedure which enable to compute the value of the equation at a given point
- Input: the interval
![$[x_1,x_2]$](img280.png) in which we are looking
for a root
in which we are looking
for a root
- AccuracyF: a threshold on the minimal value of the width of the
interval
![$[x_k, x_{k+1}]$](img289.png) with
with
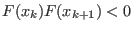 considered during the procedure
considered during the procedure
- Accuracy: a threshold on the value of
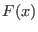 which
determine a root of the equation
which
determine a root of the equation
- MaxIter: maximal number of iteration
- Sol: on success the value of the root
- Residu: the value of the equation at Sol
- 1: a solution has been found as F(Sol)
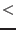 Accuracy
Accuracy
- 2: a solution has been found as
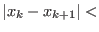 AccuracyV
AccuracyV
- -1:
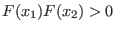
- -2: a numerical error was encountered during the computation
- -3: the maximal number of iteration has been reached without finding a solution
Brent method for solving one equation
Mathematical background
Brent method is an iterative scheme used to obtain one root of the equationwith:
![\begin{eqnarray*}
R&=&
\frac{F(x_3)}{F(x_2)} S=\frac{F(X_3)}{F(x_1)} T=\f...
...\\
P&=&S[T(R-T)(x_2-x_3)-(1-R)(x_3-x_1)]\\
Q&=&(T-1)(R-1)(S-1)
\end{eqnarray*}](img296.png)
In this method
Implementation
Brent's method enable to find a root of an equation
int Brent(REAL (* TheFunction)(REAL),INTERVAL &Input,
double AccuracyV,double Accuracy,int Max_Iter,double *Sol, double *Residu)
with:
- TheFunction: a procedure which enable to compute the value of the equation at a given point
- Input: the interval
![$[x_1,x_2]$](img280.png) in which we are looking
for a root
in which we are looking
for a root
- AccuracyF: a threshold on the minimal value of the width of the
interval
![$[x_k, x_{k+1}]$](img289.png) with
with
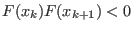 considered during the procedure
considered during the procedure
- Accuracy: a threshold on the value of
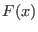 which
determine a root of the equation
which
determine a root of the equation
- MaxIter: maximal number of iteration
- Sol: on success the value of the root
- Residu: the value of the equation at Sol
- 1: a solution has been found as F(Sol)
 Accuracy
Accuracy
- 2: a solution has been found as
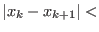 AccuracyV
AccuracyV
- -1:
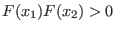
- -3: the maximal number of iteration has been reached without finding a solution
Newton method for solving systems of equations
Mathematical background
Let ![]() be a system of
be a system of ![]() equations in the
equations in the ![]() unknowns
unknowns ![]() and
and ![]() be an estimate of the solution of the system.
Let
be an estimate of the solution of the system.
Let ![]() be the Jacobian matrix of the system of equation. Then
the iterative scheme defined by:
be the Jacobian matrix of the system of equation. Then
the iterative scheme defined by:
| (2.6) |
A simplified Newton method consist in using a constant matrix in
the classical Newton method, for example the inverse Jacobian matrix
at some point like ![]() . The iterative scheme become:
. The iterative scheme become:
| (2.7) |
Newton method has advantages and drawbacks that need to be known in order to use it in the best way:
- it may really be fast: this may be important, for example in real-time control
- it is very simple to use
- but it does not necessarily converge toward the solution "closest" to the estimate (see the example in section 15.1.2)
- but it may not converge. Kantorovitch theorem (see section 3.1.2) enable to determine the size of the convergence ball but this size is usually small (but quite often in practice the size is greater than the size given by the theorem which however is exact in some cases)
- but a numerical implementation of Newton may overflow
Implementation
The procedure for using Newton method is:
int Newton(int n,VECTOR (* TheFunction)(VECTOR &),
MATRIX (* Gradient)(VECTOR &),
VECTOR &Input,double Accuracy,int MaxIter,VECTOR &Residu)
with
- n: number of equations
- TheFunction: a procedure which return the value of the equation for given values of the unknowns (see note 2.3.4.3)
- Gradient: a procedure which return the Jacobian matrix of the system for given values of the unknowns (see note 2.4.2.2)
- Input: at the start of the procedure the estimate of the solution, at the end of the procedure the solution
- Accuracy: the procedure return a solution if there is an
Input such that
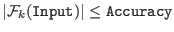 for all
for all  in [1,
in [1,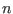 ].
].
- MaxIter: the procedure will return a failure code if a solution is not found after MaxIter iteration
- Residu: the value of the equations for the solution
Note that it also possible to use in the Newton method the interval evaluation of the equation and of the Jacobian matrix which are necessary for the general purpose solving algorithm with Jacobian (see section 2.4). The syntax of this implementation is:
int Newton(int Dimension,
INTERVAL_VECTOR (* IntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* IntervalGradient)(int, int, INTERVAL_VECTOR &),
VECTOR &Input,double Accuracy,int MaxIter,VECTOR &Residu)
- IntervalFunction: a function which return the interval vector evaluation of the equations, see the note 2.3.4.3
- IntervalGradient: a function which the interval matrix of the jacobian of the equations, see the note 2.4.2.2
To avoid overflow problem it is possible to use the vectors ALIAS_Newton_Max_Dim, (ALIAS_Newton_Min_Dim) that must be resized to the number of unknowns and in which will be indicated the maximal (minimal) possible value of each variable after each Newton operation. If one of these values is exceeded Newton will return 0.
The version of Newton method with constant ![]() matrix is
implemented as:
matrix is
implemented as:
int Newton(int n,VECTOR (* TheFunction)(VECTOR &),
MATRIX &InvGrad,VECTOR &Input,double Accuracy,int MaxIter,VECTOR &Residu)
There is a special implementation of Newton method for univariate
polynomial int Newton(int Degree,REAL *Input,VECTOR &Coeff,double Accuracy,int Max_Iter,REAL *Residu)with:
- Degree: degree of the polynomial
- Input: on entry an estimate of the solution and on exit the solution
- Coeff: coefficient of the polynomial ordered in increasing degree
- Accuracy: Input is a solution if |
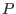 (Input|
(Input|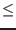 Accuracy
Accuracy
- MaxIter: the procedure will return a failure code if a solution is not found after MaxIter iteration
- Residu: the value of the polynomial for the solution
An example of use of the Newton method is presented in section 15.1.1, where it is compared to alternative methods.
Return value
- -1: A singular matrix has been found during the scheme (not
applicable if we use Newton with a constant
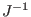 )
)
- 0: Newton has not converged after MaxIter iteration
- 1: Newton has converged toward solution Input
- 2: only valid for the implementation in which the function evaluation return an interval vector. It has not been possible to find a solution such that all the mid point of the interval evaluation of the function was at a distance less than Accuracy from 0. However the procedure will return as solution the point obtained during Newton iteration for which the interval evaluation of all the function include 0 and has the minimal average value for the width of the interval evaluation of the functions.
Functions
The procedures TheFunction and IntervalFunction should be
user written. They return the value
of the equations (either as a vector of REAL
or as a vector of INTERVAL, see 2.3.4.3) for given values
or intervals
for the unknowns.
They take one argument which is the vector of REAL which
describe the unknowns.
In the same way the procedures Gradient and IntervalGradient should be user written. They return the Jacobian matrix of the system of equations of the equations (either as a matrix of REAL or as a matrix of INTERVAL) for given values of the unknowns. The Gradient procedure take one argument which is the vector of REAL which describe the unknowns. The IntervalGradient procedure has three arguments and is described in section 2.4.2.2.
Systematic use of Newton
It may be interesting to systematically use the Newton scheme in a solving procedure in order to quickly determine the solutions of a system of equations.
For that purpose we may use the TryNewton procedure whose purpose is to run a few iterations of the Newton scheme for a given box. The syntax of this procedure is:
int TryNewton(int DimensionEq,int DimVar,
INTERVAL_VECTOR (* TheIntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Gradient)(int, int, INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Hessian)(int, int, INTERVAL_VECTOR &),
double Accuracy,
int MaxIter,
INTERVAL_VECTOR &Input,
INTERVAL_VECTOR &Domain,
INTERVAL_VECTOR &UnicityBox)
where
- DimensionEq: number of equations
- DimVar: number of variables
- TheIntervalFunction: a procedure in MakeF format for computing an interval evaluation of the equations
- Gradient: a procedure that compute the jacobian in MakeJ format
- Hessian: a procedure in MakeH format that computes the Hessian of the system
- Domain: the domain in which we are looking for solutions of the system
- Input: a sub-box of Domain
If the Newton scheme converges, the presence of a single solution in the neighborhood of the approximated solution is checked by using the Kantorovitch theorem (see section 3.1.2). If this check is positive, then a ball that includes this single solution is determined and returned in UnicityBox. If the flag ALIAS_Epsilon_Inflation is set to 1, then the inflation scheme is used to try to enlarge this unicity box.
This procedure returns 11 if an unicity box has been determined, 0 otherwise. Note that this procedure is already embedded in HessianSolve.
Krawczyk method for solving systems of equations
Mathematical background
Let ![]() be a system of
be a system of ![]() equations in the
equations in the ![]() unknowns
unknowns ![]() . Let
. Let ![]() be a range vector for
be a range vector for ![]() and
and
![]() . Let
. Let ![]() be the norm of the matrix
be the norm of the matrix
![]() . Let
the following iterative scheme for
. Let
the following iterative scheme for ![]() :
:
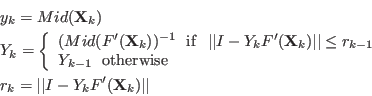
Let define
If
then the previous iterative scheme will converge to the unique solution of
Implementation
The procedure is implemented as:
int Krawczyk_Solver(int m,int n,
INTERVAL_VECTOR (* IntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* IntervalGradient)(int, int, INTERVAL_VECTOR &),
INTERVAL_VECTOR &Input,double Acc , VECTOR &Result)
with
- m: the number of unknown
- n: the number of equations
- IntervalFunction: a function which return the interval vector evaluation of the equations, see the note 2.3.4.3
- IntervalGradient: a function which the interval matrix of the jacobian of the equations, see the note 2.4.2.2
- Input: the ranges for the variables
- Acc: the algorithm will return the result if
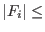 Acc
Acc
- Result: the solution of the system
Solving univariate polynomial with interval analysis
Mathematical background
Clearly interval analysis may be used for solving univariate polynomial, especially if we are looking for some roots within a specific interval (note that for generic polynomial we may always obtain intervals in which lie the positive and negative roots using the algorithm described in section 5.2).
Implementation
The algorithm we have implemented is a direct derivation of the general purpose solving algorithm with Jacobian and Hessian in which these values are automatically derived. To isolate the roots we use the Kantorovitch theorem (which may also optionally be used during the resolution, see section 3.1.2). To eliminate boxes during the bisection process we use the safe Budan-Fourier method (see section 5.5.2).
int Solve_UP_JH_Interval(int Degree,VECTOR Coeff,
INTERVAL & TheDomain,
int Order,int M,int Stop,
double epsilon,double epsilonf,
INTERVAL_VECTOR & Solution,
INTEGER_VECTOR & IsKanto,int NbSolution);
with:
- Degree: degree of the polynomial
- Coeff: the Degree+1 coefficients of the polynomial in increasing degree
- TheDomain: the interval in which we are looking for roots
- Order: the type of order which is used to store the intervals created during the bisection process. This order may be either MAX_FUNCTION_ORDER or MAX_MIDDLE_FUNCTION_ORDER. See the note on the order 2.3.4.4.
- M: the maximum number of boxes which may be stored. See the note 2.5.2.2
- Stop: the possible values are 0,1,2
- 0: the algorithm will look for every solution in TheDomain
- 1: the algorithm will stop as soon as 1 solution has been found
- 2: the algorithm will stop as soon as Nb solutions have been found
- epsilon: the maximal width of the box, see the note 2.3.4.6
- epsilonf: the maximal width of the equation intervals, see the note 2.3.4.6
- Solution: an interval matrix of size (Nb,m) which will contained the solution intervals.
- IsKanto: an integer vector of dimension Nb. A value of 1 for IsKanto(i) indicate that Newton method (see section 2.9) with as estimate the center of some solution interval Solution(i) has been used and has converged toward the unique solution Solution(i) which lie within this solution intervals. Note that the interval which contain the solution may be retrieved in the interval vector Interval_Solution_UP.
- NbSolution: the maximum number of solution we are looking for.
int Solve_UP_JH_Interval(int Degree,VECTOR Coeff,
int Order,int M,int Stop,
double epsilon,double epsilonf,
INTERVAL_VECTOR & Solution,
INTEGER_VECTOR & Is_Kanto,int NbSolution);
There are two alternate forms of this procedure in the case where we are
looking for the positive or negative roots of the polynomial.
int Solve_UP_JH_Positive_Interval int Solve_UP_JH_Negative_IntervalIn the three previous procedures there is no TestDomain as it is automatically determined by the procedure. If there was a failure in the determination of the domain (for the reasons explained in section 5.2) the procedures will return -1.
The previous procedures are numerically safe in the sense that we take into account rounding errors in the evaluation of the polynomial and its gradient. For well conditioned polynomials you may use faster procedures whose name has the prefix Fast. For example Fast_Solve_UP_JH_Interval is the general procedure for finding the roots of a polynomial.
Clearly this procedure is not intended to be used as substitute to more classical algorithms.
It makes use of a specific Krawczyk procedure for polynomials:
int Krawczyk_UP(int Degree,INTERVAL_VECTOR &Coeff,
INTERVAL_VECTOR &CoeffG,INTERVAL &Input)
Example
The program Test_Solve_UP is a general test program which
enable to solve univariate polynomial whose coefficients are given in
a file by increasing power of the unknown.
We use as example the Wilkinson polynomial of degree ![]() where
where ![]() :
:

It is well known that this polynomial is extremely ill-conditioned. For
For ![]() and if we are looking for the roots in the interval
[0,2] the computation time is 90ms, for
and if we are looking for the roots in the interval
[0,2] the computation time is 90ms, for ![]() 190ms and 330ms for
190ms and 330ms for ![]() .
For the fast algorithm these times are: 10ms, 20ms, 30 ms
Note that the best classical solving algorithm start to give
inaccurate results for
.
For the fast algorithm these times are: 10ms, 20ms, 30 ms
Note that the best classical solving algorithm start to give
inaccurate results for ![]() (between 12.5 and 18.5 the interval
analysis algorithm finds the roots
13.424830, 13.538691, 15.477653, 15.498664, 17.554518, 17.553513)
and give imaginary roots for
(between 12.5 and 18.5 the interval
analysis algorithm finds the roots
13.424830, 13.538691, 15.477653, 15.498664, 17.554518, 17.553513)
and give imaginary roots for ![]() .
.
Solving univariate polynomial numerically
As an alternative to interval solving ALIAS proposes a numerical algorithm
ALIAS_Solve_Poly((double *C, int *Degree,double *Sol),The arguments are the coefficients C of the polynomial, a pointer to the integer Degree that is initially the degree of the polynomial and Sol which will be used to store the real roots. This procedure returns the number of real roots or -1 if the computation has failed. The procedure ALIAS_Solve_Poly_PR takes the same arguments but returns the real part of the roots.
There is also a version of the Newton scheme for univariate polynomial:
int Fast_Newton(int Degree,REAL *Input,VECTOR &Coeff,VECTOR &CoeffG,
double Accuracy,int Max_Iter,REAL *Residu)
where
- Degree is the degree of the polynomial
- Input: an approximation of the solution
- Coeff: the polynomial is written as Coeff[1]+Coeff[2]x+.....Coeff[Degree+1]pow(x,Degree)
- CoeffG: the coefficients of the derivative of the polynomial
- Accuracy: the algorithm will stop if the absolute value of the evaluation of the polynomial at the current point is lower than this number
- Max_Iter: maximum number of iteration
- Residu: the value of the polynomial at the solution
Solving trigonometric equation
Mathematical background
The purpose of this section is to present an algorithm which enable to determine the roots of an equation| (2.8) |
Then we have:
Note that the change of variable is not valid if
Using the above relation any trigonometric equation can be transformed into a polynomial equation which is solved using the tools of section 2.11.
It remains to define an interval for angles that we will denote
an angle interval.
The element of an angle interval is usually defined between 0 and
![]() (although in most of the following procedures any value can be
used when not specified: internally the element of the angle
interval are converted into value within this range). A difference
between numbers interval (INTERVAL) and angle interval is that
the lower bound of an angle interval may be larger than the upper bound.
Indeed the order in an angle interval is
important: for example the angle intervals [0,
(although in most of the following procedures any value can be
used when not specified: internally the element of the angle
interval are converted into value within this range). A difference
between numbers interval (INTERVAL) and angle interval is that
the lower bound of an angle interval may be larger than the upper bound.
Indeed the order in an angle interval is
important: for example the angle intervals [0,![]() ] and [
] and [![]() ,0]
are not the same.
,0]
are not the same.
Implementation
The purpose of this procedure is to determine the roots of a trigonometric equation within a given angle interval.
int Solve_Trigo_Interval(int n,VECTOR &A,INTEGER_VECTOR &SSin,
INTEGER_VECTOR &CCos,double epsilon,double epsilonf,
int M,int Stop,INTERVAL_VECTOR &Solution,int Nb,REAL Inf,REAL Sup);
with:
- M: the maximum number of boxes which may be stored. See the note 2.3.4.5
- Stop: the possible values are 0,1,2
- 0: the algorithm will look for every solution in the angle interval
- 1: the algorithm will stop as soon as 1 solution has been found
- 2: the algorithm will stop as soon as Nb solutions have been found
- epsilon: the maximal width of the box, see the note 2.3.4.6
- epsilonf: the maximal width of the equation intervals, see the note 2.3.4.6
- Solution: an interval vector of size at least Nb which will contained the solution intervals.
- Nb: the maximal number of solution which will be returned by the algorithm
- Inf, Sup: the bound of the angle interval in which we are looking for solutions.
 0: the number of roots
0: the number of roots
- -1: the bound Inf or Sup is incorrect (positive or negative infinity)
int Solve_Trigo_Interval(int n,VECTOR &A,INTEGER_VECTOR &SSin,
INTEGER_VECTOR &CCos,double epsilon,double epsilonf,
int M,int Stop,INTERVAL_VECTOR &Solution,int Nb);
This procedure first analyze the trigonometric equation to find bounds
on the roots using the algorithm described in
section 4.3, then use the previous procedure to
determine the roots within the bound. In some case this procedure may
be faster than the general purpose algorithm.
Examples
The test program Test_Solve_Trigo enable to determine the roots of any trigonometric equation which is described in a file. In this you indicate first the coefficient of the term, its sine power and then its cosine power, this for each term of the equation.
We consider the trigonometric equation derived in section 15.1.2:
which has 0,5.47640186917958647 as roots. The general procedure find the roots 1.743205553711625e-11, 5.476401869153828 while the procedure using the determination of the bounds (which are [0,1.570796326794896], [5.235987755982987,6.283185307179586]) find the roots 5.974250609803587e-12, 5.476401869153828.
Solving systems with linear and non-linear terms: the simplex
method
Mathematical background
Consider a system ofHence the system is now a linear system with the additional constraint that
In our case we may use only phase I or phase I and II
by considering the ![]() optimum problems which are to
determine the minimum and maximum of the
optimum problems which are to
determine the minimum and maximum of the ![]() unknowns under the
unknowns under the
![]() constraints
constraints
![]() and update the interval for an
unknown if the simplex applied to minimize or maximize enable to
improve the range. It may be seen that this is a
recursive procedure: an improvement on one variable change the
constraint equations and may thus change the result of the simplex
method applied for determining the extremum of a variable which has
already been considered.
and update the interval for an
unknown if the simplex applied to minimize or maximize enable to
improve the range. It may be seen that this is a
recursive procedure: an improvement on one variable change the
constraint equations and may thus change the result of the simplex
method applied for determining the extremum of a variable which has
already been considered.
This procedure, proposed in [25], enable to correct one of the drawback of the general solving procedures: each equation is considered independently and for given intervals for the unknowns two equations may have an interval evaluation that contain 0 although these equations cannot be canceled at the same time. The previous method enable to take into account at least partly the dependence of the equations. Clearly it will more efficient if the functions has a large number of linear terms and a "small" non-linear part.
In all of the following procedures the various storage mode and bisection mode of the general solving procedures may be used and inequalities are handled.
Implementation without gradient
The procedure is implemented as:
int Solve_Simplex(int m,int n,int NbNl,
INTEGER_VECTOR TypeEq,
INTERVAL_VECTOR (* IntervalFunction)(int,int,INTERVAL_VECTOR &),
void (* NonLinear)(INTERVAL_VECTOR &x,INTERVAL_VECTOR &X),
void (* CoeffLinear)(MATRIX &U),
double MaxDiam,
int FullSimplex,
INTERVAL_VECTOR & TheDomain,
int Order,int Iteration,int Stop,
double epsilon,double epsilonf,double Dist,
INTERVAL_MATRIX & Solution,int Nb,
int (* Simp_Proc)(INTERVAL_VECTOR &))
the arguments being:
- m: number of unknowns
- n: number of equations, see the note 2.3.4.1
- NbNl: number of equations that have no linear term at all or are inequalities. If you omit this parameter its value will be assumed to be 0 and you have to omit the TypeEq parameter.
- TypeEq: an array of integers that indicate the type for
the equations. TypeEq(i) is -1,0,1 if equation i is an
inequality
 , an equation or an inequality
, an equation or an inequality 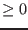 .
.
- IntervalFunction: a function which return the interval vector evaluation of the equations, see the note 2.3.4.3 on how to write this procedure. The equations must be ordered: first the equations with linear terms then the equations without any linear terms and finally the inequalities
- NonLinear: a procedure to compute the non linear part of the equations, see note 2.14.2.1
- CoeffLinear: a procedure that return a matrix which contain the constant coefficients of the linear term in the equation, see note 2.14.2.2
- MaxDiam: the simplex method will not be used on boxes whose maximal width is lower than this value. Should be set to 0 or a small value
- FullSimplex: this flag is used to indicate how much we
will
use the simplex method (which may be costly). If set to -1 only the
phase I of the simplex will be used. If set to
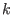 with
with 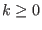 , then
the full simplex method will be used recursively on the
, then
the full simplex method will be used recursively on the 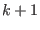 variables having the largest interval width.
variables having the largest interval width.
- TheDomain: box in which we are looking for solution of the equations
- Order: the type of order which is used to store the intervals created during the bisection process. This order may be either MAX_FUNCTION_ORDER or MAX_MIDDLE_FUNCTION_ORDER. See the note on the order 2.3.4.4.
- M: the maximum number of boxes which may be stored. See the note 2.3.4.5
- Stop: the possible values are 0,1,2
- 0: the algorithm will look for every solution in TheDomain
- 1: the algorithm will stop as soon as 1 solution has been found
- 2: the algorithm will stop as soon as Nb solutions have been found
- epsilon: the maximal width of the solution intervals, see the note 2.3.4.6
- epsilonf: the maximal width of the equation intervals for a solution, see the note 2.3.4.6
- Dist: minimal distance between the middle point of two interval solutions, see the note 2.3.4.7
- Solution: an interval matrix of size (Nb,m) which will contained the solution intervals. This list is sorted using the order specified by Order
- Nb: the maximal number of solution which will be returned by the algorithm
- Simp_Proc: a user-supplied procedure that take as input the current box and proceed to some further reduction of the width of the box or even determine that there is no solution for this box, in which case it should return -1 (see note 2.3.3). Remember that you may use the 3B method to improve the efficiency of this algorithm (see section 2.3.2).
Note that the Simp_Proc argument may be omitted.
The NonLinear procedure
The purpose of the procedure is to compute an interval evaluation of
the non linear term of the equations (the 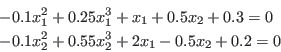
The non-linear terms of these equations are
void NonLinear(INTERVAL_VECTOR &x,INTERVAL_VECTOR &X)
{
X(1) = (-0.1+0.25*x(1))*Sqr(x(1));
X(2) = (-0.1+0.55*x(2))*Sqr(x(2));
}
The CoeffLinear procedure
This procedure returns a matrix
void CoeffLinear(MATRIX &U)
{
U(1,1)=1; U(1,2)=0.5; U(1,3)=0.3;
U(2,1)=2; U(1,2)=-0.5; U(1,3)=0.2;
}
Using an expansion
In some case it may be interesting to consider an expansion of the function around a given point. For example consider the termYou may also prohibit the use of the simplex method in the procedure (for example to use it only in your own simplification procedure) by setting the flag ALIAS_DONT_USE_SIMPLEX to 1.
Example
The main program for the previous system of 2 equations (omitting the procedure F that computes the interval evaluation of the equations) will be written as
int main()
{
int num,i;
INTERVAL_MATRIX Solution(100,2);
INTERVAL_VECTOR x(2);
INTEGER_VECTOR Type(2);
Clear(Type);
for(i=1;i<=2;i++)x(i)=INTERVAL(-10,10);
Single_Bisection=1;
num=Solve_Simplex(2,2,0,Type,F,NonLinear,CoeffLinear,0.001,0,x,
0,40000,0,0.,0.0001,0.0001,Solution,100);
for(i=1;i<=num;i++)
{
x(1)=Solution(i,1);x(2)=Solution(i,2);
cout<<"Solution "<<i<<":"<<x<<endl;
}
}
Implementation with gradient
This procedure may be used if the gradient of the equations are available. A full version is implemented as:
int Solve_Simplex_Gradient(int m,int n,int NbNl,
INTEGER_VECTOR TypeEq,
INTERVAL_VECTOR (* IntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Gradient)(int, int,INTERVAL_VECTOR &),
void (* NonLinear)(INTERVAL_VECTOR &x,INTERVAL_VECTOR &X),
void (* GradientNonLinear)(INTERVAL_VECTOR &x,INTERVAL_MATRIX &X),
void (* CoeffLinear)(MATRIX &U),
double MaxDiam,
int FullSimplex,
INTERVAL_VECTOR & TheDomain,
int Order,int Iteration,int Stop,
double epsilon,double epsilonf,double Dist,
INTERVAL_MATRIX & Solution,
int Nb,int UseGradNL,
INTEGER_MATRIX &GI,
int (* Simp_Proc)(INTERVAL_VECTOR &))
the arguments being:
- m: number of unknowns
- n: number of equations, see the note 2.3.4.1
- NbNl: number of equations that have no linear term at all or are inequalities.
- TypeEq: an array of integers that indicate the type for
the equations. TypeEq(i) is -1,0,1 if equation i is an
inequality
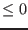 , an equation or an inequality
, an equation or an inequality 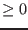 .
.
- IntervalFunction: a function which return the interval vector evaluation of the equations, see the note 2.3.4.3 on how to write this procedure. The equations must be ordered: first the equations with linear terms then the equations without any linear terms and finally the inequalities
- Gradient: a procedure which return the Jacobian matrix of the system for given values of the unknowns (see note 2.4.2.2)
- NonLinear: a procedure to compute the non linear part of the equations, see note 2.14.2.1
- GradientNonLinear: a procedure that returns the gradient of the non linear part of the equations, see note 2.14.3.1
- CoeffLinear: a procedure that return a matrix which contain the constant coefficients of the linear term in the equation, see note 2.14.2.2
- MaxDiam: the simplex method will not be used on boxes whose maximal width is lower than this value. Should be set to 0 or a small value
- FullSimplex: this flag is used to indicate how much we
will
use the simplex method (which may be costly). If set to -1 only the
phase I of the simplex will be used. If set to
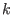 with
with 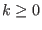 , then
the full simplex method will be used recursively on the
, then
the full simplex method will be used recursively on the 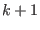 variables having the largest interval width.
variables having the largest interval width.
- TheDomain: box in which we are looking for solution of the equations
- Order: the type of order which is used to store the intervals created during the bisection process. This order may be either MAX_FUNCTION_ORDER or MAX_MIDDLE_FUNCTION_ORDER. See the note on the order 2.3.4.4.
- M: the maximum number of boxes which may be stored. See the note 2.3.4.5
- Stop: the possible values are 0,1,2
- 0: the algorithm will look for every solution in TheDomain
- 1: the algorithm will stop as soon as 1 solution has been found
- 2: the algorithm will stop as soon as Nb solutions have been found
- epsilon: the maximal width of the solution intervals, see the note 2.3.4.6
- epsilonf: the maximal width of the equation intervals for a solution, see the note 2.3.4.6
- Dist: minimal distance between the middle point of two interval solutions, see the note 2.3.4.7
- Solution: an interval matrix of size (Nb,m) which will contained the solution intervals. This list is sorted using the order specified by Order
- Nb: the maximal number of solution which will be returned by the algorithm
- UseGradNL: if set to 1 the algorithm will use the gradient of the non linear part of the equations to improve their interval evaluation. Otherwise must be set to 0.
- GI: an integer matrix which give a-priori information on
the sign of the derivative of the function. GI(i,j) indicates
the sign of the derivative of function i with respect to
variable j using the following code:
- -1: the derivative is always negative
- 0: the function is not dependent of variable j
- 1: the derivative is always positive
- 2: the sign of the derivative is not known
- Simp_Proc: a user-supplied procedure that take as input the current box and proceed to some further reduction of the width of the box or even determine that there is no solution for this box, in which case it should return -1 (see note 2.3.3). Remember that you may use the 3B method to improve the efficiency of this algorithm (see section 2.3.2).
- ALIAS_Store_Gradient: if not 0 the gradient matrix of each box will be stored together with the boxes. Must be set to 0 for large problem (default value: 1)
- ALIAS_Diam_Max_Gradient: if the maximal width of the ranges in a box is lower than this value, then the gradient will be used to perform the interval evaluation of the functions (default value: 1.e10)
- ALIAS_Diam_Max_Kraw: if the maximal width of the ranges in a box is lower than this value, then the Krawczyk operator will be used to determine if there is a unique solution in the box (default value: 1.e10)
- ALIAS_Diam_Max_Newton: if the maximal width of the ranges in a box is lower than this value, then the interval Newton method will be used either to try to reduce the width of the box or to to ensure that there is no solution of the system in the box (default value: 1.e10)
- Min_Diam_Simplex: if the maximal width of the input box is lower than this value, then the simplex method will be used
- Max_Diam_Simplex: if the maximal width of the input box is lower than this value, then the simplex method will not be used
- Min_Improve_Simplex: when applying the simplex method if the change on one variable is larger than this value, then the simplex method will be repeated
- ALIAS_Simplex_Expanded: if set to 1 the expression has been expanded with respect to the lower bound of each variable
There are several versions of this procedure in which several arguments of the general procedure may be omitted. The following table indicates which arguments may be omitted and the corresponding assumptions (EO=equations only).
| omitted | ||||||
| NbNl | 0 | 0 | 0 | |||
| TypeEq | EO | EO | EO | EO | EO | EO |
| GradientNonLinear | not known | not known | ||||
| UseGradNL | 0 | 0 | 0 | 0 |
The GradientNonLinear procedure
The purpose of this procedure is to compute the jacobian of the non
linear part of the equations in order to improve their interval
evaluation. The syntax of this procedure is:
void GradientNonLinear(INTERVAL_VECTOR &x,INTERVAL_MATRIX &J)where x is an interval vector which contains the range for the unknowns and J is the corresponding jacobian interval matrix.
Solving systems with determinants
In some cases systems may involve determinants: for example in
algebraic geometry the resultant of two algebraic equations is defined
as the determinant of the Sylvester matrix. To get an analytical form
of the equations it is therefore necessary to compute the
determinant: but in some cases this may be quite difficult as the
expression may be quite large, even for sparse matrix. A mechanism in
ALIAS enable to get the interval evaluation of an equation
which include determinant without having to provide the analytical
form of the determinant but only the interval evaluation of the
components of the matrix. This mechanism is based on procedures that
compute the interval evaluation of the determinant of an
interval-valued matrix (see section 7.1).
Using these procedures it is possible to design the equation
evaluation procedure that are used in the general solving procedure of
ALIAS as described in 2.3.4.3. Assume for example that
you have to evaluate the
expression
where A, B are two matrices of dimension 6. Assume that V is an interval vector which contain the interval values for
INTERVAL_MATRIX A(6,6),B(6,6); A=Compute_A(V) //compute A for the interval value of x,y B=Compute_B(V) //compute B for the interval value of x,y W(1)=(V(1)+Medium_Determinant(A))*V(2)+2*(V(2)+Medium_Determinant(B));You must be however careful when using this procedure in a denominator as the presence of 0 in the interval evaluation of the determinant is not checked, which will lead to an error when computing the interval evaluation of an equation (see section 2.1.1.3).
Note that the MakeF procedure of the ALIAS-Maple package is able to produce efficient code for an equation file even if unexpanded determinants are present in the equation.
There are also procedures to compute the derivatives of a determinant Note that the MakeJ procedure of the ALIAS-Maple package is able to produce a procedure compatible with the requirements of the gradient procedure required by the library (see section 2.4.2.2) even if determinants are present in the equation.
There are also procedures to compute the second order derivatives of a determinant Note that the MakeH procedure of the ALIAS-Maple package is able to produce a procedure compatible with the requirements of the hessian procedure required by the library (see section 2.5.2.1) even if determinants are present in the equation.
Solving systems of distance equations
Principle
We consider here a special occurrence of quadratic equations that describe distances between points in an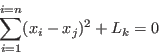
where
Equations involving
virtual points may be written as:
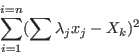
where the
The method proposed in ALIAS to solve this type of systems is based on the general procedure using the gradient and hessian. A first difference is that it is not necessary to provide the gradient and hessian function as they are easily derived from the system of equations. Note also that due to the particular structure of the distance equations the interval evaluation leads to exact bounds. Furthermore the algorithm we propose uses a special version of Kantorovitch theorem (i.e. a version that produces a larger ball with a unique solution in it compared to the general version of the theorem), an interval Newton method, a specific version of the simplex method described in section 2.14 and a specific version of the inflation method described in section 3.1.6 (i.e. a method that allows to compute directly the radius of a ball around a solution that will contain only this solution). In addition two simplification rules are used:
- as each function is a sum of square term each of them involving different unknowns we verify if the interval evaluation of the term has a positive part (in the opposite case the current box is discarded) and we may update the unknowns so that the negative part of the term is reduced (this is basically an application of the concept of 2B-consistency). Hence the procedures described in section 2.17 should not be used for distance equations.
- based on the triangle equation: each subset of equations describing the distances between a set of 3 points is detected and the algorithm verify if the triangle equation is satisfied and, in some cases may update the boxes.
Implementation
A system ofwhere the maximal number of square term is
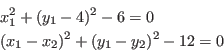
In that case APOW, ACONS, LI will be:
The two first elements of the first row of APOW (1, 0) describes the first square term of the first equation and state that it is
Consider now function involving virtual points. Each square term may
thus be written as:
where
the third row of APOW will be (-1 0 -2 0), the third row of ACONS will be (0 3 0 1) and the third row of LI will be -10. AVARV will have 2 row and 4 columns and is given as:
Among the
int Solve_Distance(int DimVar,int DimEq,
INTEGER_VECTOR &Type_Eq,
INTEGER_MATRIX &APOW,MATRIX &ACONS,VECTOR &LI,
int p,int k,MATRIX &AVARV,
INTERVAL_VECTOR & TheDomain,
int M,
double epsilonf,
int Stop,
INTERVAL_MATRIX & Solution,int Nb,
int (* Simp_Proc)(INTERVAL_VECTOR &))
The arguments are:
- DimVar: number of unknowns
- DimEq: number of equations and inequalities in the system
- Type_Eq: an integer array of dimension DimEq where
the j-th element indicates if the j-th function is an equation (value
=0), an inequality
 (value = -1) or an inequality
(value = -1) or an inequality  (value = 1)
(value = 1)
- p: number of functions involving virtual points
- k: number of virtual points
- TheDomain: box in which we are looking for solution of the system
- M: the maximum number of boxes which may be stored. In the algorithm we use the reverse storage mode except if the global integer ALIAS_Parallel_Slave is set to 1 (its default value is 0)
- epsilonf: either the maximal width of the function intervals for a solution if it is not determined by using Newton scheme or the accuracy used in the Newton scheme
- Stop: the possible values are 0,1,2
- 0: the algorithm will look for every solution in TheDomain
- 1: the algorithm will stop as soon as 1 solution has been found
- 2: the algorithm will stop as soon as Nb solutions have been found
- Solution: an interval matrix of size (Nb,m) which will contained the solution intervals. This list is sorted using the order specified by Order
- Nb: the maximal number of solution which will be returned by the algorithm
- Simp_Proc: a user-supplied procedure that take as input the current box and proceed to some further reduction of the width of the box or even determine that there is no solution for this box, in which case it should return -1 (see note 2.3.3). Remember also that you may use the 3B method to improve the efficiency of this algorithm (see section 2.3.2).
The following variables play also a role in the computation:
- ALIAS_Diam_Max_Kraw: if the maximal width of the ranges in a box is lower than this value, then the Krawczyk operator will be used to determine if there is a unique solution in the box (default value: 1.e10)
- ALIAS_Diam_Max_Newton: if the maximal width of the ranges in a box is lower than this value, then the interval Newton method will be used either to try to reduce the width of the box or to to ensure that there is no solution of the system in the box (default value: 1.e10)
- ALIAS_Permute_List: if the value of this flag is
 the
algorithm will permute the current list with the largest box in the
list of boxes to process (as the algorithm uses systematically the
Newton scheme with as initial guess the center of the current box
permutation may allow to find quickly new solutions)
the
algorithm will permute the current list with the largest box in the
list of boxes to process (as the algorithm uses systematically the
Newton scheme with as initial guess the center of the current box
permutation may allow to find quickly new solutions)
Return code
This procedure will return: : number of solutions
: number of solutions
- -1: storage space exceeded
- -2: DimVar or DimVar is a negative number
- -4: an element in Type_Eq is not 0, -1 or 1
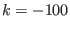 : in the mixed bisection mode the number of variables
that will be bisected is larger than the number of unknowns
: in the mixed bisection mode the number of variables
that will be bisected is larger than the number of unknowns
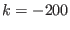 : one of the value of ALIAS_Delta3B or
ALIAS_Max3B is negative or 0
: one of the value of ALIAS_Delta3B or
ALIAS_Max3B is negative or 0
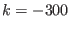 : one of the value of ALIAS_SubEq3B is not 0 or 1
: one of the value of ALIAS_SubEq3B is not 0 or 1
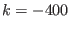 : although ALIAS_SubEq3B has as size the number of
equations none of its components is 1
: although ALIAS_SubEq3B has as size the number of
equations none of its components is 1
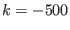 : ALIAS_ND is different from 0 (i.e. we are
dealing with a non-0 dimensional problem, see the corresponding
chapter) and the name of the result file has not been specified
: ALIAS_ND is different from 0 (i.e. we are
dealing with a non-0 dimensional problem, see the corresponding
chapter) and the name of the result file has not been specified
Inflation and Newton scheme
For the distance equations we use a specific procedure for the inflation method (see section 3.1.6). Indeed in that case it is possible to calculate directly the diameter of the largest ball centered at an approximation of a solution that contains one and only one solution. The procedure is:
int ALIAS_Epsilon_Inflation(int Dimension,int Dimension_Eq,
INTEGER_MATRIX &APOW,MATRIX &ACONS,
VECTOR &LI,
int NB_EQV,int NB_VARV,MATRIX &AVARV,
VECTOR &Amid,
INTERVAL_VECTOR &P,
INTERVAL_VECTOR &PP1,
int type,double epsilon,
int (* Simp_Proc)(INTERVAL_VECTOR &))
We have also a specific implementation of the Newton scheme:
int Newton_Fast(int Dimension,int Dimension_Eq,
INTEGER_MATRIX &APOW,MATRIX &ACONS,VECTOR &LI,
int NB_EQV,int NB_VARV,MATRIX &AVARV,
VECTOR &Input,double Accuracy,int Max_Iter,VECTOR &Residu)
Choosing the right set of equations and variables
For the best efficiency the unknowns has to be well chosen, especially so that the jacobian of the system has full rank at a solution. The use of virtual point should be systematic to avoid having a system that is singular at a solution.
Initial domain and simplification procedures
A specific procedure Bound_Distance
for
finding an initial estimate of the search
domain has been implemented in the ALIAS-Maple
package (
see the ALIAS-Maple manual): this procedure may provide an initial guess
for the solution ranges or improve a given guess.
Note also that the choice of the right coordinate system (for example its origin) and which points should be defined as virtual points may have a large influence on the computation time (see an example in [10]).
Filtering a system of equation
As mentioned previously the 2B heuristic to improve the solving is to rewrite each equation as the equality of two different terms, to determine if the interval evaluation of both terms are consistent and if not to adjust the interval for one term and by using the inverse function for this term to improve the width for one or more unknowns.
For example imagine that one of the equation is
![]() . The procedure will introduce a new variable
. The procedure will introduce a new variable ![]() such
that
such
that ![]() and compute its interval evaluation. If
and compute its interval evaluation. If ![]() has a
negative upper bound the equation has no solution for the current
range for
has a
negative upper bound the equation has no solution for the current
range for ![]() . If the upper bound
. If the upper bound ![]() of
of ![]() is positive then the inverse function of
is positive then the inverse function of ![]() indicates that
indicates that ![]() should
lie in
should
lie in
![]() : we may then update the interval for
: we may then update the interval for
![]() if this is not
the case. If the lower bound
if this is not
the case. If the lower bound ![]() of
of ![]() is positive then the inverse function of
is positive then the inverse function of ![]() indicates that
indicates that ![]() should
lie outside
should
lie outside
![]() . If the range for
. If the range for ![]() is included
in this interval, then there is no solution to the equation for this
range for
is included
in this interval, then there is no solution to the equation for this
range for ![]() .
.
Note:
- this 2B consistency is implemented in ALIAS-Maple by the procedure HullConsistencyStrong
- the HullConsistency procedure of ALIAS-Maple may seem to
be redundant with HullConsistencyStrong. This is not the case as
HullConsistency implements a simplification of the left hand
term of the equation that is not performed by HullConsistencyStrong. For example for the equation
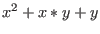 HullConsistencyStrong will rewrite the equation as
HullConsistencyStrong will rewrite the equation as
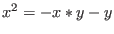 while HullConsistency will use
while HullConsistency will use
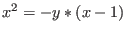 which will lead to a better interval evaluation of
the left hand term
which will lead to a better interval evaluation of
the left hand term