La page de J-P. Merlet

J-P. Merlet home page

La page Présentation de HEPHAISTOS

HEPHAISTOS home page

La page "Présentation" de l'INRIA

INRIA home page

Subsections

• Management of boxes list
  • Adding boxes to a list
  • Freeing boxes in a list
  
  
• Void procedures
• Bisection procedures
• 3B procedures
• Volume of a box
• Filtering
  • Square adjustment
  
  
• Box reduction
• Binomial

Miscellaneous procedures

Management of boxes list

Adding boxes to a list

The procedure ALIAS_Add_Box allows to add boxes to a list:

 
int ALIAS_Add_Box(int DimVar,INTERVAL_MATRIX &Box,int *Current_Box,int *Nb_Box,
         INTERVAL_MATRIX New_Box, int Nb_New_Box,int MaxBox)

where

• DimVar: number of ranges in the box
• Box: the list of box
• Current_Box: the insertion point for the new boxes
• Nb_Box: the current number of boxes in the list. Afterward the new number of boxes in the list
• New_Box: the list of boxes to add
• Nb_New_Box: the number of boxes to add
• MaxBox: the maximal number of boxes in the list

If Reverse_Storage is set to 0 the new boxes will be added at the end of the list. Otherwise all the boxes to add that are smaller (i.e. have a smaller width or if the width are identical a smaller mean diameter) than the box in position Current_Box+1 in the list are added to the list starting at position Current_Box.

There is a similar procedure if the simplified jacobian is also stored:

 
int ALIAS_Add_Box_Gradient(int DimVar,int DimEq,INTERVAL_MATRIX &Box,
             INTEGER_MATRIX &GBox,
             int *Current_Box,int *Nb_Box,
             INTERVAL_MATRIX New_Box, 
             INTEGER_MATRIX GNew_Box,int Nb_New_Box,int MaxBox)

where

• GBox: the list of simplified jacobian
• GNew_Box: the simplified jacobian of the new boxes

If the jacobian is stored instead of the simplified jacobian you may use

 
int ALIAS_Add_Box_Hessian(int DimVar,int DimEq,INTERVAL_MATRIX &Box,
                   INTERVAL_MATRIX &GBox,
                   int *Current_Box,int *Nb_Box,
                   INTERVAL_MATRIX New_Box, 
                   INTERVAL_MATRIX GNew_Box,int Nb_New_Box,int MaxBox)

Freeing boxes in a list

An algorithm is currently processing box Current in the list: hence box from 1 to Current -1 are free. The procedure

 
void ALIAS_Free_Storage(int *Current,int *nb_box,int DimVar,int DimEq,
             INTERVAL_MATRIX &Box,INTERVAL_MATRIX &GBox)

allows to free this unused storage by shifting: the box initially at position Current will become box number 1.

Void procedures

In some cases the routine of ALIAS-C++ have procedure arguments that are useless. ALIAS-C++ proposes void procedures that may be used as such argument and have no effect on the calculation:

• int ALIAS_Simp_Proc_Void: a simplification procedure that always return 0
• INTERVAL_MATRIX ALIAS_Gradient_Void(int l1,int l2,INTERVAL_VECTOR &P): a gradient procedure that returns a not defined interval matrix
• int ALIAS_Matrix_Void(INTERVAL_VECTOR &Box,INTERVAL_MATRIX &P): a procedure that may be used for routine asking for a matrix but the return code is 0, stating that the matrix has not been computed
• INTERVAL_MATRIX Hessian_Void(int i1, int i2, INTERVAL_VECTOR &X): a procedure that returns an empty (1,1) interval matrix
• void Compute_Gradient_Non_Linear_Void(INTERVAL_VECTOR &X,INTERVAL_MATRIX &J): a procedure for the simplex algorithm that is empty
• INTERVAL_VECTOR ALIAS_Void_Update_Range(double z,INTERVAL_VECTOR &Input): a Range procedure for the continuation algorithm that just returns Input

Bisection procedures

We indicate here the program used for the bisection in the general solving procedures with the abbreviation SG Solve_General_Interval, SGG for Solve_General_Gradient_Interval and SJH for Solve_General_JH_Interval. All procedures return the number of the variable that will be bisected (a return code of 0 or lower is an error message). .

SG, mode 1, 3, 4, SGG, SJH, mode 1:

 
int Select_Best_Direction_Interval_Fast(int Dim,INTERVAL_VECTOR &Input)

where Dim is the number of unknowns and Input is the box

SG, mode 2, SGG, mode 6:

 
int Select_Best_Direction_Interval(int Dim,int Dimension_Eq,int Order,
          INTERVAL_VECTOR (*Func)(int,int,INTERVAL_VECTOR &), 
          INTERVAL_VECTOR &Input)

where Dimension_Eq is the number of equations and Order the current ordering mode of the boxes.

SGG, SJH, mode 2:

 
int Select_Best_Direction_Smear(int Dim,int Dimension_Eq,
                INTERVAL_VECTOR (* Func)(int,int,INTERVAL_VECTOR &), 
                INTERVAL_MATRIX (* Gradient)(int, int, INTERVAL_VECTOR &), 
                INTERVAL_VECTOR &Input)

where Func is the name of the procedure that interval evaluates the equations and Gradient the procedure that evaluates the derivative of the equations.

SGG, SJH, mode 3:

 
int Select_Best_Direction_Smear_Bounded(int Dim,int Dimension_Eq,
              double Bound,
              INTERVAL_VECTOR (* Func)(int,int,INTERVAL_VECTOR &), 
              INTERVAL_MATRIX (* Gradient)(int, int, INTERVAL_VECTOR &), 
              INTERVAL_VECTOR &Input)

where Bound represents ALIAS_Bound_Smear.

SGG, SJH, mode 4:

 
int Select_Best_Direction_Gradient_Interval(int Dim,int Dimension_Eq,
                INTERVAL_VECTOR (* Func)(int,int,INTERVAL_VECTOR &), 
                INTERVAL_MATRIX (* Gradient)(int, int, INTERVAL_VECTOR &), 
                INTERVAL_VECTOR &Input, double *SINDEX)

where SINDEX is the criteria value.

SG, SGG, SJH, mode 5:

 
int Select_Best_Direction_Interval_Round_Robin(int Dim,INTERVAL_VECTOR &Input)

SG, mode 6:

 
int Select_Best_Direction_Grad(int Dim,int Dimension_Eq,
                   INTERVAL_VECTOR (* Func)(int,int,INTERVAL_VECTOR &), 
                   INTERVAL_VECTOR &Input)

SJH, mode 6:

 
int Select_Best_Direction_Weight(int DimVar,INTERVAL_VECTOR &Input)

SGG, mode 7:

 
int Select_Best_Direction_Interval_Proc(int Dim,int Dimension_Eq,
                int Nb_Var,int Order,
                INTERVAL_VECTOR (* Func)(int,int,INTERVAL_VECTOR &), 
                INTERVAL_VECTOR &Input,int (* Simp_Proc)(INTERVAL_VECTOR &))

where Nb_Var is set to 1.

We have a specific bisection procedure for the distance equations that corresponds to mode 1 of SG:

 
int Select_Best_Direction_Distance(int Dimension,int Dimension_Eq,
                 INTEGER_MATRIX &APOW,
                 MATRIX &ACONS,VECTOR &LI,
                 int NB_EQV,int NB_VARV,MATRIX &AVARV,
                 INTERVAL_VECTOR &Input,double *SPLIT)

where SPLIT is the bisection point.

A specific version of the smear procedure is used for determining the condition number of a matrix (mode 2):

 
int Select_Best_Direction_Smear_CN(int Dim,int Dimension_Eq,
                 INTERVAL_VECTOR (* Func)(int,int,INTERVAL_VECTOR &), 
                 INTERVAL_MATRIX (* Gradient)(int, int, INTERVAL_VECTOR &), 
                 INTERVAL_VECTOR &Input)

Similarly there is a special mode 2 for the procedures dealing the with the eigenvalues of a matrix:

 
int Select_Best_Direction_Smear_Eigen(int Dim,int Dimension_Eq,
                  INTERVAL_VECTOR (* Func)(int,int,INTERVAL_VECTOR &), 
                  INTERVAL_MATRIX (* Gradient)(int, int, INTERVAL_VECTOR &), 
                  INTERVAL_VECTOR &Input)

You may define your own bisection procedure by setting the variable Single_Bisection to 20 while having defined the procedure:

 
int Select_Best_Direction_Interval_User(int DimVar,int DimEq,
INTERVAL_VECTOR (* TheIntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_VECTOR &Input)

where DimVar is the size of the unknown vector, DimEq the number of equations, TheIntervalFunction the evaluation function of your problem and Input the current box. This procedure shall return the variable number that will be bisected.

If you are not using this possibility you still need to define this procedure as:

 
int Select_Best_Direction_Interval_User(int DimVar,int DimEq,
INTERVAL_VECTOR (* TheIntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_VECTOR &Input)
{
;
}

An example of bissection procedure is given below. The counter randa counts the number of bissection performed by the branch and bound algorithm and we have defined a bissection threshold limranda and if

• rand=limranda we use the smear bissection procedure
• rand=2limranda we bissect the largest interval for the variable 13 to 20
• rand=3limranda we bissect the largest interval for the variable 1 to 12 and reset randa to 0
• otherwise the largest interval of all variables is bissected

 
int randa=0;
int limranda=4;
int Select_Best_Direction_Interval_User(int DimVar,int Nb_Eq,
	INTERVAL_VECTOR (* TheIntervalFunction)(int,int,INTERVAL_VECTOR &),
	INTERVAL_VECTOR &Input)
{
  int i,j,jj,k,randa;
  double amax,amax1;

  amax=Diam(Input(1));
  jj=1;
  for(i=1;i<=36;i++)
    {
      amax1=Diam(Input(i));
      if(amax1>amax)
	{
	  amax=amax1;
	  jj=i;
	}
    }

  randa++;
      if(randa==limranda)
	{
	  k=Select_Best_Direction_Smear(36,36,1,FNEWTON_FK8,JNEWTON_FK8,
					    Input);
	  return k;
	}
      if(randa==2*limranda)
	{
	  amax=Diam(Input(13));
	  k=13;
	  for(i=13;i<=20;i++)
	    {
	      if(Diam(Input(k))>amax){amax=Diam(Input(k));k=i;}
	    }
	  return k;
	}
      if(randa==3*limranda)
	{
	  amax=Diam(Input(1));
	  k=1;
	  for(i=1;i<=12;i++)
	    {
	      if(Diam(Input(k))>amax){amax=Diam(Input(k));k=i;}
	    }
	  randa=0;
	  return k;
	}
      return jj;
}

3B procedures

The 3B procedures are implemented according to the solving algorithms. For Solve_General_Interval:

 
int ALIAS_3B_Normal(int Dimension,int DimEq,
                   INTERVAL_VECTOR (* Func)(int,int,INTERVAL_VECTOR &), 
                   INTERVAL_VECTOR &Input,int (* Simp_Proc)(INTERVAL_VECTOR &))

where

• Dimension: number of unknowns
• DimEq: number of equations
• Func: procedure to evaluate the equations
• Input: the current box
• Simp_Proc: an optional simplification procedure

For Solve_General_Gradient_Interval:

 
int ALIAS_3B_Gradient(int DimVar,int DimEq,
                   INTERVAL_VECTOR (* Func)(int,int,INTERVAL_VECTOR &), 
                   INTERVAL_MATRIX (* Gradient)(int, int, INTERVAL_VECTOR &), 
                   INTERVAL_VECTOR &Input,INTEGER_VECTOR &A1,
                   int (* Simp_Proc)(INTERVAL_VECTOR &))

whereGradient is the name of the procedure that evaluate the derivatives of the equations

For Solve_General_JH_Interval:

 
int ALIAS_3B_Hessian(int DimVar,int DimEq,
                   INTERVAL_VECTOR (* Func)(int,int,INTERVAL_VECTOR &), 
                   INTERVAL_MATRIX (* Gradient)(int, int, INTERVAL_VECTOR &), 
                   INTERVAL_MATRIX (* Hessian)(int, int, INTERVAL_VECTOR &), 
                   INTERVAL_VECTOR &Input,INTERVAL_MATRIX &A1,
                   int (* Simp_Proc)(INTERVAL_VECTOR &))

where Hessian is the procedure that computes the Hessian of the equations.

A specific 3B exists for distance equations:

 
int ALIAS_3B_Distance(int Dim,int Dimension_Eq,
                  INTEGER_VECTOR &VAR_TOUCHED,
                  INTEGER_MATRIX &APOW,MATRIX &ACONS,
                  VECTOR &LI,int NB_EQV,int NB_VARV,MATRIX &AVARV,
                  INTERVAL_VECTOR &Input,int (* Simp_Proc)(INTERVAL_VECTOR &))

For the eigenvalue of matrices we have:

 
int ALIAS_3B_EigenValues(int Dimension,int Dimension_Eq,int Degree,
                    int (* TheMatrix)(INTERVAL_VECTOR &, INTERVAL_MATRIX &), 
                    int Has_Matrix,
                    INTERVAL_VECTOR (* Func)(int,int,INTERVAL_VECTOR &), 
                    int *Has_Gradient,
                    INTERVAL_MATRIX (* Gradient)(int, int,INTERVAL_VECTOR &), 
                    INTERVAL_VECTOR (* TheCoeff)(INTERVAL_VECTOR &), 
                   int Nb_Points,int Use_Solve,
                   double Accuracy,double Accuracy_Var,
                    INTERVAL_VECTOR &Input,
                    int (* Solve_Poly)(double *, int *,double *), 
                    int (* Simp_Proc)(INTERVAL_VECTOR &))

For the geometry of region with given eigenvalue range we have:

 
int ALIAS_3B_Min_Max_EigenValues_Area(int Degree,int Nb_Parameter,
                    INTERVAL_VECTOR (* TheCoeff)(INTERVAL_VECTOR &), 
                    INTERVAL_VECTOR (* TheCoeffCentered)(INTERVAL_VECTOR &,double), 
                    int Nb_Constraints,INTEGER_VECTOR &Type_Eq,
                    int (* TheMatrix)(INTERVAL_VECTOR &, INTERVAL_MATRIX &), 
                    int Has_Matrix,
                    INTERVAL_VECTOR (* Func)(int,int,INTERVAL_VECTOR &), 
                    int *Has_Gradient,
                    INTERVAL_MATRIX (* Gradient)(int, int,INTERVAL_VECTOR &), 
                    double *Seuil_First_Sol1,int RealRoot,
                    int (* Solve_Poly)(double *, int *,double *), 
                    INTERVAL_VECTOR &Input,
                    int (* Simp_Proc)(INTERVAL_VECTOR &))

For the optimum of the condition number of matrices we have:

 
int ALIAS_3B_CN(int Dimension,int Dimension_Eq,int Degree,
                    int (* TheMatrix)(INTERVAL_VECTOR &, INTERVAL_MATRIX &), 
                    int Has_Matrix,
                    INTERVAL_VECTOR (* Func)(int,int,INTERVAL_VECTOR &), 
                    int Has_Gradient,
                    INTERVAL_MATRIX (* Gradient)(int, int,INTERVAL_VECTOR &), 
                    INTERVAL_VECTOR (* TheCoeff)(INTERVAL_VECTOR &), 
                    int Nb_Points,int Absolute,
                    double Accuracy,double Accuracy_Var,
                    INTERVAL_VECTOR &Input,
                    int (* Solve_Poly)(double *, int *,double *), 
                    int (* Simp_Proc)(INTERVAL_VECTOR &))

In the procedure ALIAS_Geometry_Carre we use:

 
int ALIAS_3B_Constraints(int Nb_Parameter,int Dimension_Eq,
                    INTEGER_VECTOR &Type_Eq,INTEGER_VECTOR &Imperatif,
                    int Degree,double Accuracy_Variable,double Accuracy,
                    double Accuracy_Geometry,
                    INTERVAL_VECTOR (* F)(int,int,INTERVAL_VECTOR &), 
                    int *Has_Gradient,
                    INTERVAL_MATRIX (* Gradient)(int, int,INTERVAL_VECTOR &),
                    INTERVAL_VECTOR &Input,
                    int (* Simp_Proc)(INTERVAL_VECTOR &))

Volume of a box

The procedure ALIAS_Volume allows to compute the volume of a box. It has 2 syntax:

 
double ALIAS_Volume(int Dim,INTERVAL_VECTOR &Box)
double ALIAS_Volume(int Dim,int box,INTERVAL_MATRIX &BOX)

The first syntax allows to compute the volume of the interval vector Box of size Dim, while the second syntax allows to compute the volume of the box defined by the box-th row of the interval matrix BOX: the row is supposed to have Dim elements.

Filtering

Square adjustment

Assume that an equation is written as $(x-W)^2=U$ where $U,W$ are intervals and $x$ lie in the interval [LOW, HIGH]. According to the interval values LOW and HIGH may not be compatible with the equation. The procedure ALIAS_Ajuste_Square allows one to obtain new bounds for the range for $x$:

 
int ALIAS_Ajuste_Square(INTERVAL &U,INTERVAL &W,double *LOW,double *HIGH)

This procedure will return:

• -1 if 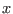$x$ cannot be a solution of the equation
• 1 if new values have been found for LOW and/or HIGH
• 2 if the sum of the absolute value of the change between the initial value of LOW, HIGH and their new value is greater than ALIAS_Seuil_Ajuste or if this sum is larger than the initial diameter of 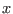$x$ multiplied by ALIAS_Seuil_Ajuste_Percent divided by 100
• 0 otherwise

Box reduction

Let Sol be a solution of a system that has been found in the box B while the algorithm was processing a list of boxes BOX. It is of interest to treat the box and the list of boxes in such way that Sol is no more included in the set of boxes i.e. to have in the list of boxes only the complementary of each box with respect to the box Sol. Note that for a problem with $n$ unknowns this complementary may be described by up to $2n$ boxes.

This may be obtained by using:

int Sol_Reduction(int Dimension,int Dimension_Eq,
                INTERVAL_MATRIX &BOX,
               INTERVAL_VECTOR &B, INTERVAL_VECTOR &Sol,
               int *nb,int type,
               int (* Simp_Proc)(INTERVAL_VECTOR &))

where

• nb: the total number of boxes in the list BOX
• type: allow to create at most type new boxes that will be appended to BOX
• Simp_Proc: a simplification procedure for the system

This algorithm will return -1 if the solution box covers completely the box B. Note that this algorithm may create new boxes but only ALIAS_Allows_N_New_Boxes are allowed to be created (with a default value of 2). A similar procedure exists when gradient boxes have also to be stored:

 
int Sol_Reduction(int Dimension_Var,int Dimension_Eq,
  INTERVAL_MATRIX &BBOX,
  INTERVAL_MATRIX &GBBOX,
  INTERVAL_MATRIX (* Gradient)(int, int,INTERVAL_VECTOR &), 
  INTERVAL_VECTOR &P, INTERVAL_VECTOR &PP1,
  int current_box,int *nb_box,
  int nb_max_box,int type,
  int (* Simp_Proc)(INTERVAL_VECTOR &))

where

• GBBOX: the gradient boxes
• current_box: the number of the current box
• nb_box: the total number of boxes
• nb_max_box: the maximal number of new boxes that can be created
• type: if nb_max_box is lower than 2Dimension_Var then the full complementary boxes cannot be generated. Hence the boxes that will be generated will still have an intersection with PP1. But the set of generated boxes will depend on the order in which the variables are considered when generating the new boxes. type allows one to specify this order. If set to 1 the algorithm will consider the variables according to the width of their range, the largest first. If set to 2 it will consider the variable according to their influence in the sense of the smear function (see section 2.4.1.3. For any other value the variables will be considered in the order of their definition.

Note that in the Solve_General_Gradient_Interval and Solve_General_JH_Interval we use for nb_max_box the value of ALIAS_Allows_N_New_Boxes (with a default value of 2) and for type the value of ALIAS_Type_N_New_Boxes (default value of 0)

Binomial

The calculation of $C_n^m$ may be done with the procedure

 
int Binomial(int n,int m)

J-P. Merlet home page

La page Présentation de HEPHAISTOS

HEPHAISTOS home page

La page "Présentation" de l'INRIA

INRIA home page