Analyzing systems of equations
Introduction
The purpose of this chapter is to present some tools enabling to analyze system of equations i.e. to get some a-priori information on the roots without solving the systems. These tools allows one to determine that there is a unique solution in a given box and provides a mean to calculate it in a safe way. Hence they are essential to provide a guaranteed solution for a system of equations.Note that a generic analyzer based on the ALIAS parser has been developed and will be presented in the chapter devoted to the parser. This generic analyzer enable to analyze almost any type of system in which at least one equation is algebraic in at least one of the unknowns.
Moore theorem
Mathematical background
Let a system ofand let
then there is a unique solution [16] of
Implementation
The previous test is implemented for
![]() and
and
![]() .
The procedure is implemented as:
.
The procedure is implemented as:
int Krawczyk_Analyzer(int m,int n,
INTERVAL_VECTOR (* IntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* J)(int, int, INTERVAL_VECTOR &),INTERVAL_VECTOR &Input)
with
- m: the number of unknown
- n: the number of equations
- IntervalFunction: a function which return the interval vector evaluation of the equations, see note 2.3.4.3
- J: a function which calculate an interval evaluation of the elements of the jacobian of the equations, see note 2.4.2.2
- Input: the ranges for the variables
Kantorovitch theorem
Mathematical background
Let a system ofeach
- the Jacobian matrix of the system has an inverse
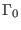 at
at 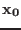 such that
such that
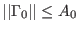
-
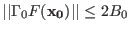
-
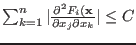 for
for
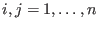 and
and 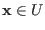
- the constants
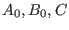 satisfy
satisfy
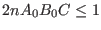
Implementation
int Kantorovitch(int m,VECTOR (* TheFunction)(VECTOR &),MATRIX (* Gradient)(VECTOR &),
INTERVAL_MATRIX (* Hessian)(int, int, INTERVAL_VECTOR &),VECTOR &Input,double *eps)
- m: number of variables and unknowns
- TheFunction: a procedure to compute the value of the equations for given values of the unknowns. This procedure has one arguments which is the value of the unknowns in vector form
- Gradient: a procedure to compute the Jacobian matrix of the system in matrix form. This procedure has one arguments which is the value of the unknowns in vector form
- Hessian: a procedure to compute the Hessian for the equation for interval value input. This procedure compute the m X n, n Hessian matrix in interval matrix form.This procedure has 3 arguments l1,l2,X. The function should return the value of the Hessian of the equations from l1 to l2 The Hessian of the first equation is stored in hess(1..n,1...n), the Hessian of the second equation in hess(n+1..2n,1..n) and so on
- Input: the value of the variables which constitute the center of the convergence ball
int Kantorovitch(int m,
INTERVAL_VECTOR (* TheIntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Gradient)(int, int, INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Hessian)(int, int, INTERVAL_VECTOR &), VECTOR &Input,double *eps)
There is also an implementation of Kantorovitch theorem for univariate
polynomial, see section 5.2.12.
Return code
This procedure return an integer = -1: the Jacobian matrix has no inverse at the mid-point of
Input
= -1: the Jacobian matrix has no inverse at the mid-point of
Input
 =0: the procedure has failed to determine a convergence ball
centered at Input
=0: the procedure has failed to determine a convergence ball
centered at Input
 =1: the procedure has found that an unique solution exist
within the interval [Input-eps,Input+eps]
=1: the procedure has found that an unique solution exist
within the interval [Input-eps,Input+eps]
Rouche theorem
Mathematical background
Let a system ofWe will denote by
and
The most difficult part for using this theorem is to determine
![]() . For algebraic equations it is easy to determine a value
. For algebraic equations it is easy to determine a value
![]() , that we will call the order of Rouche theorem, such that
, that we will call the order of Rouche theorem, such that
![]() and consequently
and consequently ![]() may be
obtained by computing
may be
obtained by computing
for all
For non algebraic finding ![]() requires an analysis of the system.
requires an analysis of the system.
Rouche theorem may be more efficient than Moore or Kantorovitvh theorems. For example when combined with a polynomial deflation (see section 5.9.6) it allows one to solve Wilkinson polynomial of order up to 18 with the C++ arithmetic on a PC, while stand solving procedure fails for order 13.
Implementation
Rouche theorem is implemented in the following way:
- Rouche theorem is checked with respect to the mid-point of a box
- if Roucche theorem is satisfied, then a limited number of Newton iteration is performed to check if Newton indeed converge. If this is the case a ball that include a single solution has been determined
- if a ball has been determined, then, optionaly an inflation procedure )see section 3.1.6) is used to try to enlarge the ball
int Rouche(int DimensionEq,int DimVar,int order,
INTERVAL_VECTOR (* TheIntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_VECTOR (* Jacobian)(int, int, INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Gradient)(int, int, INTERVAL_VECTOR &),
INTERVAL_VECTOR (* OtherDerivatives)(int, int, INTERVAL_VECTOR &),
double Accuracy,
int MaxIter,
INTERVAL_VECTOR &Input,
INTERVAL_VECTOR &UnicityBox)
where
- DimensionEq: number of equations
- DimVar: number of variables
- order: the order for Rouche theorem minus 1
- TheIntervalFunction: a procedure in MakeF format for computing an interval evaluation of the equations
- Jacobian: a procedure in MakeF format that computes the jacobian row by row
- Gradient: a procedure that compute the jacobian in MakeJ format
- OtherDerivatives: a procedure in MakeF format that computes
the derivative of order larger or equal to 2, row by row. This
procedure returns an interval vector of dimension
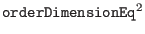
If a ball with a single solution has been found it will be returned in UnicityBox and the procedure returns 1, otherwise it returns 0.
If the flag ALIAS_Always_Use_Inflation is set to 1, then an inflation procedure is used to try to enlarge the box up to the accuracy ALIAS_Eps_Inflation.
Interval Newton
The classical interval Newton method is embedded in the procedure
GradientSolve and HessianSolve but may also be useful in
other procedures. Furthermore this method relies on the use of the
product
![]() where
where ![]() is the Jacobian of the system of
equations and
is the Jacobian of the system of
equations and ![]() the inverse of
the inverse of ![]() computed at some
particular point
computed at some
particular point ![]() . In the classical method this product is
cimputed numerically and this does not take into account that the
element of
. In the classical method this product is
cimputed numerically and this does not take into account that the
element of ![]() are functions of the same parameters. For example if the first column of
are functions of the same parameters. For example if the first column of
![]() is
is ![]() where
where ![]() is some parameter with interval value, the
first element of
is some parameter with interval value, the
first element of
![]() will be computer as
will be computer as
where
The procedure IntervalNewton is a sophisticated interval Newton
algorithm that allows one to introduce knowledge on the product
![]() in the classical scheme. Its syntax is:
in the classical scheme. Its syntax is:
int IntervalNewton(int Dim,INTERVAL_VECTOR &P,INTERVAL_VECTOR &FDIM,
INTERVAL_MATRIX &Grad,MATRIX &GradMid,
MATRIX &InvGradMid,
int hasBGrad,
INTERVAL_VECTOR (* BgradFunc)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* BgradJFunc)(int, int,INTERVAL_VECTOR &),
int grad1,
int grad3B1)
where
- Dim: the size of the system
- P: an interval vector that describes the range for the unknowns
- FDIM: interval value of the equation at the mid-point of P
- Grad: interval jacobian at P
- GradMid: jacobian at the mid-point of P
- hasBgrad: a flag that indicates how
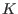 will be
calculated:
will be
calculated:
- 0:
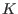 will be calculated numerically
will be calculated numerically
- 1:
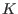 will be calculated using the procedure BgradFunc
will be calculated using the procedure BgradFunc
- 2:
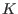 will be calculated using the procedure BgradFunc and the derivatives of the elements of
will be calculated using the procedure BgradFunc and the derivatives of the elements of 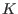 available
through the procedure BgradJFunc
available
through the procedure BgradJFunc
- 0:
- BgradFunc: a user-provided procedure in MakeF format that calculate the
element of
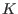 , row by row
, row by row
- BgradJFunc: a user-provided procedure in MakeJ
format that calculate the
derivatives of the elements of
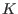
- grad1: if hasBgrad is 1 or 2 we use the procedure
BgradFunc to evaluate
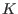 when we are in the 3B filter if grad1 is set to 1. If set to 0 we use BgradFunc only when
dealing with the full box
when we are in the 3B filter if grad1 is set to 1. If set to 0 we use BgradFunc only when
dealing with the full box
- grad3B1: if 1 we use the procedure that evaluates
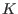 through BgradFunc even if we are in the 3B case. If 2 we use both BgradFunc and
BgradJFunc
through BgradFunc even if we are in the 3B case. If 2 we use both BgradFunc and
BgradJFunc
Various variants of IntervalNewton are available:
int IntervalNewton(int Dim,INTERVAL_VECTOR &P,INTERVAL_VECTOR &FMID,
INTERVAL_MATRIX &Grad,MATRIX &GradMid,MATRIX &InvGradMid)
is the classical interval Newton method with hasBgrad=grad1=grad3B1=0.
int IntervalNewton(int Dim,INTERVAL_VECTOR &P,int DimVar,int DimEq,
int TypeGradMid,MATRIX &InvGradMid,
INTERVAL_VECTOR (*TheIntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Gradient)(int, int, INTERVAL_VECTOR &))
is also the classical interval Newton method for a system having DimVar unknowns and DimEq equations (here DimVar and DimEq are not required to have the same value: only the Dim
first equations will be considered). The flag TypeGradMid is
used to determine how the mid jacobian matrix is calculated: if 0 this
matrix is calculated for the mid-point of P, if 1 the
mid-jacobian is calculated as the mid-matrix of the interval jacobian
calculated for P.
int IntervalNewton(int Dim,INTERVAL_VECTOR &P,int DimEq,int DimVar,
int has_BGrad,
INTERVAL_VECTOR (* BgradFunc)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* BgradJFunc)(int, int,INTERVAL_VECTOR &),
int grad1,int grad3B1,
int TypeGradMid,
MATRIX &GradFuncMid,
MATRIX &InvGradFuncMid,
INTERVAL_VECTOR (* TheIntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Gradient)(int, int, INTERVAL_VECTOR &))
Here the the mid jacobian GradFuncMid and its inverse InvGradFuncMid
will be provided by the procedure.
Miranda theorem
Miranda theorem provides a simple way to determine if there is one, or more, solution of a system of equations in a given box. It has the advantage of not requiring the derivatives of the equations but the drawback of not provinding the proof of the existence of a single solution in the box.
Mathematical background
Let a system ![]() with
with
![]() . Let us consider a
ball
. Let us consider a
ball
![]() for
for ![]() and define
and define
![\begin{eqnarray*}
&&[X]_j^+ = \{X \in {\cal B} {\rm such that} x_j=\overline{x_j...
..._j^- = \{X \in {\cal B} {\rm such that} x_j=\underline{x_j}\}\\
\end{eqnarray*}](img457.png)
for
or if
then
Implementation
The simplest implementation of the Miranda theorem is
int Miranda(int Dim,INTERVAL_VECTOR (* F)(int,int,INTERVAL_VECTOR &),
INTERVAL_VECTOR &Input)
where Dim is the number of equations, Input is a ball for
the variables and F is a procedure in MakeF format that
allows to compute an interval evaluation of the equations. This
procedure returns 1 if Miranda theorem is satisfied for Input, 0
otherwise.
This implementation is embedded in the Solve_General_Interval
solving algorithm.
Another implementation uses the derivatives for improving the interval evaluation:
\begin{verbatim}
int Miranda(int Dim,
INTERVAL_VECTOR (* F)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* J)(int,int,INTERVAL_VECTOR &),
INTERVAL_VECTOR &Input)
J is a procedure in MakeJ format that allows to compute
the derivative of the equations.
Inflation
Mathematical background
Let a system ![]() ,
, ![]() the Jacobian matrix of this system and
the Jacobian matrix of this system and ![]() a solution of the system.
The purpose of the
inflation method is to build a box that will contain only this solution.
Let
a solution of the system.
The purpose of the
inflation method is to build a box that will contain only this solution.
Let ![]() be a ball centered at
be a ball centered at ![]() : if for
any point in
: if for
any point in ![]()
![]() is not singular, then the ball contains only one
solution of the system.
is not singular, then the ball contains only one
solution of the system.
The problem now is to determine a ball such for any point in the ball
the Jacobian is regular. Let ![]() be the matrix
be the matrix
![]() whose
components are intervals. Let
whose
components are intervals. Let ![]() be the diagonal element of H having
the lowest absolute value, let
be the diagonal element of H having
the lowest absolute value, let ![]() be the maximum of the absolute
value of the sum of the elements at row
be the maximum of the absolute
value of the sum of the elements at row ![]() of
of ![]() , discarding the
diagonal element of the row and let
, discarding the
diagonal element of the row and let ![]() be the maximum of the
be the maximum of the
![]() 's. If
's. If ![]() , then the matrix is denoted diagonally dominant
and all the matrices
, then the matrix is denoted diagonally dominant
and all the matrices ![]() are regular [19].
are regular [19].
Let ![]() be a small constant: we will build incrementally the
ball
be a small constant: we will build incrementally the
ball ![]() by using an iterative scheme
defined as:
by using an iterative scheme
defined as:
![\begin{eqnarray*}
&&B_0=X0\\
&&B_n=[B_{n-1}-\epsilon,B_{n-1}+\epsilon]
\end{eqnarray*}](img470.png)
that will be repeated until
Implementation
int ALIAS_Epsilon_Inflation(int Dimension,int Dimension_Eq,
INTERVAL_VECTOR (* TheIntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Gradient)(int, int, INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Hessian)(int, int, INTERVAL_VECTOR &),
VECTOR &X0,
INTERVAL_VECTOR &B)
Note that the Hessian argument is not used in this procedure.
This routine will return 1 if the inflation has succeeded. The value
of