- Definition of a minimum and a maximum
- Methods
- Implementation
- Optimization with function evaluation
- Optimization with function and jacobian evaluation
- Return code
- Order
- The variable table
- Examples
Optimization
ALIAS is also able to deal with optimization problem. Let
consider a scalar function
Definition of a minimum and a maximum
As interval coefficients may appear in the function ![]() we have to
define what will be called a minimum or a maximum of
we have to
define what will be called a minimum or a maximum of ![]() . First we
assume that there is no interval coefficients in
. First we
assume that there is no interval coefficients in ![]() and denote by
and denote by
![]() the minimal or maximal value of
the minimal or maximal value of ![]() over a set of ranges defined
for
over a set of ranges defined
for ![]() and an accuracy
and an accuracy ![]() with which we want to determine
the extremum. The algorithm will return an interval
with which we want to determine
the extremum. The algorithm will return an interval ![]() as an approximation of
as an approximation of ![]() such that
for a minimization problem
such that
for a minimization problem
![]() and
for a maximization problem
and
for a maximization problem
![]() . The
algorithm will also return a value
. The
algorithm will also return a value ![]() for
for ![]() where the extremum
occurs. If we deal with a constrained optimization problem we will
have:
where the extremum
occurs. If we deal with a constrained optimization problem we will
have:
-
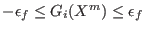
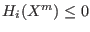 or
or
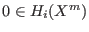 and
and
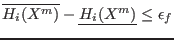
-
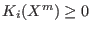
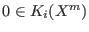 and
and
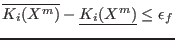
If there are interval coefficients in the optimum function there is
not a unique ![]() but according to the value of the coefficient a
minimal extremum value
but according to the value of the coefficient a
minimal extremum value ![]() and a maximal extremum value
and a maximal extremum value
![]() . The algorithm will return in the lower bound of
. The algorithm will return in the lower bound of ![]() an
approximation of
an
approximation of ![]() and in the upper bound of
and in the upper bound of ![]() an
approximation of
an
approximation of ![]() which verify for a minimization problem:
which verify for a minimization problem:
If the optimum function has no interval coefficients the algorithm
may return no solution if the interval evaluation of the optimum
function has a width larger than ![]() . Evidently the algorithm
will also return no solution if there is no solution that satisfy all
the constraints.
. Evidently the algorithm
will also return no solution if there is no solution that satisfy all
the constraints.
Methods
A first method to find all the solutions of an optimum problem is to consider the system of derivative equations and find its root (eventually under the given constraints): this may be done with the solving procedures described in a previous chapter. Hence we have implemented an alternative method which is able to work even if the optimum function has, globally or locally, no derivatives. This method is implemented as a special case of the general solving procedures. The only difference is that the procedure maintains a value for the current optimum: during the bisection process we evaluate the optimum function for each new box and reject those that are not compatible with the current optimum.Two types of method enable to solve an optimization problem:
- a method which need only a procedure for evaluating
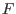 ,
,
- a method which need a procedure for evaluating
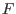 and a
procedure for evaluating its gradient,
and a
procedure for evaluating its gradient,
For the first method
we update the current optimum by computing the optimum
function value at the middle point of the box. For the
method with the gradient a local optimizer based on the steepest
descent
method is also used if there is
only one equation to be minimized or if there are only inequalities
constraints. The local optimizer works in 2 steps: first a rough
optimization and then a more elaborate procedure if the result of the
first step is better than a fixed threshold defined by the global
variable ALIAS_Threshold_Optimiser
whose default value is 100.
Additionally if an extremum ![]() has been already determined
the local optimizer (which may computer intensive)
is called only if the function value
has been already determined
the local optimizer (which may computer intensive)
is called only if the function value ![]() at the middle
point is such that for a maximum
at the middle
point is such that for a maximum
![]() and
and
![]() for a minimum, where ALIAS_LO_A and ALIAS_LO_B are global variables with default
value 0.9 and 1.1.
for a minimum, where ALIAS_LO_A and ALIAS_LO_B are global variables with default
value 0.9 and 1.1.
Implementation
Preliminary notes:
- for both procedures
you may set the global variable
ALIAS_Has_Optimum
to
1 to indicate that you have already determined a possible optimum
value.
This value has to be given in the
global interval variable
ALIAS_Optimum.
Note that this variable is used to store the minimum or the maximum of
the function to be minimized or maximized.
If no a-priori information on the extremum has been given
ALIAS_Has_Optimum will be set to 1 as soon as the algorithm
has a current estimation of the extremum.
If both the minimum and
maximum are looked for, then this variable will be used to store the
minimum while ALIAS_Optimum_Max will be used to store the
maximum.
If you have indicated an a-priori estimation of the extremum it may
happen that the algorithm is unable to find a better extremum. In that
case the global
variables
ALIAS_Algo_Optimum,
ALIAS_Algo_Optimum_Max
will be set to the extremum find by the algorithm (hence if no
a-priori information has been given ALIAS_Algo_Optimum
and ALIAS_Optimum will be the same).
The flag ALIAS_Algo_Has_Optimum will be set to 1 as soon as
the algorithm
has a current estimation of the extremum (which may be worse than the
optimum given a priori).
If the algorithm find a better optimum than the optimum given a priori
the flag ALIAS_Algo_Find_Optimum will be set to 1.
The location of the minimum and maximum can be found in the interval matrix ALIAS_Vector_Optimum, the first line indicating the location of the minimum.
- the flag ALIAS_Optimize is used to indicate which type of optimum you are looking for: -1 for a minimum, 1 for a maximum and 10 for both. This flag is automatically set by the optimization procedures
- the accuracy with which the optimum will be computed is
available in the global variable
ALIAS_Accuracy_Extremum - the function number of the expression to be optimized is available in the global variable ALIAS_Opt_Func
- you may follow the progress of the optimization process by setting the debug flag to at least 1 and setting the flag ALIAS_Allow_Storage to 1. In that case each time the algorithm find a better approximation than the current one he will write down the new value in the file ALIAS_Allow_Storage_File (whose default name is .opti)
- you may also use these procedures just to test if a given function has a minimum lower or a maximum greater than a given value. If you set the flag ALIAS_Stop to 1 and the double ALIAS_Extremum to the desired value the optimization procedure will return as soon as a better minimum or maximum is found. Note that the optimization procedure always reset ALIAS_Stop to 0.
- these procedures are only a specific cases of the general solving procedures: hence the computation time may be largely influenced by the bisection mode
- another factor which may be of importance for the efficiency is
the storage mode. We have seen that two storage modes are
available in ALIAS: the direct or reverse modes. The underlying
principle in the interval analysis method is to examine the leaves of a
tree, the terminal leaves satisfying a decision criteria: either they
are a solution of the problem or not. In the reverse storage mode we
follow all the branches starting from a certain leave until we reach
all the terminal leaves of obtained from this leave while in the
direct storage mode we skip from one branch to another. This mode has
the drawback of an exponential growth in the needed storage while the
reverse mode has the advantage to go directly to the smallest leaves
that may be deleted, thereby freeing storage space.
When solving a system the tree
is static i.e. we can construct it (this is what the algorithm
is doing) and we explore all the leaves. In an optimization problem
the tree is dynamic: as soon as the exploration of a leave
enable to update the current estimation of the extremum we in fact all
the branches of the tree that cannot lead to an improvement of the
extremum. In other words it is important to determine as quickly as
possible the best estimation. In an optimization problem we cannot
determine beforehand the branches that has to be followed for finding
the leaves which is the solution. Thereby the reverse mode has the
drawback that if we are following the wrong branches we will never
eliminate branches and we will explore a large number of leaves that
may have been avoided. With the direct mode we skip from one branch to
another and thus we have a good probability of updating quickly the
extremum. It will therefore be of good policy to use the
direct mode but we then have to deal with the problem of storage. A
mixed strategy can be used: we start with the direct mode and as soon
as we expect a storage problem we switch to the reverse mode. This may
be done by using the flag
Switch_Reverse_Storage
to a value
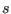 larger than 1: in that case as soon as the number of stored
unexplored boxes exceed
larger than 1: in that case as soon as the number of stored
unexplored boxes exceed 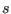 the algorithm will switch to the reverse
mode. The value of
the algorithm will switch to the reverse
mode. The value of 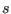 may, for example, be chosen as half the number
of storage space that is allocated. In this optimization mode we may
also use a mixed strategy between the direct and reverse storage mode:
if the flag Reverse_Storage is set to
may, for example, be chosen as half the number
of storage space that is allocated. In this optimization mode we may
also use a mixed strategy between the direct and reverse storage mode:
if the flag Reverse_Storage is set to  , then if the
bisection of the current box leads to
, then if the
bisection of the current box leads to 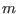 new boxes, the
new boxes, the 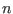 first boxes (as ordered using the ordering described in the
Order section) are stored in the list starting at the current
position of the list, while the
first boxes (as ordered using the ordering described in the
Order section) are stored in the list starting at the current
position of the list, while the 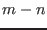 remaining boxes are
stored at the end of the list. Thus setting
remaining boxes are
stored at the end of the list. Thus setting 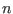 to 1 is equivalent to
using the direct storage mode, while, if we have
to 1 is equivalent to
using the direct storage mode, while, if we have 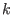 unknowns, setting
unknowns, setting
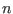 to a value greater than
to a value greater than 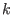 is equivalent to using the reverse
storage mode.
is equivalent to using the reverse
storage mode.
- if you use a mixed bisection mode there is a convenient way to indicate some dependencies between the variable, see the note 8.3.5
- the 2B method (see section 2.17) may be used to improve the efficiency of the optimization algorithms. The ALIAS-Maple procedures HullIConsistency, HullConsistency implement the 2B method and allows to deal with an equation or an inequality that involves the current optimum.
Optimization with function evaluation
The optimization method is implemented as:
int Minimize_Maximize(int m,int n,
INTEGER_VECTOR &Type_Eq,
INTERVAL_VECTOR (* TheIntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_VECTOR & TheDomain,
int Iteration,int Order,
double epsilon,double epsilonf,double epsilone,
int Func_Has_Interval,
INTERVAL Optimum,
INTERVAL_MATRIX & Solution,
int (* Simp_Proc)(INTERVAL_VECTOR &));
the arguments being:
- m: number of unknowns
- n: number of equations, see the note 2.3.4.1
- Type_Eq: type of the equations:
- Type_Eq(i)=-1 if equation i is a constraint
equation of type
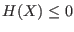
- Type_Eq(i)=0 if equation i is a constraint
equation of type
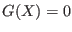
- Type_Eq(i)=1 if equation i is a constraint
equation of type
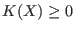
- Type_Eq(i)=-2 if equation i is the optimum function to be minimized
- Type_Eq(i)=2 if equation i is the optimum function to be maximized
- Type_Eq(i)=10 if equation i is the optimum function for which is sought the minimum and maximum
- Type_Eq(i)=-1 if equation i is a constraint
equation of type
- IntervalFunction: a function which return the interval vector evaluation of the equations, see the note 2.3.4.3. This function must be written in a similar manner than for the general solving procedures. Note also that a convenient way to write the IntervalFunction procedure is to use the possibilities offered by the ALIAS-Maple (see the ALIAS-Maple manual).
- TheDomain: box in which we are looking for the extremum of the optimum function
- Iteration: the number of boxes that may be stored
- Order: a flag describing which order is used to store the new boxes, see the note 8.3.4
- epsilon: the maximal width of the solution intervals but not used. Should be set to 0.
- epsilonf: the maximal error for the equality
constraints. If the
problem has constraint of type
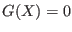 then a solution will verify
then a solution will verify
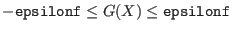
- epsilone: the maximal error on the extremum value.
If the extremum of the function is
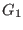 and the procedure
returns the value
and the procedure
returns the value 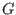 , then a minimum will verify
, then a minimum will verify
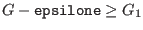 and a maximum
and a maximum
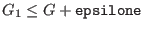 .
.
- Func_Has_Interval: 1 if the optimum function has interval coefficients, 0 otherwise
- Optimum: an interval which contain the extremum value of the optimum function
- Solution: an interval matrix of size at least (2,m)
which will contained the values of
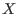 for which the extremum are
obtained
for which the extremum are
obtained
- Simp_Proc: an optional parameter which is a
simplification
procedure that may be provided by the user. It takes as input a box
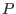 and may:
and may:
- either returns in
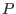 a box with lower width than the initial
a box with lower width than the initial
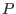 and a return code 0 or 1
and a return code 0 or 1
- or indicates that there is no solution to the optimization problem in the current box, in which case the procedure returns -1
- either returns in
Remember that you may use the 3B method to improve the efficiency of this algorithm (see section 2.3.2) if you have constraint equations.
In some cases it may be interesting to determine if the minimum and maximum have same sign. This may be done by setting the flag ALIAS_Stop_Sign_Extremum either to:
- 1: the procedure will return immediately as soon as it is proven that the extremum will have opposite sign i.e. as soon as two points lead to opposite value for the function. But if the extremum have identical sign the minimum and maximum will be computed up to the accuracy epsilone
- 2: the procedure will return immediately as soon as it is proven that the extremum will have opposite sign i.e. as soon as two points lead to opposite value for the function. If the extremum have same sign the values returned by the procedure are not the minimum and maximum of the function
Return code
The procedure will return an integerSolve_General_Interval except for:
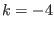 : one of the equation in the system has not a type 0, -1,
-2, 2, 10
or 1 (i.e. it's not an equation or an optimum function,
neither inequality
: one of the equation in the system has not a type 0, -1,
-2, 2, 10
or 1 (i.e. it's not an equation or an optimum function,
neither inequality 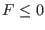 or an
inequality
or an
inequality 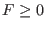 )
)
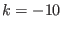 : there is no optimum function i.e. no equation has type
2 or -2 or 10
: there is no optimum function i.e. no equation has type
2 or -2 or 10
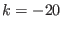 : there is more than one optimum function i.e. more than
one equation has type 2 or -2 or 10
: there is more than one optimum function i.e. more than
one equation has type 2 or -2 or 10
Dealing with inequalities on the same function
In this version of ALIAS there is no direct way to deal with inequalities that are valid for the same function (e.g.- if
this interval is strictly included in
![$[\alpha,\beta]$](img741.png) substitute the interval of
substitute the interval of 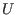 by the value -1 (or any negative number)
by the value -1 (or any negative number)
- if this interval has no intersection with
![$[\alpha,\beta]$](img741.png) substitute the interval of
substitute the interval of 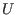 by the value 1 (or any positive number)
by the value 1 (or any positive number)
- if this interval has an intersection with
![$[\alpha,\beta]$](img741.png) but
is not strictly included in it, then
substitute the interval of
but
is not strictly included in it, then
substitute the interval of 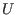 by the interval [-1,1]
by the interval [-1,1]
Optimization with function and jacobian evaluation
The optimization method is implemented as:
int Minimize_Maximize_Gradient(int m,int n,
INTEGER_VECTOR &Type_Eq,
INTERVAL_VECTOR (* TheIntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Gradient)(int, int,INTERVAL_VECTOR &),
INTERVAL_VECTOR & TheDomain,
int Iteration,int Order,
double epsilon,double epsilonf,double epsilone,
int Func_Has_Interval,
INTERVAL Optimum,
INTERVAL_MATRIX & Solution,
int (* Simp_Proc)(INTERVAL_VECTOR &));
the arguments being:
- m: number of unknowns
- n: number of equations, see the note 2.3.4.1
- Type_Eq: type of the equations:
- Type_Eq(i)=-1 if equation i is a constraint
equation of type
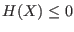
- Type_Eq(i)=0 if equation i is a constraint
equation of type
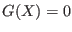
- Type_Eq(i)=1 if equation i is a constraint
equation of type
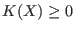
- Type_Eq(i)=-2 if equation i is the optimum function to be minimized
- Type_Eq(i)=2 if equation i is the optimum function to be maximized
- Type_Eq(i)=10 if equation i is the optimum function for which is sought the minimum and maximum
- Type_Eq(i)=-1 if equation i is a constraint
equation of type
- IntervalFunction: a function which return the interval vector evaluation of the equations, see the note 2.3.4.3. This function must be written in a similar manner than for the general solving procedures.
- Gradient: a function which return the interval evaluation of the gradient of the equations, see the note 2.4.2.2. This function must be written in a similar manner than for the general solving procedures with the additional constraint that the function to be minimized of maximized must be the last one.
- TheDomain: box in which we are looking for the extremum of the optimum function
- Iteration: the number of boxes that may be stored
- Order: a flag describing which order is used to store the new boxes, see the note 8.3.4
- epsilon: the maximal width of the solution intervals but not used. Should be set to 0.
- epsilonf: the maximal error for the equality
constraints. If the
problem has constraint of type
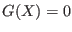 then a solution will verify
then a solution will verify
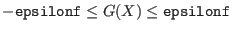
- epsilone: the maximal error on the extremum value.
If the extremum of the function is
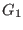 and the procedure
returns the value
and the procedure
returns the value 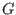 , then a minimum will verify
, then a minimum will verify
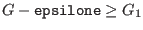 and a maximum
and a maximum
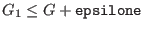 .
.
- Func_Has_Interval: 1 if the optimum function has interval coefficients, 0 otherwise
- Optimum: an interval which contain the extremum value of the optimum function
- Solution: an interval matrix of size at least (2,m)
which will contained the values of
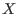 for which the extremum are
obtained
for which the extremum are
obtained
- Simp_Proc: an optional parameter which is a
simplification
procedure that may be provided by the user. It takes as input a box
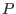 and may:
and may:
- either returns in
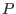 a box with lower width than the initial
a box with lower width than the initial
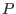 and a return code 0 or 1
and a return code 0 or 1
- or indicates that there is no solution to the optimization problem in the current box, in which case the procedure returns -1
- either returns in
Remember that you may use the 3B method to improve the efficiency of this algorithm (see section 2.3.2).
Note also that a convenient way to write the IntervalFunction and Gradient procedures is to use the possibilities offered by ALIAS-Maple (see the ALIAS-Maple manual).
Return code
The procedure will return an integerSolve_General_Gradient_Interval except for:
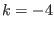 : one of the equation in the system has not a type 0, -1,
-2, 2, 10
or 1 (i.e. it's not an equation or an optimum function,
neither inequality
: one of the equation in the system has not a type 0, -1,
-2, 2, 10
or 1 (i.e. it's not an equation or an optimum function,
neither inequality 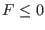 or an
inequality
or an
inequality 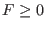 )
)
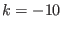 : there is no optimum function i.e. no equation has type
2 or -2 or 10
: there is no optimum function i.e. no equation has type
2 or -2 or 10
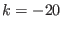 : there is more than one optimum function i.e. more than
one equation has type 2 or -2 or 10
: there is more than one optimum function i.e. more than
one equation has type 2 or -2 or 10
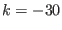 : the last function is not the one to be minimized or maximized
: the last function is not the one to be minimized or maximized
Order
General principle
During the bisection process new boxes will be created and stored in the list. But we want to order these new boxes so that the procedure will consider first the most promising box. The ordering is based on an evaluation index, the new boxes being stored using an increasing order of the index (the box with the lowest index will be stored first). The flag Order indicate which index is used: indexMAXCONSTRAINTFUNCTION@MAX_CONSTRAINT_FUNCTION
- MAX_FUNCTION_ORDER: let
![$[\underline{F_i},\overline{F_i}]$](img743.png) be the interval evaluation of
the optimum equation
be the interval evaluation of
the optimum equation 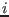 . The index is obtained as
. The index is obtained as
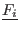 for a minimization problem
and
for a minimization problem
and
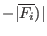 for a maximization problem,
for a maximization problem,
- MAX_CONSTRAINT_FUNCTION: same than MAX_FUNCTION_ORDER if there is only one equation in the system.
Otherwise:
- if there are equality constraints use the MAX_FUNCTION_ORDER index
- if there are only inequality constraints and if they all hold for all the new boxes, then the index is the lower bound of the optimum function for a minimization problem and the upper bound for a maximization problem.
- if there are only inequality constraints and none of the
new boxes satisfied them all: the index is the upper bound
of the inequality for the constraint of type
 and the absolute
value of the lower bound for the constraint of type
and the absolute
value of the lower bound for the constraint of type 
- if there are only inequality constraints and they are all verified only for some of the new boxes, then the index will be calculated in such way that the boxes satisfying the constraints will be stored first according to the value of the lower or upper bound of the optimum function. Then will be stored the boxes not satisfying the constraints according to the index described in the previous item
- MAX_MIDDLE_FUNCTION_ORDER: let
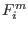 be the value of
the function
be the value of
the function 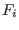 computed for the middle point of the box.
The index is the absolute value of
computed for the middle point of the box.
The index is the absolute value of 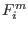
The variable table
Assume now that you have chosen a mixed bisection in which the
bisection is applied on ![]() variables. The procedure will choose the
bisected variables using, for example, the smear function. But in some
cases it may be interesting to guide the bisection: for example if we
know that subsets of the variables have a strong influence
on the extremal value of the
optimum function it may be interesting to indicate that as soon as the
smear function has led to bisecting one variable in a given subset it
may be good to bisect also the other variables in the subset. For
example consider the following functions:
variables. The procedure will choose the
bisected variables using, for example, the smear function. But in some
cases it may be interesting to guide the bisection: for example if we
know that subsets of the variables have a strong influence
on the extremal value of the
optimum function it may be interesting to indicate that as soon as the
smear function has led to bisecting one variable in a given subset it
may be good to bisect also the other variables in the subset. For
example consider the following functions:
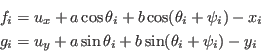
where
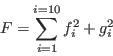
which has 24 unknowns. But clearly each subset
Resize(ALIAS_Bisecting_Table,24,24); Clear(ALIAS_Bisecting_Table); ALIAS_Bisecting_Table(1,2)=1; ALIAS_Bisecting_Table(2,1)=1; ALIAS_Bisecting_Table(3,4)=1; ALIAS_Bisecting_Table(4,3)=1;
Examples
Example 1
Consider the equation:The procedure for the interval evaluation of the 2 functions will be written as:
INTERVAL_VECTOR IntervalTestFunction (int l1,int l2,INTERVAL_VECTOR & in)
// interval valued test function
{
INTERVAL x,y;
INTERVAL_VECTOR xx(2);
x=in(1);
y=in(2);
if(l1==1)
xx(1)=Cos(x)+y*Sqr(Cos(y))-0.2;
if(l1<=2 && l2>=2)
xx(2)=Sqr(x)+Sqr(y);
return xx;
}
while the main program may be written as:
int main()
{
int Iterations, Dimension,Dimension_Eq,Num,i,j,precision;
double Accuracy,Accuracy_Variable;
INTERVAL_MATRIX SolutionList(2,2);
INTERVAL_VECTOR TestDomain(2),F(2),P(2),H(2);
INTEGER_VECTOR Type(2);
INTERVAL Optimum;
REAL pi;
pi=Constant::Pi;
Dimension_Eq=2;Dimension=2;
TestDomain(1)=INTERVAL(-pi,pi);TestDomain(2)=INTERVAL(-pi,pi);
cerr << "Number of iteration = "; cin >> Iterations;
cerr << "Accuracy on Function = "; cin >> Accuracy;
Type(1)=0;Type(2)=-2;
Accuracy=0;
Num=Minimize_Maximize(Dimension,Dimension_Eq,Type,
IntervalTestFunction,TestDomain,Iterations,Accuracy_Variable,
Accuracy,0,Optimum,SolutionList);
if(Num<0)
{
cout << "The procedure has failed, error code:"<<Num<<endl;
return 0;
}
cout<<"Optimum:"<<Optimum<<" obtained at"<<endl;
for(i=1;i<=Num;i++)
{
cout << "x=" << SolutionList(i,1) <<endl;
cout << "y=" << SolutionList(i,2) <<endl;
}
return 0;
}
The Minimize_Maximize
and Minimize_Maximize_Gradient procedures will return the
same numerical results but the number of boxes will change.
The
results obtained for a full bisection,
the MAX_MIDDLE_FUNCTION_ORDER and according to the accuracy epsilonf and the storage mode (either direct (DSM) or reverse (RSM), see section 2.3.1.2) are presented in the following table (the number of boxes for the Minimize_Maximize_Gradient procedure is indicated in parenthesis):
| epsilonf | Minimum | |
|
boxes |
| 0.01, DSM | [1.12195667, 1.12195667] | [-0.944932,-0.4786] | [-0.944932,-0.4786] | 76 (36) |
| 0.01, RSM | [1.12195667, 1.12195667] | [-0.944932,-0.4786] | [-0.944932,-0.4786] | 59 (37) |
| 0.001, DSM | [1.1401661,1.1401661] | [-0.954903,-0.477835] | [-0.954903,-0.477835] | 201 (75) |
| 0.001, RSM | [1.1401661,1.1401661] | [-0.954903,-0.477835] | [-0.954903,-0.477835] | 148 (67) |
| 0.000001, DSM | [1.14223267,1.14223267] | [-0.957596,-0.474596] | [-0.957596,-0.474596] | 5031 (2041) |
| 0.000001, RSM | [1.14223267,1.14223267] | [-0.957596,-0.474596] | [-0.957596,-0.474596] | 4590 (2164) |
Example 2
Consider the problem of finding the coordinates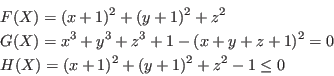
With epsilonf=0.0001 we find out that the point is located at at (-0.747,-0.747,0.086059) which is well inside the sphere and that the minimal distance is 0.13529.
We may also compute the minimal distance not to a point but to a line segment,
for example
defined by
![]() ,
, ![]() ,
, ![]() . In that case the optimum
function in the
evaluation procedure may be defined as:
. In that case the optimum
function in the
evaluation procedure may be defined as:
Sqr(x+INTERVAL(0.9,1.1))+Sqr(y+1)+Sqr(z)and with epsilonf=0.0001 the algorithm will return that the minimal distance lie in the range [0.0907,0.1925].