INRIA home page
Subsections
ALIAS-C++ is a C++ library of algorithms, intended to be run on
PC under Unix or Linux, that deal with problems like
solving systems of equations and
inequalities,optimization, linear algebra 
.
This library is partly interfaced with a Maple
package that allows one to create and run a solver based on the C++ library
within a Maple session. Otherwise in many cases most of the C++ code may
be written
directly by the package, see the ALIAS-Maple manual. The library has
been designed to support a distributed implementation based on the
master-slaves scheme, see the corresponding chapter.
Expressions involved in these problems may be arbitrary combination of
the most classical mathematical
functions (algebraic terms, sine, cosine, log etc..) and whose
coefficients
are real numbers or, in some cases, intervals.
Most algorithms in ALIAS are based on interval analysis and
can be used for almost any system as soon as it is composed of
classical mathematical operators (see section 2.1.1.2 for the
available operators). Some algorithms may be used only for problems with
specific structure such as solving algebraic, linear, distance,
equation systems.
ALIAS may also
deal with functions that involve determinants of matrices, without
having to expand the determinants.
Without being exhaustive you may find in ALIAS algorithms that
enable one to:
- find an approximation of the real roots of 0-dimensional systems
- find an approximation of the variety defined by n-dimensional systems
- find an approximation of
the global minimum or maximum of a function (eventually under
equations and/or inequalities
constraints) up to an accuracy provided by the user
- analyze a system of algebraic equations to determine bounds for
its real roots
- parse a formula file describing a set of functions in order to
compute an interval evaluation of the functions that can be used for
the solving procedures
- check the regularity of an interval matrix
- provide an enclosure of definite integrals
This version of the library has about 88000 lines of C++
code, to which should be added the 13 000 lines for BIAS/Profil/
Most of these algorithms are designed in view of their use in a
parallel implementation (see chapter 13).
This library is one of the main
software development platform of the HEPHAISTOS project.
There are various motivations underlying the development of this
platform:
- interval analysis allows to solve very different problems (not
only solving systems of equations) as soon as the unknowns are
restricted to lie within a given
domain, which is relevant to many applications. The expertise of the
HEPHAISTOS project in application domains such as mechanism theory,
control theory, robotics has allowed us to develop algorithms and test
the library on numerous
realistic problems (historically speaking it was the need of tools to
solve problems in these fields that has led to the development of
ALIAS)
- interval analysis allows to deal with uncertainties that are
present in almost all applications
- interval analysis allows to take into account numerical
round-off errors that may have a very negative impact on the result of
classical numerical analysis algorithms. This allows one to get safe results: whenever an interval-analysis based method will give a
solution then the result is guaranteed. On the other hand such
algorithm may just states that the current problem cannot be solved
with the current computer arithmetics. At the same time
interval-analysis based methods may provide an exact answer in
the sense that it will be possible to get a solution of the problem
wit an arbitrary accuracy in term of number of exact digits for the
solution.
- classical problem solving approaches rely on the transformation
of the initial problem into a solving problem
that have the same solution (or solutions that may be transformed into
the solutions of the initial problem) but which has a structure that
is more appropriate for solving (for example a system of sine and
cosine will be transformed into an algebraic system for which there is
powerful solving methods).
This operation may transform a simple problem into a
much more complex solving problem.
At the opposite interval analysis allows one to focus on the problem to be
solved which will often results in a more efficient strategy
This may also be considered a drawback of interval analysis: very often it
is necessary to think backward and to focus on what is really the
problem to be solved in view of a solving by interval analysis. We
will present some examples of this approach.
- although in many cases other approaches may be used to solve
problems addressed in ALIAS they are very often computer intensive.
A short pre-processing with interval analysis based methods may avoid
using these approaches whenever it is not necessary, therefore
drastically reducing the whole computation time. Furthermore the computation
time of interval analysis based methods will decrease with the
decrease of the search space: hence there will always be a limit on
the search space under which the interval analysis method will be
faster than any other method
- although they are numerous papers and books on interval
analysis
(see [5,6,17,18,20,21,24]
to name a few)
the few implementations that are freely available are far from being
complete. Our purpose is to offer a wide range of algorithms
- various communities are working on interval analysis based
algorithms: constraint programming, operational research, numerical
analysis, Furthermore other communities (such as the
algebraic geometry community) are addressing the same problems. In our
view there is a lack of collaboration
between these communities although basically they intend to solve the
same type of problems and that the different methods are very often
complementary
- the ALIAS-C++ library is partly interfaced with a Maple
package. We strongly believe that symbolic computation, apart for
being very convenient to produce error-free C++ code, will also play
an important role to improve the efficiency of the algorithms. The
ALIAS-Maple manual provides procedures and examples for this increase
in efficiency
- we do not claim that interval analysis is an universal tool:
it may fail to solve
a given problem. It is almost impossible to determine beforehand if
interval-analysis based method will work. One of the purposes of ALIAS is to provide
the necessary
tool to test quickly existing methods. Another purpose is to provide
the basic tools so that new algorithms may be developed
efficiently. On the other hand interval analysis allow to solve
problems for which (to the best of our knowledge) there is no
alternate solution.
- we have sometime heard the somewhat negative
comment that interval analysis is "only" a
version of the branch-and-bound algorithm. Although branch-and-bound
is indeed a key component of the interval analysis algorithm we
strongly believe that classifying the strategy only by this component
is unfair as many other methods are used (and will make a drastic
difference in term of computation time). Furthermore we consider that
methods should also be judged according to what problem they may
solve. In that regard interval analysis is very rich and has proved to
be effective in realistic applications problems for which, to the best
of our knowledge, there was no alternate methods
(chapter 15 will present some of this problems)
ALIAS is partly interfaced with Maple, see the
ALIAS-Maple documentation.
This manual contains the following chapters:
- Chapter 2 is devoted to a brief description of interval analysis and
to the various algorithms of ALIAS enabling to solve systems,
either general purpose solving methods or algorithms for specific type
of
systems (e.g. system with a large number of linear terms or involving
determinant of matrices).
- Chapter 3 deals with the analysis of system of functions
- Chapter 4 deals especially with the analysis of trigonometric
functions
- Chapter 5 describes algorithms for the
analysis of univariate polynomial.
- Chapter 6 is devoted to the study of parametric polynomials and
calculation on the eigenvalues of parametric matrices
- Chapter 7 is devoted to procedure related to linear algebra
- Chapter 8 deals with global optimization problems, constrained or
not.
- In Chapter 9 we describe how ALIAS can be used for dealing
with one-dimensional systems and
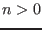dimensional systems
- Chapter 10 is devoted to guaranteed integration procedures
- Chapter 11 describes some miscellaneous ALIAS procedures
- Chapter 12 is devoted to the ALIAS parser and the generic
analyzer and solver based on this parser
- In Chapter 13 we explain
how ALIAS can be used in a parallel implementation
- In Chapter 14 we explain how to use and install ALIAS,
- the examples treated in the various chapters are presented in chapter
12,
- Chapter 15 presents various examples used in this documentation
together with some examples of problems that interval analysis can solve
- Chapter 16 is the troubleshooting chapter, in which is
explained what can go wrong with ALIAS procedures and how to
adjust ALIAS parameters to obtain a better efficiency
This manual is intended to be read by two types of users:
- application oriented
- developer
In the first case you may skip all the "Mathematical background"
sections and go directly to the "Implementation" and "Examples"
sections. In some cases it may be necessary however to consult the
"Mathematical background" section to understand the meaning of some
parameters of the procedure you intend to use.
In the latter case the "Mathematical background" sections
may be of interest.
Next: Solving with Interval Analysis
Up: ALIAS-C++
Previous: ALIAS-C++