- Calculating determinant
- Matrix inverse
- Solving systems of linear equations
- Regularity of parametric interval matrices
- Characteristic polynomial
- Spectral radius
Linear algebra
Calculating determinant
Scalar and interval matrix
The determinant of a scalar matrix may be calculated with the procedure ALIAS_MRINVD that is also used to determine the inverse of the matrix, see section 7.2.
The determinant of an interval matrix may be calculated by using Gaussian elimination with the procedure
int ALIAS_Det_By_Gaussian_Elim(INTERVAL_MATRIX &B, INTERVAL &DET)This procedures returns 1 if the determinant has been successfully calculated and is returned in DET, 0 otherwise.
There are five main procedures to compute an interval evaluation of the determinant of an interval square matrix:
INTERVAL Slow_Determinant(INTERVAL_MATRIX &A) INTERVAL Slow_NonZero_Determinant(INTERVAL_MATRIX &A) INTERVAL Medium_Determinant(INTERVAL_MATRIX &A) INTERVAL Fast_Determinant(INTERVAL_MATRIX &A) INTERVAL VeryFast_Determinant(INTERVAL_MATRIX &A)These procedures differ only by the computation time (large for the Slow procedure as soon as the dimension of the matrix is larger than 5) and the accuracy of the interval evaluation (which is the worst for the Fast procedure). The Medium_Determinant procedure is a good compromise between efficiency and speed. The procedure Slow_NonZero_Determinant is a special occurrence of the procedure Slow_Determinant which will return as soon it has determined that the interval evaluation of the determinant does not include 0. Note that if the flag ALIAS_Use_Gaussian_Elim_In_Det is set to 1 (the default value being 0), then these procedures will also use the Gaussian elimination to improve the evaluation of the determinant.
There are also special version of the previous procedures:
INTERVAL Slow_Determinant22(INTERVAL_MATRIX &A,
INTERVAL (* TheDet22)(INTEGER_VECTOR &,INTEGER_VECTOR &,INTERVAL_VECTOR &),
INTERVAL_VECTOR &Input)
INTERVAL Medium_Determinant22(INTERVAL_MATRIX &A,
INTERVAL (* TheDet22)(INTEGER_VECTOR &,INTEGER_VECTOR &,INTERVAL_VECTOR &),
INTERVAL_VECTOR &Input)
INTERVAL Fast_Determinant22(INTERVAL_MATRIX &A,
INTERVAL (* TheDet22)(INTEGER_VECTOR &,INTEGER_VECTOR &,INTERVAL_VECTOR &),
INTERVAL_VECTOR &Input)
They differ because the calculation of all the dimensions 2 minors
are computed using the TheDet22 procedure.
The syntax of this procedure is:
INTERVAL TheDet22(INTEGER_VECTOR &ROW,INTEGER_VECTOR &COL,INTERVAL_VECTOR &Input)The integer vectors ROW and COL will have all components equal to 0 except for 2 element, which indicate which rows and columns are used to produce the 2
A more general implementation of the previous procedure is
INTERVAL Determinant22(INTERVAL_MATRIX &A,int Minor,int Row,
INTERVAL (* TheDet22)(INTEGER_VECTOR &,INTEGER_VECTOR &,INTERVAL_VECTOR &),
INTERVAL_VECTOR &Input)
In this procedure Minor indicates the size of the minor that can
be computed using the procedure TheDet22 and Row indicates
if an expansion by row (1) or by column (0) is used.
There are also procedures to compute the derivatives of a determinant
INTERVAL Fast_Derivative_Determinant(INTERVAL_MATRIX &A,INTERVAL_MATRIX &AG); INTERVAL Medium_Derivative_Determinant(INTERVAL_MATRIX &A,INTERVAL_MATRIX &AG); INTERVAL Slow_Derivative_Determinant(INTERVAL_MATRIX &A,INTERVAL_MATRIX &AG);A is a matrix that contain the interval evaluation of the component of the matrix and AG is a matrix that contain the interval evaluation of the derivatives of the components of the matrix. In other words if
If a procedure TheDet22 for calculating the minor is available you may use
INTERVAL Derivative_Determinant22(INTERVAL_MATRIX &A,INTERVAL_MATRIX &AG,
int Minor,
INTERVAL (* TheDet22)(INTEGER_VECTOR &,INTEGER_VECTOR &,INTERVAL_VECTOR &),
INTERVAL_VECTOR &Input)
There are also procedures to compute the second order derivatives of a determinant
INTERVAL Fast_Hessian_Determinant(INTERVAL_MATRIX &A,INTERVAL_MATRIX &AG, INTERVAL_MATRIX &AH) INTERVAL Medium_Hessian_Determinant(INTERVAL_MATRIX &A,INTERVAL_MATRIX &AG, INTERVAL_MATRIX &AH) INTERVAL Slow_Hessian_Determinant(INTERVAL_MATRIX &A,INTERVAL_MATRIX &AG, INTERVAL_MATRIX &AH)For a matrix
You may also obtain an upper bound for the determinant of a matrix by using the procedure:
double Hadamard_Determinant(MATRIX &J)where we use the Hadamard bound of the determinant
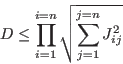
A similar procedure exists for an interval matrix
INTERVAL Hadamard_Determinant(INTERVAL_MATRIX &J)
The determinant of a scalar matrix may be calculated with
double Determinant(MATRIX &J)
Polynomial matrix
A polynomial matrix is assumed is assumed here to be a matrix whose elements are univariate polynomial in the same variable. The determinant of such matrix (which is a polynomial) may be computed with the procedure
int Determinant_Characteristic(POLYNOMIAL_MATRIX A,
INTERVAL_VECTOR &Coeff)
where
- A: a POLYNOMIAL_MATRIX structure which describes
the polynomial matrix. This structure is composed of
- dim: the dimension of the matrix
- Coeff: an interval vector with indicates the coefficients of the polynomial in the matrix, row by row
- Order: an integer matrix. m=Order(i,j)
indicates that the element at the
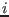 -th row and
-th row and 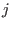 -th column has
coefficients Coeff(l) to Coeff(m) where l is Coeff(i,j-1)+1 if j is greater than 1, Coeff(i-1,dim)
otherwise. Hence Order(1,1)=3 indicate that the first elements
has as coefficient Coeff(1), Coeff(2), Coeff(3) and hence is a
second order polynomial
-th column has
coefficients Coeff(l) to Coeff(m) where l is Coeff(i,j-1)+1 if j is greater than 1, Coeff(i-1,dim)
otherwise. Hence Order(1,1)=3 indicate that the first elements
has as coefficient Coeff(1), Coeff(2), Coeff(3) and hence is a
second order polynomial
- Coeff: the coefficients of the determinant polynomial
Matrix inverse
The inverse of a scalar matrix may be used by using the Inverse function of the BIAS/Profil package or with
void ALIAS_MRINVD(VECTOR &A,VECTOR &B,int N,int *KOD,double *DET,double EPS,
INTEGER_VECTOR &IL,INTEGER_VECTOR &IC)
where
- A is the matrix given by column
- B is the inverse of A
- N is the dimension of the matrix
- KOD is a return code. If KOD is 0 then A is estimated not to have an inverse, otherwise KOD is set to 1
- DET: the determinant of A
- EPS: a threshold, if a pivot has an abolute value less than this value, then it is assumed to be 0
- IL, IC: working table of size N
The inverse of an interval matrix may be defined as the set of matrices corresponding to the inverse of a matrix included in the set defined by the interval matrix. This set cannot usually be computed exactly but a set of matrices guaranteed to include the inverse interval matrix may be computed. The following procedure allows one to compute such overestimation.
int Inverse_Interval_Matrix(int Dim,int cond,INTERVAL_MATRIX &Jac,INTERVAL_MATRIX &InvJac)
where Dim is the dimension of the matrix Jac. The flag cond has to be set to 1 if pre-conditioning is used, 0 otherwise. Pre-conditionning will usually leads to a smaller overestimation but is more computer intensive. This procedures returns 1 if it has been able to compute the inverse, 0 otherwise.
Note that using this procedure should not be used for solving an interval linear system.
Solving systems of linear equations
Mathematical background
Let us assume that we have anwhere the
A classical scheme for finding the enclosure is to use an interval variant of the Gauss elimination scheme [18].
When the unknowns lie in given ranges we may compute an interval
evaluation ![]() of
of ![]() and an interval evaluation
and an interval evaluation
![]() of
of ![]() .
The Gauss elimination scheme may be written as [18]
.
The Gauss elimination scheme may be written as [18]
| (7.2) | |||
| (7.3) |
The enclosure of the variable
| (7.4) |
A drawback of this scheme is that the family of linear systems that
will be obtained for all instances of ![]() is usually a subset of
the family of linear systems defined
by
is usually a subset of
the family of linear systems defined
by ![]() ,
, ![]() , as we do not take into account the
dependency of the elements of
, as we do not take into account the
dependency of the elements of ![]() . Furthermore the
calculation in the scheme involves products, sums and ratio of
elements of
. Furthermore the
calculation in the scheme involves products, sums and ratio of
elements of ![]() and their direct interval evaluation again do
not take into account the dependency between the elements. Hence a
direct application of the Gauss scheme will usually lead to an
overestimation of the enclosure.
and their direct interval evaluation again do
not take into account the dependency between the elements. Hence a
direct application of the Gauss scheme will usually lead to an
overestimation of the enclosure.
A possible method to reduce this overestimation is to consider the
system
where
But even with a possible good ![]() the dependency between the elements
of
the dependency between the elements
of ![]() are not taken into account and hence the
overestimation of the enclosure may be large.
are not taken into account and hence the
overestimation of the enclosure may be large.
A first possible way to reduce this overestimation is to improve the
interval evaluation of ![]() ,
, ![]() by using the
derivatives of their elements with respect to
by using the
derivatives of their elements with respect to ![]() and the procedure described in
section 2.4.2.3. Note that the procedures necessary to compute
the elements of
and the procedure described in
section 2.4.2.3. Note that the procedures necessary to compute
the elements of ![]() ,
, ![]() and their derivatives may
be obtained by using the MakeF, MakeJ procedures of
ALIAS-maple.
and their derivatives may
be obtained by using the MakeF, MakeJ procedures of
ALIAS-maple.
But to improve the efficiency of the procedure it must be noticed that
at iteration ![]() an interval evaluation of the derivatives of
an interval evaluation of the derivatives of ![]() with respect to
with respect to ![]() may be deduced for the derivatives of
the elements computed at iteration
may be deduced for the derivatives of
the elements computed at iteration ![]() . As we have the derivatives
of the elements at iteration 0 we may then deduce the derivatives of
the elements at any iteration and use these derivatives to improve the
interval evaluation of these elements (see sections 2.4.1.1
and 2.4.2.3).
. As we have the derivatives
of the elements at iteration 0 we may then deduce the derivatives of
the elements at any iteration and use these derivatives to improve the
interval evaluation of these elements (see sections 2.4.1.1
and 2.4.2.3).
Implementation
The simplest Gaussian elimination scheme is implemented as:
int Gauss_Elimination(INTERVAL_MATRIX &Ain,
INTERVAL_VECTOR &b,INTERVAL_VECTOR &bout)
where
- Ain: the A interval matrix
- b: the b interval vector
- bout: the enclosure of the set of solutions
This computation for the initial system and a pre-conditioned system has been implemented in the procedure:
int Gauss_Elimination_Derivative(MATRIX &Cond,INTERVAL_MATRIX &Ain,
INTERVAL_MATRIX &ACondin,
const INTERVAL_VECTOR bin,
const INTERVAL_VECTOR bCondin,
INTERVAL_VECTOR &bout,
INTERVAL_VECTOR & Param,
INTERVAL_VECTOR (* Func)(int l1, int l2, INTERVAL_VECTOR & v_IS),
INTERVAL_MATRIX (* JFunc)(int l1, int l2, INTERVAL_VECTOR & v_IS),
INTERVAL_VECTOR (* bFunc)(int l1, int l2, INTERVAL_VECTOR & v_IS),
INTERVAL_MATRIX (* JbFunc)(int l1, int l2, INTERVAL_VECTOR & v_IS))
where
- Cond: the pre-conditioning matrix. If all the elements of Cond are 0 the procedure will implement the Gauss elimination scheme only on the initial system
- Ain: the interval evaluation of the
 matrix
matrix
- ACondin: the interval evaluation of the Cond
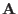 matrix
matrix
- bin: the interval evaluation of
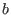
- bCondin: the interval evaluation of Cond
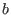
- bout: the enclosure of the interval linear system
- Param: the ranges for
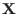
- Func: a procedure that computes the interval evaluation of
the elements of
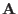 . These elements are stored rows by rows in
an
. These elements are stored rows by rows in
an 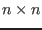 interval vector (see the note 2.3.4.3)
interval vector (see the note 2.3.4.3)
- Jfunc: a procedure that computes the interval evaluation of
the derivatives of the elements of
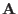 , see the
note 2.4.2.2
, see the
note 2.4.2.2
- bFunc:a procedure that computes the interval evaluation of
the elements of
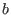 , see the note 2.3.4.3
, see the note 2.3.4.3
- Jbfunc: a procedure that computes the interval evaluation of
the derivatives of the elements of
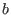 , see the
note 2.4.2.2
, see the
note 2.4.2.2
This procedure will return 1 if the Gauss elimination scheme has been completed, 0 otherwise. It will return in general a much more better enclosure than the classical interval Gauss elimination scheme.
For example consider the system
for
while if we use the derivatives we get
while the solutions are
The ALIAS-Maple procedure LinearBound implements this calculation.
Regularity of parametric interval matrices
A parametric interval matrix is a matrix whose elements are functions of unknowns whose values lie in some pre-defined ranges. It is therefore a matrix that has a higher structure than the classical interval matrix (i.e. matrices whose elements are intervals) as there may be dependency between the elements of the matrix.
A sophisticated procedure to check for the regularity of a parametric matrix is based on the following scheme: the sign of the determinant is calculated for a point value of the input parameters (say positive), then the algorithm try to find another input value such that the sign of the corresponding determinant is negative.
Implementation
int Matrix_Is_Regular(int dimA,
INTERVAL_VECTOR (* Func)(int l1, int l2,INTERVAL_VECTOR & v_IS),
int (* A_Cond)(int dimA,INTERVAL_VECTOR (* Func)(int l1, int l2,INTERVAL_VECTOR & v_IS),INTERVAL_VECTOR & v_IS,INTERVAL_MATRIX &K),
INTERVAL_MATRIX (* A_Cond_Left)(INTERVAL_VECTOR & v_IS_Left),
INTERVAL_MATRIX (* A_Cond_Right)(INTERVAL_VECTOR & v_IS_Right),
INTERVAL Determinant_Matrix(INTERVAL_MATRIX &A,INTERVAL_VECTOR &X),
INTERVAL Determinant_A_Cond_Left(INTERVAL_MATRIX &A,INTERVAL_VECTOR &X),
INTERVAL Determinant_A_Cond_Right(INTERVAL_MATRIX &A,INTERVAL_VECTOR &X),
int Type_Cond,
INTEGER_VECTOR &Type_Determinant,
int Iteration,
INTERVAL_VECTOR &X,
int (* Simp)(int dimA,INTERVAL_MATRIX & Acond,INTERVAL_VECTOR
& v_IS))
where
- dimA: the dimension of the matrix
- Func: a procedure that allows to compute the entries of the matrix, row by row. Func(l1,l2,X) computes the element at row l1, column l2 of the matrix for the input X
- A_Cond: a procedure that compute a conditioning matrix. K. It returns 1 if the conditioning matrix has been calculated, 0 otherwise. You may use the built-in procedure ALIAS_A_Cond_Mid that calculate the scalar matrix for the mid point of the input parameters and returns its inverse. If you don't intend to use conditioning you may use the dummy procedure ALIAS_A_Cond_Void that just returns 0. In that case the procedure that should be used to calculated the conditioned matrix may be ALIAS_Cond_Void
- A_Conf_Left: a procedure to compute the lefts conditioned matrix AK. It takes as input a vector constituted first of the elements of X followed by the elements of K, arranged row by row. If no such procedure is available the dummy procedure ALIAS_A_Cond_Void may be used.
- A_Conf_Right: a procedure to compute the lefts conditioned matrix KA. It takes as input a vector constituted first of the elements of X followed by the elements of K, arranged row by row. If no such procedure is available the dummy procedure ALIAS_A_Cond_Void may be used.
- Type_Cond: indicates how the conditioning is used: 0 if no conditioning is used, 1 if AK is being used, 2 if KA is used and 3 if both AK and KA are used
- Type_Det: an integer of dimension 3 that indicates which procedure is used to calculate the determinant. The value of the integer is 1 for Fast_Determinant, 2 for Medium_Determinant and 3 for Slow_Determinant. The first integer is for A, the second for AK and the third for KA
- Iteration: the maximum number of boxes that will be used by the algorithm
- X: the ranges for the input parameters
- Simp: a user supplied simplification procedure that returns -1 if all the matrices for the input parameter X are regular. If no such procedure is available you may use the dummy procedure ALIAS_Simp_Matrix_Void
The flag Simp_In_Cond may be used to design the simplification
procedure. It is set to 0 when the simplification procedure is used to
check the initial matrix ![]() , to -1 or -2 when testing the regularity of the
conditioning matrix, to 1 when testing the regularity of AK
and to 2 for KA.
, to -1 or -2 when testing the regularity of the
conditioning matrix, to 1 when testing the regularity of AK
and to 2 for KA.
This procedure may also be used with the following syntaxes:
int Matrix_Is_Regular(int dimA,
INTERVAL_VECTOR (* Func)(int l1, int l2,INTERVAL_VECTOR & v_IS),
int (* A_Cond)(int dimA,INTERVAL_VECTOR (* Func)(int l1, int l2,INTERVAL_VECTOR & v_IS),INTERVAL_VECTOR & v_IS,INTERVAL_MATRIX &A),
INTERVAL_MATRIX (* A_Cond_Left)(INTERVAL_VECTOR & v_IS_Left),
INTERVAL_MATRIX (* A_Cond_Right)(INTERVAL_VECTOR & v_IS_Right),
INTERVAL Determinant_Matrix(INTERVAL_MATRIX &A,INTERVAL_VECTOR &X),
INTERVAL Determinant_A_Cond_Left(INTERVAL_MATRIX &A,INTERVAL_VECTOR &X),
INTERVAL Determinant_A_Cond_Right(INTERVAL_MATRIX &A,INTERVAL_VECTOR &X),
int Type_Cond,
INTEGER_VECTOR &Type_Determinant,
int Iteration,
INTERVAL_VECTOR &Domain)
int Matrix_Is_Regular(int dimA,
INTERVAL_VECTOR (* Func)(int l1, int l2,INTERVAL_VECTOR & v_IS),
int (* A_Cond)(int dimA,INTERVAL_VECTOR (* Func)(int l1, int l2,INTERVAL_VECTOR & v_IS),INTERVAL_VECTOR & v_IS,INTERVAL_MATRIX &A),
INTERVAL_MATRIX (* A_Cond_Left)(INTERVAL_VECTOR & v_IS_Left),
INTERVAL_MATRIX (* A_Cond_Right)(INTERVAL_VECTOR & v_IS_Right),
int Type_Cond,
INTEGER_VECTOR &Type_Determinant,
int Iteration,
INTERVAL_VECTOR &Domain,
int (* Simp)(int dimA,INTERVAL_MATRIX & Acond,INTERVAL_VECTOR
& v_IS))
int Matrix_Is_Regular(int dimA,
INTERVAL_VECTOR (* Func)(int l1, int l2,INTERVAL_VECTOR & v_IS),
int Type_Determinant,
int Iteration,
INTERVAL_VECTOR &Domain)
int Matrix_Is_Regular(int dimA,
INTERVAL_VECTOR (* Func)(int l1, int l2,INTERVAL_VECTOR & v_IS),
int Type_Determinant,
int Iteration,
INTERVAL_VECTOR &Domain,
int (* Simp)(int dimA,INTERVAL_MATRIX & Acond,INTERVAL_VECTOR
&v_IS))
int Matrix_Is_Regular(int dimA,
INTERVAL_VECTOR (* Func)(int l1, int l2,INTERVAL_VECTOR & v_IS),
int (* A_Cond)(int dimA,INTERVAL_VECTOR (* Func)(int l1, int l2,INTERVAL_VECTOR & v_IS),INTERVAL_VECTOR & v_IS,INTERVAL_MATRIX &A),
INTERVAL_MATRIX (* A_Cond_Left)(INTERVAL_VECTOR & v_IS_Left),
INTERVAL_MATRIX (* A_Cond_Right)(INTERVAL_VECTOR & v_IS_Right),
int Type_Cond,
INTEGER_VECTOR &Type_Determinant,
int Iteration,
INTERVAL_VECTOR &Domain)
int Matrix_Is_Regular(int dimA,
INTERVAL_VECTOR (* Func)(int l1, int l2,INTERVAL_VECTOR & v_IS),
INTERVAL_MATRIX (* A_Cond_Left)(INTERVAL_VECTOR & v_IS_Left),
INTERVAL_MATRIX (* A_Cond_Right)(INTERVAL_VECTOR & v_IS_Right),
int Type_Cond,
INTEGER_VECTOR &Type_Determinant,
int Iteration,
INTERVAL_VECTOR &Domain)
int Matrix_Is_Regular(int dimA,
INTERVAL_VECTOR (* Func)(int l1, int l2,INTERVAL_VECTOR & v_IS),
INTERVAL_MATRIX (* A_Cond_Left)(INTERVAL_VECTOR & v_IS_Left),
INTERVAL_MATRIX (* A_Cond_Right)(INTERVAL_VECTOR & v_IS_Right),
int Type_Cond,
INTEGER_VECTOR &Type_Determinant,
int Iteration,
INTERVAL_VECTOR &Domain,
int (* Simp)(int dimA,INTERVAL_MATRIX & Acond,INTERVAL_VECTOR
&v_IS))
Note that the 3B method is implemented as a built-in procedure called
ALIAS_3B_Regular_Matrix, but is
usually not very efficient.
Rohn simplification procedure
Mathematical background
LetThe set of matrices
Note than another simplification procedure may be built by using the spectral radius (see section 7.6).
Implementation
Rohn test is implemented as:int Rohn_Consistency(int dimA,INTERVAL_MATRIX &A)the procedure returning -1 if all the matrices in A are regular, 0 otherwise.
To speed up the procedure a remembering mechanism has been implemented. If the flag ALIAS_Rohn_Remembering is set to 1 the procedure will store in the array ALIAS_Rohn_Matrix a set of at most ALIAS_Rohn_Remembering_Step matrices for which the Rohn test has already been done, together with at which step the test has failed (the calculation of the determinant of the scalar matrices is always done in the same order). This may allow to avoid a large number of determinant calculation.
Regularity of matrix with linear elements
Mathematical background
Let assume that a parametric matrix has rows (or columns) in which some elements depend linearly on some of the unknowns. Let consider the set- for row
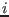 let
let 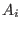 be the elements that depend linearly on
the unknowns
be the elements that depend linearly on
the unknowns
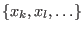 (called the linear unknowns)
(called the linear unknowns)
- construct all possible rows for row
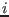 by fixing the linear
unknowns either to their minimum or maximum
by fixing the linear
unknowns either to their minimum or maximum
- construct the set
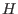 by taking all possible combinations of all
rows
by taking all possible combinations of all
rows
Implementation
A regularity test based on this approach is implemented as:
int ALIAS_Check_Regularity_Linear_Matrix(int DimA,
INTERVAL_VECTOR (* Func)(int l1, int l2,INTERVAL_VECTOR & v_IS),
int (* A_Cond)(int dimA,
INTERVAL_VECTOR (* Func1)(int l1, int l2,INTERVAL_VECTOR &v_IS),
INTERVAL_VECTOR & v_IS,INTERVAL_MATRIX &A),
int Row_Or_Column,
int Context,
INTEGER_MATRIX &Implication_Var,
int Use_Rohn,
INTERVAL_VECTOR &Domain)
where
- Row_Or_Column: 1 if the row of the matrix are used, 2 if the columns are used
- Context: is used to determine if this procedure is used
according to the following rules (see section 7.4 for the
meaning of the flag Simp_in_Cond):
- always used if 100 or if Context is equal to Simp_in_Cond
- not used if Context lie in [-2,2]
- not used if Context=3 and Simp_in_Cond
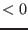
- not used if Context=4 and Simp_in_Cond
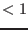
- not used if Context=5 and Simp_in_Cond is not 0 or 1
- not used if Context=6 and Simp_in_Cond is not 0 or 2
- Implication_Var: an integer matrix of dimension DimA
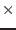
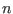 , where
, where 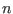 is the number of unknowns. If this matrix has
a 1 at row
is the number of unknowns. If this matrix has
a 1 at row 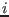 , column
, column 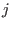 , then the unknown
, then the unknown 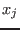 appear linearly in
some elements of row
appear linearly in
some elements of row 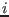 (or column
(or column 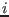 ) of the matrix
) of the matrix 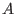
- Use_Rohn: 1 if the Rohn consistency test is used to check
that a matrix in
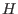 has a constant sign
has a constant sign
- Domain: the ranges for the input parameters
Characteristic polynomial
It is possible to calculate the coefficients of the characteristic polynomial of a real or interval matrix using the procedures:
INTERVAL_VECTOR Poly_Characteristic(INTERVAL_MATRIX &A) INTERVAL_VECTOR Poly_Characteristic(MATRIX &A)
In both cases the coefficients are returned as an interval vector which contains the coefficients of the polynomial by increasing order.
Spectral radius
Safe calculation of the spectral radius of a square real or interval matrix may be obtained with the procedures
int Spectral_Radius(INTERVAL_MATRIX &AA,double eps,double *ro,int iter) int Spectral_Radius(MATRIX &AA,double eps,double *ro,int inter)where
- AA: the matrix
- eps: a real that will be used to increment the solutions found for the median polynomial (i.e. the polynomial whose coefficients are the mid-point of the interval coefficients of the characteristic polynomial) until the polynomial evaluation does not contain 0
- ro: the upper bound of the spectral radius
- iter: the maximal number of allowed iteration
int Spectral_Radius(INTERVAL_MATRIX &AA,double eps,double *ro) int Spectral_Radius(MATRIX &AA,double eps,double *ro)may also be used with a maximum number of iteration fixed to 100.
If it intended just to show that the spectral radius is larger than a given value seuil then you may use
int Spectral_Radius(INTERVAL_MATRIX &A,double eps,double *ro,double seuil); int Spectral_Radius(MATRIX &A,double eps,double *ro,double seuil); int Spectral_Radius(INTERVAL_MATRIX &A,double eps,double *ro,int iter,double seuil); int Spectral_Radius(MATRIX &A,double eps,double *ro,int iter,double seuil);Note that the calculation of the spectral radius may be used to check the regularity of an interval matrix. Indeed let
Let
where