- Introduction
- Finding bounds on the roots
- First Cauchy theorem
- Second Cauchy theorem
- Third Cauchy theorem
- Lagrange-MacLaurin theorem
- Laguerre method
- Laguerre second method
- Newton method
- Newton theorem
- Joyal bounds
- Pellet method
- Global implementation
- Kantorovitch theorem
- Bounds on the product and sum of roots
- Maximum number of real roots
- Number of real roots
- Separation between the roots
- Analyzing the real roots
- Analyzing the real part of the roots
- Utilities
Analyzing univariate polynomials
Introduction
In this chapter we intend to determine some information on the roots of an univariate polynomial without solving it. A polynomial is defined by the list of its coefficient ordered along increasing power in a data structure of type VECTOR. For most of the procedures defined in the sequel the coefficients may also intervals, in which case the data structure is of type INTERVAL_VECTOR (this type of polynomial will be called interval polynomial).
Finding bounds on the roots
First Cauchy theorem
Mathematical background
Let with
Then the modulus of any root
Implementation
This procedure is implemented as:int Cauchy_First_Bound_Interval(int Degree,VECTOR &Coeff,INTERVAL &Bound);with:
- Degree: degree of the polynomial
- Coeff: the Degree+1 coefficients of the polynomial in increasing degree
- Bound: the interval on the absolute value of the roots
int Cauchy_First_Bound_Interval(int Degree,INTERVAL_VECTOR &Coeff,INTERVAL &Bound);This procedure returns an interval
Example
LetCoeff(1)= -3;Coeff(2)=2;Coeff(3)=-1;Coeff(4)=1; Num=Cauchy_First_Bound_Interval(3,Coeff,Bound); Coeff_App(1)= INTERVAL(-3.1,-2.9);Coeff_App(2)=INTERVAL(1.9,2.1); Coeff_App(3)=INTERVAL(-1.1,-0.9);Coeff_App(4)=INTERVAL(0.9,1.1); Num=Cauchy_First_Bound_Interval(3,Coeff_App,Bound);In the first case the procedure find that the absolute value of the roots lie in [0.6,4] while in the second case the range is [0.58,4.44444].
Second Cauchy theorem
Mathematical background
Let with
Note that if
Implementation
This procedure is implemented as:int Cauchy_Second_Bound_Interval(int Degree,VECTOR &Coeff,double *Bound);with:
- Degree: degree of the polynomial
- Coeff: the Degree+1 coefficients of the polynomial in increasing degree
- bound: the upper bound of the positive roots
int Cauchy_Second_Bound_Inverse_Interval(int Degree,VECTOR &Coeff,double *Bound);This procedure fail and returns 0 if Degree=0, Degree=1 and Coeff(2)=0 or Coeff(1)=0. There is also an implementation for interval polynomial:
int Cauchy_Second_Bound_Interval(int Degree,INTERVAL_VECTOR &Coeff,INTERVAL Bound);This procedure will return a failure code of 0 if Degree=0, Degree=1 and Coeff(2) contain 0, or if Coeff(Degree+1) contains 0. In that case if Bound=[a,b], then for all polynomials in the set the positive roots are all lower than b while for some polynomial in the set the roots are lower than a. Equivalently we have:
int Cauchy_Second_Bound_Inverse_Interval(int Degree,INTERVAL_VECTOR &Coeff,INTERVAL Bound);In that case if Bound=[a,b], then for all polynomials in the set the positive roots are all lower than a while for some polynomial in the set the roots are lower than b.
A global procedure enable to get at the same time the upper and lower bound of the positive roots:
int Cauchy_Second_Bound_Interval(int Degree,VECTOR &Coeff,INTERVAL &Bound);
int Cauchy_Second_Bound_Interval(int Degree,INTERVAL_VECTOR &Coeff,
INTERVAL &Lower,INTERVAL &Upper);
In the latter case the interval lower bound is in Lower and the
interval upper bound in Upper.
It is also possible to determine the lower bound of the negative roots using
the procedures:
int Cauchy_Second_Bound_Negative_Interval(int Degree,VECTOR &Coeff,double *Bound); int Cauchy_Second_Bound_Negative_Interval(int Degree,INTERVAL_VECTOR &Coeff,INTERVAL &Bound);while the upper bound of the negative roots can be determined using:
int Cauchy_Second_Bound_Negative_Inverse_Interval(int Degree,VECTOR &Coeff,double *Bound);
int Cauchy_Second_Bound_Negative_Inverse_Interval(int
Degree,INTERVAL_VECTOR &Coeff,
INTERVAL &Bound);
Both the upper and lower bound of the negative roots can be found
using:
int Cauchy_Second_Bound_Negative_Interval(int Degree,VECTOR &Coeff,INTERVAL &Bound);
int Cauchy_Second_Bound_Negative_Interval(int Degree,INTERVAL_VECTOR &Coeff,
INTERVAL &Lower,INTERVAL &Upper);
Example
LetCoeff(1)= -3;Coeff(2)=2;Coeff(3)=-1;Coeff(4)=1; Num=Cauchy_Second_Bound_Interval(3,Coeff,&bound); Coeff_App(1)= INTERVAL(-3.1,-2.9);Coeff_App(2)=INTERVAL(1.9,2.1); Coeff_App(3)=INTERVAL(-1.1,-0.9);Coeff_App(4)=INTERVAL(0.9,1.1); Num=Cauchy_Second_Bound_Interval(3,Coeff_App,Bound);In the first case we find that all the roots are lower than 2 and in the second that the roots have bounds [2.44444,2.44444]. If we have used the lower bound procedures we will have found that all the roots are positive.
Third Cauchy theorem
Mathematical background
This procedure calculates a bound for the absolute value of the roots
of the polynomial, see Handbook of numerical analysis, Ciarlet, Lions,
Volume 3.
Implementation
int Cauchy_Third_Bound_Interval(int Degree,INTERVAL_VECTOR &Coeff,INTERVAL &Bound)Coeff[1] cannot be 0. The procedure:
int Cauchy_All_Bound_Interval(int Degree,INTERVAL_VECTOR &Coeff,
INTERVAL &Bound)
will return the result of a successive application of the first and
third Cauchy bounds.
Lagrange-MacLaurin theorem
Mathematical background
LetAssume
The upper bound ![]() of the value of the positive real root is:
of the value of the positive real root is:
where
If we define:
Then the upper bound of the positive real roots of
![\begin{displaymath}
m=\frac{1}{1+\sqrt[n-k]{\frac{B}{a_n}}}
\end{displaymath}](img516.png)
Implementation
This procedures is implemented as:int MacLaurin_Bound_Interval(int Degree,VECTOR &Coeff,double *Bound);with:
- Degree: degree of the polynomial
- Coeff: the Degree+1 coefficients of the polynomial in increasing degree
- bound: the upper bound of the positive roots
On success the return code is 1. There is also a procedure for the interval polynomial:
int MacLaurin_Bound_Interval(int Degree,INTERVAL_VECTOR &Coeff,INTERVAL Bound);This procedure fail and returns 0 if Degree=0, Degree=1 and
It is also possible to determine the lower bound of the positive roots using the procedures:
int MacLaurin_Bound_Inverse_Interval(int Degree,VECTOR &Coeff,double *Bound); int MacLaurin_Bound_Inverse_Interval(int Degree,INTERVAL_VECTOR &Coeff,INTERVAL &Bound);In the later case if Bound=[a,b], then for all polynomials in the set the roots are all lower than a while for some polynomial in the set the roots are lower than b. To get directly both lower and upper bound of the positive roots you may use:
int MacLaurin_Bound_Interval(int Degree,VECTOR &Coeff,INTERVAL &Bound) int MacLaurin_Bound_Interval(int Degree,INTERVAL_VECTOR &Coeff,INTERVAL &Lower, INTERVAL &Upper)In the latter case the interval lower bound is in Lower and the interval upper bound in Upper.
It is also possible to determine the lower bound of the negative roots using the procedures:
int MacLaurin_Bound_Negative_Interval(int Degree,VECTOR &Coeff,double *Bound); int MacLaurin_Bound_Negative_Interval(int Degree,INTERVAL_VECTOR &Coeff,INTERVAL &Bound);Similarly it is possible to determine the upper bound of the negative roots using the procedures:
int MacLaurin_Bound_Negative_Inverse_Interval(int Degree,VECTOR &Coeff,double *Bound);
int MacLaurin_Bound_Negative_Inverse_Interval(int Degree,
INTERVAL_VECTOR &Coeff,INTERVAL &Bound);
To get directly both lower and upper bound of the negative roots you may use:
int MacLaurin_Bound_Negative_Interval(int Degree,VECTOR &Coeff,INTERVAL &Bound)
int MacLaurin_Bound_Negative_Interval(int Degree,INTERVAL_VECTOR &Coeff,
INTERVAL &Lower, INTERVAL &Upper)
Example
LetCoeff(1)= -3;Coeff(2)=2;Coeff(3)=-1;Coeff(4)=1; Num=MacLaurin_Bound_Interval(3,Coeff,&bound); Coeff_App(1)= INTERVAL(-3.1,-2.9);Coeff_App(2)=INTERVAL(1.9,2.1); Coeff_App(3)=INTERVAL(-1.1,-0.9);Coeff_App(4)=INTERVAL(0.9,1.1); Num=MacLaurin_Bound_Interval(3,Coeff_App,Bound);In the first case we find that all the roots are lower than 4 and in the second that the roots have bounds [4.44444,4.44444]. If we have used the lower bound procedures we will have found that all the roots are greater than -1.
Laguerre method
Mathematical background
Letwith
If it exists a real
- let
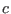 be such that
be such that 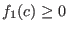
- let
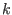 the smallest integer such that either
the smallest integer such that either 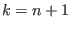 or
or 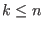 and
and 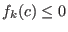
- if
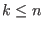 then substitute
then substitute 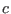 by
by 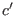 such that
such that
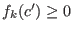 and go to 2
and go to 2
- return
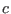
Implementation
This procedure is able to give upper and lower bound on the value of the roots. In the implementation we defineint Laguerre_Bound_Interval(int Degree,VECTOR &Coeff,double sens,int MaxIter,double *bound);with:
- Degree: degree of the polynomial
- Coeff: the Degree+1 coefficients of the polynomial in increasing degree
- sens: a positive real indicating the increase of
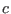 in the
scheme
in the
scheme
- MaxIter: the maximum number of iteration. If this number is exceeded the procedure returns 0.
- bound: the upper value of the real root
The lower bound of the root may be determined by:
int Laguerre_Bound_Inverse_Interval(int Degree,VECTOR &Coeff1,double amp_sens,
int MaxIter,double *bound);
We have also a procedure which determine upper and lower bound for the
real roots:
int Laguerre_Bound_Interval(int Degree,VECTOR &Coeff,double sens,int MaxIter,INTERVAL &Bound);All the real roots lie within Bound. We may also use this procedure for interval polynomial:
int Laguerre_Bound_Interval(int Degree,INTERVAL_VECTOR &Coeff,double sens,
int MaxIter,INTERVAL &Bound);
This procedure fail and returns 0 if Degree=0,
int Laguerre_Bound_Interval(int Degree,INTERVAL_VECTOR &Coeff,double sens,
int MaxIter,INTERVAL &Lower,INTERVAL &Upper);
In that case Upper=[a,b] will be such that
value of all roots of any
polynomial within the set is lower than b, while for some polynomial
they will be lower than a. On the other hand Lower=[a,b]
will be such that the
value of all roots of any
polynomial within the set is greater than a, while for some polynomial
they will be greater than b.
Example
The procedure:Coeff(1)= -3;Coeff(2)=2;Coeff(3)=-1;Coeff(4)=1; Num=Laguerre_Bound_Interval(3,Coeff,0.1,50,Bound); Coeff_App(1)= INTERVAL(-3.1,-2.9);Coeff_App(2)=INTERVAL(1.9,2.1); Coeff_App(3)=INTERVAL(-1.1,-0.9);Coeff_App(4)=INTERVAL(0.9,1.1); Num=Laguerre_Bound_Interval(3,Coeff_App,0.1,50,Lower,Upper);leads to Bound=[1.15385,1.3], Lower=[1.08209,1.40271], Upper=[1.21818,1.52222].
Laguerre second method
Mathematical background
LetAssume that
Implementation
This procedure enable to determine upper and lower bound on the roots of a polynomial if all the roots are real. In the implementation we check if all the roots of the polynomial are real using Huat theorem (see section 5.5.4) and if the answer is positive we determine the bounds. The syntax is:int Laguerre_Second_Bound_Interval(int Degree,VECTOR &Coeff,INTERVAL &Bound);with:
- Degree: degree of the polynomial
- Coeff: the Degree+1 coefficients of the polynomial in increasing degree
- Bound: upper and lower bound on the roots
int Laguerre_Second_Bound_Interval(int Degree,
INTERVAL_VECTOR &Coeff,INTERVAL &Lower,INTERVAL &Upper);
In that case Upper=[a,b] will be such that the maximal
value of all roots of any
polynomial within the set is lower than b, while for some polynomial
they will be lower than a. On the other hand Lower=[a,b]
will be such that the minimal
value of all roots of any
polynomial within the set is greater than a, while for some polynomial
they will be greater than b.
Newton method
Mathematical background
Letwith
- let
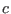 be such that
be such that
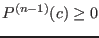
- let
 the smallest integer such that either
the smallest integer such that either 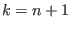 or
or 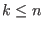 and
and
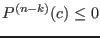
- if
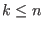 then substitute
then substitute 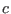 by
by 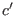 such that
such that
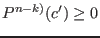 and go to 2
and go to 2
- return
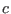
Implementation
This procedure is able to give upper and lower bound on the value of the roots.
In the implementation we define ![]() as the smallest real which satisfy
as the smallest real which satisfy
![]() . If we find
. If we find ![]() such that
such that
![]() , then we
increase
, then we
increase ![]() by a given positive value sens and start again. We
limit the number of iteration of the scheme by giving a maximal value
for the number of iteration:
by a given positive value sens and start again. We
limit the number of iteration of the scheme by giving a maximal value
for the number of iteration:
int Newton_Bound_Interval(int Degree,VECTOR &Coeff1,double amp_sens,int MaxIter,double *bound);with:
- Degree: degree of the polynomial
- Coeff: the Degree+1 coefficients of the polynomial in increasing degree
- sens: a positive real indicating the increase of
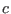 in the
scheme
in the
scheme
- MaxIter: the maximum number of iteration. If this number is exceeded the procedure returns 0.
- bound: the upper value of the real root
int Newton_Bound_Inverse_Interval(int Degree,VECTOR &Coeff1,double amp_sens,
int MaxIter,double *bound);
We have also a procedure which determine upper and lower bound for the
real roots:
int Newton_Bound_Interval(int Degree,VECTOR &Coeff1,double amp_sens,
int MaxIter,INTERVAL &Bound);
All the real roots lie within Bound. We may also use this
procedure for interval polynomial:
int Newton_Bound_Interval(int Degree,INTERVAL_VECTOR &Coeff,double sens,
int MaxIter,INTERVAL &Bound);
This procedure fail and returns 0 if Degree=0,
int Newton_Bound_Interval(int Degree,INTERVAL_VECTOR &Coeff,double sens,
int MaxIter,INTERVAL &Lower,INTERVAL &Upper);
In that case Upper=[a,b] will be such that
value of all roots of any
polynomial within the set is lower than b, while for some polynomial
they will be lower than a. On the other hand Lower=[a,b]
will be such that the
value of all roots of any
polynomial within the set is greater than a, while for some polynomial
they will be greater than b.
Newton theorem
Mathematical background
Letwith
Implementation
This procedure is able to give an upper bound on the absolute value of the roots as soon as all the roots are real (this is checked using Huat theorem, section 5.5.4). The syntax is:int Newton_Second_Bound_Interval(int Degree,VECTOR &Coeff,double *bound);with:
- Degree: degree of the polynomial
- Coeff: the Degree+1 coefficients of the polynomial in increasing degree
- bound: upper bound on the absolute value of the roots
int Newton_Second_Bound_Inverse_Interval(int Degree,VECTOR &Coeff,double *bound);An upper and lower bound on the absolute value of the roots may be compute by:
int Newton_Second_Bound_Interval(int Degree,VECTOR &Coeff,INTERVAL &Bound);In that case if Bound=[a,b] we have for all root
Similar procedures exist for interval polynomial:
int Newton_Second_Bound_Interval(int Degree,INTERVAL_VECTOR &Coeff,INTERVAL &Bound); int Newton_Second_Bound_Inverse_Interval(int Degree,INTERVAL_VECTOR &Coeff,INTERVAL &Bound); int Newton_Second_Bound_Interval(int Degree,INTERVAL_VECTOR &Coeff,INTERVAL &L, INTERVAL &U);where
- Bound: upper or lower bound on the absolute value of the root of the polynomials
- L,U: if L=[a,b] then the absolute value of the roots of any polynomial in the set is greater than a while some polynomial have root greater than b. Conversely if U=[a,b] the absolute value of the roots of any polynomial in the set is lower than b while some polynomial have root lower than a.
Joyal bounds
Mathematical background
Let a polynomial whose interval coefficients have a fixed sign. Let
Implementation
int Joyal_Bound_Interval(int Degre,INTERVAL_VECTOR &Coeff,INTERVAL &Bound)returns in Bound an upper bound of the modulus of the roots of the polynomial of degree Degre and interval coefficients Coeff. The procedure returns 0 if
Pellet method
Mathematical background
Let
Now assume that we have calculated the coefficients of the polynomial
![]() where
where ![]() are known quantities. If we determine a
are known quantities. If we determine a ![]() polynomial that has 2 positive roots
polynomial that has 2 positive roots ![]() in the range
in the range ![]() ,
then
,
then ![]() has roots in the disk
has roots in the disk ![]() . Hence the absolute value of the
real part of the roots is bounded by
. Hence the absolute value of the
real part of the roots is bounded by ![]() . As
. As ![]() we get that
the real part
we get that
the real part ![]() of the root satisfies
of the root satisfies
![]() . As
. As ![]() this shows that
this shows that ![]() has roots whose real part
is greater than
has roots whose real part
is greater than ![]() .
.
Implementation
int Pellet(int Degre,INTERVAL_VECTOR &Coeff,double R)where Degre is the degree of the polynomial, Coeff are the coefficients of the polynomial
Global implementation
The above algorithms have been regrouped in two procedures, one for determining the bound on the positive roots, the other for the negative roots:int Global_Positive_Bound_Interval(int Degree,VECTOR &Coeff,INTERVAL &Bound); int Global_Negative_Bound_Interval(int Degree,VECTOR &Coeff,INTERVAL &Bound);with:
- Degree: degree of the polynomial
- Coeff: the Degree+1 coefficients of the polynomial in increasing degree
- Bound: the bound on the positive or negative roots
- if a bound
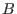 have been previously determined, then the step
size is fixed to
have been previously determined, then the step
size is fixed to 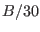 except if the global variable
Step_Laguerre_Interval has been defined to be a double not
equal to 0, in which case this variable is used as the step size.
except if the global variable
Step_Laguerre_Interval has been defined to be a double not
equal to 0, in which case this variable is used as the step size.
- if a bound as not been determined the step size is fixed to 1
except if the global variable
Step_Laguerre_Interval has been defined to be a double not equal to 0, in which case this variable is used as the step size. - if the step if lower than the global variable Min_Step_Laguerre_Interval (which is 0.1 by default) the step is substituted by Min_Step_Laguerre_Interval
int Global_Positive_Bound_Interval(int Degree,INTERVAL_VECTOR &Coeff,
INTERVAL &Lower,INTERVAL &Upper);
int Global_Negative_Bound_Interval(int Degree,INTERVAL_VECTOR &Coeff,
INTERVAL &Lower,INTERVAL &Upper);
where Lower is an interval on the lower bound: for positive
roots and if Lower=[a,b] then the roots of any polynomial in the
set is greater than a while some polynomial have root greater than
b. Conversely if Upper=[a,b] the roots of any polynomial in the
set is lower than b while some polynomial have root lower than a.
Both procedures for real roots have been regrouped in
void ALIAS_Find_Bound_Polynom(int Degree,
INTERVAL_VECTOR (* TheCoeff)(INTERVAL_VECTOR &),
INTERVAL_VECTOR &PALL,INTERVAL &Space, INTERVAL &Bound)
where
- PALL: the first component is the bound for the real roots the polynomial while the following are the value of the parameters for which the bounds will be obtained
- Space: a default bound for the real roots; may be used to indicate that we are looking only for bounds on the positive or negative real roots by specifying a positive or a negative lower bound
- Bound: bounds for the real roots
Example
An interesting example is given by:Coeff_App(1)= INTERVAL(-3.1,-2.9);Coeff_App(2)=INTERVAL(1.9,2.1); Coeff_App(3)=INTERVAL(-1.1,-0.9);Coeff_App(4)=INTERVAL(0.9,1.1); Num=Global_Positive_Bound_Interval(3,Coeff_App,Lower,Upper);which leads to Lower=[1.1487,1.42957], Upper=[1.15224,1.43049].
The above procedure may give some sharp bounds. For example consider
the Wilkinson polynomial of order 22 (which has as roots
1,2,![]() ,21,22) we get 0 negative roots while the positive roots
are bounded by [0.790447,22.1087].
,21,22) we get 0 negative roots while the positive roots
are bounded by [0.790447,22.1087].
The test program Test_Bound_UP enable to test the bound procedures for any polynomial. This program take as first argument the name of a file giving the coefficients of the polynomial by increasing power of the variable. The program will print the bounds determined by all the previous procedures and then the bounds determined using the global implementation. Then the same treatment will be applied on the interval polynomial whose coefficients are intervals centered at the coefficients find in the file with a width of 0.2
Kantorovitch theorem
The mathematical background of Kantorovitch has been explained in
section 3.1.2. This method may determine an interval on the
unknown in which there is an unique solution, toward which Newton
method will converge (see section 2.9).
Implementation
The syntax of the algorithm is:int Kantorovitch(int Degree,VECTOR &Coeff,REAL Input,double *eps)with
- Degree: degree of the polynomial
- Coeff: coefficients of the polynomial ordered along increasing degree
- Input: center of the interval in which an unique solution occur
- eps: half width of the solution interval
int Kantorovitch(int Degree,INTERVAL_VECTOR &Coeff,REAL Input,double *eps)If this procedure returns 1, then any polynomial in the set of interval polynomial has an unique solution in the interval [Input-eps,Input+eps]. There is also an implementation which take into account rounding errors:
int Kantorovitch_Fast_Safe(int Degree,INTERVAL_VECTOR &Coeff,REAL Input,double *eps)in which "safe" interval value of the coefficients have been pre-computed.
Example
LetCoeff(1)= -3;Coeff(2)=2;Coeff(3)=-1;Coeff(4)=1; Num=Kantorovitch(3,Coeff,1.2,&eps); Coeff_App(1)= INTERVAL(-3.1,-2.9);Coeff_App(2)=INTERVAL(1.9,2.1); Coeff_App(3)=INTERVAL(-1.1,-0.9);Coeff_App(4)=INTERVAL(0.9,1.1); Num=Kantorovitch(3,Coeff_App,1.2,&eps);In the first case Kantorovitch returns 1 and has determined that there is an unique solution in the interval [1.04082,1.35918]. Using Newton method we find the root 1.27568220371567 with residue 2.80147904874184e-10. For the interval polynomial Kantorovitch returns also 1 and find an unique solution in [1.05718,1.34282].
Bounds on the product and sum of roots
Newton relations
Mathematical background
Letand
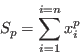
We have [4]:
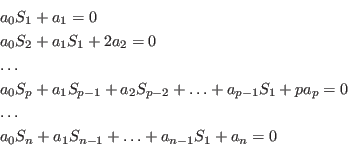
Implementation
Let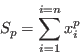
This procedure enable to compute the
VECTOR SumN_Polynomial_Interval(int Degree,VECTOR &Coeff)with:
- Degree: degree of the polynomial
- Coeff: coefficients of the polynomial ordered along increasing degree
INTERVAL_VECTOR SumN_Polynomial_Interval(int Degree,INTERVAL_VECTOR &Coeff)which returns intervals including the
Viète relations
Mathematical background
Letand
We have [4]:
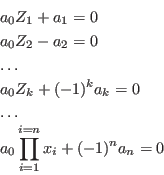
Implementation
LetThis procedure enable to compute the
VECTOR ProdN_Polynomial_Interval(int Degree,VECTOR &Coeff)with:
- Degree: degree of the polynomial
- Coeff: coefficients of the polynomial ordered along increasing degree
INTERVAL_VECTOR ProdN_Polynomial_Interval(int Degree,INTERVAL_VECTOR &Coeff)which returns intervals including the
Maximum number of real roots
Number of real roots
Descartes Lemma
Mathematical background
Letwith
Implementation
The syntax of the procedure is:INT Descartes_Lemma_Interval(int Degree,VECTOR &Coeff)with:
- Degree: degree of the polynomial
- Coeff: the Degree+1 coefficients of the polynomial in increasing degree
There is an implementation of this method for interval polynomial. Here it is necessary to introduce an additional parameter to indicate the confidence we have in the result. The procedure is implemented as:
INT Descartes_Lemma_Interval(int Degree,INTERVAL_VECTOR &Coeff,int *Confidence);Confidence is a quality index:
- 1: the result is exact, for all polynomials in the set the
number of positive real roots is
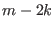
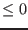 : the number of positive real roots for all the
polynomials
in the set is
: the number of positive real roots for all the
polynomials
in the set is 
INT Descartes_Lemma_Negative_Interval(int Degree,VECTOR &Coeff) INT Descartes_Lemma_Negative_Interval(int Degree,INTERVAL_VECTOR &Coeff,int *Confidence)
Budan-Fourier method
Mathematical background
Budan-Fourier algorithm is a simple method which enable to determine easily some information on the number of root of a given univariate polynomial within a given interval. Letand
Implementation
This procedure is used to determine the number of real roots in a given interval, up to an even number. The syntax of the procedure is:INT Budan_Fourier_Interval(int Degree,VECTOR &Coeff,INTERVAL In) INT Budan_Fourier_Interval(int Degree,INTEGER_VECTOR &Coeff,INTERVAL In)with:
- Degree: degree of the polynomial
- Coeff: the Degree+1 coefficients of the polynomial in increasing degree, which may be REAL or INT
- In: the interval in which we are looking for the number of roots
- -1:
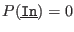
- -2:
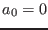 , the polynomial may be factored
, the polynomial may be factored
- -3:
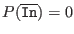
INT Budan_Fourier_Interval(int Degree,INTERVAL_VECTOR &Coeff,INTERVAL In,int *Confidence)where Confidence is a quality index for the result:
- 1: the result is exact, so if
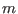 is the return code of the
algorithm the number of reals roots of the interval polynomial is
is the return code of the
algorithm the number of reals roots of the interval polynomial is
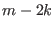 with
with ![$k\in[0,m/2]$](img585.png)
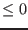 : if
: if 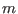 is the return code of the
algorithm the number of reals roots of the interval polynomial is
is the return code of the
algorithm the number of reals roots of the interval polynomial is 
INT Budan_Fourier_Safe_Interval(int Degree,VECTOR &Coeff,
INTERVAL In,INTERVAL &NbRoot);
The procedure returns 1 in case of success and an interval for the
number of roots. If NbRoot=[a,b], then if a =b the number of
roots is either a,a-2,
INT Budan_Fourier_Fast_Safe_Interval(int Degree,INTERVAL_VECTOR &Coeff,
INTERVAL In,INTERVAL &NbRoot);
Another safe procedure is:
INT Budan_Fourier_Interval(int Degree,INTEGER_VECTOR &Coeff,int Inf,int Sup)where the coefficients and the bounds are integers.
Example
LetCoeff(1)= -3;Coeff(2)=2;Coeff(3)=-1;Coeff(4)=1; P=INTERVAL(0.0,2.0); Num= Budan_Fourier_Interval(3,Coeff,P);Num is 3 meaning that
Coeff_App(1)= INTERVAL(-3.1,-2.9); Coeff_App(2)=INTERVAL(1.9,2.1); Coeff_App(3)=INTERVAL(-1.1,-0.9); Coeff_App(4)=INTERVAL(0.9,1.1); Num= Budan_Fourier_Interval(Degree,Coeff_App,P,&Confidence);Num is also 3 with Confidence=1 meaning that the number of roots for any polynomial is either 3 or 1.
Sturm method
Mathematical background
Let a polynomialLet
The drawback of Sturm method is that the absolute value of the coefficients increase quickly when computing the sequence. Numerical rounding errors may then affect the result. The alternate method of Budan-Fourier (see section 5.5.2) is less sensitive to rounding errors although it provides less information than Sturm method.
Implementation
This procedure determines the number of real roots of an univariate polynomial in a given interval. It is implemented as:
int Sturm_Interval(int Degree,VECTOR &Coeff,INTERVAL &In); int Sturm_Interval(int Degree,INTEGER_VECTOR &Coeff,INTERVAL &In);
- Degree: degree of the polynomial
- Coeff: the Degree+1 coefficients of the polynomial in increasing degree, either real or integers
- In: the interval in which we are looking for the number of roots
int Sturm_Safe_Interval(int Degree,VECTOR &Coeff,INTERVAL &In,INTERVAL &NbRoot);which returns 1 in case of success and an interval NbRoot which contain the number of roots. If NbRoot=[a,b], then if a =b the number of roots is a and if a
int Sturm_Interval(int Degree,INTEGER_VECTOR &Coeff,int Inf,int Sup);This procedure will return -1 if all the coefficients are 0 and -2 if at some point of the process an integer larger than the largest machine integer is encountered (Not yet implemented).
Example
We use as example the Wilkinson polynomial of degree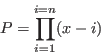
and we are looking for roots in the interval [0.5,0.7] the procedure Sturm_Interval returns always 0 for order 4 to 20. But starting at order 9 the safe procedure returns [0,3] while the safe Budan-Fourier procedure still returns 0.
The test program Test_Nb_Root_Up enable to test Budan-Fourier and Sturm method on any polynomial whose coefficients are defined in a file, by increasing degree of the power of the unknown.
Du Gua-Huat-Euler theorem
Mathematical background
LetIf all the roots of
Conversely if this relation does not hold for some
Implementation
This procedure enable to determine if the roots of a polynomial are all real. It is implemented in a safe way i.e. if they are numerical errors in the coefficients and if the procedure determine that all the roots are real the result is guaranteed. The syntax is:int Huat_Polynomial_Interval(int Degree,VECTOR &Coeff);with:
- Degree: degree of the polynomial
- Coeff: the Degree+1 coefficients of the polynomial in increasing degree
int Huat_Polynomial_Interval(int Degree,INTERVAL_VECTOR &Coeff);This procedure will return 1 if all the polynomials in the set have their roots real, -1 if some polynomials in the set have all roots real but some others have complex roots and 0 if all the polynomials in the set have complex roots.
Separation between the roots
Rump theorem
Mathematical background
Letand let
The minimal distance
Implementation
The procedure is able to determine a lower bound on the distance between two real roots of a polynomial:int Min_Sep_Root_Interval(int Degree,VECTOR &Coeff,double &min);with
- Degree: degree of the polynomial
- Coeff: the Degree+1 coefficients of the polynomial in increasing degree
- min: the lower bound on the distance between two real roots
int Max_Sep_Root_Interval(int Degree,VECTOR &Coeff,double &max);while upper and lower bounds may be determined with:
int Bound_Sep_Root_Interval(int Degree,VECTOR &Coeff,INTERVAL &Bound);There is also a procedure to determine a lower bound for interval polynomial:
int Min_Sep_Root_Interval(int Degree,INTERVAL_VECTOR &Coeff,INTERVAL &Lower);If Lower=[a,b] then some polynomials in the set will have a minimal distance between the roots greater than b while all the polynomials in the set have a minimal distance greater than a.
Example
Clearly this formula give an underestimated value of the minimal distance between the roots. For example if we consider a Wilkinson polynomial of order 4 (which has therefore 1,2,3,4 as roots) we find that the minimal and maximal distance between the roots are bounded by [7.07107e-09,1.41421e+08].
Analyzing the real roots
int ALIAS_Min_Max_Is_Root(int Degree, int NbParameter, int HasInterval, INTERVAL_VECTOR (* TheCoeff)(INTERVAL_VECTOR &), int Iteration, INTERVAL_VECTOR &Par, double *Root, int Type, int (* Solve_Poly)(double *, int *,double *))may be used to rest if a polynomial in a set may have as real root one of two pre-defined value.
- Degree: the degree of the polynomial
- NbParameter: the number of parameters that appear in the coefficient of the polynomial
- HasInterval: 1 if the coefficient include intervals not defined by parameters, 0 otherwise
- TheCoeff: a procedure to calculate the coefficients of the polynomial being given range for the parameters
- Iteration: the maximum number of box that may be used by the algorithm
- Par: the ranges for the parameters
- Root: we look for polynomial whose real part of the root is either Root[0] or Root[1]
- Type:
- -1 : if in a box we have found a polynomial with a root lower than Root[0]; we look for a polynomial in the box whose real root is exactly Root[0]. If no such polynomial is found the box is eliminated
- 1 : if in a box we have found a polynomial with a root greater than Root[1]; we look for a polynomial in the box whose real root is exactly Root[1]. If no such polynomial is found the box
- 2: if in a box we have found a polynomial with a root greater than Root[1] and a polynomial with a real root greater than Root[0]; we look for a polynomial in the box whose real root is exactly Root[1] and a polynomial whose real root is exactly Root[0]. If no such polynomials are found the box is eliminated
- 0: general case;
- Solve_Poly: a procedure to solve polynomial with double floating point coefficients. The first argument are the coefficients, the second the degree of the polynomial and the third the real roots
Analyzing the real part of the roots
For some applications it may be interesting to determine if a polynomial in a set defined by a parametric polynomial has the real part of one of its roots equal to a pre-defined value. This may be done by using the procedure
int ALIAS_Is_Root_RealPart(int Degree,
int NbParameter,
int HasInterval,
INTERVAL_VECTOR (* TheCoeff)(INTERVAL_VECTOR &),
INTERVAL_VECTOR (* TheCoeffCentered)(INTERVAL_VECTOR&,double a),
int Iteration,
INTERVAL_VECTOR &Par,
double *Root,
INTERVAL_VECTOR (* EvaluateComplex)(int,int,INTERVAL_VECTOR &),
int (* Simp)(INTERVAL_VECTOR &))
where
- Degree: the degree of the polynomial
- NbParameter: the number of parameters that appear in the coefficient of the polynomial
- HasInterval: 1 if the coefficient include intervals not defined by parameters, 0 otherwise
- TheCoeff: a procedure to calculate the coefficients of the polynomial being given range for the parameters
- TheCoeffCentered: a procedure to calculate the
coefficients of the polynomial
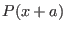
- Iteration: the maximum number of box that may be used by the algorithm
- Par: the ranges for the parameters
- Root: we look for polynomial whose real part of the root is either Root[0] or Root[1]
- EvaluateComplex: a procedure that returns 4 intervals. The
input interval vector has dimension NbParameter+1 elements, the
first one being the parameters, the last one being
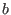 . The procedure
should evaluate
. The procedure
should evaluate
![$U=P(Root[0]+I b), V=P(Root[1]+I b)$](img620.png) and should
return the real part of
and should
return the real part of 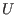 , the complex part of
, the complex part of 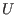 ,
the real part of
,
the real part of 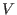 and the complex part of
and the complex part of 
- Simp: an optional simplification procedure that returns -1 if the polynomials in a set cannot roots with real part equal to Root[0] or Root[1]
Utilities
Addition of two polynomials
The following procedures enable to add polynomials with real,interval or integer coefficients:
VECTOR Add_Polynomial_Interval(int n1,VECTOR &Coeff1,int n2,VECTOR &Coeff2);
INTERVAL_VECTOR Add_Polynomial_Interval(int n1,INTERVAL_VECTOR &Coeff1,
int n2,INTERVAL_VECTOR &Coeff2);
INTEGER_VECTOR Add_Polynomial_Interval(int n1,INTEGER_VECTOR &Coeff1,
int n2,INTEGER_VECTOR &Coeff2);
with:
- ni: degree of the polynomial
- Coeffi: the coefficients of the polynomials in increasing degree
INTERVAL_VECTOR Add_Polynomial_Safe_Interval(int n1,VECTOR &Coeff1,int n2,VECTOR &Coeff2);
Multiplication of two polynomials
The following procedures returns the degree of the product of two polynomial either with real or integer coefficients:
int Degree_Product_Polynomial_Interval(int n1,VECTOR &Coeff1,int n2,VECTOR &Coeff2);
int Degree_Product_Polynomial_Interval(int n1,INTEGER_VECTOR &Coeff1,int n2,
INTEGER_VECTOR &Coeff2);
Then you may use the following procedure to compute the product of
polynomial either with real,integer or interval coefficients:
VECTOR Multiply_Polynomial_Interval(int n1,VECTOR &Coeff1,int n2,VECTOR &Coeff2);
INTEGER_VECTOR Multiply_Polynomial_Interval(int n1,INTEGER_VECTOR &Coeff1,
int n2,INTEGER_VECTOR &Coeff2);
INTERVAL_VECTOR Multiply_Polynomial_Interval(int n1,INTERVAL_VECTOR &Coeff1,
int n2,INTERVAL_VECTOR &Coeff2);
All these procedures return the coefficients of the product, the
leading term being 0 only if one polynomial is equal to 0.
To take into account the rounding errors you may use:
INTERVAL_VECTOR Multiply_Polynomial_Safe_Interval(int n1,VECTOR &Coeff1,int n2,VECTOR &Coeff2);
Evaluation of a polynomial
The evaluation of a polynomial for a given value is implemented as:
REAL Evaluate_Polynomial_Interval(int Degree,VECTOR &Coeff,REAL P) INTERVAL Evaluate_Polynomial_Interval(int Degree,INTERVAL_VECTOR &Coeff,REAL P) INTERVAL Evaluate_Polynomial_Interval(int Degree,VECTOR &Coeff,INTERVAL P) INTERVAL Evaluate_Polynomial_Interval(int Degree,INTERVAL_VECTOR &Coeff,INTERVAL P) REAL Evaluate_Polynomial_Interval(int Degree,INTEGER_VECTOR &Coeff,REAL P); int Evaluate_Polynomial_Interval(int Degree,INTEGER_VECTOR &Coeff,INT P);with:
- Degree: degree of the polynomial
- Coeff: the Degree+1 coefficients (which can be REAL, INT or INTERVAL of the polynomial in increasing degree
- P: the point at which we want to compute the polynomial. It may be REAL, INT or INTERVAL.
- the value of a polynomial with REAL coefficients at a point
- the interval value of a polynomial with interval coefficients at a real point
- the interval value of a polynomial with REAL coefficients at for an interval value of the unknown. The first and second order derivative of the polynomial are used to get sharp bounds
- the interval value of a polynomial with interval coefficients for an interval value of the unknown. The first and second order derivative of the polynomial are used to get sharp bounds
Evaluation in centered form
The previous procedures may yield sometime to a bad evaluation of the
polynomial. For example for the Wilkinson polynomial at order 15 the
evaluation for 15.1 leads to 11977410100.791748046875, the correct
value being 11977396665.006561033796551. The evaluation obtained when
considering that the coefficients and the unknown are intervals is
evidently correct and leads to the interval:
[11977379510.705810546875,11977410100.791748046875]A better evaluation may be obtained if we use a centered form of the polynomial. Consider the polynomials:
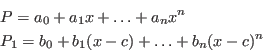
where
VECTOR Coeff_Polynomial_Centered_Interval(int Degree,VECTOR &Coeff,REAL P);
INTERVAL_VECTOR Coeff_Polynomial_Centered_Interval(int Degree,
INTERVAL_VECTOR &Coeff,REAL P);
enable to compute the
INTERVAL_VECTOR Coeff_Polynomial_Centered_Safe_Interval(int Degree,VECTOR &Coeff,REAL P);
INTERVAL_VECTOR Coeff_Polynomial_Centered_Fast_Safe_Interval(int Degree,
INTERVAL_VECTOR &Coeff,REAL P);
which return safe value for the coefficients (in the second form we
assume that you have pre-computed safe value for the coefficients of
the polynomial using the procedure described in
section 5.9.10).
Then we may use the procedures:
REAL Evaluate_Polynomial_Centered_Interval(int Degree,VECTOR &Coeff,REAL Center,REAL P);
INTERVAL Evaluate_Polynomial_Centered_Interval(int Degree,VECTOR &Coeff,INTERVAL P);
INTERVAL Evaluate_Polynomial_Centered_Interval(int Degree,INTERVAL_VECTOR &Coeff,
REAL Center,REAL P);
INTERVAL Evaluate_Polynomial_Centered_Interval(int Degree,INTERVAL_VECTOR &Coeff,INTERVAL P);
These procedures return the evaluation of the polynomial at P using the
centered form at Center or at the middle point of P if is
an interval. For example for the Wilkinson polynomial at order 15 the
evaluation for 15.1 using the centered form at 15 leads to
11977396665.00650787353516 which is largely better than the previous
evaluation.
Safe evaluation of a polynomial
Due to the numerical error in the coefficients and in INTERVAL Evaluate_Polynomial_Safe_Interval(int Degree,VECTOR &Coeff,REAL P); INTERVAL Evaluate_Polynomial_Safe_Interval(int Degree,VECTOR &Coeff,INTERVAL P); INTERVAL Evaluate_Polynomial_Safe_Interval(int Degree,INTERVAL_VECTOR &Coeff,REAL P); INTERVAL Evaluate_Polynomial_Safe_Interval(int Degree,INTERVAL_VECTOR &Coeff,INTERVAL P);
For example for the Wilkinson polynomial at order 15 the
evaluation for 15.1 leads to the interval:
If "safe" intervals have been pre-computed (for example by using the procedure described in section 5.9.10) for the coefficients you may use:
INTERVAL Evaluate_Polynomial_Fast_Safe_Interval(int Degree,INTERVAL_VECTOR &Coeff,REAL P); INTERVAL Evaluate_Polynomial_Fast_Safe_Interval(int Degree,INTERVAL_VECTOR &Coeff,INTERVAL P);which are faster. If you want to use a centered form you may use:
INTERVAL Evaluate_Polynomial_Centered_Safe_Interval(int Degree,VECTOR &Coeff,REAL P);
INTERVAL Evaluate_Polynomial_Centered_Safe_Interval(int Degree,VECTOR &Coeff,INTERVAL P);
INTERVAL Evaluate_Polynomial_Centered_Fast_Safe_Interval(int Degree,
INTERVAL_VECTOR &Coeff,REAL P);
INTERVAL Evaluate_Polynomial_Centered_Fast_Safe_Interval(int Degree,
INTERVAL_VECTOR &Coeff,INTERVAL P);
in which the two last forms assume that you have pre-computed a safe
value of the coefficients of the polynomial.
The evaluation of a polynomial with real coefficients at a complex point may be performed with:
INTERVAL_VECTOR Evaluate_Complex_Poly(int deg,
INTERVAL_VECTOR &Coeff, INTERVAL &XR,INTERVAL &XI)
where XR is the real part of the point and XI its
imaginary part. This procedure returns an interval vector whose first
element is the real part of the evaluation and the second element its
imaginary part.
Sign of a polynomial
This procedure is able to determine if the sign of a polynomial
evaluated at a given point may be affected by numerical errors.
Implementation
int Sign_Polynomial_Interval(int Degree,VECTOR &Coeff,REAL P) int Sign_Polynomial_Interval(int Degree,INTERVAL_VECTOR &Coeff,REAL P) int Sign_Polynomial_Interval(int Degree,INTERVAL_VECTOR &Coeff,REAL P) int Sign_Polynomial_Interval(int Degree,INTERVAL_VECTOR &Coeff,INTERVAL P)with:
- Degree: degree of the polynomial
- Coeff: the Degree+1 coefficients (which can be REAL or INTERVAL of the polynomial in increasing degree
- P: the point or interval at which we want to compute the polynomial
This procedure returns 1 if the polynomial is positive, -1 if it is negative, 0 if it is 0 and 2 if the sign is either affected by numerical errors (if Coeff and P are REAL) or is not constant (if Coeff or P are INTERVAL_VECTOR).
Derivative of a polynomial
The derivatives of a polynomial may be computed using the procedures:
VECTOR Derivative_Polynomial_Interval(int Degree,VECTOR &Coeff) INTEGER_VECTOR Derivative_Polynomial_Interval(int Degree,INTEGER_VECTOR &Coeff); VECTOR Nth_Derivative_Polynomial_Interval(int Degree,VECTOR &Coeff,int n)These procedures enable to get the coefficients of the first and n-th derivative of a polynomial defined by its REAL or INT coefficients.
Due to rounding errors there may be errors in the coefficients provided by the previous procedures. The procedure:
INTERVAL_VECTOR Derivative_Polynomial_Safe_Interval(int Degree,VECTOR &Coeff);will return an INTERVAL_VECTOR (i.e. a set of intervals) which are guaranteed to include the true value of the coefficients of the derivative. A faster procedure may be used if "safe" interval values of the coefficients have been pre-computed:
INTERVAL_VECTOR Derivative_Polynomial_Fast_Safe_Interval(int Degree,INTERVAL_VECTOR &Coeff);
If we deal with polynomial with interval coefficients the following procedures may be used:
INTERVAL_VECTOR Derivative_Polynomial_Interval(int Degree,INTERVAL_VECTOR &Coeff)
INTERVAL_VECTOR Nth_Derivative_Polynomial_Interval(int Degree,
INTERVAL_VECTOR &Coeff,int n)
Euclidian division
The procedure:
void ALIAS_Euclidian_Division(int Degree,INTERVAL_VECTOR &Coeff1,
INTERVAL_VECTOR &Coeff2,INTERVAL &Residu,INTERVAL &a)
computes the division of the polynomial P with interval coefficients
Coeff1 by x-a and returns the polynomial P1 with coefficients
Coeff2 such that P=(x-a)P1+Residu
Another procedure that perform the same process if a is a double is
void Divide_Single(int Degree,INTERVAL_VECTOR &Coeff1,double a,
INTERVAL_VECTOR &Coeff2, INTERVAL &Residu)
For dividing a polynomial and evaluating the polynomial under this form for some interval
INTERVAL Divide_Evaluate_Multiple(int Degree,INTERVAL_VECTOR &Coeff1,
int n,double *a,INTERVAL_VECTOR &X)
where
- n: the number of terms
- a: the value of
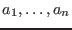
For the Euclidian division by an arbitrary polynomial you may use
int Divide_Polynom(int Degree,INTERVAL_VECTOR &Coeff,int DegreeDivisor,
INTERVAL_VECTOR &CoeffDivisor,
INTERVAL_VECTOR &CoeffQuo, INTERVAL_VECTOR &CoeffRem)
The polynomial Note that Divide_Polynom and Divide_Evaluate_Multiple may be used to perform the deflation of an univariate polynomial as soon as approximate roots for the polynomial have been found. This may be useful to decrease the computation time for solving a polynomial or for numerically instable polynomial such as the Wilkinson polynomial. A combination of Rouche filtering and of deflation allows to solve Wilkinson polynomial of order 18, while the general solving procedure will fail starting at order 13.
A special Euclidian division is the division of a polynomial ![]() by
its derivative. This can be done with
by
its derivative. This can be done with
void Quotient_UP_Derivative(int Degree,VECTOR &Coeff,VECTOR &CoeffD,VECTOR &Quo,
VECTOR &Rem)
where
Expansion of 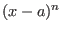
The coefficients of the expansion of the polynomial ![]() may be
obtained with the procedure
may be
obtained with the procedure
INTERVAL_VECTOR Power_Polynomial(INTERVAL &a,int n)which returns the coefficients
Centered form
Let
![]() which may also be written as
which may also be written as
![]() where
where ![]() is some fixed or interval
value. The coefficient
is some fixed or interval
value. The coefficient ![]() may be calculated with the procedure
may be calculated with the procedure
int Derive_Polynomial_Expansion(int n,INTERVAL_VECTOR &Coeff,INTERVAL &a,INTERVAL_VECTOR &B)which returns 1 if the
Unitary polynomial
Let ![]() be a polynomial and be maxroot the maximal modulus of
the root of
be a polynomial and be maxroot the maximal modulus of
the root of ![]() . From
. From ![]() we may derive a polynomial
we may derive a polynomial ![]() such that the
roots of
such that the
roots of ![]() have a modulus lower or equal to 1 and if
have a modulus lower or equal to 1 and if ![]() is a root
of
is a root
of ![]() then maxroot
then maxroot![]() is a root of
is a root of ![]() .
The calculation of the coefficients of
.
The calculation of the coefficients of ![]() may be done with the
procedure
may be done with the
procedure
int Unit_Polynom(int Degree,INTERVAL_VECTOR &Coeff,
double maxroot,INTERVAL_VECTOR &CoeffU)
where Coeff are the coefficients of
Safe evaluation of a vector
Let us consider a VECTOR: due to numerical rounding each element
of this vector represent in fact an interval. The procedure:
INTERVAL_VECTOR Evaluate_Coeff_Safe_Interval(int n,VECTOR &Coeff);with:
- n: size of the vector
- Coeff: the vector