Madalena Chaves
Senior Researcher
(Directrice de Recherche)
Centre Inria d'Université Côte d'Azur
|
|
Madalena Chaves Senior Researcher |
Research
I use different frameworks for modeling dynamical systems: continuous (ordinary differential equations) and discrete systems (Boolean networks), as well as a hybrid formulation combining discrete synthesis terms with linear degradation (piecewise affine systems). A description of some selected topics is given below.
For a quick overview
A theoretical paper, introducing an original idea on how to compute the attractors of a large network through two smaller networks; an exact algorithm which is highly computational cost-saving.
A paper which establishes uniqueness and stability of periodic orbits in a class of n-dimensional systems, forming the basic circuit in circadian clocks, for instance. The paper dedicates two sections to period measurements and model fitting to actual experimental data in plant Arabidopsis thaliana and fruit fly Drosophila melanogaster.
In this work, the cross-fertilization between theoretical work and experimental data is in good evidence: mathematical models were built and refined to improve our understanding of the data produced in J. Roux lab. By using one comprehensive and one compact model view, we were able to identify special reactions or regulatory targets driving heterogeneity.
A paper showing how to combine continuous, hybrid and Boolean networks to obtain a rich, informative and predictive model of a given physical system (here the circadian clock mechanism in cyanobacteria)
Theoretical paper studying the coupling of a network of N similar oscillators and showing that new stable equilibria may appear. This means that the coupled system may potentially deviate from the oscillatory behavior and converge to a steady state, which generates a point of caution when searching for robustness of oscillatory behavior. Suggestions for TIPE topics, 2025-2026
Ongoing opportunities at Inria
Member of Education Board
Member of Editorial Board
‣ IEEE Open Journal of Control Systems (OJCS) ‣ IEEE Control Systems Society Conference Editoral Board Program Committees
‣ 25th International Symposium on Mathematical Theory of Networks and Systems (MTNS 2022) September 12-16, 2022), Bayreuth, Germany ‣ Dynamic Days (August 23-26, 2021), Nice, France ‣ Modelling Heterogeneous Populations with applications in Biology (May 17-18, 2021), Grenoble, France ‣ CSBio 2019 (4-7 December)International Conference on Computational Systems-Biology and Bioinformatics, Nice, France ‣ FOSBE 2019 (15-18 October) IFAC Conference on Foundations of Systems Biology in Engineering, Valencia, Spain ‣ JOBIM 2019 (2-5 July) Journées ouvertes de biologie informatique et mathématiques, Nantes, France ‣ MLCSB 2018 (17-18 December) International Symposium on Molecular Logic and Computational Synthetic Biology, Santiago, Chile ‣ JOBIM 2018 (3-6 June) Journées ouvertes de biologie informatique et mathématiques, Marseille, France Projects, ongoing
I am the coordinator of this new project MIC-ITMO Cancer - Aviesan, in partnership with Jeremie Roux and Diego Oyarzun, started in October 2022 (more information coming soon) ‣ InSync (2022 -- 2027) Intercellular coupling and synchronization between peripheral circadian clocks. I am the coordinator of this new ANR project (the French National Research Agency), in partnership with Franck Delaunay and Laurent Tournier, started in December 2022 ‣ Signalife (2012 -- 2020; 2020 -- 2024) Network for innovation on signal transduction pathways in life sciences. I am a member of the Scientific Board of this Labex (Laboratory of Excellence). Hosted by the University of Nice Sophia Antipolis, it is composed of about 50 local teams that study diverse aspects of signaling pathways. Labex funded by Investissements d'Avenir, 2011.
A project coordinated by Jeremie Roux and funded by Inserm - Plan Cancer, started in April 2018. ‣ ICycle (2017 -- 2021) Interconnection and feedback control of two cyclic modules in mammalian cells. I am the coordinator of this ANR project (the French National Research Agency), started in February 2017. ‣ SYNCHRO (2020 -- 2021) Coupling and synchronization of circadian oscillators in peripheral organs: mathematical modeling and analysis. Universite Cote d'Azur, Masters Environnes program. Co-ordinated with F. Delaunay (Institut de Biologie de Valrose - CNRS). ‣ LTSB (2018 -- 2019) Logical Tools for Systems Biology. I am the French part coordinator of this project funded by Partenariats Hubert Curien, PHC PESSOA, with Portuguese partner M.A. Martins at University of Aveiro. ‣ RESET (2012 -- 2016) Arrest and restart of the gene expression machinery in bacteria: from mathematical models to biotechnological applications. A project coordinated by Hidde de Jong and funded by Investissements d'Avenir, Bioinformatique. Started in October 2012, and runs for four years. ‣ GeMCo (2010 -- 2013) Model reduction, experimental validation, and control for the gene expression machinery in E. coli. I am the coordinator of this ANR funded project (the French National Research Agency). ‣ ColAge (2009 -- 2014) Natural and engineering solutions to the control of bacterial growth and aging. A joint research initiative (Inria Project Lab), co-funded by INRIA and INSERM (the French Institute for Medicine and Health), coordinated by Hugues Berry and Hidde de Jong. PhD students at Inria
Applications: Circadian clock and cell cycle 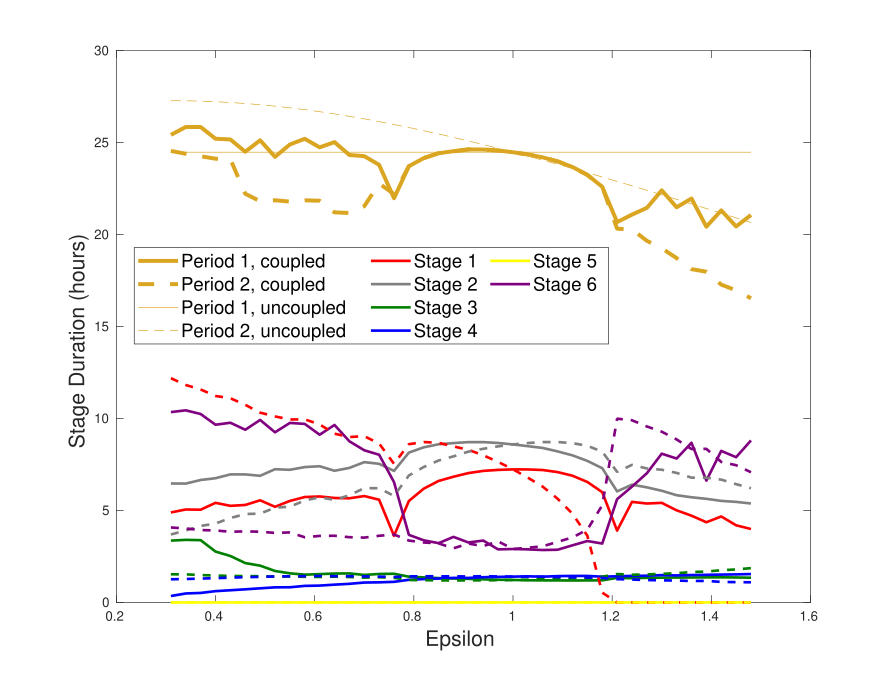 ‣ Synchronization among peripheral circadian clocks
(with O. Burckard, M. Teboul, F. Delaunay):
‣ Synchronization among peripheral circadian clocks
(with O. Burckard, M. Teboul, F. Delaunay): The intercellular interactions between peripheral circadian clocks, located in tissues and organs other than the suprachiasmatic nuclei of the hypothalamus, are still very poorly understood. Based on a piecewise linearization of our previously developed clock model, we suggest a segmentation of the circadian cycle into six stages, to help analyse synchronization dynamics between two clocks.
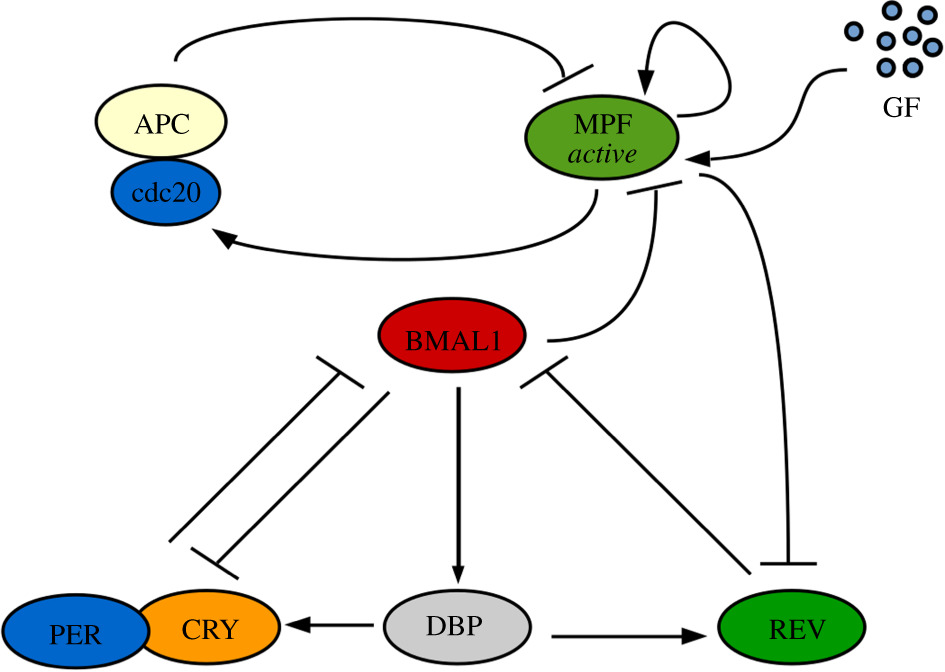 The mammalian circadian clock consists in a dynamical network of genes and proteins whose main regulatory mechanisms occur at the transcriptional level. We developed a transcription-based mathematical model centered on linear combinations of the clock controlled elements (CCEs): E-box, R-box and D-box. This model describes the dynamics of the proteins CLOCK:BMAL1, REV-ERBalpha, PER, CRY, and the complex PER:CRY, and it was calibrated with single-cell data on Rev-erb from Delaunay's Lab. In a second step, we investigated the dynamical interactions between the cell cycle and the circadian clock, by growth factors and glucocorticoids.
The mammalian circadian clock consists in a dynamical network of genes and proteins whose main regulatory mechanisms occur at the transcriptional level. We developed a transcription-based mathematical model centered on linear combinations of the clock controlled elements (CCEs): E-box, R-box and D-box. This model describes the dynamics of the proteins CLOCK:BMAL1, REV-ERBalpha, PER, CRY, and the complex PER:CRY, and it was calibrated with single-cell data on Rev-erb from Delaunay's Lab. In a second step, we investigated the dynamical interactions between the cell cycle and the circadian clock, by growth factors and glucocorticoids.
 ‣ Cyanobacteria circadian rhythms
(with M. Preto):
‣ Cyanobacteria circadian rhythms
(with M. Preto): In this work, we use several formalisms to model the Kai ABC oscillator, which is at the core of the cyanobacterial circadian clock. We start with a logical model, that contains the qualitative information available on the system. Building upon this structure, we then develop quantitative ``minimal'' models---with the smallest number of parameters and state variables---that are able to describe the dynamical properties observed in experiments. The resulting model successfully reproduces many of the defining properties of circadian rhythms, including the entrainment by the ``environment'', showing that it can synchronize with daily cycles, and it is robust to perturbations in the phase of oscillation. Applications: Apoptosis
Tumor cells of a clonal population exhibit multiple levels of heterogeneity, from gene expression to drug response. Cell-to-cell variability in cell death dynamics after treatment, is an emerging cause of drug resistance contributing to the reduced efficacies of cancer therapeutics (due to fractional killing). To study this problem, we are developing different approaches based on the modeling of the extrinsic apoptosis pathway, using both detailed models and compact core models.
Apoptosis is a form of programed cell death which enables the organism to remove unwanted or damaged cells. This is an essential biological function in a healthy living organism. The complex Nuclear Factor kB pathway interacts with the caspase cascade at the heart of apoptosis. I have worked on a Boolean model to study apoptosis regulation by the NFkB pathway. This is a system that exhibits bistability. Applications: other topics
 These are the genes responsible for establishing the anterior-posterior polarity
of segments in the embryo of the fruit fly. I have worked on the analysis of a Boolean model
of the segment polarity network, introducing
asynchronous updating rules, and other
methods that allow a more realistic analysis of discrete models with respect to the time scales of
the various regulatory processes (transcription, translation, or post-translational modifications).
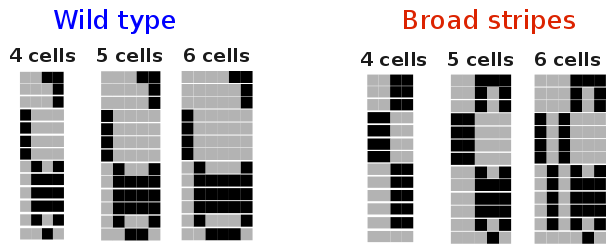
One can also study the effect of cell division on the robustness of the network (see figure).
These are the genes responsible for establishing the anterior-posterior polarity
of segments in the embryo of the fruit fly. I have worked on the analysis of a Boolean model
of the segment polarity network, introducing
asynchronous updating rules, and other
methods that allow a more realistic analysis of discrete models with respect to the time scales of
the various regulatory processes (transcription, translation, or post-translational modifications).
One can also study the effect of cell division on the robustness of the network (see figure). For the continuous model of the segment polarity network proposed by von Dassow et. al., we have fully characterized the feasible parameter space, as a hierarchy of intervals.
The binding of a ligand to a cell receptor triggers a sequence of biochemical reactions, that ultimately lead to a cell response (such as contraction, motility, proliferation). I am interested in the modeling of various stages in this process, from receptor-ligand binding, to cascades of protein activation, to cell signaling in the form of changes in the levels of cytosolic calcium, cAMP,... One of the goals would be to obtain validated models that help us in predicting and controlling the response of the cell to given stimulus. Regulation and control: Oscillatory systems
To analytically study the coupling of identical basic motifs under diffusive coupling, we represented a network of positive feedback loops as a piecewise linear system of differential equations. We analyse their capacity for synchronization and other emergent dynamical properties, such as the generation of new steady states. Motivated by the synchronization of circadian clocks in a cluster of cells, we next considered a network of N identical oscillators under diffusive coupling in a piecewise affine formalism. We investigate the effect of the topology of interactions in the network's dynamics and show that both all-to-all and one-to-all coupling topologies may introduce new stable steady states in addition to the expected periodic orbit. 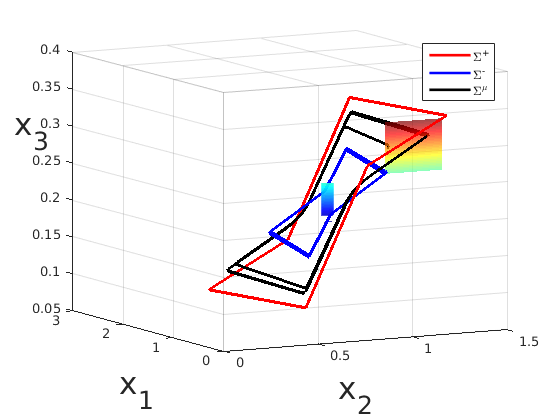 ‣ Periodic orbits in nonmonotonic negative feedback systems
(with C. Poignard and J.-L. Gouzé):
‣ Periodic orbits in nonmonotonic negative feedback systems
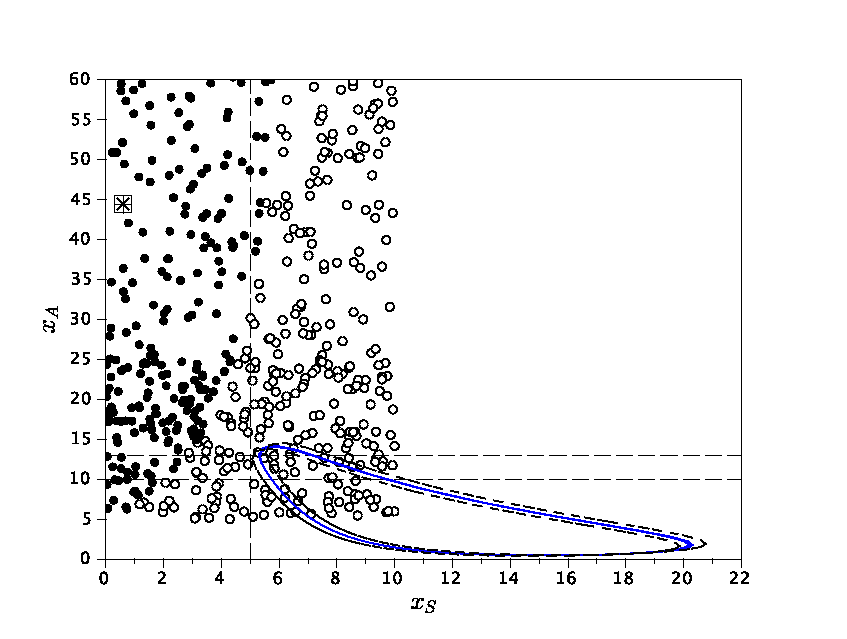
(with C. Poignard and J.-L. Gouzé): Stability and uniqueness of periodic orbits in nonlinear smooth systems are difficult properties to establish in general. We have proved existence of a periodic orbit for a class of negative feedback systems where the regulation function has a small nonmonotonic window. Then, under some symmetry assumptions on the parameters, we have also established uniqueness and stability of the periodic orbit, inside an invariant torus. The idea is to construct two piecewise affine systems which form interior and exterior bounds of the original system. Each of these bounding systems has a periodic orbit (blue and red curves in the figure) which generate an invariant torus for the trajectories of the original system (black curve). Moreover, we have computed an approximation of the period of the orbit in terms of the parameters and illustrated our results with examples from Arabidopsis and Neurospora circadian rhythms. Regulation and control: Boolean interconnections
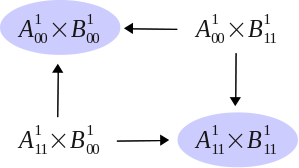 A biological network can be schematically described as an input/output Boolean module:
that is, both the states, the outputs and inputs are Boolean.
The interconnection of two Boolean modules can be characterized in terms of a new object,
called the asymptotic graph ,
whose nodes are cross-products of the attractors of each module.
We have shown that the attractors of the feedback interconnection of two Boolean modules
can be fully identified in terms of the attractors of the asymptotic graph.
Based on this result, a
model reduction technique
can be proposed, to predict the asymptotic dynamics of high-dimensional biological networks
through the computation of the dynamics of two isolated smaller subnetworks. More recently, we have refined the analysis of Boolean interconnections and introduced a probabilistic asymptotic graph.
A biological network can be schematically described as an input/output Boolean module:
that is, both the states, the outputs and inputs are Boolean.
The interconnection of two Boolean modules can be characterized in terms of a new object,
called the asymptotic graph ,
whose nodes are cross-products of the attractors of each module.
We have shown that the attractors of the feedback interconnection of two Boolean modules
can be fully identified in terms of the attractors of the asymptotic graph.
Based on this result, a
model reduction technique
can be proposed, to predict the asymptotic dynamics of high-dimensional biological networks
through the computation of the dynamics of two isolated smaller subnetworks. More recently, we have refined the analysis of Boolean interconnections and introduced a probabilistic asymptotic graph.
Boolean models often provide a good characterization of the qualitative dynamics of genetic networks. The state space of a Boolean model is finite, and its dynamics are fully described by an asynchronous transition graph. From the analysis of this graph, we identify families of operational interactions, that is, groups of interactions which are responsible for a given dynamical behaviour of the system. See application to the apoptosis network. Regulation and control: other topics
Gene expression can impact metabolic levels through changes in enzyme concentration and, conversely, metabolic species can influence gene transcription and hence modulate enzyme synthesis. To analyze these interactions, we have studied an unbranched metabolic chain (described by classical kinetic equations) with one metabolite acting as a global regulator of enzyme expression (described by PWA systems). Under the hypothesis that metabolic reactions happen in a faster time scale when compared to gene transcription or translation, we develop geometric criteria to characterize the equilibria (mono- or bi-stability) or possible oscillations of the network. 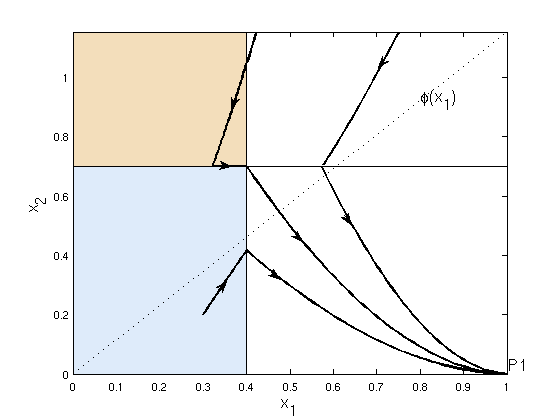
The concentrations of proteins and mRNAs in genetic regulatory networks are often characterized as ``strongly'' or ``weakly'' expressed. To deal with this type of measurements we explore a qualitative method to control piecewise affine differential systems, by considering systems whose outputs and inputs are of a qualitative form. The control laws are piecewise constant functions in each region and in time, and are only allowed to take three qualitative values corresponding to no control (u=1), high synthesis rates (u=umax) or low synthesis rates (u=umin). An application is to control the bistable switch system to either of its steady states.
In the context of project GeMCo, we developed a minimal synthetic gene circuit, that describes part of the gene expression machinery in Escherichia coli, and enables the control of the growth rate of the cells during the exponential phase. The model is a piecewise non-linear system, its dynamics and the bifurcation diagram with respect to the input are studied, and we obtain an analytic expression of the growth rate during the exponential phase as function of the input. Some problems include the identifiability of the parameters of the model supposing noisy measurements.
Many signaling pathways eventually trigger transcription of groups of genes. But, conversely, the signaling pathway may be regulated by gene expression patterns. We propose a simple model for such a regulatory mechanism, exploring the idea that the dynamics of a signal transduction pathway is must faster than the dynamics of gene transcription/translation.
Zero-deficiency chemical networksare a class of nonlinear systems which model general biochemical networks with mass-action kinetics. The formalism was first introduced and studied by M. Feinberg, F. Horn and R. Jackson. In my thesis I designed globablly asymptotically convergent observers for this class of systems, where other standard observers (eg. Kalman filters) may fail. I have extended the analysis of zero-deficiency networks to the case of time-dependent kinetic parameters - these are interpreted as inputs into the system. Such system satisfies an input-to-state stability (ISS) property, which guarantees robustness with respect to small perturbations in the kinetic parameters, such as temperature fluctuations, or various external factors and stimuli. |