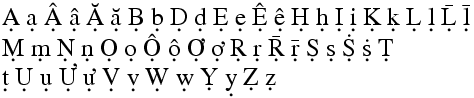
This page contains the description of the following commands
\d,
\D,
\dag,
\dagger,
\daleth,
\dasharrow,
\dashbox,
\dashleftarrow,
\dashline,
\dashrightarrow,
\dashv,
\date,
\day,
\dbinom,
\@dblarg,
\dblfigrule,
\dblfloatpagefraction,
\dblfloatsep,
\dbltextfloatsep,
\dbltopfraction,
\dbltopnumber,
\ddag,
\ddagger,
\ddddot,
\dddot,
\ddot,
\ddots,
\deadcycles,
\DeclareErrorFont,
\DeclareFixedFont,
\DeclareFontEncoding,
\DeclareFontEncodingDefaults,
\DeclareFontFamily,
\DeclareFontShape,
\DeclareFontSubstitution,
\DeclareMathAccent,
\DeclareMathAlphabet,
\DeclareMathOperator,
\DeclareMathDelimiter,
\DeclareMathRadical,
\DeclareMathSizes,
\DeclareMathSymbol,
\DeclareMathVersion,
\DeclareOldFontCommand,
\DeclareOption,
\DeclareOptionX,
\DeclarePreloadSizes,
\DeclareRobustCommand,
\DeclareSizeFunction,
\DeclareSymbolFont,
\DeclareSymbolFontAlphabet,
\DeclareTextAccent,
\DeclareTextCommand,
\DeclareTextCommandDefault,
\DeclareTextComposite,
\DeclareTextCompositeCommand,
\DeclareTextFontCommand,
\DeclareTextSymbol,
\DeclareTextSymbolDefault,
\declaretopic,
\def,
\default@ds,
\defaulthyphenchar,
\defaultskewchar,
\define@boolkey,
\define@boolkeys,
\define@choicekey,
\define@choicekeys,
\define@cmdkey,
\define@cmdkeys,
\define@key,
\definecolor,
\DefineShortVerb,
\DefineVerbatimEnvironment,
\deg,
\delcode,
\delimiter,
\delimiterfactor,
\delimitershortfall,
\delta,
\Delta,
\delpresetkeys,
\delsavekeys,
\@depth,
\depthof,
\det,
\detokenize,
\dfrac,
\dh,
\DH,
\diagup,
\diagdown,
\diamond,
\Diamond,
\diamondsuit,
\DifferentialD,
\digamma,
\dim,
\dimen,
\dimen@,
\dimen@i,
\dimen@ii,
\dimendef,
\ding,
\discretionary,
\displayindent,
\displaylimits,
\displaystyle,
\displaywidowpenalties,
\displaywidowpenalty,
\displaywidth,
\div,
\divide,
\divideontimes,
\dj,
\DJ,
\do,
\documentclass,
\dot,
\doteq,
\Doteq,
\doteqdot,
\dotfill,
\dotplus,
\dots \dotsc \dotsb \dotsi \dotsm,
\dottedline,
\doublecap,
\doublecup,
\doublehyphendemerits,
\doublerulesep,
\downarrow,
\Downarrow,
\downdownarrows,
\downharpoonleft,
\downharpoonright,
\dospecials,
\dp,
\drawline,
\dump,
and environments
description,
displaymath,
document.
The \d command generates a dot-under accent. The translation of
\d A \d a \d{\^A} \d{\^a} \d{\u A} \d{\u a} \d B \d b \d D \d d \d E \d e
\d{\^E} \d{\^e} \d H \d h \d I \d i \d K \d k \d L \d l \d{\=L} \d{\=l}
\d M \d m \d N \d n \d O \d o \d{\^O} \d{\^o} \d{\H O} \d{\H o}
\d R \d r \d{\=R} \d{\=r} \d S \d s \d{\.S} \d{\.s} \d
\d t \d U \d u \d {\H U} \d{\H u} \d V
\d v \d W \d w \d Y \d y \d Z \d z
is
Ạ ạ Ậ ậ Ặ ặ Ḅ ḅ Ḍ ḍ Ẹ ẹ Ệ ệ Ḥ ḥ Ị ị Ḳ ḳ Ḷ ḷ Ḹ ḹ Ṃ ṃ Ṇ ṇ Ọ ọ Ộ ộ Ợ ợ Ṛ ṛ Ṝ ṝ Ṣ ṣ Ṩ ṩ Ṭ ṭ Ụ ụ Ự ự Ṿ ṿ Ẉ ẉ Ỵ ỵ Ẓ ẓ
Preview 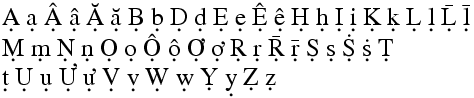
HTML characters: Ạ ạ Ậ ậ Ặ ặ Ḅ ḅ Ḍ ḍ Ẹ ẹ Ệ ệ Ḥ ḥ Ị ị Ḳ ḳ Ḷ ḷ Ḹ ḹ Ṃ ṃ Ṇ ṇ Ọ ọ Ộ ộ Ợ ợ Ṛ ṛ Ṝ ṝ Ṣ ṣ Ṩ ṩ Ṭ ṭ Ụ ụ Ự ự Ṿ ṿ Ẉ ẉ Ỵ ỵ Ẓ ẓ
The \D command generates a ring-under accent. The translation of \D A \D a is Ḁ ḁ or Ḁ ḁ.
Same as \dagger, in text mode.
The \dagger command is valid only in math mode. It generates a binary operator: <mo>†</mo> (Unicode U+2020 †). See description of the \pm command.
The \daleth command is valid only in math mode. It generates <mi>ℸ</mi> (Unicode U+2138, ℸ)
The \dasharrow command is valid only in math mode. It generates <mi>⤏</mi> (Unicode U+290F, ⤏)
You can say \dashbox{dim}(xd,yd)[pos]{text} inside a picture. See description of the picture environment for the syntax of the (xd,yd) part (the size of the box), and some examples. It is like \framebox command, in that it produces a rectangular box whose lower-left edge is at the current position, with dimension (xd,yd), that contains text that is justified according to [pos], which can be one of l, r, t, b, (left, right, top, bottom) or a combination of the two. The difference is that the frame is dashed, the length of the dashes being {dim}.
The \dashleftarrow command is valid only in math mode. It generates <mi>⤎</mi> (Unicode U+290E, ⤎)
The \dashline command takes as argument an optional [stretch] parameter (an integer between -100 and infinity), if omitted the value of a global variable will be used. It takes an argument {dashlength} that is the length of the dash to be used, and an optional [dashdotgap] parameter; these two parameters are used by \dottedline to construct the dash. After that, the command takes N (at least two) pairs of coordinates (x,y) these define line segments for which a dashline should be drawn.
Example
\begin{picture}(70,22)(0,-2)
\dashline{3}[0.7](0,18)(63,18)
\thicklines
\dashline{3}(0,13)(63,13)
\dashline[-30]{3}(0,8)(63,8)
\dashline[+15]{3}(0,4)(63,4)
\dashline[+30]{3}(0,0)(63,0)
\end{picture}
Translation: not available. Can be used only in a picture environment.
The \dashrightarrow command is valid only in math mode. It generates <mi>⤏</mi> (Unicode U+290F, ⤏)
The \dashv command is valid only in math mode. It generates a relation symbol (reversed \vdash): <mo>⊣</mo> (Unicode U+22A3, ⊣). See description of the \le command.
The translation of \date{today} is <date>today</date>. In fact, the command is defined by \def\date#1{\xmlelt{date}{#1}}
When you say \day=904, you put 904 in the \day counter, but nothing special happens. This counter is initially set to the numbers of days elapsed in the current month. So that \the\day may be translated as 7 on the seventh of April 2004. (See scanint for details of argument scanning). (See \time for an example.)
The \dbinom command is valid only in math mode. It could be defined as \def\dbinom{\genfrac(){0pt}0}. Said otherwise, it takes two arguments, puts them one over the other, in display style, and puts parentheses around. See \binom.
Consider the following example
\def\auxfoo[#1]#2{Opt=#1 Req=#2}
\def\fooA{\ifnextchar[{\auxfoo}{\auxfoo[xx]}}
\newcommand\fooB[2][xx]{Opt=#1 Req=#2}
\def\fooC{\@dblarg\auxfoo}
\let\@nx\noexpand
\edef\fooD{\@nx\@dblarg\expandafter\@nx\csname\string\fooB\endcsname}
\newcommand\fooE[2][\@dblarg]{Opt=#1 Req=#2}
Here \fooA is a macro that takes an optional argument and a required one. If the optional argument is omitted, the value xx will be used instead. Command \fooB does the same. Command \fooC is like \foo but the default value of the optional argument is the required one. Another use of \@dblarg can be found in \fooD. Note how this calls the auxiliary function associated to \fooB. This construction does not work in Tralics because there is no auxiliary function. On the other hand, Tralics version 2.13.1 understands the definition of \fooE as to be the same as \fooD.
The command \dblfigrule behaves like \relax, in LaTeX it can be redefine to produce a rule between a float and text in two columns.
Parameters that control position of floats in double column mode. Unused by Tralics. See \intextsep.
Parameters defined by Tralics but not used, see \intextsep.
Same as \ddagger, in text mode. The translation of $\dagger$ -- $\ddagger$ -- \dag{} -- \ddag is
<formula type='inline'>
<math xmlns='http://www.w3.org/1998/Math/MathML'>
<mo>†</mo>
</math>
</formula>
–
<formula type='inline'>
<math xmlns='http://www.w3.org/1998/Math/MathML'>
<mo>‡</mo>
</math>
</formula>
– † – ‡
Preview: 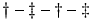 (see also here).
(see also here).
The \ddagger command is valid only in math mode. It generates a binary operator (double dagger): <mo>&ddager;</mo> (Unicode U+2021, ‡). See description of the \pm command.
Maximum number of multicolumn floats on top of a page. Not used by Tralics. See \intextsep.
The \ddddot command puts a 4-dot accent over a kernel. See the \acute command.
The \ddddot command puts a 3-dot accent over a kernel. See the \acute command.
The \ddot command puts a double dot accent over a kernel. It works only in math mode. Do not confuse with \" (see \"). See also the \acute command.
The \ddots command is valid only in math mode. It generates a miscellaneous symbol (diagonal dots): <mo>⋱</mo> (Unicode U+22F1, ⋱). See description of the \ldots command.
The integer variable \deadcycles is set to zero after \shipout, incremented just before \output. When TeX evaluates the \end command and the values of \deadcycles is not zero, it exercises the page builder, hoping \shipout being called; the \end token is evaluated again (note that LateX redefines the \end token). Whenever \deadcycles becomes more than \maxdeadcycles, an error is signaled, and the call to the user \output routine is replaced by a call to the default \output routine (that will call \shipout).
In Tralics, you can assign any value to \deadcycles, nothing happens. You can consult the value, you will always see zero.
You can say \DeclareMathOperator\foo{bar} or \DeclareMathOperator*{\xfoo}{bar}. This is the same as \newcommand*\foo{\operatorname{bar}} or \newcommand*{\xfoo}{\operatorname*{bar}}. This command can be used everywhere (LaTeX requires it to be placed in the preamble). See description of the \operatorname command.
Inside a class or package file, you can say \DeclareOption{foo}{bar}. This remembers that the value of foo is bar. Instead of `bar', there should be a sequence of commands that modify the environment (typesetting is forbidden, because the command is executed in the preamble). The command could set a boolean value, set a dimension register, load auxiliary files, etc. It can also add tokens to the document class hook (in other words, the action may depends on subsequently loaded packages). No error is signaled if the command is used out of context, or if the option is already defined. If you say \ExecuteOptions{x,y}, the code associated to options x and y is executed. Typically, each package contains such a line, given a default values for all the booleans, registers, etc. The package contains also \ProcessOptions. The effect is to execute the code of the user-declared options. The order of evaluation is (by default), the order in which options are declared in the package. If options foo and bar set the same boolean to different values, then the user should specify only one of them. In some cases, the code of an option sets a boolean, and after \ProcessOptions there is some code that uses the boolean value (the idea being that the boolean is not modified any more).
You can say \DeclareOption*{bar}. This means that the package
recognises any option, and applies `bar' to it; instead of these three
characters, you should use something more sensible, for instance
\inputencoding{\CurrentOption}. Here \CurrentOption
contains the name of the current options, and the other command is defined by
the package (of the form: input a file whose name depends on the option).
 See also
\ExecuteOptions.
See also
\ExecuteOptions.
The xkeyval package provides an extension, of the form \DeclareOptionX{foo}{bar=#1}. Normally #1 is empty, but is gee, if the package is loaded with foo=gee.
Translation of \declaretopic{A}{B} is <topic num='A'><t_titre>B</t_titre></topic>. In old version of Tralics you could put the following lines in the configuration file
att_topic_num = "Num" xml_topic_name = "Topic" xml_topic_title = "Title"
This changed the translation. In the current version, the \declaretopic command (as well as the names of the XML elements and attributes) is defined in the package file for the raweb.
The \DeclareRobustCommand behaves like \newcommand. However, if the command is already defined, nothing happens. In LaTeX, the result is a robust command (something that is not implemented in Tralics), and redefining the command prints a warning in the log file.
When you say \def\foo{bar}, you construct a command whose expansion is bar (three tokens, of \catcode letter). When you say \def\xfoo#1#2{#2+#1} you construct a command \xfoo whose expansion reads two tokens lists (say argument1 and argument2), and produces a token list formed by argument2, a plus sign (a character of \catcode12) and argument1. When you say \def\zfoo#1\bar#2#{#2+#1} the \zfoo command expands as \xfoo, but it reads its arguments differently: the first argument is everything before the token \bar and the #{ after #2 means that the second argument is delimited by an opening brace.
In the case of \zfoo both arguments are delimited. They are defined as the shortest token lists (properly nested with respect to braces) that match the specification. In the case \zfoo 1\bar2\bar3{4}, the first argument is 1, the second argument is 2\bar3, and the tokens {4} are interpreted later. In the case of an undelimited argument, the value is the first non-blank token, unless this token is an opening brace, case where the argument is the token list that starts with this brace. In both cases, if the argument constructed in this way is a token list that starts with an open brace, and ends with a closing brace, and remains nested if we remove the braces, they are removed. For instance, \xfoo12, \xfoo1 {2}, \xfoo{1} 2, \xfoo{1} {2} are all equivalent. Note that \zfoo 1\bar2{3} and \zfoo{1}\bar {2}{3} are not equivalent, the first argument is 1 in each case, but the second argument is 2 (first case) or empty (second case).
In the case \def\foo#1{\def\bar##1{#1##1}}, a macro \foo is defined, it takes one argument, and its expansion is \def\bar#1{foo-arg#1}, where foo-arg is the argument of \foo. In the body of \foo, the sequence ## is replaced by #.
Instead of # you can use anything equivalent to it.
For instance \let\foo# \def\A\foo1\foo2{\foo1}.
In the case of \let\foo# \def\B{#\foo}\def\C{\foo#},
the \B macro
takes no argument, its body contains a single token, whose value
is equivalent to macro parameter character #
. In fact, the token
in \B is \foo, and it has nothing to do with a sharp
sign, it is just a command whose current meaning is the same as that of a character
of catcode 6, and, in general, only the sharp sign matches this
definition. On the other hand, the token in \C is a
sharp sign token.
The previous code is completely equivalent to \def\B{\foo}\def\C{##}\let\foo#.
This is the command that handles unknown class or package options. The default value is \OptionNotUsed.
When you say \defaulthyphenchar=74, then TeX will use 74 for the \hyphenchar of every new font it loads. This is not used in Tralics. (See scanint for details of argument scanning).
When you say \defaultskewchar=73, then TeX will use 73 for the \skewchar of every new font it loads. This is not used in Tralics. (See scanint for details of argument scanning).
These commands are provided by the keyval package.
This command defines a short-hand character for verbatim code. The command takes one argument that is one-character command, for instance \DefineShortVerb{\+}. After that, +foo+ is the same as \verb+foo+. For more details, see catcode 16.
You can say\DefineVerbatimEnvironment{myname}{tname}{list} This is equivalent to
\let\myname = \tname
\let\endmynane = \endtname
\def\myname@hook{list}
If the second argument is one of verbatim, Verbatim or lst@verbatim, then this defines a verbatim environment. In the first case, you have a simple verbartim environment, and the value of the last argument is ignored. Moreover, all characters that are on the same line as the \begin{myname} are ignored. In the other case, an optional argument is read (when \begin{myname} is followed, on the same line, by an open bracket that may be preceded by blank space). All characters following the optional argument are lost.
In the second case, Tralics merges the value of the hook, (i.e., of \myname@hook) and the optional argument, and interprets this as an association list (see description of the Verbatim command). The recognized keys are: number (in this case, all lines of the verbatim environment are numbered), firstnumber (this allows to specify the number associated to the first line), pre=xx (in this case, the command \FV@pre@xx is executed before the verbatim material, and \FV@post@xx is excluded just after); you can also say style=yy, case where \FV@style@yy is executed just after \FV@pre@xx).
In the case where the name is lst@verbatim, then Tralics does not parse the optional arguments (as a side effect, lines will not be numbered); it uses lst for xx and yy.
The \deg command is valid only in math mode. Its translation is a math operator of the same name: <mo form='prefix'>deg</mo>. For an example see the \log command.
When you say \delcode13 12, you change the delimiter code of the character number 13 to the value 12. See scanint for details of how numbers are read. The first integer must be a valid character code (between 0 and 255, in TeX, 216-1 in Tralics), and the second must be less than 2 power 24. See \spacefactor. If you say \delcode`x="123456 then x can be used as delimiter in math mode. The small variant is defined by 123, the large variant by 456. (here 123 means: family one, position hex23). A negative value is allowed, and the character cannot be used as a delimiter. If one part is zero, it is omitted. If the \delcode is zero, neither variant will be used: this produces an empty delimiter. In TeX, most \delcode values are -1, but \delcode`.=0. In Tralics, the \delcode table is initialized to zero, and unused.
The \delimiter command reads a 27-bit integer (see scanint for details). If you say \def\langle{\delimiter"426830A }, then the following happens. In case where \langle is preceded by \left or \right, the result is as if you had enter a character whose \delcode were "26830A (split as 268 and 30A), otherwise as if you hand entered a character whose \mathcode were "4268, i.e. class 4, family 2, position 68. This is unused in Tralics.
When you say \delimiterfactor=902, then TeX will use this value (divided by 1000) as factor for computing the size of a delimiter: if we have a formula of height plus depth 30pt, applying this factor gives 27pt, so that delimiters will be at least 27pt tall. This parameter is set to 901 in LaTeX, it is ignored by Tralics. (See scanint for details of argument scanning).
When you say \delimitershortfall=5pt, then TeX will use delimiters whose size are at least the size if we have a formula of height plus depth 100pt, delimiters will be at least 95pt tall (see also \delimiterfactor above) This parameter is set to 5pt in LaTeX, it is ignored by Tralics. (See scandimen for details of argument scanning).
These commands are provided by the keyval package.
The \delta command is valid only in math mode. It generates a Greek letter: <mi>δ</mi> (Unicode U+3B4, δ). See description of the \alpha command.
The \Delta command is valid only in math mode. It generates an uppercase Greek letter: <mi>Δ</mi> (Unicode U+394, Δ). See description of the \alpha command.
This command expands to depth. Do not modify it.
This command is defined by the calc package but not implemented in Tralics.
This is an environment in which you can puts items. See description of the \item command.
The \det command is valid only in math mode. Its translation is a math operator of the same name: <mo form='prefix' movablelimits='true'>det</mo>. For an example see the \log command.
The command \detokenize reads a token
list and
detokenizes it; said otherwise the token list is converted into a character
list, of category code 12 (except for space).
This
command behaves like \the, in that the resulting token list is not
expanded, even in a \edef or \write.
See also
\glueshrink,
where we explain how to use this command in order to compare the
result of \the and a constant character string.
In the example that follows, the command \addid takes an argument
of the form cite:foo_bar^gee and adds an attribute pair to the
current element, with value foo_bar^gee. The
\detokenize command replaces the funny math-only characters
(hat and underscore) by normal characters. The \getid command
strips the prefix; you cannot say \def\getit cite:#1\\{#1},
because the category codes are wrong; changing category code of the letters
c, i, t and e is possible, but tricky since some of them appear in the command
name (see for instance \strip@pt).
We use here \detokenize.
\expandafter\def\expandafter\getid \detokenize{cite}:#1\\{#1}
\def\expandid#1{\expandafter\getid \detokenize{#1}\\}
\def\addid#1{\XMLaddatt{user-id}{\expanduserid{#1}}}
The \dfrac command is display style fraction. It is like \frac, but the result has a scriptlevel='0' attribute. See the \frac command.
This translates to ð or ð for \dh and Ð or Ð for \DH. For more info see the latin supplement characters.
The \diagdown command is valid only in math mode. It generates <mi>∖</mi> (Unicode U+2216, ∖).
The \diagup command is valid only in math mode. It generates <mi>&∕</mi> (Unicode U+2215, ∕).
The \diamond command is valid only in math mode. It generates a binary operator: <mo>⋄</mo> (Unicode U+22C4, ⋄). See description of the \pm command.
The \Diamond command is valid only in math mode. It generates a miscellaneous symbol: <mo>⋄</mo> (Unicode U+22C4, ⋄). See description of the \ldots command. In Tralics, there is no difference between \diamond and \Diamond.
The \diamondsuit command is valid only in math mode. It generates a miscellaneous symbol (diamond suit, a bit larger than the \diamond operator): <mo>♦</mo> (Unicode U+2666, ♦). See description of the \ldots command.
The \DifferentialD command is valid only in math mode. It generates the differential d operator <mo>ⅆ</mo> (Unicode U+2146, ⅆ).
The \digamma command is valid only in math mode. It generates <mo>ϝ</mo> (Unicode U+3DD, ϝ).
The \dim command is valid only in math mode. Its translation is a math operator of the same name: <mo form='prefix'>dim</mo>. For an example see the \log command.
When you say \dimen13 12pt, you change the value of the dimension register number 13 to the value 12pt. See scanint for details of how integers are read, and scandimen for dimensions. The integer must be a valid register number (between 0 and 255 in TeX, 1023 in Tralics). The previous example can also be written as \dimen`\^^M=4\parindent, in case \parindent is 3pt.
The\dimen@, \dimen@i \dimen@ii commands are scratch dimensions; they are aliases (defined via \dimendef) to \dimen0, \dimen1 and \dimen2. In order to save stack space, assignment to odd registers should be global, assignments to even registers should be local.
When you say \dimendef\foo=13, you make \foo an alias for \dimen13. See scanint for details of how the number 13 is read; it has to be a valid register number (between 0 and 255, 1023 in Tralics). The command \newdimen uses \dimendef for defining the command associated to the dimension.
You can put the prefix \global before \dimendef.
The \ding command is explained in the page concerning Dingbats characters.
If you say \discretionary{f-}{fi}{ffi}, then TeX will translate this as `ffi', except when it has to hyphenate the word. In the case, the first line will contains `f-' on the right and the second line will contain `fi' on the left. Since Tralics does no hyphenation, the translation is always `ffi'. Thus the \discretionary command is ignored, as well as its first two arguments. On the other hand, in a case like \discretionary{}{}{\huge foo}, the font change is local.
The content of a displaymath environment is translated in display math mode. The result is a <formula> element. It behaves much like the equation environment except that the equation counter is unchanged. See also the split environment. See also the equation environment.
Whenever TeX is about to typeset a display formula, it puts in \displayindent the desired indentation (depending on \parshape or hanging indentation). You may say \displayindent=5pt, or whatever. When the display is finished, the value is read. (See \predisplaysize for further details). This parameter is ignored by Tralics. (See scandimen for details of argument scanning).
The \displaylimits command is valid only in math mode. It describes how indices should be positioned. See \nolimits for details.
The \displaystyle command is valid only in math mode. It changes the current style to display. The result is something like <mstyle displaystyle="true" scriptlevel="0">...</mstyle> and one problem is to find the argument of the MathML element. In fact, Tralics understands the declaration only at the beginning of a group, as in the example that follows.
In Version 2.0, the style can appear anywhere, but an attribute is added the current block, so that, as the example shows, the letter x uses the same style as what follows.
${\frac12}{x\displaystyle\frac 12}
{x\textstyle\frac 12}{x\scriptstyle\frac 12}{x\scriptscriptstyle\frac 12} \qquad
{x\displaystyle a}+{x\textstyle a}+{x\scriptstyle a}+{x\scriptscriptstyle a}\qquad
\frac{x\displaystyle a}{x\textstyle b}+\frac{x\scriptstyle a}{x\scriptscriptstyle b}$
Translation
<formula type='inline'> <math xmlns='http://www.w3.org/1998/Math/MathML'> <mrow> <!-- no style --> <mfrac><mn>1</mn> <mn>2</mn></mfrac> <!-- {x\displaystyle \frac 12} --> <mstyle scriptlevel='0' displaystyle='true'> <mrow><mi>x</mi><mfrac><mn>1</mn> <mn>2</mn></mfrac></mrow></mstyle> <!-- {x\textstyle \frac 12} --> <mstyle scriptlevel='0' displaystyle='false'> <mrow><mi>x</mi><mfrac><mn>1</mn> <mn>2</mn></mfrac></mrow></mstyle> <!-- {x\scriptstyle \frac 12} --> <mstyle scriptlevel='1' displaystyle='false'> <mrow><mi>x</mi><mfrac><mn>1</mn> <mn>2</mn></mfrac></mrow></mstyle> <!-- {x\scriptscriptstyle \frac 12} --> <mstyle scriptlevel='2' displaystyle='false'> <mrow><mi>x</mi><mfrac><mn>1</mn> <mn>2</mn></mfrac></mrow></mstyle> <mspace width='2.em'/> <!-- {x\displaystyle a} --> <mstyle scriptlevel='0' displaystyle='true'> <mrow><mi>x</mi><mi>a</mi></mrow></mstyle> <mo>+</mo> <!-- {x\textstyle a} --> <mstyle scriptlevel='0' displaystyle='false'> <mrow><mi>x</mi><mi>a</mi></mrow></mstyle> <mo>+</mo> <!-- {x\scriptstyle a} --> <mstyle scriptlevel='1' displaystyle='false'> <mrow><mi>x</mi><mi>a</mi></mrow></mstyle> <mo>+</mo> <!-- {x\scriptscriptstyle a} --> <mstyle scriptlevel='2' displaystyle='false'> <mrow><mi>x</mi><mi>a</mi></mrow></mstyle> <mspace width='2.em'/> <!-- \frac{x\displaystyle a}{x\textstyle b} --> <mfrac> <mstyle scriptlevel='0' displaystyle='true'> <mrow><mi>x</mi><mi>a</mi></mrow></mstyle> <mstyle scriptlevel='0' displaystyle='false'> <mrow><mi>x</mi><mi>b</mi></mrow></mstyle> </mfrac> <mo>+</mo> <!-- \frac{x\scriptstyle a}{x\scriptscriptstyle b} --> <mfrac> <mstyle scriptlevel='1' displaystyle='false'> <mrow><mi>x</mi><mi>a</mi></mrow></mstyle> <mstyle scriptlevel='2' displaystyle='false'> <mrow><mi>x</mi><mi>b</mi></mrow></mstyle> </mfrac> </mrow> </math> </formula>
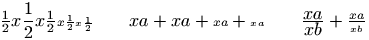 (see also here).
(see also here).
Whenever TeX is about to typeset a display formula, it puts in \displaywidth the current line width. You may say \displayindent=5pt, or whatever. When the display is finished, the value is read. (See \predisplaysize for further details). This parameter is ignored by Tralics. (See scandimen for details of argument scanning).
This is an extension defined by ε-TeX. See \widowpenalties for syntax and usage.
When you say \displaywidowpenalty=99, then TeX will use 99 as penalty for a line that starts a page and is followed by a display equation, when it computes optimal page breaks. Unused by Tralics. (See scanint for details of argument scanning).
The \div command is valid only in math mode. It generates a binary operator (division symbol, horizontal rule with two dots): <mo>÷</mo> (Unicode U+F7, ÷). See description of the \pm command. Outside math mode, you should say ÷ or \textdiv.
If you say \global\divide\count0 by 2, the value of \count0 is globally divided by 2. The keyword by is optional. Instead of \count0 you can put any variable that remembers an integer, a dimension, a glue, or a muglue (in reality, the same quantity that can be put after \advance); after the optional by a number is required (and an number is an integer in this context). You should not divide by zero.
The \divideontimes command is valid only in math mode. It generates <mo>⋇</mo> (Unicode U+22C7, ⋇).
This is the Unicode character U+111, đ for \dj and U+110, Đ for \DJ. For more info see the extended latin characters.
The \do command is used by \dospecials whose definition is given below, and maybe other commands for loops. It is set to \noexpand by \begin{document}. It is used as delimiter by \@whilenum, \@whiledim, \@for and \@tfor. In a certain number of cases, \do is the same as \@makeother and the effect of \dospecials is to change the category codes of most special characters to non-special (before using this command, please check that it can be reverted; a typical use is inside a verbatim environment, and a special code is used to test the end of the environment). The \@sanitize command make all these characters non-special, it is used for instance by the \index command (in LaTeX, if you say \index{\foo}, the \foo command is not evaluated, but written on the file; it will be evaluated later when LaTeX reads the sorted index; in Tralics nothing is written on a file). As you can notice, braces are in one list, but not the other, this has as effect that when \index reads its argument the braces are still argument delimiters!
\def\dospecials{\do\ \`do\\\do\{\do\}\do\$\do\&\do\#\do\^\do\_\do\%\do\~}
\def\@sanitize{\@makeother\ \@makeother\\\@makeother\$\@makeother\&%
\@makeother\#\@makeother\^\@makeother\_\@makeother\%\@makeother\~}
The document environment is special. It can be used only once (since the end of the environment indicates the end of the job). It should only be used at level zero (outside any group), because definitions inside the document environment are considered to be outside a group (there is no need to save old definitions, because restoring them at the end of the job is useless).
After that, the command \AtBeginDocument is made equivalent to \@firstofone, and scheduled to be equivalent to \@notprerr (which provokes an error), and the tokens saved by \AtBeginDocument are inserted (redefinition of \AtBeginDocument takes place after these tokens have been evaluated). An example is given in the description of \AtBeginDocument.
When \end{document} is sensed, all files are closed, including the current file. A special \end{document} command is inserted; all tokens inserted by \AtEndDocument are inserted, and this command is made equivalent to \@firstofone.
The purpose of the special \end{document} is to keep everything in sync. It is not really needed (nothing catastrophic happens if you forget the \end{document} declaration; you might see a line of the form: Save stack +14 -11 indicating that some closing braces or \end commands are missing.)
The \documentclass command can be used only once before the \begin{document}. It takes one argument, say cls preceded by an optional argument (say opts), followed by an optional argument (ignored). The parameter cls defines the class used by Tralics, (except that DTD is defined by the first \documentclass seen in the file, and it can be hidden in a comment).
In the case where the optional argument opts contains useallsizes then Tralics uses a lot of font sizes in the output, otherwise, it uses only three of them, see \rm. If it contains french, then French will be the default language. If it contains english, then English will be the default language. Note that the default language is English (except for the RA2002). If it contains leadingpart or leadingchapter then the toplevel section is assumed to be \part or \chapter.
In the case where the required argument cls contains book, then \part is assumed to be the leading section, and if its contains report, then \chapter is assumed to be the leading section. In all other cases, \section is the leading section.
The \dot command puts a dot accent over a kernel. It works only in math mode. Do not confuse with \. (see \.). See also the \acute command.
The \doteq command is valid only in math mode. It generates a relation symbol (equals sign with a dot above): <mo>≐</mo> (Unicode U+2250, ≐). See description of the \le command.
The \Doteq command is valid only in math mode. It generates <mo>≑</mo> (Unicode U+2251, ≑).
The \doteqdot command is valid only in math mode. It generates <mo>≑</mo> (Unicode U+2251, ≑).
Translation of \dotfill is <dotfill>.
The \dotplus command is valid only in math mode. It generates <mo>∔</mo> (Unicode U+2214, ∔).
The \dots command is valid in math mode and text mode. It generates three dots or <mo>⋯</mo>. (Unicode U+22EF, ⋯) See description of the \qquad command. The four commands \dotsc, \dotsb \dotsi and \dotsm are defined by ams-math. In Tralics, they are all equal to \cdots. The translation is the same as that of \dots.
The \dottedline takes a dot specification [dotchar]{dotgap} and a list of N (at least two) points (x,y). A dotted line is drawn between each pair of coordinates, using an inter-dot gap as specified, and a little square, unless the optional parameter is given, case where it indicates the character to use. Example:
\begin{picture}(150,15)(0,0)
\thicklines
\dottedline{2}(0,10)(70,10)
\dottedline[$\bullet$]{3}(0,5)(70,5)
\dottedline[$\diamond$]{4}(0,0)(70,0)
\end{picture}
Translation is not available. There is a bug somewhere; moreover, math formulas are not allowed by Tralics in this context. Can be used only in a picture environment.
The \doublecap command is valid only in math mode. It it is an alias for \Cap, translates to <mo>⋒</mo>. (Unicode U+22D2, ⋒).
The \doublecup command is valid only in math mode. It it is an alias for \Cup, translates to <mo>⋓</mo>. (Unicode U+22D3, ⋓).
When you say \doublehyphendemerits=92, then TeX will use 92 as additional demerits for a line that ends with a discretionary break and is preceded by an another line with a discretionary break. Unused by Tralics. (See scanint for details of argument scanning).
Distance between two vertical rules in a table; unused by Tralics.
The \downarrow command is valid only in math mode. It generates an arrow that goes down: <mo>↓</mo> (Unicode U+2193, ↓) See description of the \leftarrow command.
The \Downarrow command is valid only in math mode. It generates a double stroke arrow that goes down: <mo>⇓</mo> (Unicode U+21D3, ⇓). See description of the \leftarrow command.
The \downdownarrows command is valid only in math mode. It generates <mo>⇊</mo> (Unicode U+21CA, ⇊)
The \downharpoonleft command is valid only in math mode. It generates <mo>⇃</mo> (Unicode U+21C3, ⇃)
The \downharpoonright command is valid only in math mode. It generates <mo>⇂</mo> (Unicode U+21C2, ⇂)
A command like \dp0=2\dp1 says to replace the depth of the box number zero by twice the depth of box number one. See scanint for how integers are read (here the integer is zero, it should be a number between 0 and 255). See scandimen for how dimensions are read (here 2\dp1 is the dimension).
Tralics does not use nor remember box dimensions. In the example above 2\dp1 evaluates to 0pt, and modifying \dp0 does not modify the box.
The \drawline takes an optional argument [stretch] and N (at least two) coordinates of the form (dx,dy). It connects the given points by drawing a line between each pair of coordinates using line segments of whatever is best in the fount.
No example available. No translation available. Can be used only in a picture environment.
The \dump command outputs a format file that can be loaded at comparatively high speed to restore the current status. Not yet implemented in Tralics.
back to home page
© INRIA 2003, 2004, 2006
Last modified $Date: 2015/11/27 17:06:16 $