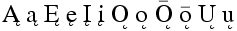
This page contains the description of the following commands
\k,
\kappa,
\ker,
\kern,
keyval,
and environments
keywords.
The \k command generates an ogonek accent. The translation of
\k A \k a \k E \k e \k I \k i \k O \k o \k{\=O} \k{\=o} \k U \k u
is
Ą ą Ę ę Į į Ǫ ǫ Ǭ ǭ Ų ų
Corresponding HTML characters:
Ą ą Ę ę Į į Ǫ ǫ Ǭ
ǭ Ų ų. Latex Image 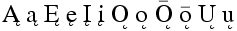
The \kappa command is valid only in math mode. It generates a Greek letter: <mi>κ</mi> (Unicode U+3BA, κ). See description of the \alpha command.
The \ker command is valid only in math mode. Its translation is a math operator of the same name: <mo form='prefix'>ker</mo>. For an example see the \log command.
The command reads a dimension. It should do something with it.
The content of the environment should be a list of comma-separated items. A final dot is removed. Each item is translated. This command was removed in version 2.7, because \keywords{foo,bar} will fail in a very strange manner. The functionality is still there, under the alternate name motscle
We describe here a number of functions defined by the keyval or xkeyval package. The idea is that you can write code of the form \foo{u=1,v=2,w}. The command can execute the action associated to the different keys; this means that the actions have to be registered somewhere. For instance the action of u is in \KV@fam@u. You can chose the family name (fam in the example); the graphicx package uses Gin. The first line in the example defines the action of key u in family fam. The second line defines the action of w, in this case you can omit the value, the default value is in brackets. The xkeyval package allows you to change the prefix. The lines that follow explain which command is defined; note that if a field is empty, the @ separator is omitted.
\define@key{fam}{u}{\typeout{In u, value=#1}}
\define@key{fam}{w}[None]{\typeout{In w, value=#1}}
\define@key[my]{fam}{keyA}[]{} % \my@fam@keyA
\define@key[]{xx}{keyA}{} % \xx@keyA
\define@key[my]{}{keyA}{} % \my@keyA
The command \define@cmdkey defines a key that saves the value in a command, and may perform some additional action. We give here two examples, first with a default prefix, then with MP@. In each case, the effect is the same as the two lines that follow. The default value (x or y) is optional, if omitted the default command is not created.
\define@cmdkey[xKV]{fam}{keyA}[x]{code #1}
%\def\xKV@fam@keyA#1{\def \cmdxKV@fam@keyA {#1}code #1}
%\def\xKV@fam@keyA@default{\xKV@fam@keyA {x}}
\define@cmdkey[xKV]{fam}[MP@]{keyB}[y]{code #1}
%\def\xKV@fam@keyB#1{\def \MP@keyB {#1}code #1}
%\def\xKV@fam@keyB@default{\xKV@fam@keyB {y}}
You can use \define@cmdkeys. This defines a sequence of keys that saves the value; there is no additional action, but the syntax is otherwise the same (all three arguments in brackets are optional).
\define@cmdkeys[xKV]{fam}[MP@]{keyD,keyE}[z]
%\def\xKV@fam@keyD#1{\def \MP@keyD {#1}}
%\def\xKV@fam@keyE#1{\def \MP@keyE {#1}}
%\def\xKV@fam@keyD@default{\xKV@fam@keyD {z}}
%\def\xKV@fam@keyE@default{\xKV@fam@keyE {z}}
You can use \define@choicekey. This defines a choice key. The syntax is the following: the first three arguments define the key. Then comes an optional argument formed of zero, one or two arguments, followed by the list of allowed values, followed by the optional default value followed by the code.
\define@choicekey*[KV]{fam}{keyC}[\val\nr]{a,b}[w]{#1}
%\def\KV@fam@keyC#1{\XKV@cc*[\val \nr ]{#1}{a,b}{#1}}
%\def\foo{\KV@fam@keyC {w}}\isfoo\KV@fam@keyC@default
\define@choicekey*+[KV]{fam}{keyC}[\val\nr]{a,b}{#1}{=#1}
%\def\KV@fam@keyC#1{\XKV@cc*+[\val \nr ]{#1}{a,b}{#1}{=#1}}
The magic command is \XKV@cc. It takes four or five arguments, bin (optional), value (the value of the key), allowed (a comma separated list of tokens), code, and maybe badcode; there are two prefixes, plus and star, the plus prefix says how many arguments are read. If the star prefix is used, then the argument and allowed values are converted to lower case letter. If the key value is not in the list, an error is signaled, unless the plus prefix is used, case where badcode is executed. Otherwise code is executed. If the bin is not empty, it should contain one or two definable commands; the value of the key is stored in the first command (possibly after conversion into lower case); its index is stored in the second command if possible. Said otherwise, if the key value is a in the example above then \nr will hold 0, if the key value is b, it will hold 1.
You can use \define@boolkey. This is like a choice key, with two choices, true and false. The star prefix is implied: a lower case version of the key is always used. If the code below, you can see the \csname command. It starts with some name (here \KV@fam@shadow, but is \my@frame for the example on the last like). Call this foo; the boolean \iffoo is constructed. The \csname sets the boolean, by calling \footrue or \foofalse, the user defined code can use it. The first line is the same as the two other ones.
\define@boolkey+{fam}{shadow}{B#1}{C#1}
%\def\KV@fam@shadow #1{\XKV@cc*+[\XKV@resa ]{#1}{true,false}
% {\csname KV@fam@shadow\XKV@resa \endcsname B#1}{C#1}}
%% \define@boolkey{fam}[my@]{frame}{A#1}
You can use \define@boolkeys. It defines more than one key. The plus prefix is forbidden and no code be given: the effect of setting the key is just to set the boolean. In the example that follows, no error should be signaled.
\define@boolkey{fam}{A}{\xdef\foo{\ifKV@fam@A Atrue\else Afalse\fi}}
\define@boolkeys{fam}{B,C}
\def\Test{Atrue}
\setkeys{fam}{A=true,B=false,C=True}
\ifx\foo\Test \ifKV@fam@B\else \ifKV@fam@C \let\bad\relax\fi\fi\fi
\bad
It is possible to disable a key via \disable@keys; the example below will disable the keys keya, keyb and keyc in the family fam (with prefix my); it is an error to disable an undefined key; otherwise this redefines the key to produced a warning when used. It is possible to check via \key@ifundefined that a key exists in a list of families. The next example should print `key defined' if the key is defined in one of the families, and `key undefined' otherwise. The command \XKV@tfam holds the last family checked; this is the first family in which the key is defined in case of success, the last element of the family list otherwise; in the special case where the family list is empty, the key is undefined and the macro is empty.
\disable@keys[my]{fam}{keya,keyb,keyc}
\key@ifundefined[my]{familya,familyb}{keya}
{\typeout{key undefined}}{\typeout{key defined}}
The command \setkeys sets a sequence of keys. Arguments are an optional prefix (default is KV), followed by a list of families and a list of key-value pairs. For each pair, all families are looked at, and the definition of the first family is considered. In the example that follows, the first \setkeys produces aAabBb, and signals an undefined key error for keyd. In the second case, an error is signaled because keyb has no default value, but CV is used as default value for keyc. The third line shows nesting, it gives: `caa and bacb and cb'. We show two more examples where a star is after the command name; it this case no error is signaled if a key is not found in the list; in this case \XKV@rm will contain the list of undefined keys. Finally, we show that the command can have an additional parameter, that is a list of keys to ignore. The command \setrmkeys is like \setkeys but it sets the keys from \XKV@rm. In the example, it is assumed to set keye and keyf in family cc; this will fail, and since the starred version is used, the result is stored back in \XKV@rm. On the second try, we use the same command to set all these keys, with the exception of keyg. Note that \setkeys and \setrmkeys accept a plus option (to be put after the star, if you want both options); this says that if a key is found in more than one family, it should be defined in all families.
\define@key[X]{familya}{keya}{a#1a}
\define@key[X]{familyb}{keyb}{b#1b}
\define@key[X]{familyb}{keyc}[CV]{c#1c}
\define@key[X]{familyc}{keye}{c#1e}
\define@key[X]{familyc}{keyf}{c#1f}
\setkeys[X]{familya,familyb}{keya=A,keyb=B,keyd=D}
\setkeys[X]{familyb}{keyb,keyc}
\setkeys[X]{familyb}{keyc=a\setkeys[X]{familya}{keya=~and b},keyb=~and c}
\setkeys*[X]{familyb}{keyc,keyd,keye}
%\XKV@rm == {keyd,keye}
\setkeys*[X]{familya,familyb}[keya,keyd]{keyc,keyd,keye=1, keyf=2,keyg=3}
%\XKV@rm == {keye=1,keyf=2,keyg=3}
\setrmkeys*[X]{familycc}
\setrmkeys+[X]{familyc}[keyg]
When executing a key macro, six commands are defined; \XKV@prefix contains the prefix, \XKV@fams contains the list of families to search, \XKV@tfam contains the current family, \XKV@header contains the header which is a combination of the prefix and the current family, \XKV@tkey contains the current key name and \XKV@na contains the list of keys that should not be set. For technical reasons, the @ character has category code 11. Example:
\define@key[X]{familya}{keyc}{%
\edef\vars{prefix=\XKV@prefix, fams=\XKV@fams, this fam=\XKV@tfam,
header=\XKV@header,this key=\XKV@tkey, na=\XKV@na}}
\setkeys*[X]{familya,familyb}[keya,keyd]{keyc=x,keyd,keye=1, keyf= 2, keyg=3}
\show\vars
\vars=macro: ->prefix=X@, fams=familya,familyb,
this fam=familya, header=X@familya@,this key=keyc, na=keya,keyd.
The package provides a mechanism to save the value of a key in variable. In the example below, we show the name of the variable; remember that the prefix my is optional, default value is KV. The difference between \savevalue and \gsavevalue is that the latter saves the value globally.
{
\setkeys[my]{familya}{\savevalue{keya}=test1}
% \XKV@my@familya@keya@value is test1
\setkeys[my]{familya}{\gsavevalue{keya}=test2}
}
% \XKV@my@familya@keya@value is test2
The six functions described now take an optional prefix as argument, and a family, and optionally a key list. In the example, they work on the macro \XKV@my@familya@save; if the command starts with the letter g, the macro is globally modified, otherwise locally. This macro contains the list of the keys that should be automatically saved; this means that \savemacro is implicitly added; after execution of the first line the two lines that follow are identical; in the case of keyc, \gsavemacro is used instead. Line four has as effect to add keyb to the macro, as well as keyc (the old value of keyc with the global flag is discarded). The command \savekeys adds the lists of keys to the macro (unless already present), the command \delsavekeys removes the keys when present, and \unsavekeys clears the macro.
\savekeys[my]{familya}{keya,\global{keyc}}
%\setkeys[my]{familya}{\savevalue{keya}=test5}
%\setkeys[my]{familya}{keya=test5}
\gsavekeys[my]{familya}{keyb,keyc}
\delsavekeys[my]{familya}{keyb}
\gdelsavekeys[my]{familya}{keyw}
\unsavekeys[my]{familya}
\gunsavekeys[my]{familya}
You can use a saved value by using the macro that holds the value; a simpler method consists in using \usevalue; this works only if the family is the same and the command is not hidden in braces. In the example that follows, the value of keyc in familya is xyz. We give then an example where the default value of a keys uses a saved value.
\setkeys[my]{familya}{\savevalue{keya}=y}
\setkeys[my]{familya}{\savevalue{keyb}=\usevalue{keya}}
\setkeys[my]{familya}{keyc=a\usevalue{keyb}z}
\define@key{fam}{keya}{keya: #1}
\define@key{fam}{keyb}[\usevalue{keya}Q]{keyb: #1}
\define@key{fam}{keyc}[\usevalue{keyb}R]{keyc: #1}
\setkeys{fam}{\savevalue{keya}=test}
\setkeys{fam}{\savevalue{keyb}}
\setkeys{fam}{keyc}
The command \presetkeys works the same as \savekeys with two exceptions. It takes two key lists instead of one, and these lists may contain key=value pairs. In the example the two macros \XKV@pre@fama@preseth and \XKV@pre@fama@presett are modified.
\presetkeys[pre]{fama}{keya, keyb=c}{Keya, Keyb=c, \savevalue{Keyc}}
\gpresetkeys[pre]{fama}{keya=1}{Keya=2}
\delpresetkeys[pre]{fama}{keya}{Keya}
\gdelpresetkeys[pre]{fama}{keya}{Keya}
\unpresetkeys[pre]{fama}
\gunpresetkeys[pre]{fama}
This is an example of presetting keys. We tell the system to set keya before the user keys, and keyb after that; these settings are skipped if the user specifies a key. The order of evaluation is important in this example because keyb uses a value saved by keya.
\define@key[my]{familya}{keya}{\typeout{keya: #1}}
\define@key[my]{familya}{keyb}{\typeout{keyb: #1}}
\define@key[my]{familya}{keyc}{\typeout{keyc: #1}}
\savekeys[my]{familya}{keya}
\presetkeys[my]{familya}{keya=blue}{keyb=\usevalue{keya}}
\setkeys[my]{familya}{keya=red}
\setkeys[my]{familya}{keyc=green}
The commands shown on the first three lines below can appear in a package or class file. When you declare an option with \DeclareOptionX (in package or class foo), you really declare a key in family foo.cls or foo.sty; the example shows the strange syntax to use if you want the family to be foo.bar. If no default value is given, an empty one is provided. The command \ExecuteOptionsX behaves like \setkeys (the same algorithm is used to set get the family). This command is provided by the package writer in order to initialise the variables in the package; as a consequence, there are no presets, no list of keys to ignore, and no error should happen. The command \ProcessOptionsX sets the keys passed as arguments to the package or class. In the current version of Tralics a list of strings (the keys) is maintained for use with commands without extension X. Mixing these two methods is not provided in version 2.11.5. This means that \ProcessOptionsX has no access to global class options, and if used in a class, does not pass these options to packages. Moreover an optional star is ignored.
\DeclareOptionX{opA}[def-val]{\def\opA{#1}}
\ExecuteOptionsX{keya,keyb=1}
\ProcessOptionsX \relax
%\DeclareOptionX[my]<foo.bar>{landscape}{\landscapetrue}
%\usepackage[opA,opB=C,opC=\foo,opE]{testkeyval}
back to home page
© INRIA 2003-2005, 2006
Last modified $Date: 2015/08/04 15:54:02 $