 See description of the
\ldots command.
See description of the
\ldots command.
This page contains the description of \@ne, \nabla, \@namedef, \@nameuse, \natcite, \natural, \ncong, \nearrow, \ne, \NeedsTeXFormat, \neg, \neq, \newblock, \newboolean, \newbox, \newcolumntype, \newcommand, \newcount, \newcounter, \newdimen, \newenvironment, \newfont, \newif, \newindex, \@newindex, \newlength, \newlanguage, \newline, \newlinechar, \newsmukip, \newpage, \newread, \newsavebox, \newskip, \newtoks, \newtheorem, \newwrite, \nexists, \ng, \ngeq, \ngtr, \NG, \ni, \@nil, \niplus, \@nnil, \nleftarrow, \nLeftarrow, \nLeftrightarrow, \nleftrightarrow, \nleq, \nless, \nmid, \no, \No, \noalign, \noboundary, \nobreak, \nobreakspace, \nocentering, \nocite, \node, \nodebox, \nodecircle, \nodeconnect, \nodecurve, \nodeoval, \nodepoint, \nodetriangle, \noexpand, \nonfrenchspacing, \noindent, \nointerlineskip, \nolimits, \nolinebreak, \@nomathml, \@nomathswi, \@nomathswii, \nonscript, \nonstopmode, \nonumber, \noopsort, \nopagebreak, \normalbaselines, \normalbaselineskip, \normalcolor, \normalfont, \normallineskip, \normallineskiplimit, \normalmarginpar, \normalsize, \not, \NOT, \notag, \notin, \@notprerr, \notrivialmath, \nparallel, \nprec, \nRightarrow, \nrightarrow, \nsim, \nsubseteq, \nsucc, \nsupseteq, \ntriangleleft, \ntrianglelefteq, \ntrianglelefteqslant, \ntriangleright, \ntrianglerighteq, \ntrianglerighteqslant, \nu, \null, \nulldelimiterspace, \nullfont, \number, \numberedverbatim, \numberwithin, \numero, \Numero, \numexpr, \nvdash, \nvDash, \nVdash, \nVDash, \nwarrow.
The \nabla command is valid only in math mode. It generates a miscellaneous symbol: <mi>∇</mi> (Unicode U+2207, ∇). See description of the \ldots command.
Instead of \expandafter\def\csname xxx\endcsname ... you can say \@namedef{xxx}.... The result is the same.
Instead of \csname xxx\endcsname you can say \@nameuse{xxx}. For instance, if you have two counters A and B, and you want that A prints in the same way as B, more precisely, you want \theA to call \theB, you say \Test{A}{B}, after the following definition: \def\Test#1#2{\global \@namedef {the#1}{\@nameuse {the#2}}}.
The \natural command is valid in math mode and text mode. It generates a miscellaneous symbol: <mo>♮</mo> (Unicode U+266E, ♮). See description of the \qquad and \ldots commands.
The \ncong command is valid only in math mode. It generates: <mo>&2247;</mo>, ≇.
The \ne command is valid only in math mode. It generates a relation symbol: <mo>≠</mo> (Unicode U+2260, ≠). See description of the \le command.
The \nearrow command is valid only in math mode. It generates an arrow that points North-East: <mo>↗</mo> (Unicode U+2197, ↗). See description of the \leftarrow command.
A typical class file contains a declaration like \NeedsTeXFormat{LaTeX2e}[1995/12/01]. This is ignored by Tralics.
The \neg command is valid only in math mode.
It generates a miscellaneous symbol
(character ¬).
 See description of the
\ldots command.
See description of the
\ldots command.
The \neq command is valid only in math mode. It is the same as \ne. It generates a relation symbol: <mo>≠</mo> (Unicode U+2260, ≠). See description of the \le command.
This command expands to \hskip .11em plus.33em minus.07em.
You can say \newboolean{foo}, this is the same
as \newif\iffoo. However, an error is signaled
if \iffoo already
exists. The control sequence \iffoo
is created by \csname, nasty
errors may occur. The boolean value of foo can be changed by
setboolean{foo} (rather than by \footrue
or \foofalse). It can be tested via \boolean.
 (see description of \ifthenelse)
(also see \newif) for some
details).
(see description of \ifthenelse)
(also see \newif) for some
details).
Example (translation is oka okb)
{ %The command \bad is not executed here
\def\double#1{#1#1}
\newboolean{f\double o}
\def\swap{\setboolean{f\double o}{\iffoo fals \else TRU\fi e}}
\ifthenelse{\boolean{foo}}{\bad}{oka}
\swap
\ifthenelse{\boolean{foo}}{okb}{\bad}
}
The \newbox command is similar in principle to
\newcount.
After \newbox\foo, the \foo commands
refers to some box, and each call to \newbox produces a
reference to a different box. You say \setbox\foo = \hbox{...}
if you want to put something in the box, \box\foo or
\copy\foo if you want to use the box or its copy.
Note: \foo is, in reality, a reference to a character.
(Lamport calls it a bin
).
The \newcolumntype command can be used to define a new column
type (in addition to flush left, flush right and center).
 See documentation
on arrays.
See documentation
on arrays.
The LaTeX way of defining commands is via \newcommand. Here are some examples
\newcommand*\NCA{nca}
\newcommand{\NCB}[0]{ncb}
\newcommand{\NCC}[2]{ncc#1#2}
\newcommand{\NCD}[2][x]{ncd#1#2}
\NCA and \NCB and \NCC{arg1}{arg2} and
\NCD[arg1]{arg2} and \NCD{arg2}
The argument of \newcommand should be a single token (\cmd25 is wrong), a command name (or an active character) that is undefined. It is followed by the number of arguments (in brackets, default is zero, only explicit digits are allowed), followed by an optional argument in brackets, followed by a command body. In the body, #1 refers to the first argument, #2 to the second, etc (you cannot use #7 if the command does not take at least seven arguments).
In the case of a command like \NCD, the number of arguments should be at least one. When you say \NCC{y}, then y is the second argument (and the first argument takes its default value, here x). When you say \NCD[1]{2}, the first argument is 1, the second argument is 2. The commands are \long (they accept \par in their arguments), unless \newcommand* is used ( You can put an optional * after \newcommand, (it means non-\long in LaTeX).
This command allocates a new counter register and defines a macro that references it.
There are N=256 count registers, indexed by a number between 0 and N-1, for instance \count0, or \count23. (In current versions of Tralics, N is 1024). It is sometimes wise to give a symbolic name to a counter. For instance, \countdef\foo 25 makes \foo a reference to \count25. On the other hand, it is more efficient to say \foo than \count25, (because it avoids a call to scanint) and \foo3 is not the same as \count253.
There is a mechanism that makes sure that a register is not used
more than once: the \newcount command uses
a different number each time, first 20, then 21, then 22, etc.
Numbers less than 10 are not allocated. Numbers between 10 and 19 are used by
the new-something mechanism.
When you say
\newcount\foo, a counter is allocated, and \foo
is made a reference to it. Then \foo=3 puts 3 in the counter,
\advance\foo by 1 increments the counter, and
\the\foo typesets the counter.
Allocation is always global.
 See \loop for an example.
See \loop for an example.
The \newcounter command is similar in principle to \newcount. However, LaTeX adds additional features. When you say \newcounter\foo, a number is allocated, say 25, and the command \c@foo is made equivalent to \count25. See for instance description of counters. The expression \value{foo} expands to \c@foo, hence to \count25. This means that \value{foo}=12 is one way to set the value to 12, but you should say \setcounter{foo}{12}. This sets the value to 12, globally. You can also say \addtocounter{foo}{25}, if you want to add (globally) 25 to the value of the counter.
You can say \number\value{foo} if you want to typeset the number, and even \the\value{foo}. If fact, you say \arabic{foo} if you want an arabic version (you can use \roman, \alph etc). You say \thefoo when you want to typeset the counter foo and what is related (default value is arabic, but you can say \renewcommand \thefoo {\roman{foo}}). You can say: \renewcommand \thesection {\thechapter .\arabic{section}}. Then \thesection typesets \thechapter, a dot, and the section counter as an arabic number.
When you say \newcounter {section}[chapter], this modifies a property of the chapter counter (in fact the \cl@chapter command), so that, whenever it is incremented by \stepcounter, the section counter is reset to zero. Example
{
\newcounter{toto}
\newcounter{titi}[toto]
\newcounter{tata}[titi]
\newcounter{tutu}[toto]
\setcounter{toto}{10}
\setcounter{titi}{20}
\setcounter{tata}{30}
\setcounter{tutu}{40}
\expandafter\show\value{toto}\expandafter\showthe\value{toto}
\expandafter\show\value{titi}\expandafter\showthe\value{titi}
\expandafter\show\value{tata}\expandafter\showthe\value{tata}
\expandafter\show\value{tutu}\expandafter\showthe\value{tutu}
\stepcounter{toto} % kills titi, tutu
\stepcounter{tata}\thetata=31,
\stepcounter{titi}\thetata=0 % titi=1
\stepcounter{tutu}
\thetoto\thetiti\thetata\thetutu=11101
\makeatletter
\show\cl@toto
\show\cl@titi
\show\cl@tata
\show\cl@tutu
}%
Translation is: 31=31, 0=0 11101=11101. Tralics prints the following. Note that \c@toto is a pointer into an internal table that contains catcodes, lccodes, etc. [In old version of Tralics, \show\c@toto gave \countref1536, because the counter is at position 1536 if the integer part of eqtb table].
\c@toto=\count26.
\show: 10
\c@titi=\count27.
\show: 20
\c@tata=\count28.
\show: 30
\c@tutu=\count29.
\show: 40
\cl@toto=macro: ->\@elt {titi}\@elt {tutu}.
\cl@titi=macro: ->\@elt {tata}.
\cl@tata=macro: ->.
\cl@tutu=macro: ->.
The \newdimen command is similar in principle to
\newcount.
When you say \newdimen\foo, then \foo is a
reference to one of the N dimension registers. You can use
\foo in the same way as \dimen0. For instance
\foo=25pt will set the dimension to 25pt.
It is the same as \setlength{\foo}{25pt}. You can say
\advance\foo by 3pt if you want to increase the value,
or you can say \addtolength{\foo}{3pt}.
In TeX N=256, in the current version of Tralics it is 1024.
An environment, like foo is defined by two commands \foo and \endfoo. It is defined by the \newenvironment command, that takes as argument a name (Tralics accepts only characters); the command associated to this name should not be already defined.
For instance, \newenvironment{foo} {xxx} {yyy} is like \newcommand{\foo}{xxx}, \def\endfoo{yyy}. Said otherwise, the \foo command can take some arguments, it can take an optional argument, but \endfoo takes no argument (in the case of DDD, we put the argument in an auxiliary command, that will be used at the end of the environment). Example
\newenvironment{AAA}{1\begin{BBB}5}{8\end{BBB}c}
\newenvironment{BBB}{2\begin{CCC}4}{9\end{CCC}b}
\newenvironment{CCC}{3}{a}
\newenvironment{DDD}[2]{#2#1\def\foo{#1}}{\foo}
\newenvironment{EEE}[2][e]{#2#1\def\foo{#1}}{\foo}
%latex code translation
\begin{AAA}67\end{AAA} 123456789abc
\begin{DDD}678\end{DDD} 7686
\begin{EEE}[6]78\end{EEE} 7686
\begin{EEE}78\end{EEE} 7e8e
This command is a wrapper around \font in that the expansion of \newfont\foo{cmt at 12pt} is \font\foo=cmt at 12pt\relax.
After \newif\iffoo, the two commands \footrue
and \foofalse are defined: the result of these commands
is to change the meaning of \iffoo to \iftrue and
\iffalse respectively. Moreover, \iffoo
is let equal to \iffalse initially.
 See \loop for an example. Note that Tralics
wants a name with at least 3 characters.
See \loop for an example. Note that Tralics
wants a name with at least 3 characters.
This is how the macro is defined in plain TeX (why does the TeXbook mention `\edef' ?)
\outer\def\newif#1{\count@\escapechar \escapechar\m@ne
\expandafter\expandafter\expandafter
\def\@if#1{true}{\let#1=\iftrue}%
\expandafter\expandafter\expandafter
\def\@if#1{false}{\let#1=\iffalse}%
\@if#1{false}\escapechar\count@} % the condition starts out false
\def\@if#1#2{\csname\expandafter\if@\string#1#2\endcsname}
{\uccode`1=`i \uccode`2=`f \uppercase{\gdef\if@12{}}} % `if' is required
This is how the macro is defined in LaTeX:
\def\newif#1{%
\count@\escapechar \escapechar\m@ne
\let#1\iffalse
\@if#1\iftrue
\@if#1\iffalse
\escapechar\count@}
\def\@if#1#2{%
\expandafter\def\csname\expandafter\@gobbletwo\string#1%
\expandafter\@gobbletwo\string#2\endcsname
{\let#1#2}}
These commands allow you to use more than one index, see \index.
The \newlanguage command is similar in principle to \newcount, but it allocates a language number (starting with 11). This is currently unused by Tralics that knows only English, French and German with numbers 0, 1 and 2.
The \newlength command (and its synonym \newskip) is similar in principle to \newcount, but it allocates a skip register.
When you say \newlength\foo, then \foo is a
reference to one of the N skip registers. You can use
\foo in the same way as \skip0. For instance
\foo=25pt plus 2pt will set the dimension to 25pt plus 2pt.
It is the same as \setlength{\foo}{25pt plus 2pt}. You can say
\advance\foo by 3pt plus 4pt if you want to increase the value,
or you can say \addtolength{\foo}{3pt plus 4pt}.
Note: the commands \setlength and \addtolength
use as first argument a dimen register or a skip register (more generally,
anything that can be preceded by \advance\, for instance
\parindent), the second argument will be automatically
converted (by adding zero shrink and stretch, or by ignoring the shrink and
stretch components).
 (see also \newcount)
(see also \newcount)
In TeX N=256, in the current version of Tralics it is 1024.
The \newline command is like \\, without optional argument. It does not work inside an array. See \\.
The \newlinechar command can be used to change the value of
the character that TeX uses for a new line (for instabce in \write)
Not implemented in Tralics.
 (See scanint for details of argument scanning).
(See scanint for details of argument scanning).
The \newmuskip command is similar in principle to \newcount, but it allocates a muskip register.
Translation of \newpage is <newpage/>.
The \newread command is similar in principle to \newcount, but it allocates an input stream (first number allocated is 1, last one is 15).
The \newsavebox command is similar to \newbox (in the current version, Tralics does not check that the command is undefined).
The \newskip command is similar in principle to \newcount, but it allocates a skip register. It is the same as \newlength.
You can say \newtheorem {X}{Y} or \newtheorem {X}[Z}{Y} or \newtheorem {X}{Y}[T}. This defines an environment X, labeled Y. In the second case, it uses the counter Z, otherwise it uses X as counter. In the last case, the counter is reset whenever T changes and the value of T is prepended to the value of X.
There is a command \theoremstyle that takes an argument, and remembers it; each theorem can see the value that was active at the definition. In the first case shown below, and in the preview, this value is ignored.
There is a command \theorembodyfont that takes an argument, and remembers it; each theorem uses this value as font for the body.
There is a command \theoremheaderfont that takes an argument, and remembers it; each theorem uses this value as font for the body. For some strange reason, this quantity is global (should be used only once). Example.
\theorembodyfont{\sl}
\theoremstyle{break}
\newtheorem{Cor}{Corollary}
\theoremstyle{plain}
\setcounter{section}{17}
\newtheorem{Exa}{Example}[section]
{\theorembodyfont{\rmfamily}\newtheorem{Rem}{Remark}}
\theoremstyle{marginbreak}
\newtheorem{Lem}[Cor]{lemma}
\theoremstyle{change}
\theorembodyfont{\small\itshape} \newtheorem{Def}[Cor]{Definition}
\theoremheaderfont{\scshape}
\def\Lenv#1{\texttt{#1}}
\begin{Cor}
This is a sentence typeset in the theorem environment \Lenv{Cor}.
\end{Cor}
\begin{Exa}
This is a sentence typeset in the theorem environment \Lenv{Exa}.
\end{Exa}
\begin{Rem}
This is a sentence typeset in the theorem environment \Lenv{Rem}.
\end{Rem}
\begin{Lem}[Ben User]
This is a sentence typeset in the theorem environment \Lenv{Lem}.
\end{Lem}
\begin{Def}[Very Impressive definition]
This is a sentence typeset in the theorem environment \Lenv{Def}.
\end{Def}
The translation is the following.
<p id-text='1' id='uid1'> <hi rend='sc'>Corollary 1 </hi> <hi rend='slanted'>This is a sentence typeset in the theorem environment </hi> <hi rend='slanted'><hi rend='tt'>Cor</hi></hi><hi rend='slanted'>.</hi> </p> <p id-text='17.1' id='uid2'> <hi rend='sc'>Example 17.1 </hi> <hi rend='slanted'>This is a sentence typeset in the theorem environment </hi> <hi rend='slanted'><hi rend='tt'>Exa</hi></hi> <hi rend='slanted'>.</hi> </p> <p id-text='1' id='uid3'> <hi rend='sc'>Remark 1 </hi> This is a sentence typeset in the theorem environment <hi rend='tt'>Rem</hi>. </p> <p id-text='2' id='uid4'> <hi rend='sc'>lemma 2 (Ben User) </hi> <hi rend='slanted'> This is a sentence typeset in the theorem environment </hi> <hi rend='slanted'><hi rend='tt'>Lem</hi></hi> <hi rend='slanted'>.</hi> </p> <p id-text='3' id='uid5'> <hi rend='sc'>Definition 3 (Very Impressive definition) </hi> <hi rend='small1'></hi> <hi rend='small1'> <hi rend='it'> theorem} This is a sentence typeset in the theorem environment </hi> </hi> <hi rend='small1'><hi rend='it'><hi rend='tt'>Def</hi></hi></hi> <hi rend='small1'><hi rend='it'>.</hi></hi> </p>
The preview is the following

Note that the theorem counter is incremented via a call to \refstepcounter, in fact to \stepcounter plus the internal code that defines a label. In this case, the label is put on an anonymous XML element, then copied to the <p> element. If the configuration file contains xml_xtheorem_name = "dummy", then the name will be dummy, and the result of the translation will be
<dummy id-text='1' id='uid3'> <p> <hi Rend='sc'>Remark 1 </hi> This is a sentence typeset in the theorem environment <hi Rend='tt'>Rem</hi>. </p> </dummy>
If the configuration file contains xml_theorem_name = "theorem", then the name will be theorem, and the translation is a bit different, as you can see.
<theorem style='break' type='Cor' id-text='1' id='uid1'> <head>Corollary</head> <p>This is a sentence typeset in the theorem environment <hi Rend='tt'>Cor</hi>. </p> </theorem> <theorem style='plain' type='Exa' id-text='17.1' id='uid2'> <head>Example</head> <p>This is a sentence typeset in the theorem environment <hi Rend='tt'>Exa</hi>. </p> </theorem> <theorem style='plain' type='Rem' id-text='1' id='uid3'> <head>Remark</head> <p>This is a sentence typeset in the theorem environment <hi Rend='tt'>Rem</hi>. </p> </theorem> <theorem style='marginbreak' type='Lem' id-text='2' id='uid4'> <head>lemma</head> <alt_head>Ben User</alt_head> <p>This is a sentence typeset in the theorem environment <hi Rend='tt'>Lem</hi>. </p> </theorem> <theorem style='change' type='Def' id-text='3' id='uid5'> <head>Definition</head> <alt_head>Very Impressive definition</alt_head> <p>This is a sentence typeset in the theorem environment <hi Rend='tt'>Def</hi>. </p> </theorem>
The \newtoks command is similar in principle to \newcount, but it allocates a token register. Assuming that the first allocated register is 11, the following code makes \foo equivalent to \Bar. The translation is `123 456'.
\toksdef\foo 11
\newtoks\Bar
\foo={123 456} \the\Bar
The \newread command is similar in principle to \newcount, but it allocates a output stream (first number allocated is 1, last one is 15).
The \nexists command is valid only in math mode. It generates: <mo>∄</mo> (Unicode U+2204, ∄).
This translates to ŋ or (Unicode U+14B, ŋ). For more info see the extended latin characters.
This translates to Ŋ (Unicode U+14A, Ŋ). For more info see the extended latin characters.
The \ngeq command is valid only in math mode. It generates: <mo>≱</mo> (Unicode U+2271, ≱).
The \ngtr command is valid only in math mode. It generates: <mo>≯</mo> (Unicode U+226F, ≯).
The \ni command is valid only in math mode. It generates: <mo>∋</mo> (Unicode U+220B, ∋).
The \niplus command is valid only in math mode. It generates: <mo>&niplus;</mo> (Unicode U+2A2E, ⨮).
The \nleftarrow command is valid only in math mode. It generates: <mo>↚</mo> (Unicode U+219A, ↚).
The \nLeftarrow command is valid only in math mode. It generates <mo>⇍</mo> (Unicode U+21CD, ⇍).
The \nleftrightarrow command is valid only in math mode. It generates: <mo>↮</mo> (Unicode U+21AE, ↮).
The \nLeftrightarrow command is valid only in math mode. It generates <mo>⇎</mo> (Unicode U+21CE, ⇎).
The \nleq command is valid only in math mode. It generates: <mo>≰</mo> (Unicode U+2270, ≰).
The \nless command is valid only in math mode. It generates: <mo>≮</mo> (Unicode U+226E, ≮).
The \nmid command is valid only in math mode. It generates: <mo>∤</mo> (Unicode U+2224, ∤).
The \noalign command can be used to insert material between rows in a table. For instance, in LaTeX, the \hline command is defined to be \noalign{\hrule height \arrayrulewidth}, with a special hack that allows double rules.
In Tralics, the only inter-row material allowed is a single \hline. The \noalign command is not yet implemented.
The \noboundary command inhibits adding an invisible boundary character. This is used by TeX when computing ligatures and kerns. These quantities depend on the current font. Since Tralics does not read font information, the \noboundary is useless. It fact, the command provokes an error.
This commands is currently ignored.
The \nobreakspace command is identical to ~ (tilde), but cannot be used in math mode. It generates a non-break space or  . For more info see the latin supplement characters.
Switches to the default mode, that is not centering, nor flush left, not flush right, nor quotation. (see also \centering)
This commands behaves like \cite, but translation is empty (see also \cite).
You say \node{x}{y} for creating a node named x with value y in a tree. See \abarnodeconnect for syntax and example.
You say \nodebox{x} if you want to put a box around node x. See \abarnodeconnect for syntax and example.
You say \nodebox[3pt]{x} if you want to put a circle around node x. See \abarnodeconnect for syntax and example.
You say \nodeconnect[t]{x}[b]{y} if you want to connect top of node x to bottom of node y. See \abarnodeconnect for syntax and example.
You say \nodeconnect[t]{x}[b]{y}{2pt}[3pt] if you want to connect top of node x to bottom of node y, with a curve specified by 2pt and 3pt. See \abarnodeconnect for syntax and example.
You say \nodeoval{x} if you want to put an oval around node x. See \abarnodeconnect for syntax and example.
You say \nodepoint{x}[4pt][5pt] if you want to create a node named x at the current position, with size 4pt and 5pt. See \abarnodeconnect for syntax and example.
You say \nodetriangle{x}{y} if you want to connect nodes x and y by a triangle. See \abarnodeconnect for syntax and example.
The \noexpand command inhibits expansion of the token
that follows. In the example that follows, you will see \jobname =texput
,
but the translation is texput=texput. In the
test that follows, the tidle character is not expanded, so category
code 13 is compared to what follows; this is the first token in the
expansion of \jn (since this is the first character
of \jobname, the category code is 12, unless the file
starts with a space). In the test that follows, we compare an
unexpanded active character W; it has the same category code as
unexpanded tilde, it has the same value as \foo.
The token that follows \noexpand is considered to
be \relax when it is expandable (in particular, when it
is undefined). The line marked bad
gives three errors: since
unexpanded \foo is illegal in a control sequence name, this
aborts the construction of the name, so you get an undefined error
followed by an extra \endcsname.
The syntax rules for \hbox
and \uppercase allow \relax before the open
brace, so that last line is valid. The resulting box is empty.
\edef \jn {\noexpand \jobname=\jobname} \show\jn \jn
\ifcat\noexpand~\jn \bad \fi \ifcat=\jn \else \bad \fi
{\let\foo=W \catcode`W=13
\ifcat\noexpandW\noexpand~\else \bad \fi
\if\noexpandW\foo\else \bad \fi
\if\noexpandW\noexpand\foo\else \bad \fi
}
\let\foo\undefined
\csname\noexpand\foo\endcsname %bad
\hbox to 2cm \noexpand\foo {\noexpand\foo \uppercase\noexpand\foo{}}
In the example that follows, the non-expanded \foo finishes parsing of the integer; it is expanded again. In the line that follows, expansion is inhibited while scanning the to keyword. Hence \foo is expanded again and is considered as an opening brace. In the line that follows, the second \noexpand is eaten by scanning the spread keyword. So it requires three \noexpand in order to discard \foo. In the two lines that follow, the non-expanded \foo terminates scanning of the number, and becomes part of the unit of measure. Consider the last line: how many \noexpand tokens are needed to effectively suppress expansion (and provoke an error)?. Quite a lot: mote than five in Tralics and 15 in TeX. The syntax of a dimension is quite complicated (see scandimen) and each time an optional thing is tried, one \noexpand is eaten. For instance, one could have em, ex or true. After that Tralics read two characters and compares them with pt, pc, etc, while TeX scan eleven keywords, one after the other.
\def\foo{0} \count0=1\noexpand\foo
\def\foo{\bgroup}\hbox\noexpand\foo x\egroup
\hbox\noexpand\noexpand\foo y\egroup
\hbox\noexpand\noexpand\noexpand\foo{z}
\def\foo{pt} \dimen0=2\noexpand\foo
\def\foo{.5pt} \dimen0=2\noexpand\foo % error
%\def\foo{sp} \dimen0=2\noexpand\noexpand...\foo
This command is ignored by Tralics; in LaTeX it inhibits writing on auxiliary output files.
The \nonfrenchspacing command is ignored. In LaTeX, this modifies the \sfcode value of some punctuation characters to values greater than 1000.
The \noindent command starts a new paragraph.
According to TeX, the only difference between \indent and \noindent is that the first command inserts an empty hbox whose width is \parindent. A new paragraph is started only if TeX is in vertical mode, and the \everypar tokens are inserted in TeX's input. If TeX is in vertical mode and sees a character or something like that (including the first token of the expansion of \leavevmode) it adds an implicit \indent.
In Tralics, the value of \parindent is ignored, as well as the \everypar tokens. Paragraphs are indented by default, so that \noindent adds an attribute, the other command does nothing. If the current text is centered, flushed left or flushed right, no attribute is added. Example
\def\sample{This is some text explaining and showing how text is centered,
flushed left or flushed right or indented or not indented. \Env}
\def\line{\sample\noindent\sample\indent\sample}
\def\Env{Mode is normal}\line
\begin{center}\def\Env{Mode is center}\line\end{center}
\begin{flushleft}\def\Env{Mode is left}\line\end{flushleft}
\begin{flushright}\def\Env{Mode is right}\line\end{flushright}
<p> This is some text explaining and showing how text is centered, flushed left or flushed right or indented or not indented. Mode is normal</p> <p noindent='true'>This is some text explaining and showing how text is centered, flushed left or flushed right or indented or not indented. Mode is normal</p> <p>This is some text explaining and showing how text is centered, flushed left or flushed right or indented or not indented. Mode is normal</p> <p rend='center'>This is some text explaining and showing how text is centered, flushed left or flushed right or indented or not indented. Mode is center</p> <p rend='center'>This is some text explaining and showing how text is centered, flushed left or flushed right or indented or not indented. Mode is center</p> <p rend='center'>This is some text explaining and showing how text is centered, flushed left or flushed right or indented or not indented. Mode is center</p> <p rend='flushed-left'>This is some text explaining and showing how text is centered, flushed left or flushed right or indented or not indented. Mode is left</p> <p rend='flushed-left'>This is some text explaining and showing how text is centered, flushed left or flushed right or indented or not indented. Mode is left</p> <p rend='flushed-left'>This is some text explaining and showing how text is centered, flushed left or flushed right or indented or not indented. Mode is left</p> <p rend='flushed-right'>This is some text explaining and showing how text is centered, flushed left or flushed right or indented or not indented. Mode is right</p> <p rend='flushed-right'>This is some text explaining and showing how text is centered, flushed left or flushed right or indented or not indented. Mode is right</p> <p rend='flushed-right'>This is some text explaining and showing how text is centered, flushed left or flushed right or indented or not indented. Mode is right</p>

The \nointerlineskip command is ignored. In TeX, it sets \prevdepth dimension to a magic value.
The \nolimits command is valid only in math mode.
It describes how indices should be positioned.
In the case of \mathop a\limits ^b, the translation is a
<mover> element containing a and b, rather than
a <msup>. If you forget the \mathop,
an error will be signaled by TeX, but Tralics simply ignores the
command. There are three flags, \limits, \nolimits
and \displaylimits whose meaning is: use always over, use never
over, use over in display mode only. More than one prefix can be given, the
last one has precedence. A command like \lim
has \mathop and \displaylimits flags,
while \sin has \mathop and \nolimits
flags. It happens that the kernel in <mover> can
have a `movablelimits' attribute, case where the effect is the same as
\displaylimits; this may confuse Tralics, in the case
where the attribute is implicit.
 (see also here)
For details see \mathord.
(see also here)
For details see \mathord.
\def\A#1{\mathop a #1_b, \mathop a#1^c, \mathop a#1_b^c}
$\A{} \A\limits \A\nolimits \A\displaylimits $
\[\A{} \A\limits \A\nolimits \A\displaylimits \]
<formula type='inline'>
<math xmlns='http://www.w3.org/1998/Math/MathML'>
<mrow>
<msub><mi>a</mi> <mi>b</mi> </msub> <mo>,</mo>
<msup><mi>a</mi> <mi>c</mi> </msup> <mo>,</mo>
<msubsup><mi>a</mi> <mi>b</mi> <mi>c</mi></msubsup>
<munder><mi>a</mi> <mi>b</mi> </munder> <mo>,</mo>
<mover><mi>a</mi> <mi>c</mi> </mover> <mo>,</mo>
<munderover><mi>a</mi> <mi>b</mi> <mi>c</mi></munderover>
<msub><mi>a</mi> <mi>b</mi> </msub> <mo>,</mo>
<msup><mi>a</mi> <mi>c</mi> </msup> <mo>,</mo>
<msubsup><mi>a</mi> <mi>b</mi> <mi>c</mi> </msubsup>
<msub><mi>a</mi> <mi>b</mi> </msub> <mo>,</mo>
<msup><mi>a</mi> <mi>c</mi> </msup> <mo>,</mo>
<msubsup><mi>a</mi> <mi>b</mi> <mi>c</mi> </msubsup>
</mrow>
</math>
</formula>
<formula type='display'>
<math mode='display' xmlns='http://www.w3.org/1998/Math/MathML'>
<mrow>
<munder><mi>a</mi> <mi>b</mi> </munder> <mo>,</mo>
<mover><mi>a</mi> <mi>c</mi> </mover> <mo>,</mo>
<munderover><mi>a</mi> <mi>b</mi> <mi>c</mi> </munderover>
<munder><mi>a</mi> <mi>b</mi> </munder> <mo>,</mo>
<mover><mi>a</mi> <mi>c</mi> </mover> <mo>,</mo>
<munderover><mi>a</mi> <mi>b</mi> <mi>c</mi> </munderover>
<msub><mi>a</mi> <mi>b</mi> </msub> <mo>,</mo>
<msup><mi>a</mi> <mi>c</mi> </msup> <mo>,</mo>
<msubsup><mi>a</mi> <mi>b</mi> <mi>c</mi> </msubsup>
<munder><mi>a</mi> <mi>b</mi> </munder> <mo>,</mo>
<mover><mi>a</mi> <mi>c</mi> </mover> <mo>,</mo>
<munderover><mi>a</mi> <mi>b</mi> <mi>c</mi> </munderover>
</mrow>
</math>
</formula>
The variable \@nomathml controls translation of mathematical formulas. The default value is zero, and a MathML object is constructed. If the variable is positive, all math-commands translate to themselves; for instance the translation of \int_x^{-\infty} becomes \int_x^-\infty. If the argument is negative, the translation depends on whether the argument is -2 or -3 or some other value. Consider the following input:
\def\myvar{\phi}
$\int_{-\infty}^\myvar f(x) dx=\mathrm{O}\,\left(\frac{1}\myvar\right)$
$x_{\mbox{{\scriptsize{H\,{\sc i}}}}}$
\begin{equation}\text{a}=\hbox{b}=\mbox{c}\end{equation}
This is the translation in case \@nomathml=-2. You can notice that translation of simple objects like \phi is an empty element of the same name, and that braces (even implicit ones, for instance the second argument of the fraction) produces a <arg> element.
<texmath textype='inline' type='inline'>
<int/><subscript><arg>-<infty/></arg></subscript>
<superscript><phi/></superscript>
f(x) dx=<mathrm/><arg>O</arg>
<elt name=','/><left del='('><frac><arg>1</arg><arg><phi/></arg></frac>
<right del=')'>
</texmath>
<texmath textype='inline' type='inline'>
x<subscript>
<arg>
<mbox>
<arg>
<scriptsize/><arg>H<elt name=','/><arg><sc/>i</arg></arg>
</arg>
</mbox>
</arg>
</subscript>
</texmath>
<texmath id-text='1' id='uid1' textype='equation' type='display'>
<text>a</text>=<hbox>b</hbox>=<mbox>c</mbox>
</texmath>
Translation of the same example, with \@nomathml=-1. It is a single XML element, containing the TeX source (after macro-expansion).
<texmath textype='inline' type='inline'>
\int _{-\infty }^\phi f(x) dx=\mathrm {O}\,\left(\frac{1}{\phi }\right)
</texmath>
<texmath textype='inline' type='inline'>
x_{\mbox{{\scriptsize {H\,{\sc i}}}}}</texmath>
<texmath id-text='1' id='uid1' textype='equation' type='display'>
\text{a}=\hbox{b}=\mbox{c}
</texmath>
Translation of the same example, with \@nomathml=-3. The translation is a merge of the cases 0 and -1. More precisely, a <texmath> is created, and inserted in the <formula> after the <math>.
<formula type='inline'>
<math xmlns='http://www.w3.org/1998/Math/MathML'>
<mrow>
<msubsup>
<mo>∫</mo>
<mrow><mo>-</mo><mi>∞</mi></mrow>
<mi>ϕ</mi>
</msubsup>
<mi>f</mi>
<mrow><mo>(</mo><mi>x</mi><mo>)</mo></mrow>
<mi>d</mi><mi>x</mi><mo>=</mo>
<mi mathvariant='normal'>O</mi><mspace width='0.166667em'/>
<mfenced separators='' open='(' close=')'>
<mfrac><mn>1</mn> <mi>ϕ</mi></mfrac>
</mfenced>
</mrow>
</math>
<texmath>
\int _{-\infty }^\phi f(x) dx=\mathrm {O}\,\left(\frac{1}{\phi }\right)
</texmath>
</formula>
<formula type='inline'>
<math xmlns='http://www.w3.org/1998/Math/MathML'>
<msub>
<mi>x</mi>
<mrow><mtext>H</mtext><mspace width='0.166667em'/><mtext>i</mtext></mrow>
</msub>
</math>
<texmath>x_{\mbox{{\scriptsize {H\,{\sc i}}}}}</texmath>
</formula>
<formula id-text='1' id='uid1' textype='equation' type='display'>
<math mode='display' xmlns='http://www.w3.org/1998/Math/MathML'>
<mrow><mtext>a</mtext><mo>=</mo><mtext>b</mtext><mo>=</mo><mtext>c</mtext></mrow>
</math>
<texmath>\text{a}=\hbox{b}=\mbox{c}
</texmath>
</formula>
If you try to put an attribute pair to the formula or math expression, the behavior depends on the switch. If it is -2, the translation is a <thismathattribute> or <formulaattribute> element. In all other cases, attributes are added to the <formula>, <math> or <texmath> elements (this last element receives both attributes). Example
$\thismathattribute{a}{b}\formulaattribute{c}{d} e$
Here are the translation when the variable is 0, -1, -2 and -3.
<formula type='inline' c='d'>
<math xmlns='http://www.w3.org/1998/Math/MathML' a='b'>
<mi>e</mi>
</math>
</formula>
<texmath c='d' a='b' textype='inline' type='inline'> e</texmath>
<texmath textype='inline' type='inline'>
<thismathattribute><arg>a</arg><arg>b</arg></thismathattribute>
<formulaattribute><arg>c</arg><arg>d</arg></formulaattribute>
e
</texmath>
<formula type='inline' c='d'>
<math xmlns='http://www.w3.org/1998/Math/MathML' a='b'>
<mi>e</mi>
</math>
<texmath c='d' a='b'> e</texmath>
</formula>
In the case where \@nomathml=-3 (see above) Tralics reads a math formula, expanding all commands; the resulting list is then converted twice as an XML expression. A font switch like \mathrm is interpreted as \mml@font@normal. A special marker is inserted in the list, preventing this token to appear in the result. More generally, what follows \@nomathswi appears only in the <math> object, and what follows \@nomathswii appears only in <texmath> object. This mechanism is used whatever the value of \@nomathml. Example
$a \@nomathswi{xy} b \@nomathswii{zt} c$
Here are the translation when the variable \@nomathml is 0, -1, and -3.
<formula type='inline'>
<math xmlns='http://www.w3.org/1998/Math/MathML'>
<mrow><mi>a</mi><mrow><mi>x</mi><mi>y</mi></mrow><mi>b</mi><mi>c</mi></mrow>
</math>
<texmath textype='inline' type='inline'>a b {zt} c</texmath>
</formula>
<formula type='inline'>
<math xmlns='http://www.w3.org/1998/Math/MathML'>
<mrow><mi>a</mi><mrow><mi>x</mi><mi>y</mi></mrow><mi>b</mi><mi>c</mi></mrow>
</math>
<texmath>a b {zt} c</texmath>
</formula>
Other example. Assume that you want to create a command \varPi which is the upper case equivalent of \varpi. This command should have the same translation as \Pi, but should be presented as \varPi in no-mathml mode. Here is a possible definition. Note that "what follows \@nomathswii" was a list in the previous example, and braces are kept in the XML; here is the expansion of \noexpand, thus a control sequence name.
\def\varPi{\@nomathswi\Pi \@nomathswii\noexpand\varPi}
$a+\varPi$
Here are the translation when the variable \@nomathml is -3.
<formula type='inline'>
<math xmlns='http://www.w3.org/1998/Math/MathML'>
<mrow><mi>a</mi><mo>+</mo><mi>Π</mi></mrow>
</math>
<texmath>a+\varPi </texmath>
</formula>
The \nolinebreak command takes an optional argument. It is used to inhibit line break at this position in the paragraph. This command is ignored in Tralics.
The \nonscript command is only valid in math mode. A special item is inserted in the current math list. After all tokens are converted into MathML fragments, if the following token is a <mspace> it will be removed, provided that the current style is scriptstyle or scriptscript style. Example
\def\XX{\nonscript\,}
$a\XX b_{c\XX d} a\XX b_{\textstyle c\XX d} $
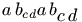
You can prefix the command \nonstopmode with \global. Nothing happens, since batch-mode is the only interaction mode.
Since version 2.15.4, \nonumber is the same as \notag; previously it was ignored.
This command takes one argument and ignores it.
The \nopagebreak command takes an optional argument. It is used to inhibit page break at this position in the text. This command is ignored in Tralics.
In LaTeX, this sets \lineskip, \baselineskip and \lineskiplimit to \normalXXX (see description below). Does nothing in Tralics.
Set by LaTeX to 12pt, updated whenever the font size changes, unused by Tralics.
Set by LaTeX to 1pt, unused by Tralics.
Set by LaTeX to 0pt, unused by Tralics.
Switches to the default color; see \color.
The \normalfont command is a command that selects a font of normal family, series and shape. That is, roman family, medium series and upright shape. It is the same as \rm.
In LateX, it uses \encodingdefault \familydefault \seriesdefault \shapedefault but the last three commands are not implemented in Tralics. Remember that the encoding is always Unicode. There is a comment in the LaTeX source that says: The user interface name for \reset@font is \normalfont.
The \normalsize command is a command that selects a font of normal size. For an example of fonts, see \rm.
The \not command is most often translated by Tralics as \neg (this is wrong). But MathML gives no easy way to negate an operator... There are some hacks: \not=is replaced by \ne. This can be wrong in cases like x_\not=1.
It can be used as boolean negator inside conditionals defined by \ifthenelse.
It can be used as boolean negator (equivalent to \not) inside conditionals defined by \ifthenelse.
We describe here the behavior of version 2.15.4, and following. There are three kinds of math expressions: (a) no equation number, (b) one equation number, and (c) multiple equation numbers (one for each row). An equation number is generated by increasing the equation counter, this creates a label. The command \nonumber inhibits incrementation of the counter, and no tag is produced; for this reason, it has an alias \notag. You can also say \tag{foo}, this inhibits incrementing the equation counter, but creates a tag. Note that a tag implies an anchor, to which a \label can refer.
In Tralics the anchor is associated to the formula. This means: at most one tag, at most one label, and case (c) becomes problematic. See description of the \tag command for details. If the counter \multi@math@label is non-zero, or option -multi_math_label has been used, then the anchor is associated to the row. This means, for each row: at most one tag, at most one label. So: in case (a), \notag is illegal, as well as \tag; in case (b) \notag and \tag{...} inhibit incrementing the equation counter; at most one \tag{...} is allowed; in the case a label is used but no tag is given, then \notag is ignored; case (c) is like (b), but each row is considered as formula. See \multi@math@label for examples.
The \notin command gives a `not in' symbol: <mo>∉</mo> (Unicode U+2209, ∉). See also description of the \smallint command.
If you say \let\foo\@notprerr, then calling \foo provokes the error Can be used only in preamble
You can say \notrivialmath=93, this changes the value of an internal counter (See scanint for details of argument scanning). By default, the value is one, unless you call Tralics with the switch -trivialmath or -notrivialmath. The value C of this counter (modulo 8) is considered. If the first bit of C is set (i.e., if C is odd), then $1^e$, X$^{eme}$ $4^{i\grave{e}me}$ is considered a sequence of trivial math expressions, and translated as 1<hi rend='sup'>e</hi>, or X<hi rend='sup'>e</hi>, or 4<hi rend='sup'>e</hi>, that may be rendered as 1e, Xe, 4e. Expressions that match are formed of an optional sequence of digits, a superscript character, a special exponent; valid exponents are th, rd, rt, st (for English), or e, ieme, eme, ième, ier, er, iemes, ièmes, es, ère, re (for French). The exponent can contain font changes like \small or \rm. As you can see, in French, there may be some transformation, because many people using wrong abbreviations.
If the second bit of C is set (C is 2, 3, 6, 7 modulo 8) then $x$ $1$ $\alpha$ $\pm$ is considered as a set of trivial math formulas, translated into <formula type='inline'><simplemath>x</simplemath></formula> 1 &alpha ±. Note that a formula consisting of a single digit matches two rules. Most, but not all math symbols, produce a non-math value if they are the only token in the formula. Character symbols like '+', '*', are not trivial; exception $-$ is translated as en-dash (Unicode U+2013).
If the third bit of C is set (i.e. C is 4, 5, 6, 7 modulo 8), then $_{foo}$ $^{2+3}$ is considered as a sequence of trivial math expressions and translated as <hi rend='sub'>foo</hi> <hi rend='sup'>2+3</hi>. Candidates are formulas starting with hat or underscore, followed by a character, or a list containing only characters. In the case $^{eme}$, this rule is applied before the rule that says that the translation should be <hi rend='sup'>e</hi>. Font changes are allowed, provided that it is the first token in the list, and the font is one of it, rm, sf, tt and bf, so that $_{\bf foo}$ is the same as \textsubscript{{\bf foo}}.
In some examples above, the expression is compiled like \textsuperscript or \textsubscript (see \rm for how the change the translation of font commands). The default value is 7, and the option -notrivialmath sets the flag to 0.
The \nparallel command is valid only in math mode. It generates <mi>∦</mi> (Unicode U+2226, ∦).
The \nprec command is valid only in math mode. It generates <mi>⊀</mi> (Unicode U+2280, ⊀).
The \nrightarrow command is valid only in math mode. It generates <mi>↛</mi> (Unicode U+219B, ↛).
The \nRightarrow command is valid only in math mode. It generates <mo>⇏</mo> (Unicode U+21CF, ⇏).
The \nsim command is valid only in math mode. It generates <mi>≁</mi> (Unicode U+2241, ≁).
The \nsubseteq command is valid only in math mode. It generates <mi>⊈</mi> (Unicode U+2288, ⊈).
The \nsucc command is valid only in math mode. It generates <mi>⊁</mi> (Unicode U+2281, ⊁).
The \nsupseteq command is valid only in math mode. It generates <mi>⊉</mi> (Unicode U+2289, ⊉).
The \ntriangleleft command is valid only in math mode. It generates <mi>⋪</mi> (Unicode U+22EA, ⋪).
The \ntrianglelefteq command is valid only in math mode. It generates <mi>⋬</mi> (Unicode U+22EC, ⋬)
The \ntrianglelefteqslant command is valid only in math mode. It generates <mi>⋬</mi> (Unicode U+22EC, ⋬).
The \ntriangleright command is valid only in math mode. It generates <mi>⋫</mi> (Unicode U+22EB, ⋫).
The \ntrianglerighteq command is valid only in math mode. It generates <mi>⋭</mi> (Unicode U+22ED ⋭) .
The \ntrianglerighteqslant command is valid only in math mode. It generates <mi>⋭</mi> (Unicode U+22ED; ⋭).
The \nu command is valid only in math mode. It generates a Greek letter: <mi>ν</mi> (Unicode U+3BD, ν). See description of the \alpha command.
Because of the definition \def\null{\hbox{}}, the effect of the \null is to put, on the XML tree, an element that is not visible in the printed output.
The \nullfont command is a reference to a font. It can be used wherever a font is required. However no character is defined in this font, and all parameters are zero. For instance \textfont0=\nullfont is valid.
When you say \nulldelimiterspace=5pt,
then TeX will use 5pt as the width of null delimiters
(for instance \right.; also on the left and right of a
normal fraction, because \over is the same as
\overwidthdelims..).
It is ignored by Tralics.
 (See scandimen for details of argument
scanning).
(See scandimen for details of argument
scanning).
The \number command reads a number (a signed 32bit integer) via the scanint procedure. The expansion of the command is the list of tokens (characters with \catcode 12) of the decimal expansion of the number. In the example that follows, the expansion of \Test is 2.
\def\Test-#174{#1}
\count3=-27
\expandafter\Test\number\count3 4
After the \numberedverbatim command is issued, lines produced by the verbatim environment are preceded by a line number. This command has no effect on the Verbatim environment.
If you say \numberwithin{foo}{bar} then an error is signaled unless both arguments are counters. The first counter is dependent on the second one (reset when stepped). Moreover \thefoo is \thebar.\arabic{foo}. An optional argument can be used, it will replace the \arabic token. This command introduced in Version 2.13.1.
As in the case of ε-TeX, Tralics provides the notion of expressions of type number, dimen, glue or muglue, that can be used whenever a quantity of that type is needed. Such an expression is read by the scanning mechanism; basically scanint and friends are used to read a quantity, and \multiply and friends are used to perform operations. The four commands that can be used are \numexpr, \dimexpr, \glueexpr and \muexpr. They determine a type t, the type of the result, and read an expression, that is followed by an optional \relax (that will be read). When scanning for an operator or the end of an expression, spaces are discarded. An expression consists of one or more terms of type t, that are added or subtracted. A term of type t consists of an initial factor of type t, multiplied or divided by a numeric (integer) factor. Finally, a factor is either a quantity of type t, or a parenthesized expression. Example.
\ifdim \dimexpr(2pt-5pt) *\numexpr 3-3*13/5\relax + 34pt/2=32pt \else\bad\fi
Here the \relax terminates the \numexpr. This is the trace. You will see expr so far when a term is converted into an expression (prefix `='), or after an addition or subtraction (prefix `+' or `-'). You will see term so far after a multiplication or division (prefix '*' or '/') or a scaling (prefix backslash). In the case of a*b/c, a 64bit intermediate product is computed.
[8] \ifdim \dimexpr(2pt-5pt) *\numexpr 3-3*13/5\relax + 34pt/2=32pt +\ifdim1 +scanint for \dimexpr->2 +scandimen for \dimexpr->2.0pt +expr so far for \dimexpr= 2.0pt +scanint for \dimexpr->5 +scandimen for \dimexpr->5.0pt +expr so far for \dimexpr- -3.0pt +scanint for \numexpr->3 +expr so far for \numexpr= 3 +scanint for \numexpr->3 +scanint for \numexpr->13 +scanint for \numexpr->5 +term so far for \numexpr\ 8 +expr so far for \numexpr- -5 +scan for \numexpr= -5 +scanint for \dimexpr->-5 +term so far for \dimexpr* 15.0pt +expr so far for \dimexpr= 15.0pt +scanint for \dimexpr->34 +scandimen for \dimexpr->34.0pt +scanint for \dimexpr->2 +term so far for \dimexpr/ 17.0pt +expr so far for \dimexpr+ 32.0pt +scan for \dimexpr= 32.0pt +scandimen for \ifdim->32.0pt +scanint for \ifdim->32 +scandimen for \ifdim->32.0pt +iftest1 true
Note that 3*13/5 is 8-1/5, and this is rounded to 8. In the case of \divide, the result is truncated. All intermediate expressions are checked for overflow, which is 231 for an integer, and 230 otherwise (in magnitude). This means that dimensions and components of glue must be less than 214 in units of pt, mu or fil.
One important point is that these operations do no side effects, hence can be used inside an \edef. If used out of context, you can see error messages like You can't use `\numexpr' in horizontal mode, (the messages depends on the current mode), in Tralics, the error is Read only variable \numexpr, because these operations are implemented as the value of a read only variable. Example
\def\foo#1#2{\number#1
\ifnum#1<#2, %
\expandafter\foo
\expandafter{\number\numexpr#1+1\expandafter}%
\expandafter{\number#2\expandafter}%
\fi}
\edef\Bar{\foo{7}{13}}
\def\xBar{7, 8, 9, 10, 11, 12, 13}
\ifx\Bar\xBar\else \bad\fi
The \numero and \no commands translate the same as n\textsuperscript{o}\xspace. Before version 2.8.2, it was №, an entity defined by the raweb.
The \Numero and \No commands translate the same as N\textsuperscript{o}\xspace. Before version 2.8.2, it was &Numero;, an entity defined by the raweb.
Thes commands are the negations of \vdash, \vDash, \Vdash,\VDash. They can be used in math mode only. Translation is a <mo> containing a ⊭ (U+22AC; ⊬), ⊭ (Unicode U+22AD, ⊭), ⊮ (U+22AE, ⊮), or ⊯ (U+22AF; ⊯) respectively.
The \nwarrow command is valid only in math mode.
It generates an arrow that points North-West:
<mo>↖</mo> (Unicode U+2196, ↖).
 See description of the \leftarrow command.
See description of the \leftarrow command.
back to home page
© INRIA 2003-2005, 2006
Last modified $Date: 2015/12/02 13:04:59 $