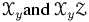
This page contains the description of the following commands
\edef,
\egroup,
\eject,
\ell,
\else,
\em,
\emergencystretch,
\emph,
\@empty,
\emptyset,
\end,
\@@end,
\encodingdefault,
\endcitation,
\endcsname,
\endgraf,
\endgroup,
\endinput,
\endL,
\endline,
\endlinechar,
\endR,
\endsec,
\@endtheorem,
\endv,
\enspace,
\ensuremath,
enumi,
enumii,
enumiii,
enumiv,
\epsfbox,
\epsffile,
\epsfig,
\epsfxsize,
\epsfysize,
\epsilon,
\eqcirc,
\eqno,
\eqref,
\eqsim,
\eqslantgtr,
\eqslantless,
\equal,
\equiv,
\errhelp,
\errmessage,
\error,
\errorcontextlines,
\errorstopmode,
\escapechar,
\eta,
\eth,
\eTeXrevision,
\eTeXversion,
\evensidemargin,
\everycr,
\everybibitem,
\everydisplay,
\everyeof,
\everyjob,
\everyhbox,
\everymath,
\everypar,
\everyvbox,
\everyxbox,
\ExecuteOptions,
\ExecuteOptionsX,
\exhyphenpenalty,
\exists,
\exp,
\expandafter,
\@expandtwoargs,
\ExponentialE,
\externallabels,
\externalref,
\externalcite,
and environments
enumerate,
eqnarray,
eqnarray*,
equation,
equation*.
You can say \edef\foo{bar}. The syntax is the same as \def, but the token list in the body is fully expanded (tokens that come from \the are not expanded).
You can put the prefix \global before \edef, note that \xdef is the same as \global\edef. In the example that follows, the \ifx is true.
{\catcode`\A=12 \catcode`\B=12\catcode`\R=12\gdef\fooval{ABAR}}
{\escapechar=`\A \edef\foo{\string\BAR}\ifx\foo\fooval\else \uerror\fi}
Another example is the following. The \meaning command returns a token list, of the form macro:#1#2->OK OK, and \strip@prefix removes everything before the > sign. What we put in \Bar is a list of five tokens, a space, and four letters of catcode 12.
\makeatletter
\def\strip@prefix#1>{}
\def\foo#1#2{OK OK}
\edef\Bar{\expandafter\strip@prefix\meaning\foo}
For a non-trivial example, see \aftergroup.
The \egroup command is a closing brace of catcode 2. For an example see here.
Behaves like \par, but no page is ejected.
The \ell command is valid only in math mode. It generates a miscellaneous symbol (calligraphic ell): <mi>ℓ</mi> (Unicode U+2113, ℓ). See description of the \ldots command.
The command \else is used in a case like \ifnum 0=0 \somethinguseful \else \whatever \fi. (See \if... for details).
The \em command changes the shape of the current font: if the shape is upright, it is replaced by italics, otherwise by upright. Note that this command is unaware of implicit font changes. Said otherwise, in the title of a section, it is inefficient, since it has no way of knowing in which font the title will be typeset.
You can say \emergencystretch=5pt, as a result TeX will try a third pass in its hyphenation algorithm. Ignored by Tralics. (See scandimen for details of argument scanning).
The \emph command is like \em, except that it takes an argument.
The \@empty command takes no argument, and does nothing. The \empty command is similar. You should not redefine the \@empty command.
The \emptyset command is valid only in math mode. It generates a miscellaneous symbol (empty set): <mi>∅</mi> (Unicode U+2205, ∅). See description of the \ldots command.
This finishes an environment.
See the \begin
command. In principle \end{foo}: (1)
calls \endfoo, (2) checks that the current environment is foo
,
(3) pops the save stack, and (4) executes additional code (for instance,
ignore space that follows). This last step is not yet done
by Tralics. The effect of (3) is to undo all changes that
were local in the environment; in
particular, this changes the name of the current environment.
Let's consider the following code:
\def\foo{\begin{it}}\def\endfoo{\end{it}}
\begin{foo} ok \end{foo} % example1
\def\endbar{\def\@currenvir{bar}}
\begin{it} \end{bar} % example2
\def\endfoo{}
\begin{foo} ok \end{foo} \end{it} % example 3
\def\endfoo#1{}
\begin{foo} ok \end{foo} % exemple 4
\def\endfoo{\show\endfoo}
\begin{foo}
\def\endfoo{\undefined}
\end{foo} % example 5
In the first case, when \end{foo} is seen, the current
environment is it
, and after execution
of \endfoo it will be foo
. This explains why
(2) must come after (1). Note
that \endit is undefined; it is set
to \relax by the \end command, and reset
to undefined by (3). The second example shows how to cheat;
this is invalid in Tralics since the name of the current
environment cannot be changed. You get a
message cannot close environment bar , and the
current environment is still it
.
Example 3 yields an error, of the
form LaTeX Error: \begin{it} on input line 8 ended by
\end{foo} followed by
LaTeX Error: \begin{foo} on input line 8 ended by
\end{it}. The Tralics message are a bit
different: Environment 'it' started at line 8 ended
by \endfoo (this message is also printed for lines 11 and 14)
and Environment 'foo' started at line 8 ended by
\endit.
The next example is incorrect, as
command \endfoo reads some random arguments used for
(2) and (3). This is detected and provokes an error of the
form Illegal end of environment.
In the last example, \endfoo is locally
redefined; but Tralics uses the definition that was active
when \begin{foo} was seen. This means that you will see:
\endfoo=macro: ->\undefined . Note: the stack
contains three open environments: it, foo and foo. You can
say \end{...}
. If the argument is document
this
signifies the end of the job, if the argument is foo
,
then \endfoo is evaluated (this might provoke an
error), if the argument is it
, the stack is popped and an error is
signaled, otherwise an error is signmed and the stack is not popped.
This variable contains the default font encoding; its value is T1 in Tralics, but not used.
This command is used to finish a citation, see \citation.
The \endcsname command is a TeX primitive that marks the end of a \csname command (see \csname). Look at this example:
\def\cmd{csname} \csname foo\csname end\cmd\endcsname
\begin{csname}foo\end{csname}
The first \csname sees `foo', then ask for the expansion of the second \csname. This one sees `end', then the expansion of \cmd, then the \endcsname. The result of the expansion is \endcsname, and this stops the expansion of the first \csname. Hence the first line is the same as \foo.
The second line is equivalant to \begingroup\csname foo\endcsname\endgroup (whith some checks). In LaTeX, this works without problem. In Tralics, this does not work. because the \end token is not expanded, but evaluated. So \csname complains with Invalid token \end found between \csname and \endcsname, and evaluation of \end yields a Extra \endcsname error.
This command is not allowed in internal vertical mode. In regular vertical mode it terminates TeX if the main vertical list is empty and \deadcycles=0. Otherwise, TeX backs up the \end command so that it can be read again; then it exercises the page builder, after appending a box/glue/penalty combination that will force the output routine to act.
In Tralics, things are much easier: all open files are closed, and this should terminate everything. Note that \end is used to finish an environment, so that the TeX primitive is renamed to \@@end.
The \endgraf command is a synonym for \par (note that LaTeX redefines sometimes \par, hence leaves a copy in \@@par. Both \@@par and \endgraf are equivalent to the original \par command).
The \endgroup command is used to terminate a group opened by \begingroup. See \begingroup. If you say \def\foo{}\begin{foo}\endgroup, then LaTeX says nothing, but Tralics complains that something is wrong, because it uses a special token. If you try this
\def\foo{}\def\endfoo#1{\global\let\specialend#1#1}
\begin{foo}
\end{foo}
\show\specialend
you will see something like: \specialend=\endgroup (for env). In the current version of Tralics it is illegal to define \endfoo with an argument,
When Tralics evaluates the \endinput token, it closes the current file (this terminates the job if there is no other open file). For an example, see \InputIfFileExists.
These commands are ε-TeX extensions that indicate the end of a left-to-right or right-to-left region; they are ignored by Tralics.
This command is equivalent to \cr. The TeXbook justifies introducing this command by saying that it is often useful to redefine the meaning of \cr. In Tralics, outside a table, it may provoke the error bad \cr.
The \endlinechar command reads an integer (see scanint for details) that says what character Tralics should insert in the input stream for an end-of-line. The default value is a carriage return (ASCII 13). If the value if not between 0 and 255 (216-1 in the current version), no character is added at the end of a line. In the example below, the translation should give `xy'.
Note that, if a line finishes with \endlinechar=something, TeX has a tendency to ignore one optional space after a number; this space is looked at before the assignment takes place, and could be searched on the line that follows the assignment. In the example below, there is a space after the -1 (without the comment, this space would have been removed.) In the case of `\A, the situation is worse: TeX is in state S, so that spaces after \A are ignored. We inserted a \relax token as remedy.
%The command \testeq checks that its arguments are equal {x\endlinechar=`\A \relax % this \relax is useful \def\foo{a b}\testeq\foo{aAb}% \def\foo{a b}\testeq\foo{aAb}% \endlinechar=`\% % \def\foo{a b}\testeq\foo{ab} \endlinechar=-1 % this comment is useful \def\foo{a b}\testeq\foo{ab} y}
If you say \endsec{\section}, the effect is to end the current section. The argument can be one of: \part \chapter \section \subsection \subsubsection \paragraph \subparagraph, anything else (included an empty argument) is replaced by \part. No new section is started.
Private Tralics command.
This is a special command that prints as \endtemplate.
Same as \kern0.5em.
The \ensuremath command takes one argument, and typesets it in math mode. In the following example, the translation of \test is a calligraphic X with an index y. In both cases, the whole math formula uses the calligraphic font. Note that Tralics uses a normal y, while TeX will use whatever glyph is in the font at the position of a lower-case Y. The definition of \bad is wrong: the expansion of \ensuremath is done outside math mode, hence produces $\relax xx$, so that \bad is $$\relax xx$$.
\def\test{\ensuremath{\cal X_y}}
\test and $\test Z$
\edef\bad{$\ensuremath{xx}$}
Preview: 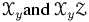
This is an environment in which you can puts items. Nesting such environments is possible, ten counters are reserved for that. See description of the \item command.
These counters are described in the Latex book. There are twenty such counters in Tralics, enumi through enumx and Enumi through Enumx. Lowercase counters are used by the enumerate environment, the other counters by itemize or description. For each counter CTR, LaTeX defines \labelCTR as (\theCTR). This is done (for standard classes) by Tralics for lowercase counters. These quantities are used by Tralics for the label attribute. In the case of counters like Enumi, Enumii, etc, up to level 5, \theCTR is defined in such a way as top obtain 1.2, or 1.5.3.4, etc. The case of the four counters enumi, enumii, enumiii, enumiv is special: the standard classes use the same method as the book class, namely to define \theCTR as \@arabic\c@CTR, \@alph\c@CTR, \@roman\c@CTR and \@Alph\c@CTR, and use a non trivial \p@CTR. In the example below, the id-text of each item is obtained as \p@CTR\theCTR. The string 1(a)iA in the fourth item is what LaTeX typesets for \ref{d}.
\begin{enumerate}
\item a \label{a}
\begin{enumerate}
\item b \label{b}
\begin{enumerate}
\item c \label{c}
\begin{enumerate}
\item d \label{d}
\begin{itemize}
\item u
\begin{itemize}
\item u1
\item u2
\end{itemize}
\item v
\end{itemize}
\end{enumerate}
\end{enumerate}
\end{enumerate}
\end{enumerate}
Translation
<list type='ordered'>
<item id-text='1' id='uid1' label='(1)'><p noindent='true'>a</p>
<list type='ordered'>
<item id-text='1a' id='uid2' label='(a)'><p noindent='true'>b</p>
<list type='ordered'>
<item id-text='1(a)i' id='uid3' label='(i)'><p noindent='true'>c</p>
<list type='ordered'>
<item id-text='1(a)iA' id='uid4' label='(A)'><p noindent='true'>d</p>
<list type='simple'>
<item id-text='1' id='uid5'><p noindent='true'>u</p>
<list type='simple'>
<item id-text='1.1' id='uid6'><p noindent='true'>u1</p></item>
<item id-text='1.2' id='uid7'><p noindent='true'>u2</p></item>
</list>
</item>
<item id-text='2' id='uid8'><p noindent='true'>v</p></item>
</list>
</item></list>
</item></list>
</item></list>
</item></list>
If you say \epsfbox{foo}, the result is the same as if you had said \includegraphics [options] {foo}, where options is formed of width=xx and/or height=yy; here xx is the value of \epsfxsize and yy is the value of \epsfysize. If some value is zero, the corresponding slot is not added to the list. After execution of the command, both values are set to zero (local assignment). See the \includegraphics command for details on how images are processed. Example.
{
\setlength\epsfxsize{50pt}
\setlength\epsfysize{60pt}
\epsfbox{x.ps}
\setlength\epsfysize{70pt}
\epsfbox{x.eps}
\epsfbox{x.epsf}
}
Translation:
<figure height='60.0pt' width='50.0pt' rend='inline' file='x' extension='ps'/> <figure height='70.0pt' rend='inline' file='x' extension='ps'/> <figure rend='inline' file='x' extension='epsf'/>
The \epsffile command is an alternate name of the \epsfbox command.
Instead of saying \epsfig{file=x,width=1} you should say \includegraphics [width=1] {x}. See \includegraphics command. There no difference between \psfig and \epsfig.
This is a reference to dimension register, used by the epsf package, initially set to 0. It indicates the width of the next image. It is reset to zero after usage. See \epsfbox.
This is a reference to dimension register, used by the epsf package, initially set to 0. It indicates the height of the next image. It is reset to zero after usage. See \epsfbox.
The \epsilon command is valid only in math mode. It generates a Greek letter: <mi>ε</mi> (Unicode U+3F5, ϵ). See description of the \alpha command.
If you say \begin{eqnarray} XX \end{eqnarray},
the result is more or less the same as if you say
$$\begin{array}{rcl} XX \end{array}$$.
Lamport says: An equation number is put on every line unless that line has
a \nonumber command
. In Tralics, a label (hence an
equation number) is associated to the formula, and not the individual parts of
it, so that \nonumber is useless. [Using
the -multi-math-label option changes this
behavior, see \multi@math@label ].
Example
\begin{eqnarray}
x & = &17y \\
y & > & a + b + c+d+e+f+g+h+i+j+ \nonumber\\
& & k+l+m+n+o+p
\end{eqnarray}
This is the translation.
<formula id-text='mid1' id='uid1' type='display'>
<math mode='display' xmlns='http://www.w3.org/1998/Math/MathML'>
<mtable displaystyle='true'>
<mtr>
<mtd columnalign='right'><mi>x</mi></mtd>
<mtd><mo>=</mo></mtd>
<mtd columnalign='left'><mrow><mn>1</mn><mn>7</mn><mi>y</mi></mrow></mtd>
</mtr>
<mtr>
<mtd columnalign='right'><mi>y</mi></mtd>
<mtd><mo>></mo></mtd>
<mtd columnalign='left'>
<mrow><mi>a</mi><mo>+</mo><mi>b</mi><mo>+</mo><mi>c</mi><mo>+</mo>
<mi>d</mi><mo>+</mo><mi>e</mi><mo>+</mo><mi>f</mi><mo>+</mo><mi>g</mi>
<mo>+</mo><mi>h</mi><mo>+</mo><mi>i</mi><mo>+</mo><mi>j</mi>
<mo>+</mo></mrow>
</mtd>
</mtr>
<mtr>
<mtd></mtd>
<mtd></mtd>
<mtd columnalign='left'>
<mrow><mi>k</mi><mo>+</mo><mi>l</mi><mo>+</mo><mi>m</mi><mo>+</mo>
<mi>n</mi><mo>+</mo><mi>o</mi><mo>+</mo><mi>p</mi></mrow>
</mtd>
</mtr>
</mtable>
</math>
</formula>
Preview 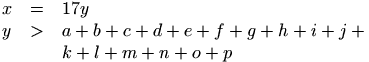
The eqnarray* is the same as eqnarray except it does not generate equation numbers. For Tralics, this means that there is no id. Example.
\begin{eqnarray*}
x & \ll & y_{1} + \cdots + y_{n} \\
& \leq &z
\end{eqnarray*}
Translation
<formula type='display'>
<math mode='display' xmlns='http://www.w3.org/1998/Math/MathML'>
<mtable displaystyle='true'>
<mtr>
<mtd columnalign='right'><mi>x</mi></mtd>
<mtd><mo>≪</mo></mtd>
<mtd columnalign='left'>
<mrow><msub><mi>y</mi> <mn>1</mn> </msub><mo>+</mo><mo>⋯</mo>
<mo>+</mo><msub><mi>y</mi> <mi>n</mi> </msub></mrow>
</mtd>
</mtr>
<mtr>
<mtd></mtd>
<mtd><mo>≤</mo></mtd>
<mtd columnalign='left'><mi>z</mi></mtd>
</mtr>
</mtable>
</math>
</formula>
Preview 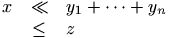 (see also here)
(see also here)
The \eqcirc command is valid only in math mode. It generates <mi>≖</mi> (Unicode U+2256, ≖).
In TeX, the \eqno or \leqno commands are allowed only in display math mode, and it enters non-display math mode for the equation number (which is preceded by the tokens of \everymath, and typeset in a group).
In Tralics, all tokens following \eqno or \leqno are read, and put in a list; the \tag* command is then applied to these tokens. See \tag.
The \eqsim command is valid only in math mode. It generates <mi>≂</mi> (Unicode U+2242, ≂).
The \eqslantgtr command is valid only in math mode. It generates <mi>⪖</mi> (Unicode U+2A96, ⪖).
The \eqslantless command is valid only in math mode. It generates <mi>⪕</mi> (Unicode U+2A95, ⪕).
The \eqref{text} command is the same as (\ref{text}) (this is a very simplified form of the definition of amsmath).
You can use the \equal command inside \ifthenelse in order to compare two token lists. See \ifthenelse for details. It is otherwise undefined.
In Tralics version 2.13.2, there is an equation number for equation, and none for the four other constructs shown here (they produce the same result):
\begin{equation} 0=0 \end{equation}
\begin{equation*} 0=0 \end{equation*}
\begin{displaymath} 0=0 \end{displaymath}
\[ 0=0 \]
$$ 0 = 0 $$
The translation of the first two lines is as follows (the value of the id-text attribute is the translation of \theequation)
<formula id-text='2' id='uid2' type='display'> <math mode='display' xmlns='http://www.w3.org/1998/Math/MathML'> <mrow><mn>0</mn><mo>=</mo><mn>0</mn></mrow> </math> </formula> <formula type='display'> <math mode='display' xmlns='http://www.w3.org/1998/Math/MathML'> <mrow><mn>0</mn><mo>=</mo><mn>0</mn></mrow> </math> </formula>
See also the split environment.
The \equiv command is valid only in math mode. It generates a relation symbol (triple bar equal).: <mo>≡</mo> (Unicode U+2261, ≡). See description of the \le command.
This is a token list, used by TeX in case of an error signalled by \errmessage when the user asks for help. Since Tralics works in batch mode, it does nothing with the list. (See scantoks for the syntax)
This command takes one argument, and uses it to signal an error.
Command with one argument that signals an error.
When you say \errorcontextlines=909, TeX will show only the 909 first error context lines when an error is signaled. This is set to -1 by LaTeX, ignored by Tralics (contexts are not memorized). (See scanint for details of argument scanning).
You can prefix the command \errorstopmode with \global. Nothing happens, since batch-mode is the only interaction mode.
When you say \espacechar=72, then TeX will use character 72 instead of the backslash when printing commands. If the value is not between 1 and 255 (216-1 in the current version), no character will be used. (See scanint for details of argument scanning). Example: \def\foo{\bar}\show\foo. This will print Hfoo=macro: ->Hbar .. If you say \edef\gee{\string\bar}\escapechar=-1\show\gee, you will see gee=macro: ->Hbar., because the \string command uses the current \escapechar, and does not insert a space after command names.
The \eta command is valid only in math mode. It generates a Greek letter: <mi>η</mi> (Unicode U+3B7, η). See description of the \alpha command.
The \eth command is valid only in math mode. It generates a foreign letter: <mi>ð</mi> (Unicode U+F0, ð)
The command \eTeXversion expands to a token list containing the current ε-TeX revison. The counter \eTeXversion returns ε-TeX's major version number. Thus \message{\number\eTeXversion\eTeXrevision} prints something like `2.0'.
This is a dimension, defined by LaTeX, but unused by Tralics.
When you say \everybibitem{\foo\bar}, the token list \foo\bar is inserted whenever Tralics produces a new bibliography item, namely after \bibitem and \citation.
You can say \everycr={foo}, but this has no effect. In TeX, this has as effect to insert the token list after every \cr (or non redundant \crcr). But \cr is not implemented. See scantoks for the syntax.
You can say \everydisplay={foo}, after that the token list foo is added in front of every display math formula, introduced by $$, or \[ or \begin{displaymath}. It has no effect on the translation of environments of the form equation, align, etc. (see \everyhbox for an example).
After \everyeof={foo}, (an extension introduced by ε-TeX), the token list foo is inserted into the input channel when an end-of-file is reached. We give here an example of use. If you say \edef\foo{\scantokens{bar}}, a runaway error is signaled, because an end-of-file is illegal inside \edef. In the code that follows, the \noexpand neutralises the EOF token. Note also that TeX inserts an and-of-line marker just before the EOF marker, this is neutralised by the setting of \endlinechar.
\long\def\safescantokens#1#2{%
\begingroup
\everyeof{\noexpand}%
\endlinechar=-1
\xdef#1{\scantokens{#2}}%
\endgroup
}
\safescantokens\demo{foo}
You can say \everyhbox={\foo\bar}. After that, the token list \foo\bar is inserted in the input stream whenever a \hbox is created (just after the open brace has been read). Don't try \everyhbox={\hbox{x}}. See scantoks for the syntax.
Here is an example of some \every... commands.
{\everyhbox={aa}\everyvbox={bb}\everyxbox={cc} \everymath{\alpha}
\everydisplay{\beta}
\xbox{foo}{\hbox{A\vbox{B}}\hbox{}}
$$ A\hbox{B $C$} D$$
}\xbox{foo}{\hbox{A\vbox{B}}\hbox{}}
$$ A\hbox{B $C$} D$$
This is the translation.
<foo>ccaaAbbBaa</foo>
<formula type='display'>
<math xmlns='http://www.w3.org/1998/Math/MathML'>
<mrow><mi>β</mi><mi>A</mi>
<mrow><mtext>aaB</mtext><mspace width='4.pt'/>
<mrow><mi>α</mi><mi>C</mi></mrow></mrow><mi>D</mi></mrow>
</math>
</formula>
<p noindent='true'><foo>AB</foo></p>
<formula type='display'>
<math xmlns='http://www.w3.org/1998/Math/MathML'><mrow><mi>A</mi>
<mrow><mtext>B</mtext><mspace width='4.pt'/>
<mi>C</mi></mrow><mi>D</mi></mrow>
</math>
</formula>
Here is the content of the transcriot file. Note: in a previous version, Tralics incorrectly inserted the value of everyvbox in the hbox of the math formula.
[420] \xbox{foo}{\hbox{A\vbox{B}}\hbox{}}
{\xbox}
{Push argument 3}
{Text:foo}
{Pop 3: document_v div0_v div3_v argument_v}
{Constructing a box named foo}
+stack: level + 3 for brace entered on line 420
{<everyxbox> cc}
{Push hbox 3}
{\hbox}
{Text:cc}
{Constructing an anonymous box}
+stack: level + 4 for brace entered on line 420
{<everyhbox> aa}
{Push hbox 4}
{\vbox}
{Text:aaA}
{Constructing an anonymous box}
+stack: level + 5 for brace entered on line 420
{<everyvbox> bb}
{Push hbox 5}
{end-group character}
+stack: finish a box of type 2049 % 2049 means: standard
{Text:bbB}
{Pop 5: document_v div0_v div3_v hbox_v hbox_t hbox_t}
+stack: level - 5 for brace from line 420
{end-group character}
+stack: finish a box of type 2049
{Pop 4: document_v div0_v div3_v hbox_v hbox_t}
+stack: level - 4 for brace from line 420
{\hbox}
{Constructing an anonymous box}
+stack: level + 4 for brace entered on line 420
{<everyhbox> aa}
{Push hbox 4}
{end-group character}
+stack: finish a box of type 2049
{Text:aa}
{Pop 4: document_v div0_v div3_v hbox_v hbox_t}
+stack: level - 4 for brace from line 420
{end-group character}
+stack: finish a box of type 2049
{Pop 3: document_v div0_v div3_v hbox_v}
+stack: level - 3 for brace from line 420
[421] $$ A\hbox{B $C$} D$$
{math shift character}
{<everydisplay> \beta }
{reassigning \@curmathfont=0}
+stack: level + 3 for math entered on line 421
{<everyhbox> aa}
+stack: level + 4 for math entered on line 421
{<everymath> \alpha }
Math: $$\beta A\hbox {aaB $\alpha C$} D$$
There is a token list that TeX inserts at the start of the every job. Answer to exercise 24.5 of the TexBook explains how to set this list before the start of the job. This solution is not applicable to Tralics, so that you have to a line like that shown below in the configuration file. (each line overwrites the previous one). You can say \everyjob={foo} (see scantoks for the syntax), this modifies the list, but the new token list is ignored by Tralics.
everyjob="\AtBeginDocument {foo}"
everyjob="\typeout{Hello Word!}"
You can say \everymath={foo}, after that the token list foo is added in front of every non-display math formula (introduced by $, or \( or \begin{math}). (see scantoks for the syntax) (see \everyhbox for an example).
Not implemented. You can say \everypar={foo}, but this has no effect. (See scantoks for the syntax).
You can say \everyvbox={\foo\bar}. After that, the token list \foo\bar is inserted in the input stream whenever a \vbox is created (just after the open brace has been read). See \everyhbox for an example. See scantoks for the syntax.
You can say \everyxbox={\foo\bar}. After that, the token list \foo\bar is inserted in the input stream whenever a \xbox is created (just after the open brace has been read). See \everyhbox for an example. See scantoks for the syntax.
In a class or package file, you define options via
\DeclareOption{foo}{foo-code}. This remembers somewhere that foo
is an option, with value `foo-code'. Later on, you can say
\ExecuteOptions{foo,bar}, this will execute that code associated
to foo and bar; finally, you say \ProcessOptions. This will
execute the code associated to user options, and clean the option table.
 See
\ProcessOptions
for details. The xkeyval package provides
\ExecuteOptionsX that takes key-value pairs as arguments.
See
\ProcessOptions
for details. The xkeyval package provides
\ExecuteOptionsX that takes key-value pairs as arguments.
When you say \hyphenpenalty=100, then TeX will use 100 as penalty for a line break that occurs at discretionary break where the pre-break text is empty (for instance at a dash). Unused by Tralics. (See scanint for details of argument scanning).
The \exists command is valid only in math mode. It generates a miscellaneous symbol: <mo>&exists;</mo> (Unicode U+2203, ∃). See description of the \ldots command.
The \exp command is valid only in math mode. Its translation is a math operator of the same name: <mo form='prefix'>exp</mo>. For an example see the \log command.
The \expandafter command reads a token A, puts it somewhere, calls expand, and inserts the token A. The expand routine reads a token B; if it is a user-defined command, arguments are scanned, and the command B is replaced by the body (with replacement of arguments); if B is a command to be evaluated, (like \par, \hbox, etc) or a character (letter, brace, dollar, etc), it is left unchanged. Finally, B can be something like \string whose purpose is to be expanded. In this case the desired action is performed.
The \expandafter command can be expanded; said otherwise, \expandafter A \expandafter B C is the same as ABc, where c is the expansion of C. Example:
\def\@onlypreamble#1{%
\expandafter\gdef\expandafter\@preamblecmds\expandafter{%
\@preamblecmds\do#1}}
The effect of \@onlypreamble#1 is the same as \gdef\@preamblecmds{XX \do#1}, where XX is the expansion of \@preamblecmds, namely the body of the command. This is an example of how to insert tokens at the end of a command (adding the tokens to the start of the macro is more complicated, because \expandafter\do\expandafter#1 \etc will expand \etc only if #1 is a single token; but it can be anything).
\def\foo#1
{\expandafter\let\csname#1\expandafter\endcsname
\csname end#1\endcsname}%
When you say \foo{bar}, the \let token is stored somewhere and \csname is expanded. Since \csname expands its arguments, it expands the \expandafter; this command puts the \endcsname somewhere and expands the \csname. The result of this expansion is \endbar. After that, \endcsname is considered again, and the first \csname is complete, giving \bar. Hence the expansion is \let\bar\endbar. (this piece of code is extracted from \newenvironment; the purpose is to generate an error if \endbar is defined).
This is the Plain TeX source of \newif.
\outer\def\newif#1{\count@\escapechar \escapechar\m@ne
\expandafter\expandafter\expandafter
\def\@if#1{true}{\let#1=\iftrue}%
\expandafter\expandafter\expandafter
\def\@if#1{false}{\let#1=\iffalse}%
\@if#1{false}\escapechar\count@} % the condition starts out false
\def\@if#1#2{\csname\expandafter\if@\string#1#2\endcsname}
{\uccode`1=`i \uccode`2=`f \uppercase{\gdef\if@12{}}} % `if' is required
We show here the trace of \newif\ifBAR. The interesting point is that there are three \expandafter in a row. If they are followed by \def\foo and \foo expands to \bar, then we get \expandafter\def\bar, so that \foo is expanded twice before \def. But the code is much more subtle than that.
For the first expansion, the command is \@if, it takes two arguments \ifBAR and true, and the expansion is \csname \expandafter \if@ \string #1#2\endcsname. After that \csname is expanded. Hence all the tokens shown above are expanded. Since the second token is \expandafter, the \string token is expanded first. Its results is the list of characters of \ifBAR, with category code `other', without leading backslash (because the escape character is minus one).
The last line of the \newif definition contains \gdef\if@12{}. The \gdef makes the definition global, hence visible outside the group in which the \uccode of 1 and 2 are changed. Thus, we have a command, named \if@, that reads two characters of category 12 (because \uppercase does not change the category code) , and these characters are `if'. (The fact that the characters are 12, and the category code is 12 is a mere coincidence; the fact that \uppercase replaces these characters by `if' and our command \ifBAR starts with `if' is required, unless you like messages like Use of if@ doesn't match its definition. Note that, when the error message is printed, the escape character is still minus one).
Hence, the tokens gathered by the \csname are : `BAR', then `true'. Thus, \newif constructs the command \BARtrue, the \BARfalse. It calls \BARfalse.
[3702] \newif \ifBAR
\newif #1->\count@ \escapechar \escapechar \m@ne
\expandafter \expandafter \expandafter \def \@if #1{true}{\let #1=\iftrue }
\expandafter \expandafter \expandafter \def \@if #1{false}{\let #1=\iffalse }
\@if #1{false}\escapechar \count@
#1<-\ifBAR
{\count255}
+scanint for \count@->92
{changing \count255=0 into \count255=92}
{\escapechar}
+scanint for \escapechar->-1
{changing \count255=0 into \count255=92}
{\expandafter expandafter expandafter}
{\expandafter def @if}
@if #1#2->csname expandafter if@ string #1#2endcsname
#1<-ifBAR
#2<-true
{\expandafter def csname}
{\csname}
{\expandafter if@ string}
if@ if->
{\csname->\BARtrue}
{\def}
{changing BARtrue=relax}
{into BARtrue=macro:->let ifBAR =iftrue }
...
{\let ifBAR iffalse}
{changing ifBAR=undefined}
{into ifBAR=iffalse}
{\escapechar}
+scanint for escapechar->92
The problem is to implement accents. The Tralics code is easy: if the combination accent/accentee exists in Unicode, the translation is that Unicode character, otherwise an error is signalled. In LaTeX, the problem is that the glyph (or sequence of glyphs) must exist in the current font. Hence commands like \\T1\"-a will be used (this command has a digit, a hyphen, a double quote, and two backslashes in its name (the initial backslash is not part of the command name).
If the output font is ecrm1000, then the character é is at position O351, and this is the same position than the character is in the iso-8859-1 character set. It is possible to put the acute accent (position 1 in the font) over the letter e. In the case of a font like cmr10, this is the required method (but the acute accent is in a different slot). For these reasons, the é character is a command, equivalent to \'e. This expands to \T1\'e, or \OT1\'e, depending on the current font encoding. Assume that the current font is cmr, with the OT1 encoding. In this case, the \' command evaluates the following code, with e as argument: \@text@composite \OT1\' #1\@empty \@text@composite {\add@accent {19} {#1}}.
\def\@text@composite#1#2#3\@text@composite{%
\expandafter\@text@composite@x
\csname\string#1-\string#2\endcsname}
\def\@text@composite@x#1{%
\ifx#1\relax
\expandafter\@secondoftwo
\else
\expandafter\@firstoftwo
\fi
#1}
The \@text@composite is a delimited command that takes 3 arguments. The first is \OT1\', the second is the letter, the third is unused (the \@empty token is used in the case of \'{}). It is followed by `generic code' (in this case, code that puts the acute accent, found in position 19, over the letter). The \@text@composite constructs a command named \OT1\'-e. If this command exists, it is called instead of the generic code.
If you call the following command with arguments: {\"}{T1}{a}{228}, you will tell TeX that, for that T1 encoding, the umlaut on the letter a is the character at position 228.
\catcode\z@=11\relax
\def\DeclareTextComposite#1#2#3#4{%
\def\reserved@a{\DeclareTextCompositeCommand#1{#2}{#3}}%
\bgroup
\lccode\z@#4%
\lowercase{%
\egroup
\reserved@a ^^@}}
\catcode\z@=15\relax
The purpose of \lowercase is to convert the integer 228 into a character. The code of \DeclareTextCompositeCommand is rather obvious. Given arguments like {\"}{T1}{a}{ä} it defines \\T1\"-a to be ä. However, we check if the expansion of \T1\" begins with \@text@composite, and if it doesn't, it is redefined. The code below shows these two points. The effect of the four \expandafter tokens is to expand \reserved@a first. This command holds \T1\". Expansion of this command reads one (maybe two) \relax tokens, and produces something. The \@car command is expanded next. It reads all tokens, up to \@nil, returns the first token. The \ifx token is expanded last. It compares the result of \@car and \@text@composite, and takes the appropriate action.
\def\DeclareTextCompositeCommand#1#2#3#4{%
...
\expandafter\expandafter\expandafter\ifx
\expandafter\@car\reserved@a\relax\relax\@nil \@text@composite \else
...
\expandafter\def\csname\expandafter\string\csname
#2\endcsname\string#1-\string#3\endcsname{#4}}
The expansion of \@expandtwoargs\foo\bar\gee is \foo{barval}{geeval} (last two arguments are fully expanded). The result is the same if the input is \@expandtwoargs{\foo}{\bar}{\gee} (for technical reasons, the macro is not expandable). In the example that follows, \@removeelement takes 3 arguments, A, B, C, where A and B are lists, it removes A from B and puts the result in C (the name of a macro). The macro \RM takes two arguments A and C, and uses \@expandtwoargs to get B from the expansion of C (i.e., it removes A from the content of C).
\def\RM#1#2{\@expandtwoargs\@removeelement{#1}{#2}#2}
\def\testfoo#1{\def\xfoo{#1} \ifx\foo\xfoo\else bad \fi} %% test function
\def\foo{A,B C,D,E F}
\RM{D}\foo \testfoo{A,B C,E F}
\RM{D}\foo \testfoo{A,B C,E F}
\RM{B}\foo \testfoo{A,B C,E F}
\RM{B C}\foo \testfoo{A,E F}
\RM{A}\foo \testfoo{E F}
\RM{E F}\foo \testfoo{}
\edef\foo{\zap@space 1 2 345 \@empty 6 7\strip@prefix 1134>89}
\testfoo{123456 789}
The \ExponentialE command is valid only in math mode. It generates <mi>ⅇ</mi> (Unicode U+2147, ⅇ).
The expression \externalcite[x]{y} is handled as \nocite{y}.
back to home page
© INRIA 2003-2005, 2006
Last modified $Date: 2015/12/02 13:02:27 $