TRALICS : a LaTeX to XML translator (G)

If you say \g@addt@macro\foo{bar}, this will have as effect to globally change the macro \foo, by appending to its right the tokens bar. This is similar to \addto@hook, but is more widely used because there is only a small number of token list registers. See also \@cons.

\Game (math symbol)

The \Game command is valid only in math mode. It generates <mi>⅁</mi> (Unicode U+2141, ⅁).

\gamma (math symbol)

The \gamma command is valid only in math mode. It generates a Greek letter: <mi>γ</mi> (Unicode U+3B3, γ). See description of the \alpha command.

\Gamma (math symbol)

The \Gamma command is valid only in math mode. It generates an uppercase Greek letter: <mi>Γ</mi> (Unicode U+393, Γ). See description of the \alpha command.

gather (environment)

This environment has to be used outside math mode, it contains equations separated by \\ commands. If the counter \multi@math@label is non-zero, or if Tralics is called with option -multi_math_label then an anchor is added to every row, its id-text is obtained by incrementing the equation counter. In the example shown, the anchor is attached to the formula and no counter is incremented. (See also here)

<formula id-text='mid1' id='uid1' type='display'>
 <math mode='display' xmlns='http://www.w3.org/1998/Math/MathML'>
  <mtable displaystyle='true'>
   <mtr><mtd><mrow><mn>1</mn><mo>&lt;</mo><mn>2</mn></mrow></mtd></mtr>
   <mtr><mtd><mrow><mn>3</mn><mo>&lt;</mo><mn>4</mn></mrow></mtd></mtr>
  </mtable>
 </math>
</formula>

\gcd (math symbol)

The \gcd command is valid only in math mode. Its translation is a math operator of the same name: <mo form='prefix' movablelimits='true'>gcd</mo>. For an example see the \log command.

\gdef

You can say \gdef\foo{bar}. The syntax is the same as \def, but the definition is global.

\ge, \geq (math symbol)

The \ge command (and is variant \geq) is valid only in math mode. It generates a relation symbol: <mo>≥</mo> (Unicode U+2265, ≥). See description of the \le command.

\genfrac

The \genfrac command is valid only in math mode. It takes six arguments, say L, R, w, s, N, D. The translation is a fraction N over D, with left and right delimiters L and R. The parameter w specifies the width of the fraction rule. It can be omitted. The parameter s specifies the style, it is a number between 0 and 3, interpreted as \displaystyle, \textstyle, scriptstyle, \scriptscriptstyle. It can be empty.

$$\genfrac{}{}{}{}12 % this is \frac 
\genfrac[]{2pt}{2}{aaa}{bbb} % brackets, small, thick 
\genfrac(){0cm}{0}nm % this is \dbinom 
$$

<formula type='display'>
 <math mode='display' xmlns='http://www.w3.org/1998/Math/MathML'>
  <mrow>
   <!-- \genfrac{}{}{}{}12 -->
   <mfrac><mn>1</mn> <mn>2</mn></mfrac>
   <!-- \genfrac[]{2pt}{2}{aaa}{bbb} -->
   <mfenced open='[' close=']'>
    <mstyle scriptlevel='1' displaystyle='false'>
     <mfrac linethickness='2.0pt'>
      <mrow><mi>a</mi><mi>a</mi><mi>a</mi></mrow> 
      <mrow><mi>b</mi><mi>b</mi><mi>b</mi></mrow>
     </mfrac>
    </mstyle>
   </mfenced>
   <!--\genfrac(){0cm}{0}nm -->
   <mfenced open='(' close=')'>
    <mstyle scriptlevel='0' displaystyle='true'>
     <mfrac linethickness='0.0pt'><mi>n</mi> <mi>m</mi></mfrac>
    </mstyle>
   </mfenced>
  </mrow>
 </math>
</formula>

\geqq (math symbol)

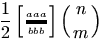
The \geqq command is valid only in math mode; it is a variant of the greater-or-equal symbol: <mo>&geqq;</mo> (Unicode U+2267, ≧).

\geqslant (math symbol)

The \geqslant command is valid only in math mode; it is a variant of the greater-or-equal symbol: <mo>&geqslant;</mo> (Unicode U+2A7E, ⩾). See also description of the \smallint command.

\gets (math symbol)

The \gets command is equivalent to the \leftarrow command: <mo>&leftarrow;</mo> (Unicode U+2190, ←). See also description of the \smallint command.

\gg (math symbol)

The \gg command is valid only in math mode. It generates a relation symbol: <mo>&gg;</mo> (Unicode U+226B, ≫). See description of the \le command.

\ggg (math symbol)

The \ggg command is valid only in math mode. It generates a relation symbol: <mo>&ggg;</mo> (Unicode U+22D9, ⋙).

\gggtr (math symbol)

The \gggtr command is valid only in math mode. It generates a relation symbol: <mo>&ggg;</mo> (Unicode U+22D9, ⋙).

\gimel (math symbol)

The \gimel command is valid only in math mode. It generates <mi>&gimel;</mi> (Unicode U+2137, ℷ).

\global

If you say \global\def... then the definition will be global, unless \globaldefs is negative. The prefix can be used before any assignment, like \let, or \catcode25= \advance\count0. Note that \global\def is the same as \gdef and \global\edef is the same as \xdef.

\globaldefs

When you say \globaldefs=75 (or any positive value), then all following assignments are global. If \globaldefs is negative, then all following assignments are local, even those prefixed with \global. If the value is zero, only those prefixed with \global are global. (See scanint for details of argument scanning).

Example. The following code translates to 023400. Note that the second assignment to \globaldefs is global, so that this variable is negative outside the group.

\count0=0 \count1=0 \count10=0 \count11=0 \count20=0  \count21=0 
{
  \count0=1 \global\count1=2
  \globaldefs=1
  \count10=3 \global\count11=4
  \globaldefs=-1
  \count20=5 \global\count21=6
}
\the\count0 \the\count1 \the\count10 \the\count11 \the\count20 \the\count21 
\globaldefs=0

\glo (Raweb command)

The \glo command takes two arguments. The translation of \glo{a}{b} is the same as \item[a]{b}, namely <label>a</label><item> <p>b</p></item>

glossaire (Raweb environment)

This is an environment in which you can put \glo commands. (do not confuse with the \glossary command). Example.

\begin{glossaire} \glo{x1}{y1}\glo{x2}{y2}\end{glossaire}

<list type='gloss'>
 <head>Glossary</head>
 <label>x1</label>
 <item><p>y1</p></item>
 <label>x2</label>
 <item><p>y2</p></item>
</list>

Note that names are not hard-coded. If the configuration file contains the following

  att_gloss_type = "Gloss"
  xml_gloitem_name = "Glolabel"
  xml_item_name = "Item"
  xml_labelitem_name = "Label"
  xml_list_name = "List"
  xml_head_name = "Head"
  xml_glo_name = "The famous glossary"

<List type='Gloss'>
 <Head>The famous glossary</Head>
 <Glolabel>x1</Glolabel>
 <Item><p>y1</p></Item>
 <Glolabel>x2</Glolabel>
 <Item><p>y2</p></Item>
</List>

\glueexpr (e-TeX extension)

\glueshrink (e-TeX extension)

\glueshrinkorder (e-TeX extension)

\gluestretch (e-TeX extension)

\gluestretchorder (e-TeX extension)

The commands \gluestretchorder, \glueshrinkorder, \gluestretch, \glueshrink can be used when some internal quantity is scanned, for instance after \the. They read some glue and return one part of the glue, it can be the stretch order or the shrink order (an integer between 0 and 3), or the stretch or shrink value (as a dimension). In the case of 3pt plus 4pt minus 5pt, the stretch value is 4pt, the shrink value is 5pt, the strech and shrink orders are zero. The value 3pt can be obtained by converting the glue to a dimension. In the case of 3pt plus 4fil minus 5fill, the values are the same the stretch order is one, the shrink order is 2. Order 3 is obtained when filll is used.

The commands \gluetomu, \mutoglue read and return some glue. The eTeX manual says: glue is converted into muglue and vice versa by simply equating 1pt with 1mu. In the example here we use the commands described above, and store them somewhere.

\muskip0 = 18mu plus 36mu minus 1 fill
\skip0 = 10pt plus 20pt minus 1 fil
\edef\uselater{%
\the\muskip0,%
\the\mutoglue\muskip0,%
\the\skip0,%
\the\gluetomu\skip0,%
\the\mutoglue\gluetomu\skip0,%
\the\glueshrink\skip0,%
\the\gluestretch\skip0,%
\the\glueshrinkorder\skip0,%
\the\gluestretchorder\skip0}

The command \xoo defined here contains the same characters as \uselater. The non-trivial point is that all characters produced by \the are of category code 12.

{\let\GDEF\gdef\let\XDEF\xdef\def\S{ }
 \catcode`m=12 \catcode`u=12 \catcode`p=12 \catcode`f=12  
 \catcode`i=12  \catcode`l=12 \catcode`n=12 \catcode`i=12 \catcode`s=12 
 \catcode`t=12 
 \GDEF\MU{mu}\GDEF\PT{pt}\GDEF\FIL{fil}\GDEF\FILL{fill}%
 \GDEF\PLUS{plus}\GDEF\MINUS{minus}
\XDEF\xoo{18.0\MU\S \PLUS\S 36.0\MU\S \MINUS\S 1.0\FILL,%
18.0\PT\S \PLUS\S 36.0\PT\S \MINUS\S 1.0\FILL,%
10.0\PT\S \PLUS\S 20.0\PT\S \MINUS\S 1.0\FIL,% 
10.0\MU\S \PLUS\S 20.0\MU\S \MINUS\S 1.0\FIL,%
10.0\PT\S \PLUS\S 20.0\PT\S \MINUS\S 1.0\FIL,%
1.0\PT,20.0\PT,1,0}}

The command \yoo defined here contains the same characters and same category codes as \uselater.

\edef\yoo{\detokenize{18.0mu plus 36.0mu minus 1.0fill,%
18.0pt plus 36.0pt minus 1.0fill,%
10.0pt plus 20.0pt minus 1.0fil,% 
10.0mu plus 20.0mu minus 1.0fil,%
10.0pt plus 20.0pt minus 1.0fil,%
1.0pt,20.0pt,1,0}}
\ifx\yoo\xoo\else\bad\fi

\gluetomu (e-TeX extension)

\gnapprox (math symbol)

The \gnapprox command is valid only in math mode; it is a variant of the greater-or-equal symbol: <mo>&gnapprox;</mo> (Unicode U+2A8A, ⪊).

\gneq (math symbol)

The \gneq command is valid only in math mode; it is a variant of the greater-or-equal symbol: <mo>&gneq;</mo> (Unicode U+2A88, ⪈).

\gneqq (math symbol)

The \geqq command is valid only in math mode; it is a variant of the greater-or-equal symbol: <mo>&gneqq;</mo> (Unicode U+2269, ≩).

\gnsim (math symbol)

The \gnsim command is valid only in math mode; it is a variant of the greater-or-equal symbol: <mo>&gnsim;</mo> (Unicode U+22E7, ⋧).

\@gobble, \@gobbletwo, \@gobblefour

The \@gobble command reads one argument and does nothing with it. In the same fashion \@gobbletwo and \@gobblefour read two and four arguments.

\goodbreak

In Tralics, the \goodbreak command is the same as \par. In LaTeX, it adds also some penalty (value -500).

\grabenv (Tralics command)

Inside an environment, you can say \grabenv\foo; in this case, Tralics will collect all tokens until finding the end of the environment, and put them (globally) in the command \foo. In the following example, the last line produces two errors, because because \grabenv is not followed by a valid command name and is outside an environment.

\newenvironment {simple}{A}{B} 
\newenvironment {grab}{C}{D\grabbed} 

Test grabenv
\begin{grab}x\grabenv\grabbed \begin{simple}yz\end{simple}t\end{grab}
\grabbed=\grabenv.OK

Test grabenv
CxDAyzBt
AyzBt=<error n='\grabenv' l='180' c='bad definition'/><error n='\grabenv' l='180' c='\grabenv must be used in an environment'/>OK.

\grave

The \grave command puts a grave accent over a kernel. It works only in math mode. See also the \acute command.

\gtrapprox (math symbol)

The \gtrapprox is valid in math mode only; translation is <mo>&gtrapprox;</mo> (Unicode U+2A86, ⪆).

\gtrdot (math symbol)

The \gtrdot is valid in math mode only; translation is <mo>&gtrdot;</mo> (Unicode U+22D7, ⋗).

\gtreqless (math symbol)

The \gtreqless is valid in math mode only; translation is <mo>&gtreqless;</mo> (Unicode U+22DB, ⋛).

\gtreqqless (math symbol)

The \gtreqqless is valid in math mode only; translation is <mo>&gtreqqless;</mo> (Unicode U+2A8C, ⪌).

\gtrless (math symbol)

The \gtrless command gives a greater/less than symbol. It works only in math mode: <mo>&gtrless;</mo> (Unicode U+2277, ≷). See also description of the \smallint command.

\gtrsim (math symbol)

The \gtrsim is valid in math mode only; translation is <mo>&gtrsim;</mo> (Unicode U+2273, ≳).

guillemets (environment)

If you say \begin{guillemets}xxx\end{guillemets}, it is the same as if you had said «xxx». But in a future version of the software the environment may produce much nicer results.

\guillemotleft

The \guillemotleft command translates into « or «. For more info see the latin supplement characters.

\guillemotright

The \guillemotright command translates into » or ». For more info see the latin supplement characters.

\gsavekeys, \gdelsavekeys, \gunsavekeys

\gpresetkeys, \gdelpresetkeys, \gunpresetkeys

All commands, alphabetic order; letter G

\g@addto@macro