Log Euclidean Metrics: Description
The DTI Track module provides all necessary tools for in-deep DT-MRI analysis and fiber tracking. However, the processing of this type of data (i.e., symmetric positive-definite matrices) has proved difficult in recent years.
Usual Euclidean operations on matrices suffer from many defects on tensors, which have led to the use of many ad hoc methods. Recently, affine-invariant Riemannian metrics have been proposed as a rigorous and general framework in which these defects are corrected. These metrics have excellent theoretical properties and provide powerful processing tools, but also lead in practice to complex and slow algorithms. To remedy this limitation, a new family of Riemannian metrics called Log-Euclidean is used in MedInria. They also have excellent theoretical properties and yield similar results in practice, but with much simpler and faster computations. This new approach is based on a novel vector space structure for tensors. In this framework, Riemannian computations can be converted into Euclidean ones once tensors have been transformed into their matrix logarithms.
An anisotropic regularization can also be applied in the DTI Track module of MedINRIA, it is optional and may take time.
Screenshots
 Geodesic interpolation of two tensors [3]. Left:
Geodesic interpolation of two tensors [3]. Left: interpolated tensors.
Right: graphs of the determinants
of the interpolated tensors.
Top: linear interpolation on coefficients.
Middle: affine-invariant
interpolation.
Bottom: Log-Euclidean interpolation. The coloring of ellipsoids is based on the direction of
dominant eigenvectors, and was only added to enhance the contrast of tensor images. Note the characteristic
swelling effect observed in the Euclidean case due to a parabolic interpolation of determinants. This effect
is not present in both Riemannian frameworks since determinants are monotonically interpolated. Note also
that Log-Euclidean means are more anisotropic their affine-invariant counterparts.
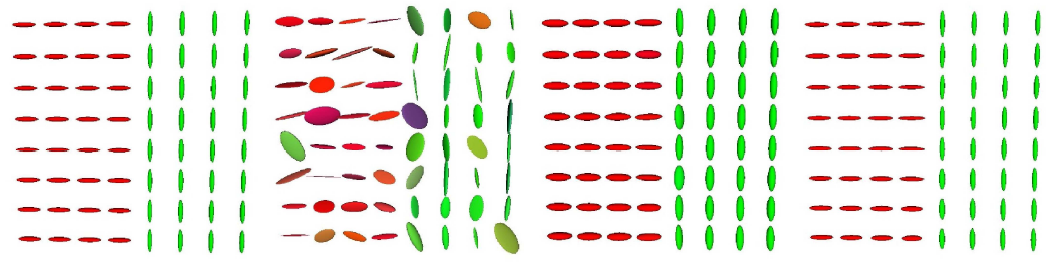 Regularization of a synthetic DTI slice [3]. Left:
Regularization of a synthetic DTI slice [3]. Left: original synthetic data.
Middle Left: noisy
data.
Middle Right: Euclidean regularization.
Right: Log-Euclidean regularization. The original data
is correctly reconstructed in the Log-Euclidean case, as opposed to the Euclidean case where the result is
marred by the swelling effect.
References
-
Pierre Fillard,
Vincent Arsigny,
Xavier Pennec,
and Nicholas Ayache.
Clinical DT-MRI Estimation, Smoothing and Fiber Tracking with Log-Euclidean Metrics.
IEEE Transactions on Medical Imaging,
26(11):1472-1482,
November 2007.
Note: PMID: 18041263.

 [bibtex-entry]
[bibtex-entry]
-
Vincent Arsigny,
Pierre Fillard,
Xavier Pennec,
and Nicholas Ayache.
Geometric Means in a Novel Vector Space Structure on Symmetric Positive-Definite Matrices.
SIAM Journal on Matrix Analysis and Applications,
29(1):328-347,
2006.


 Keyword(s): DT-MRI,
Tensors,
Riemannian geometry,
Lie groups,
interpolation,
Log-Euclidean metrics.
[bibtex-entry]
Keyword(s): DT-MRI,
Tensors,
Riemannian geometry,
Lie groups,
interpolation,
Log-Euclidean metrics.
[bibtex-entry]
-
Vincent Arsigny,
Pierre Fillard,
Xavier Pennec,
and Nicholas Ayache.
Log-Euclidean Metrics for Fast and Simple Calculus on Diffusion Tensors.
Magnetic Resonance in Medicine,
56(2):411-421,
August 2006.
Note: PMID: 16788917.

 Keyword(s): DT-MRI,
Tensors,
Riemannian geometry,
Lie groups,
interpolation,
Log-Euclidean metrics.
[bibtex-entry]
Keyword(s): DT-MRI,
Tensors,
Riemannian geometry,
Lie groups,
interpolation,
Log-Euclidean metrics.
[bibtex-entry]
-
Vincent Arsigny,
Olivier Commowick,
Xavier Pennec,
and Nicholas Ayache.
A Log-Euclidean Framework for Statistics on Diffeomorphisms.
In Proc. of the 9th International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI'06), Part I,
number 4190 of LNCS,
pages 924-931,
2-4 October 2006.
Note: PMID: 17354979.

 Keyword(s): Non-rigid registration,
Lie groups,
Diffeomorphisms,
Log-Euclidean metrics,
Magnetic Resonance Imaging.
[bibtex-entry]
Keyword(s): Non-rigid registration,
Lie groups,
Diffeomorphisms,
Log-Euclidean metrics,
Magnetic Resonance Imaging.
[bibtex-entry]

