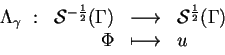


Next: Résultats d'identifiabilité
Up: No Title
Previous: Introduction
L'application visée par ces travaux concerne le problème
d'identification de fissures dans une structure à partir de
données surdéterminées sur le bord.
Cette application s'inscrit dans un domaine du contrôle
industriel : le contrôle non destructif des matériaux.
Plusieurs modèles physiques correspondent aux différentes
techniques de contrôle. Nous retiendrons dans le cadre de
notre étude celles pour lesquelles le phénomène est
modélisé par l'opérateur de Laplace (données thermiques
stationnaires, élastostatique...).
Le principe de ces méthodes est d'imposer une condition sur le
bord extérieur de la pièce que l'on veut contrôler (par
exemple en imposant un flux de chaleur 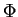 dans le cas du contrôle
par données thermiques) et de mesurer la réponse u du matériau
(température dans ce même cas).
dans le cas du contrôle
par données thermiques) et de mesurer la réponse u du matériau
(température dans ce même cas).
La pièce à examiner occupant le domaine plan D, on modélisera
la fissure par une courbe 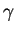 à l'intérieur du domaine.
Le problème direct correspondant est alors décrit ainsi :
à l'intérieur du domaine.
Le problème direct correspondant est alors décrit ainsi :
 |
(1.1) |
où D est un ouvert borné simplement connexe dans le plan
complexe
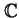 ,
,
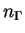 désigne le vecteur unitaire normal
à
désigne le vecteur unitaire normal
à 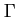 sortant,
sortant, 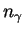 un vecteur unitaire normal
à
un vecteur unitaire normal
à 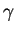 et les points
et les points  et
et 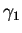 sont les
deux extrémités de la fissure
sont les
deux extrémités de la fissure 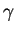 .
Pour tout voisinage assez petit d'un point de
.
Pour tout voisinage assez petit d'un point de 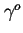 ,
on peut
définir deux régions distinctes séparées par
,
on peut
définir deux régions distinctes séparées par 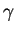 .
La quantité
.
La quantité 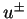 introduite ci-dessus désigne les
déterminations de la quantité u, selon que l'on tend vers
un point de
introduite ci-dessus désigne les
déterminations de la quantité u, selon que l'on tend vers
un point de 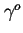 par le ``côté'' + ou - (c.f.
figure 1.1).
par le ``côté'' + ou - (c.f.
figure 1.1).
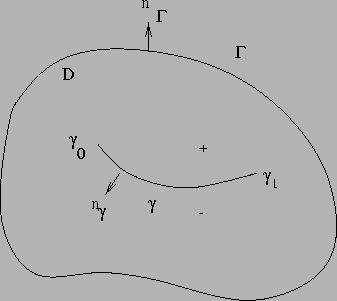
Figure 1.1:
Le domaine D.
#1#2#3#4#5
@font#1#2pt
#3#4#5
|
Comme l'indique la troisième relation dans (1.1), le flux
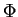 est nul sur la fissure
est nul sur la fissure 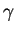 ,
ce qui signifie que celle-ci
est parfaitement isolante (et induit donc une discontinuité dans
la température) mais on notera que par conjugaison harmonique, ce
problème peut se ramener au cas d'un conducteur parfait
(conductivité infinie).
,
ce qui signifie que celle-ci
est parfaitement isolante (et induit donc une discontinuité dans
la température) mais on notera que par conjugaison harmonique, ce
problème peut se ramener au cas d'un conducteur parfait
(conductivité infinie).
Pour que ce problème direct admette une solution, il faut que la
circulation du flux 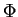 soit nulle, ce qui s'exprime par la condition
soit nulle, ce qui s'exprime par la condition
D'autre part, le problème étant Neumann pur, on peut remarquer
que toute solution u du problème restera solution à une constante
additive près. On ajoutera donc la condition de normalisation
afin de sélectionner une solution.
Le problème de contrôle que nous souhaitons résoudre est le
problème inverse associé au problème (1.1), lorsque l'on ne
connaît pas la fissure 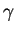 et qu'on dispose pour l'identifier
de données surdéterminées sur le bord extérieur
et qu'on dispose pour l'identifier
de données surdéterminées sur le bord extérieur 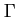 ,
sous la forme de couples (u,
,
sous la forme de couples (u,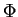 ).
).
Pour déterminer sous quelles conditions ce problème inverse
est bien posé et en proposer une méthode de résolution, il
nous faut examiner les trois points suivants :
-

- Identifiablité
Pour p>0, on notera
 l'espace de Sobolev sur un
domaine D de
l'espace de Sobolev sur un
domaine D de
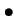 .
Cette définition est étendue pour
p<0 par dualité de manière classique (voir par
exemple [32] pour plus de détails).
.
Cette définition est étendue pour
p<0 par dualité de manière classique (voir par
exemple [32] pour plus de détails).
Définissons, pour une fissure 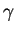 ,
l'opérateur de
Poincaré-Steklov
,
l'opérateur de
Poincaré-Steklov
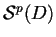 associé
associé
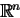 |
(1.4) |
Un résultat d'identifiabilité pour la fissure consiste à prouver
que l'opérateur qui à 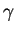 associe
associe
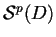 est
injectif.
est
injectif.
Toutefois, dans la mesure où l'on ne dispose au plus que d'un
ensemble fini de couples 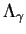 ,
il nous faut un résultat plus
fort.
On ne pourra en effet assurer l'identifiabilité que si, pour un
flux
,
il nous faut un résultat plus
fort.
On ne pourra en effet assurer l'identifiabilité que si, pour un
flux 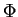 donné (ou pour un ensemble fini de flux), l'opérateur
associé
donné (ou pour un ensemble fini de flux), l'opérateur
associé
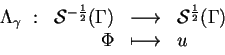 |
(1.5) |
(où 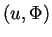 est l'ensemble des fissures admissibles dans D) est
injectif.
est l'ensemble des fissures admissibles dans D) est
injectif.


- Stabilité
Une fois que l'on a la première condition remplie, il convient de
s'assurer de la stabilité de la solution par rapport aux données.
Pour cela, il est nécessaire que, pour le flux 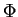 choisi et
choisi et
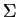 défini comme ci-dessus, l'opérateur inverse
défini comme ci-dessus, l'opérateur inverse
 |
(1.6) |
soit continu (pour une topologie préalablement choisie).

- Identification
Lorsque les deux conditions précédentes sont remplies, ce problème
est bien posé au sens d'Hadamard et l'on peut aborder la question
de l'identification. Il s'agit de définir un procédé d'inversion
(un ou plusieurs flux 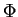 et l'opérateur
et l'opérateur
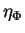 associé)
afin de retrouver la localisation et la forme de la fissure à partir
de la réponse du sytème (la température, ici) au flux
associé)
afin de retrouver la localisation et la forme de la fissure à partir
de la réponse du sytème (la température, ici) au flux 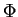 choisi.
choisi.



Next: Résultats d'identifiabilité
Up: No Title
Previous: Introduction
Frederic Mandrea
2001-01-21
![]() dans le cas du contrôle
par données thermiques) et de mesurer la réponse u du matériau
(température dans ce même cas).
dans le cas du contrôle
par données thermiques) et de mesurer la réponse u du matériau
(température dans ce même cas).
![]() à l'intérieur du domaine.
Le problème direct correspondant est alors décrit ainsi :
à l'intérieur du domaine.
Le problème direct correspondant est alors décrit ainsi :
![]() et qu'on dispose pour l'identifier
de données surdéterminées sur le bord extérieur
et qu'on dispose pour l'identifier
de données surdéterminées sur le bord extérieur ![]() ,
sous la forme de couples (u,
,
sous la forme de couples (u,![]() ).
).

 l'espace de Sobolev sur un
domaine D de
l'espace de Sobolev sur un
domaine D de