


Next: Résultats de stabilité
Up: Détection de fissures
Previous: Détection de fissures
Ce problème a été initialement introduit par A. Friedman et
M. Vogelius. Dans un article [28] publié en 1989, ils
prouvent un premier résultat d'identifiabilité dans le cas d'une
fissure unique intérieure. Il y est établi que le choix de
deux flux 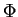 particuliers sur le bord du domaine suffit pour
déterminer de manière unique la présence d'une fissure C2,
et que ce nombre de flux est le nombre minimal.
particuliers sur le bord du domaine suffit pour
déterminer de manière unique la présence d'une fissure C2,
et que ce nombre de flux est le nombre minimal.
Ce résultat a connu par la suite plusieurs généralisations
pour le cas, non plus d'une seule fissure, mais de collections
de fissures dans le domaine D.
Dans l'article [24] de K. Bryan et M. Vogelius, on trouve
une preuve de l'identifiabilité de n fissures par n+1 flux,
résultat renforcé par G. Alessandrini et A. D. Valenzuela
dans [6] ainsi que par H. Kim et J. K. Seo [36]
qui démontrent des résultats d'identifiabilité avec seulement
deux flux (résultat minimal).
Les techniques de preuves employées dans ces travaux reposent
sur une étude fine des courbes de niveau de la solution.
Ainsi, sous les hypothèses idoines de régularité, on voit
que le choix a priori de deux flux particuliers permet d'obtenir
l'unicité des mesures extérieures par rapport aux fissures
dans de nombreux cas.
On notera par ailleurs les résultats d'identifiabilité obtenus
pour un problème connexe au nôtre : dans le cas où l'on ne
dispose de mesures que sur une partie du bord et que l'on cherche
à identifier une fissure atteignant la frontière extérieure
du domaine (on parle dans ce cas d'une fissure débouchante).
S. Andrieux, A. Ben Abda et M. Jaoua démontrent dans [10] un
résultat d'unicité à partir d'un unique flux particulier.
Enfin, on trouvera un résultat traitant le cas de plusieurs
fissures débouchantes dans les travaux de A. R. Elcrat, V. Isakov
et O. Neculoiu [27].



Next: Résultats de stabilité
Up: Détection de fissures
Previous: Détection de fissures
Frederic Mandrea
2001-01-21