| |
(1.7) |
Dans notre cadre de travail, on distingue deux familles de méthodes d'identification :
L'approche présentée dans l'article [48], F. Santosa et
M. Vogelius considèrent le problème dual au nôtre :
Pour que le problème soit bien posé, on y ajoute les conditions
d'existence et de normalisation suivantes :
| (1.8) |
 |
(1.10) |
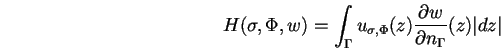 désigne
la solution de (1.7) et (1.9) avec
désigne
la solution de (1.7) et (1.9) avec  construite comme suit :
construite comme suit :
| (1.12) |
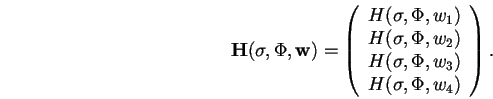 ,
il est possible
d'autre part de se doter de mesures pour la fonction :
,
il est possible
d'autre part de se doter de mesures pour la fonction :
| (1.13) |
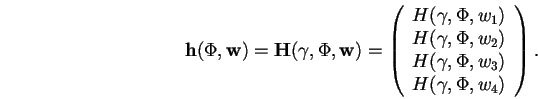 où
où | (1.14) |
Sur la partie gauche des figures, on voit le segment choisi comme fissure initiale au début de chaque itération ((a) et (b) indiquent la première puis la seconde itération) ainsi que les positions des électrodes (les carrés) pour que le flux soit maximalement sensible à chaque itération.
La partie de droite montre d'une part la vraie fissure en pointillés, et d'autre part la position de la fissure à la fin de l'itération. Comme on le voit, si le point de départ est bien choisi, la convergence peut être assez rapide.
Cette approche permet de déterminer assez précisemment la position
d'une fissure rectiligne. Elle requiert toutefois un coût important
de par les résolutions successives du problème direct qu'elle
effectue. On notera par ailleurs que pour exprimer la dérivée de la
fonctionnelle, les auteurs supposent que ![]() est assez proche
de
est assez proche
de ![]() ,
d'où l'importance de disposer de bonnes conditions
initiales dans l'algorithme.
,
d'où l'importance de disposer de bonnes conditions
initiales dans l'algorithme.
Cette méthode, introduite par S. Andrieux et A. Ben Abda dans [9], consiste à comparer la réponse de la pièce fissurée avec celle d'une pièce saine de mêmes caractéristiques.
Soit D l'ouvert occupé par la structure à contrôler, rappelons
alors le problème direct correspondant :
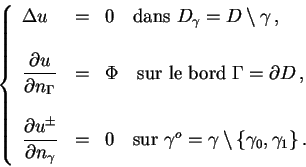 |
(1.16) |
Si la fissure est plane dans un domaine 3D (ou rectiligne dans un
domaine 2D), la normale ![]() est indépendante du point x de
est indépendante du point x de
![]() .
On peut alors la déterminer par les résultats suivants.
.
On peut alors la déterminer par les résultats suivants.
Définissons la fonctionnelle d'écart à la réciprocité
(RG = Reciprocity Gap) comme étant
![\begin{displaymath}RG_{[\Phi,h]}(v)=\int_{\Gamma}{\left(\Phi(z) v(z) - \frac{\partial v}
{\partial n_\Gamma}(z)h(z)\right)\vert dz\vert}
\end{displaymath}](img60.gif) |
(1.17) |
![]()
Une fois la normale N déterminée par cette proposition, on
considère un nouveau repère orthonormal direct (O,T,V,N)de telle sorte qu'en associant les coordonnées
(X1,X2,X3)à ce nouveau repère, le plan ![]() a pour équation X3-C=0.
a pour équation X3-C=0.
On achève en déterminant C avec la proposition suivante :
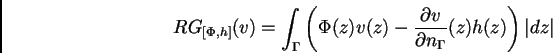
Une fois le plan de la fissure identifié, il reste alors à
déterminer la fissure elle-même dans le plan.
Dans ce but, les auteurs décrivent une méthode constructive
d'identification. Celle-ci considère la prolongation de la fonction
de saut
![]() dans le domaine
dans le domaine
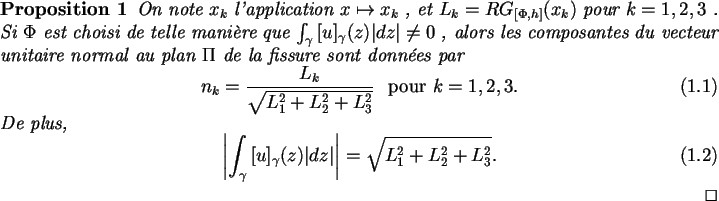 ,
et
cherche à déterminer son support.
,
et
cherche à déterminer son support.
Pour cela, on utilise une décomposition dans une base Hilbertienne
(la base de Fourier est proposée dans cet article) et l'on calcule
les coefficients à l'aide de la fonctionnelle RG. Compte tenu des
oscillations de telles décompositions, on fixe un seuil 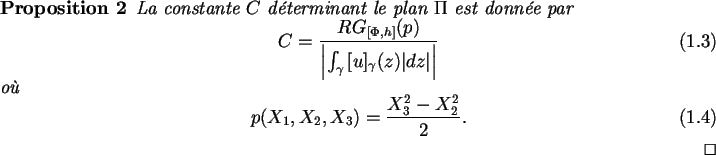 arbitraire et on approxime le support de
arbitraire et on approxime le support de
![]() par
l'ensemble
par
l'ensemble
![]() .
.
Les auteurs présentent finalement le résultat d'identifiabilité
suivant :
![]()
Dans un article en préparation [22], A. Ben Abda et M. Kallel
étendent ces travaux et présentent des résultats numériques.
La base hilbertienne utilisée dans cet article n'est pas la base de
Fourier mais la base de Legendre, celle-ci présentant des oscillations
moindres hors du support et permet de réduire le seuil 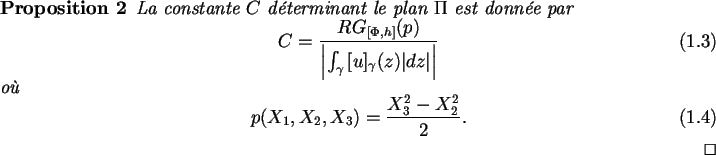 pour
obtenir une meilleure convergence du support vers la fissure.
pour
obtenir une meilleure convergence du support vers la fissure.
Cette approche par la fonctionnelle d'écart à la réciprocité
présente de nombreux avantages : Il s'agit d'une méthode
semi-explicite, ce qui permet d'obtenir les informations sur la
fissure en un temps bien moindre que celui requis par un algorithme
itératif.
De plus, cette approche ne suppose pas pour fonctionner que la fissure
soit nécessairement connexe et reste robuste par rapport au bruit
sur les mesures au bord. Les courbes montrées dans la figure 1.3
montrent la reconstruction de
![]() et de son support pour un flux
identifiant (egal à 1 dans le demi-plan supérieur et -1 dans
le demi-plan inférieur). On voit que le seuillage permet d'obtenir
une bonne identification du support. Il est important de souligner
que cette méthode présente une bonne robustesse par rapport au
bruit sur les mesures.
et de son support pour un flux
identifiant (egal à 1 dans le demi-plan supérieur et -1 dans
le demi-plan inférieur). On voit que le seuillage permet d'obtenir
une bonne identification du support. Il est important de souligner
que cette méthode présente une bonne robustesse par rapport au
bruit sur les mesures.
|
[Reconstruction de
|
Cette méthode non itérative, présentée par M. Brühl, M. Hanke et M. Pidcock dans [23], ne requiert pas de résolution du problème direct excepté pour un premier calcul de l'opérateur de Poincaré-Steklov tel que défini en (1.4) mais correspondant au domaine sain.
A l'aide d'une factorisation de la différence entre l'opérateur
![]() associé au domaine sain D et celui associé au domaine
fissuré
associé au domaine sain D et celui associé au domaine
fissuré
![]() ,
les auteurs définissent un test simple
et peu coûteux permettant de déterminer si un arc de courbe est
inclus dans la fissure
,
les auteurs définissent un test simple
et peu coûteux permettant de déterminer si un arc de courbe est
inclus dans la fissure ![]() .
Pour présenter ces résultats, il
convient d'ajouter à nos notations introduites en (1.15) quelques
définitions et notations utilisées dans l'article.
.
Pour présenter ces résultats, il
convient d'ajouter à nos notations introduites en (1.15) quelques
définitions et notations utilisées dans l'article.
Notons
 le support du flux
le support du flux ![]() sur
le bord extérieur. On définit l'espace
sur
le bord extérieur. On définit l'espace
| (1.18) |
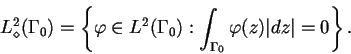 |
(1.19) |
| (1.20) |
| (1.21) |
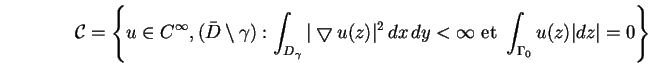 comme étant le complémentaire orthogonal de
comme étant le complémentaire orthogonal de
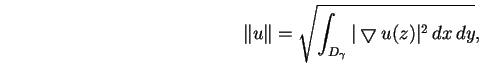 dans
dans
| (1.22) |
| (1.23) |
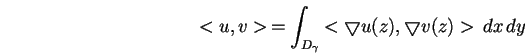 ,
et
,
et
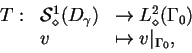 |
(1.24) |
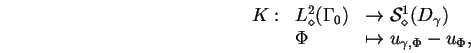 désignent les réponses du système au
flux
désignent les réponses du système au
flux
Les auteurs définissent et prouvent une factorisation de l'opérateur
défini par la différence entre ![]() et
et
![]() ,
sous
forme d'un produit de deux opérateurs adjoints dans le théorème
suivant :
,
sous
forme d'un produit de deux opérateurs adjoints dans le théorème
suivant :
![]()
Cette factorisation étant établie, on a alors le résultat
suivant :
![]()
Enfin, en remarquant que
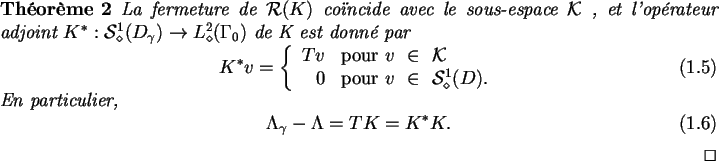 ,
ce thèorème se traduit par le fait que, pour toute fonction
,
ce thèorème se traduit par le fait que, pour toute fonction
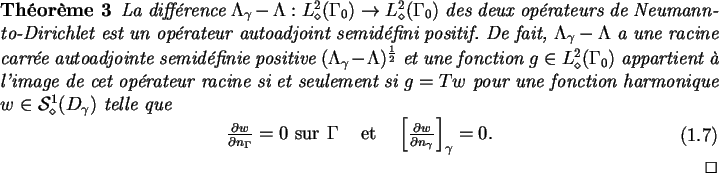 ,
on a
,
on a
![]() si g=T w pour une certaine fonction
si g=T w pour une certaine fonction
![]() .
.
La procédure d'identification consiste à construire la fonction vsuivante.
Soit ![]() une courbe dans D, notons
une courbe dans D, notons
![]() ,
et définissons v1 par un potentiel double-couche comme suit :
,
et définissons v1 par un potentiel double-couche comme suit :
| (1.25) |
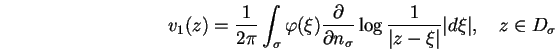 et
l'on a le résultat suivant.
et
l'on a le résultat suivant.
![]()
Il est important de souligner que le calcul de ![]() ne
nécessite pas une résolution systématique du problème direct pour
chaque
ne
nécessite pas une résolution systématique du problème direct pour
chaque ![]() car v0 n'est évaluée que sur
car v0 n'est évaluée que sur 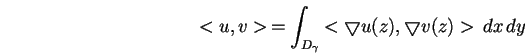 ,
et l'on
peut donc l'obtenir par l'opérateur de Poincaré-Steklov
,
et l'on
peut donc l'obtenir par l'opérateur de Poincaré-Steklov ![]() associé au domaine sain.
associé au domaine sain.
Les auteurs décrivent dans la dernière partie de l'article un moyen
numérique d'estimer si un segment ![]() est ``proche'' de la
fissure
est ``proche'' de la
fissure ![]() en calculant un coefficient
en calculant un coefficient
![]() qui
tend vers 1 lorsque le segment test s'approche de
qui
tend vers 1 lorsque le segment test s'approche de ![]() .
.
|
[Position de la fissure et d'un segment test]
[width=.35]plotBHP1.ps
[Topologie du domaine]
[width=.45]plotBHP2.ps
|
|
[Segments pour lesquels |