Bibliography

OT1 $\ll$ OT1 $\gg$ url urlprefix

1

M. Ablowitz et A. Fokas, Complex variables, introduction and applications, Cambridge Texts in Applied Mathematics (1997).

2

V. M. Adamjan, D. Z. Arov et M. G. Krein, properties of Schmidt pairs for a Hankel operator and the generalized Schur-Takagi problem, Math. USSR Sbornik 15, 31-73 (1971).

3

G. Alessandrini, determination of a crack from boundary measurements, Proc. Royal Soc. Edinb. 123A, no. 3, 497-516 (1993).

4

G. Alessandrini, E. Beretta et S. Vessella, linear cracks by boundary measurements - Lipschitz stability, SIAM J. Math. Anal. 27, no. 2, 361-375 (1996).

5

G. Alessandrini et E. DiBenedetto, 2-dimensional cracks in 3-dimensional bodies: Uniqueness and stability, Indiana Univ. Math. J. 46, no. 1, 1-82 (1997).

6

G. Alessandrini et A. D. Valenzuela, determination of multiple cracks by two measurements, SIAM J. Control Optimization 34, no. 3, 913-921 (1996).

7

J. W. Alexander, which map the interior of the unit circle upon simple regions, Ann. of Math. 17, 12-22 (1915).

8

J.-E. Andersson, rational approximation to Markov functions, J. of Approximation Theory 76, 219-232 (1994).

9

S. Andrieux et A. Ben Abda, of planar cracks by complete overdetermined data: inversion formulae, Inverse Problems 12, 553-563 (1996).

10

S. Andrieux, A. Ben Abda et M. Jaoua, the inverse emerging plane crack problem, Rapport de recherche 3012, INRIA (1996).

11

L. Baratchart, l'approximation rationnelle L² pour les systèmes dynamiques linéaires., Thèse de doctorat, Université de Nice, 1987.

12

L. Baratchart, and generic properties for L² approximants of linear systems, I.M.A. Journal of Math. Control and Identification 3, 89-101 (1986).

13

L. Baratchart, M. Cardelli et M. Olivi, and rational L² approximation : a gradient algorithm, Automatica 27, no. 2, 413-418 (1991).

14

L. Baratchart, R. Küstner, F. Mandréa et V. Totik, distribution via orthogonality, Rapport de recherche, INRIA, en préparation.

15

L. Baratchart, J. Leblond, F. Mandréa et E. B. Saff, can the meromorphic approximation help to solve some 2D inverse problems for the Laplacian?, Inverse Problems 15, 79-90 (1999).

16

L. Baratchart, J. Leblond et J. R. Partington, of Adamjan-Arov-Krein type on subsets of the circle and minimal norm extensions, Constructive Approximation 16, 333-357 (2000).

17

L. Baratchart, E. B. Saff et F. Wielonsky, criterion for uniqueness of a critical points in H² rational approximation, J. Analyse Mathématique 70, 225-266 (1996).

18

L. Baratchart et F. Seyfert, L^p analog to the AAK theory for 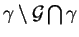$p \ge 2$, J. Functional Analysis (2000), a paraître.

19

L. Baratchart, H. Stahl et F. Wielonsky, uniqueness of best rational approximants of given degree to markov functions in l² of the circle, Constructive Approximation (2000), a paraître.

20

C. Baudelaire, et Idéal, Int. J. Mathematical Poetry 1, no. 3, 213-228 (1860).

21

H. G. W. Begehr, Complex analytic methods for partial differential equations, World Scientific (1994).

22

A. Ben Abda et M. Kallel, fast algorithms to recover line segment cracks by overspecified data, En préparation.

23

M. Brühl, M. Hanke et M. Pidcock, detection using electrostatic measurements, Prépublication, actuellement soumis dans Math. Modell. Numer. Anal.

24

K. Bryan et M. Vogelius, uniqueness result concerning the identification of a collection of cracks from finitely many electrostatic boundary measurements, SIAM J. Math. Anal. 23, no. 4, 950-958 (1992).

25

R. Douady et A. Douady, Algèbre et théories galoisiennes, tome 2, F. Nathan (1979).

26

P. L. Duren, Theory of H^p-spaces, Academic Press (1970).

27

A. R. Elcrat, V. Isakov et O. Neculoiu, finding a surface crack from boundary measurements, Inverse Problems 11, no. 2, 343-351 (1995).

28

K. Friedman et M. Vogelius, cracks by boundary measurements, Indiana Univ. Math. J. 38, no. 3, 527-556 (1989).

29

P. Fulcheri et M. Olivi, and matrix rational H² approximation: a gradient algorithm based on Schur analysis, Rapport de recherche 2520, INRIA (1995).

30

J. B. Garnett, Bounded Analytic Functions, Academic Press (1981).

31

J. Grimm, approximation of transfer functions in the Hyperion software, Rapport de recherche 4002, INRIA (2000).

32

P. Grisvard, Singularities in boudary value problems, Springer-Verlag (1992).

33

E. Hayashi, L. N. Trefethen et M. H. Gutknecht, CF Table, Constructive Approximation 6, 195-223 (1990).

34

P. Henrici, Applied and Computational Complex Analysis, tome 3, J. Wiley and Sons (1993).

35

S. Kakeya, zeros of a polynomial and its derivative, Tôhoku Math. J. 11, 5-16 (1917).

36

H. Kim et J. K. Seo, determination of a collection of a finite number of cracks from two boundary measurements, SIAM J. Math. Anal. 27, no. 5, 1336-1340 (1996).

37

J. L. Lions et E. Magenes, Problèmes aux limites non homogènes et applications, tome 1, Dunod (1968).

38

O. G. Parfenov, of the singular numbers of a Carleson operator, Math USSR Sbornik 59, no. 2, 497-514 (1988).

39

J. R. Partington, An Introduction to Hankel Operators, Cambridge University Press (1988).

40

J. R. Partington, identification and interpolation in 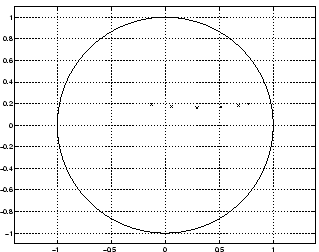${H}_\infty$, Int. J. Control 54, no. 5, 1281-1290 (1991).

41

V. V. Peller, operators and continuity properties of the operators of best approximation, Leningrad Math. J. 2, no. 1, 139-160 (1991).

42

V. V. Peller et S. V. Khrushchev, operators, best approximations, and stationary Gaussian processes, Russ. Math. Surv. 37, no. 1, 61-144 (1982).

43

C. Pommerenke, Boundary behaviour of conformal maps, Springer-Verlag (1991).

44

T. Ransford, Potential Theory in the Complex Plane, Cambridge University Press (1995).

45

L. Rondi, and stability for the determination of boundary defects by electrostatic measurements, Proc. Royal Soc. Edinb. A paraître.

46

W. Rudin, Real and Complex analysis, Mc Graw-Hill (1982).

47

E. B. Saff et V. Totik, Logarithmic Potentials with External Fields, tome 316 de Grundlehren der Math. Wissenschaften, Springer-Verlag (1997).

48

F. Santosa et M. Vogelius, computational algorithm to determine cracks from electrostatic boundary measurements, Int. J. Engng. Sci. 29, no. 8, 917-937 (1991).

49

G. Szegö, zu einem Satz von J.H. Grace über die Wurzeln algebraischer Gleichungen, Math. Z. 13, 28-55 (1922).

50

N. J. Young, An introduction to Hilbert space, Cambridge University Press (1988).