(See scanint for details of argument scanning).
This page contains the description of the following commands
\@m \@M \@M,
\m@ne,
\m@th,
\mag,
\mainmatter,
\@makeactive,
\makeatletter,
\makeatother,
\makebox,
\makeglossary,
\makeindex,
\MakeLowercase,
\@makeother,
\MakeUppercase,
\MakeTextUppercase,
\MakeTextLowercase,
\mapfrom,
\Mapfrom,
\mapsto,
\Mapsto,
\marginparpush,
\marginparsep,
\marginparwidth,
\mark,
\markboth,
\markright,
\marks,
\mathaccent,
\mathalpha,
\mathattribute,
\mathbb,
\mathbbm,
\mathbf,
\mathbin,
\mathbox,
\mathcal,
\mathchar,
\mathchardef,
\mathchoice,
\mathci,
\mathclose,
\mathcn,
\mathcnothing,
\mathcode,
\mathcsymbol,
\mathdollar,
\mathellipsis,
\mathfontproperty,
\mathfrak,
\mathgroup,
\mathinner,
\mathit,
\mathmi,
\mathmn,
\mathmo,
\mathnormal,
\mathop,
\mathopen,
\mathord,
\mathpalette,
\mathparagraph,
\mathpunct,
\mathrel,
\mathrm,
\mathsection,
\mathsf,
\maths\terling,
\mathstrut,
\mathsurround,
\mathtt,
\mathversion,
\max,
\maxdeadcycles,
\maxdepth,
\mbox,
\mdseries,
\meaning,
\measuredangle,
\medbreak,
\medskip,
\medskipamount,
\medmuskip,
\merge,
\message,
\mho,
\mid,
\middle,
\min,
\@minus,
\mkern,
\mml@font@bold,
\mml@font@boldfraktur,
\mml@font@bolditalic,
\mml@font@boldscript,
\mml@font@boldsansserif,
\mml@font@doublestruck,
\mml@font@fraktur,
\mml@font@italic,
\mml@font@monospace,
\mml@font@normal,
\mml@font@upright,
\mml@font@sansserif,
\mml@font@sanserifitalic,
\mml@font@sansserifbolditalic,
\mml@font@script,
\@mod,
\mmlmultiscripts,
\mmlnone,
\mmlprescripts,
\@mod,
\mod,
\models,
\moduleref,
\month,
moveleft,
moveright,
\mp,
mpfootnote,
\mskip,
\mu,
\muexpr,
\multicolumn,
\multimap,
\multi@math@label,
\multiply,
\multiput,
\multispan,
\muskip,
\muskipdef,
\mutoglue,
and environments
makeimage,
math,
minipage,
module,
modulex,
moreinfo,
motscle.
multline.
The commands \@m, \@M, \@MM are defined to be respectively 1000, 10000, and 20000 via \mathchardef. You should not use these commands as math characters, but as integer constants as in \sfcode`\.\@m (if the space-factor code of the dot is larger than 1000, then TeX will use wider spaces at the end of a sentence, mechanism not implemented in Tralics).
In standard LaTeX, \m@ne is \count22 (in Tralics, it is rather \count20). The counter is initialized to minus one, and LaTeX expects it to be constant. For instance, you may say
\ifnum \endlinechar<256 %
\ifnum \endlinechar>\m@ne
\catcode\endlinechar 10 %
\fi
\fi
(this changes the catcode of the endline char if is valid, hence between 0 and 255). Other example:
\gdef\dashbox {...
\ifodd\@dashcnt \@dashdim \z@
\advance\@dashcnt \@ne \divide\@dashcnt \tw@
\else
\divide\@dashdim \tw@ \divide\@dashcnt \tw@
\advance\@dashcnt \m@ne
...
Both plain.tex and latex.ltx have \def\m@th{\mathsurround\z@}. On the other hand, Tralics ignores the content of \mathsurround, hence defines \m@th as \relax.
When you say \mag=68,
then TeX will use this value (divided by 1000)
as magnification factor.
A magnification factor of 1200 increments every dimension by 20%,
unless expressed in terms of true units. The use of
\mag is discouraged by LaTeX.
It is ignored by Tralics.
(See scanint for details of argument scanning).
The three commands \frontmatter, \mainmatter, and \backmatter are defined by the book class in LaTeX. They set an internal switch to true or false; if the switch is false (outside main matter), chapters are not numbered: this affects the \chapter command (instead of `Chapter 0\par Introduction', there is only `Introduction'), the current mark (for headings), and what is printed on the TOC; moreover the chapter number is not increased (so that the first chapter of the main matter is numbered one). All commands use \cleardoublepage, \frontmatter uses \pagenumbering{roman}, while \mainmatter uses \pagenumbering{arabic}.
Since marks and the TOC is not handled by Tralics, the behavior is simpler. We maintain an internal switch so that \chapter becomes automatically \chapter*. On the other hand, the \mainmatter command terminates the current front matter (if any), hence terminates the current paragraph, section, chapter, etc, and starts a <mainmatter> element (it is terminated by the end of document or the \backmatter command). The name of the element will be foo if the configuration file contains xml_mainmatter_name="foo", the same holds for the two other elements.
After \@makeactive\A, the letter A becomes an active character. Instead of \A you can use any single-character command, or a character like in \@makeactive{B}.
After \@makeother\A, the letter A becomes a normal character. Instead of \A you can use any single-character command, or a character like in \@makeother{B}. By default, A is a letter, and changing the category code to non-letter is not recommended.
The effect of this command is to change the catcode of the at-sign to that of a letter, as in \catcode`@=11. We assume that this is true in most of the examples given in this documentation. Then \@foo is one token.
The effect of this command is to change the catcode of the at-sign to `other', as in \catcode`@=12. This is the default, so that \@foo is considered as \@ followed by foo. This is a way to protect against accidental use of private commands.
The normal syntax is \makebox[aa][bb]{cc} where the first optional argument is the width of the box, the second optional argument is the position (one character among l, r, c, or s). The translation is the same as \mbox{cc}, see description of \mbox below. In the case where optional arguments are given (and at least one is non-empty) the result is a <mbox> element with some attributes added.
The extended syntax is \makebox(a,b)[c]{text}, where the arguments are width, height and position. The position could be t (top) or bl (bottom left) or some variants. For simplicity, Tralics accepts any value. The dimensions are multiplied by \unitlength. In example E below, the first argument is 1,2 (everything between the opening parenthesis and the comma, with a pair of braces removed) so the width is 1,2\unitlength. Since the unit length defaults to one pt, it is 1.2pt. The translation gives only the value 1.2, not the unit. For another example, see \qbezier command.
A:\makebox{aa} B:\makebox[2pt]{bb} C:\makebox[33pt][l]{cc}
D\makebox (1.2,4,5)[q]{text}
E\count3=4 \makebox ({1,2},\count3)[p]{text}
F\def\FF{1,2}\makebox(\FF,\count3)[r]{text}
A:aa B:<mbox width='2.0pt'>bb</mbox> C:<mbox width='33.0pt' position='l'>cc</mbox> D<pic-framebox width='1.2' height='4.5' position='q'>text</pic-framebox> E<pic-framebox width='1.2' height='4' position='p'>text</pic-framebox> F<pic-framebox width='1.2' height='4' position='r'>text</pic-framebox>
This is a dummy environment: its content is translated normally.
This command is ignored: an index is made if the command \index is used. For details see see \index.
This command converts its argument to lower case. See below.
This command converts its argument to upper case.
Some special characters (defined via names) are also converted.
Before version 2.10.7, commands were not expanded. In the current version,
argument is fully expanded, and the \expandafter shown here
is not needed any more.
Example.
\def\List{{abcABC\oe\OE\o\O\ae\AE\dh\DH\dj\DJ\l\L\ng\NG\ss\SS\th\TH}}
\expandafter\MakeUppercase\List\\
\expandafter\MakeLowercase\List\\
Preview:
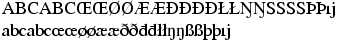
These two commands are provided by the textcase package. In the example that follows, everything is converted except the math formulas, arguments of \NoCaseChange, \label, \ref and \cite.
\def\SBU{Upper }
\def\SBL{Lower }
\def\SBM{Mixed }\ref{Cd1}\ref{Cd2}
a: \MakeTextUppercase{\SBU \NoCaseChange{MiXeD} \NoCaseChange{\SBM} \SBU }\\
b: \MakeTextUppercase{\SBU $\rm Bar \SBM$ \(Yy\), \ensuremath{Zz} \SBU}\\
c: \MakeTextUppercase{Text \cite{mathml2} and \cite[Page 12]{mathml2} \SBU}
d: \MakeTextUppercase{\ref{label-A} \label{Cd1} \SBU}\\
a: \MakeTextLowercase{\SBL \NoCaseChange{MiXeD} \NoCaseChange{\SBM} \SBL }\\
b: \MakeTextLowercase{\SBL $\rm Bar \SBM$ \(Yy\), \ensuremath{Zz} \SBL}\\
c: \MakeTextUppercase{Text \cite{mathml2} and \cite[Page 12]{mathml2} \SBL}
d: \MakeTextLowercase{\ref{label-A} \label{Cd2} \SBL}\\
<p><ref target='uid56'/><ref target='uid56'/> a: UPPER MiXeD Mixed UPPER</p> <p noindent='true'>b: UPPER <formula type='inline'> <math xmlns='http://www.w3.org/1998/Math/MathML'><mi> BarMixed </mi></math> </formula> <formula type='inline'> <math xmlns='http://www.w3.org/1998/Math/MathML'><mrow><mi>Y</mi><mi>y</mi></mrow> </math></formula>, <formula type='inline'> <math xmlns='http://www.w3.org/1998/Math/MathML'><mrow><mi>Z</mi><mi>z</mi> </mrow></math></formula> UPPER</p> <p noindent='true'>c: TEXT <cit><ref target='bid4'/></cit> AND <cit> <ref target='bid4'/></cit> UPPER d: <ref target='uid16'/> UPPER</p> <p noindent='true'>a: lower MiXeD Mixed lower</p> <p noindent='true'>b: lower <formula type='inline'> <math xmlns='http://www.w3.org/1998/Math/MathML'><mi> BarMixed </mi></math> </formula> <formula type='inline'> <math xmlns='http://www.w3.org/1998/Math/MathML'><mrow><mi>Y</mi><mi>y</mi> </mrow></math></formula>, <formula type='inline'> <math xmlns='http://www.w3.org/1998/Math/MathML'><mrow><mi>Z</mi><mi>z</mi> </mrow></math></formula> lower</p> <p noindent='true'>c: TEXT <cit><ref target='bid4'/></cit> AND <cit> <ref target='bid4'/></cit> LOWER d: <ref target='uid16'/> lower</p>
The \Mapsfrom command is valid only in math mode. It generates an arrow: <mo>⤆</mo> (Unicode U+2906, ⤆).
The \mapsfrom command is valid only in math mode. It generates an arrow: <mo>↤</mo> (Unicode U+21A4, ↤).
The \Mapsto command is valid only in math mode. It generates an arrow: <mo>⤇</mo> (Unicode U+2907, ⤇).
The \mapsto command is valid only in math mode. It generates an arrow: <mo>↦</mo> (Unicode U+21A6, ↦).
The normal behaviour of marginal notes is the outer margin (left margin in one side mode); the reverse of this behavior can be asked for. These two commands are ignored in Tralics.
These parameters control marginal notes, and define respectively the width of the margin par column, the distance between this column and the text, and the vertical distance between two notes. Unused in Tralics.
The \mark command takes one argument, and does nothing. In fact, the argument is expanded as in the commands \edef, \message etc., so that errors may be signaled. It is possible in TeX to refer to the first and last marks on a page, but since Tralics does not split the text into pages, this is useless.
This is an extension to \mark (see above) introduced by ε-TeX; an integer N is read, as well as an argument. Both arguments are ignored. See \splitbotmark for additional comments. One possible use is the following: you could use mark 0 for left pages and mark 1 for right pages, and use the following definitions, rather than complicated stuff.
\def\markboth#1#2{\marks0{#1}\marks1{#2}}
\def\markright#1{\marks1{#1}}
\def\leftmark{\botmark0 }
\def\rightmark{\firstmark1 }
The \markboth command takes two arguments, say A and B. It remembers the arguments in a variable, and calls \mark with {A}{B} as argument. There is a trick: the \mark command expands all tokens, and LaTeX manages to suppress (delay) expansion of \label \index \glossary. See also below.
The \markright command takes one argument, say B. It calls \mark with {A}{B} as argument, where A is the argument remembered by \markboth.
The idea is that A is the left mark (put on left pages), and B is the right mark (put on right pages). On the other hand, it is supposed that the left mark is a chapter mark, and the right mark is a section mark: when a new chapter is entered, both marks have to be changed, when a section is entered, only the section mark has to be changed.
In LaTeX, the internal command \@themark contains {A}{B}, after expansion (except for \label \index \glossary).
The babel package modifies this system: both the A-part and B-part contain a language switch, so that, when the mark is evaluated, it uses the right language.
In Tralics, we simplified the process, since the \mark command does nothing. The \@themark contains only the A-part. If you redefine \mark as \def\mark#1{\typeout{#1}}, then say \markboth{left}{right} \markright{Right}, you will see {left}{right} then {left}{Right}.
If you need a small (inline) math formula, you can enclose it in dollar signs (or any character of catcode 3), or say something like \(xx\) (this construct uses dollar characters of catcode 3), or \begin{math}xx\end{math}. You could even use \ensuremath. Example.
\begin{math}\alpha=\beta\end{math} and \(\gamma=\delta\) and $\phi=\psi$;
and \ensuremath{0\neq\infty}
This translates as
<p> <formula type='inline'> <math xmlns='http://www.w3.org/1998/Math/MathML'> <mrow><mi>α</mi><mo>=</mo><mi>β</mi></mrow></math> </formula> and <formula type='inline'> <math xmlns='http://www.w3.org/1998/Math/MathML'> <mrow><mi>γ</mi><mo>=</mo><mi>δ</mi></mrow></math> </formula> and <formula type='inline'> <math xmlns='http://www.w3.org/1998/Math/MathML'> <mrow><mi>ϕ</mi><mo>=</mo><mi>ψ</mi></mrow></math> </formula>; and <formula type='inline'> <math xmlns='http://www.w3.org/1998/Math/MathML'> <mrow><mn>0</mn><mo>≠</mo><mi>∞</mi></mrow></math></formula> </p>
Preview: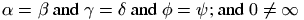 
.
In the case of \mathaccent <char> <field> TeX reads the 15-bit number <char> and converts it into c, f and a as it does with any \mathchar. Then it processes the field and appends a new Acc atom to the current list. The nucleus of this atom contains the specified field; the accent character in this atom contains (a,f). In Tralics, you get an error, a 15-bit number is read and ignored. (see scanint for details of number reading).
This command is currently ignored.
The \mathattribute command can only be used in math mode. It takes two arguments X and Y and adds X=Y to the attribute list of the last constructed XML element. (See also mathmo and \@nomathml). Example. The following command creates an operator that behaves like \min.
\providecommand\operatorname[1]{%
\mathmo{#1}%
\mathattribute{form}{prefix}%
\mathattribute{movablelimits}{true}%
}
\def\Dmin{\operatorname{dmin}}
$\min _xf(x) >\Dmin _xf(x)$.
Translation
<formula type='inline'> <math xmlns='http://www.w3.org/1998/Math/MathML'> <mrow> <msub><mo movablelimits='true' form='prefix'>min</mo> <mi>x</mi> </msub> <mrow><mi>f</mi><mo>(</mo><mi>x</mi><mo>)</mo><mo>></mo></mrow> <msub><mo movablelimits='true' form='prefix'>dmin</mo> <mi>x</mi> </msub> <mrow><mi>f</mi><mo>(</mo><mi>x</mi><mo>)</mo></mrow> </mrow> </math> </formula>
If your browser supports MathML, you can see the translation here
There are five other commands, that add an attribute pair to the current formula, the current math element, the current table, the current row, or the current cell; the next example shows how to add a tag attribute to the formula, a background attribute to the math, a color to the table, a mathvariant attribute to the first row, and to align the first cell of the last column to the left (default is right align).
\begin{align}
\formulaattribute{tag}{8-2-3}
\thismathattribute{background}{white}
\tableattribute{color}{black}
\rowattribute{mathvariant}{bold} x^2 + y^2+100 &= z^2 \\
\cellattribute{columnalign}{left} x^3 + y^3+1 &< z^3
\end{align}
Translation; for simplicity we have replaced some cell contents by XY2, XY3, Z2 and Z3
<formula id-text='mid1' id='uid1' textype='align' type='display' tag='8-2-3'>
<math xmlns='http://www.w3.org/1998/Math/MathML'
mode='display' background='white'>
<mtable displaystyle='true' color='black'>
<mtr mathvariant='bold'>
<mtd columnalign='right'><mrow> XY2</mrow></mtd>
<mtd columnalign='left'><mrow><mo>=</mo>Z2</mrow></mtd>
</mtr>
<mtr>
<mtd columnalign='left'><mrow>XY3</mrow></mtd>
<mtd columnalign='left'><mrow><mo><</mo>Z3</mrow></mtd>
</mtr>
</mtable>
</math>
</formula>
The \mathbb command can only be used in math mode.
It typesets the letters in its argument in a BlackBoard font.
(The bbm package provides an alternate black-board font, which can be used
via the \mathbbm command; Tralics make no difference).
For an example, see \mathtt.
The \mathbf command can only be used in math mode.
It typesets the letters in its argument in a boldface font.
For an example, see \mathtt.
The \mathbin declaration is valid only in math mode.
The item that follows (a character or a subformula in braces) is handled as a
binary operation.
For details see \mathord.
The \mathbox command can only be used in math mode.
It takes too arguments, A and B, constructs an element named A that contains
B; The second argument is evaluated inside a group. You can add attributes,
either by placing \mathattribute
after the command, or by putting the attribute pair between A and B.
See also mathmo.
The \mathcal command can only be used in math mode.
It typesets the letters in its argument in a calligraphic font.
For an example, see \mathtt.
In the case of \mathchar <char>,
TeX reads a 15-bit number
into c, f and a, by taking
respectively 3, 4 and 8 bits.
(see scanint for details of argument scanning.)
The quantity c contains a number between 0 and 7. If c=7, c is changed to 0, and in this case, if the current value of \fam is between 0 and 15, f is replaced by \fam (\fam is set to -1 at the beginning of \everymath and \everydisplay, thus the substitution of \fam for f will occur only if the user has explicitly changed \fam within the formula).
In Tralics, there are no classes, no families, no fonts. The \mathchar command is unimplemented (it nevertheless reads a 15-bit number). Note that TeX defines quantities like \itfam that assign symbolic names to families. LaTeX uses a different method.
If you say \mathchardef\foo8592, then you can use \foo instead of \mathchar8592. See above for how \mathchar can be used in TeX. In Tralics, \mathchardef behaves rather than \chardef (because characters are not restricted to 8 bits). As a consequence, the command \foo defined above produces, in math mode, the Unicode character U+2190: translation is <mi>←</mi>. This is the same character as \leftarrow, but uses <mi> instead of <mo>.
Note that, in some cases, \foo can be used as an integer. For instance, LaTeX defines \mathchardef\@MM=20000 (the \chardef command is used to define some integer constants less than 255, and \mathchardef for larger ones).
You can put the prefix \global before \mathchardef.
(see scanint for details of argument scanning.)
The \mathchoice declaration is valid only in math mode.
It reads four items. Only one is selected, depending on the mode.
See also the \frac command.
\def\mychoice{\mathchoice{a}{b}{c}{d}}
$$\mychoice = \frac{\mychoice}{\mychoice} =
1_{\mychoice\frac{\mychoice}{\mychoice}} =
2^ {\mychoice\frac{\mychoice}{\mychoice}}$$
oice}}$$
\begin{center}
$\mychoice = \frac{\mychoice}{\mychoice} =
1_{\mychoice\frac{\mychoice}{\mychoice}} =
2^ {\mychoice\frac{\mychoice}{\mychoice}}$
\end{center}
As you can see, exponents and indices are in mode 2, sub-exponents
and sub-indices in mode 3. The major mode is 0 (display style) or 1
(non-display style). The mode that follows 0 is 2 (except for fractions).
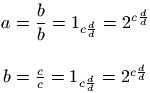
The \mathci command can only be used in math mode.
It typesets its argument as a <ci>
element. Translation of
$\mathci{xy}\mathrm{ab}\mathmi{cd}$ is
<ci>xy</ci> <mi> ab </mi>
<mi>cd</mi>.
See also mathmo.
The \mathclose declaration is valid only in math mode.
The item that follows (a character or a subformula in braces) is handled as a
closing atom.
For details see \mathord.
The \mathcn command can only be used in math mode.
It typesets its argument as a <cn> element.
Translation of \mathcn{12}=13=\mathmn{14} is
<cn>12></cn>
<mo>=</mo><mn>13></mn>
<mo>=</mo><mn>14</mn>.
See also mathmo.
The \mathcnothing command can only be used in math mode.
It typesets its argument as a character string element. For instance
$\mathcnothing{123}$ translates to 123.
In all other cases, digits are replaced by a <mn>
element.
See also mathmo.
When you say \mathcode13 12, you change the math code
of the character number 13 to the value 12.
The first integer must be a valid character code
(between 0 and 255 in TeX, 1023 in Tralics), and the second a valid math code (between 0 and 32767).
The math code is interpreted as a 3bit class code, plus a 4bit family code
and a 8bit character code.
This is unused by Tralics.
See scanint for details of how
numbers are read.
(see also \mathchar above).
The \mathcode of a character can be 32768. This means that the character should behave like an active character. In Plain TeX, as well as in LaTeX, this is used to make the prime character special. In Tralics, the prime character is naturally special in math mode. The mathcode table is empty.
The \mathcsymbol command can only be used in math mode.
It typesets its argument as a <csymbol> element.
Translation of $\mathcsymbol{xy}\sin\mathmo{cd}$ is
<csymbol>xy</csymbol><mo form='prefix'>sin</mo><mo>cd</mo>.
See also mathmo.
This command produces a dollar in math mode. It is the same as \$, thus can also be used outside math mode.
This command is equivalent to \ldots. Translation is <mo>...</mo>.
For each of the math fonts (see here some examples), there is a boolean that says whether a special Unicode character should be used, or an ASCII character with a mathvariant attribute. You can say \mathfrontproperty2=1, this sets the property of the mathfont number 2. Instead of 1, you can use any non-zero number (meaning true) or zero (meaning false). (See scanint for details of argument scanning). Instead of the integer 2, you can give a fontname, for instance a mathml font name like \mml@font@fraktur, or a TeX fontname like \mathbf.
If we have a math formula, and a current font F and a character c, the following happens: If c is neither a letter nor a digit, the translation of the character is a <mo>. If c is a digit, the result is <mn> element; if c is followed by some digits, then all these digits are put in the same element. Of course, in the case x^33, only one digit appears in the exponent. If the fontnumber F is zero (default font), then the translation is a <mi> element containing the character c; If the fontnumber F is one (obtained via \rm or similar) the translation is a <mi> element containing a space, the character c, all letters that follow, and a space. Finally, all letters are read, and the result is a <mi>. In the case where the boolean associated to the font is true, the content of the element is formed of the letters, and there is an attribute that depends on the font. If the boolean is false, then each character is replaced by the value found in a table; the value is an entity name (as 𝔞) or a character entity (as 𝗡), depending on options of the program; these values can be changed via the \setmathchar command. Note: the xmllatex trick is obsolete, it puts an unescaped anpersand in the XML tree.
\mathfontproperty2=3 $\mathbf{x}$
\the\mathfontproperty\mml@font@bold
\the\setmathchar\mathbf`x
\mathfontproperty\mathbf=0
\setmathchar\mathbf`x={\&\#x1d431;}
$\mathbf{x}$
% \setmathchar\mathbf`x={\xmllatex{\&\#x1dD431;}{}}
\setmathchar\mathbf`x={^^^^^1d431}
$\mathbf{x}$
Translation
<formula type='inline'>
<math xmlns='http://www.w3.org/1998/Math/MathML'>
<mi mathvariant='bold'>x</mi></math></formula>
1&#x1D431;
<formula type='inline'>
<math xmlns='http://www.w3.org/1998/Math/MathML'>
<mi>&#x1d431;</mi></math></formula>
<formula type='inline'>
<math xmlns='http://www.w3.org/1998/Math/MathML'>
<mi>𝐱</mi></math></formula>
The \mathfrak command can only be used in math mode. It typesets the letters in its argument in a fraktur font. The interesting part of the translation of $\mathfrak{Foo1}$ is
<mrow> <mi mathvariant='fraktur'>F</mi> <mi mathvariant='fraktur'>o</mi> <mi mathvariant='fraktur'>o</mi> <mn>1</mn> </mrow>
This command is defined as synonym for \fam in LaTeX. Not implemented in Tralics.
The \mathinner declaration is valid only in math mode.
The item that follows (a character or a subformula in braces) is handled as
an inner atom.
For details see \mathord.
The \mathit command can only be used in math mode.
It typesets the letters in its argument in a italic font.
For an example,
see \mathtt.
Note: commands of the form \@mathit were removed in
version 2.9.4.
The \mathmi command can only be used in math mode.
It typesets its argument as a <mi> element.
Translation of
$\mathci{xy}\mathrm{ab}\mathmi{cd}$ is
<ci>xy</ci> <mi> ab </mi>
<mi>cd</mi>.
See also mathmo.
The \mathmn command can only be used in math mode.
It typesets its argument as a <mn> element.
Translation of \mathcn{12}=13=\mathmn{14} is
<cn>12></cn>
<mo>=</mo><mn>13></mn>
<mo>=</mo><mn>14</mn>. This can be useful
if you want 1.2 to be considered as a number, rather than two
numbers separated by a dot operator.
See also mathmo.
The \mathmo command can only be used in math mode. It typesets its argument as a <mo> element. Only characters are allowed in the argument. Use \char`\$ if you a dollar character. Translation of $\mathcsymbol{xy}\sin\mathmo{cd}$ is <csymbol>xy</csymbol><mo form='prefix'>sin</mo><mo>cd</mo>.
[obsolete remark: Outside math mode, you can say \xmllatex{\&\#x125;}{}, and this allows you to access every Unicode character. It is invalid in math mode; you cannot use \mathchar"125 either. But you can use \mathmo{\&\#x125;}, the result is a <mo> element.] There is still the possibility to insert an unescaped amperesanr characater in the XML tree, by makei it of category code letter. In all other cases the translation of an ampersand character, \char`\& or \char`&, is an ampersand character.
Example.
%{\lccode`A=`&\lowercase{\xdef\amp{A}}} % Standard definition of \amp
$\mathmi{\amp\#x3B1;} \mathmn{\amp alpha;} \mathmo{\amp\#945;}$
$é\char`\é ^^^^abcd\char`\^^^^abcd\&\#\amp$
Translation
<formula type='inline'>
<math xmlns='http://www.w3.org/1998/Math/MathML'>
<mrow><mi>α</mi><mn>α</mn><mo>α</mo></mrow>
</math>
</formula>
<formula type='inline'>
<math xmlns='http://www.w3.org/1998/Math/MathML'>
<mrow><mi>é</mi><mi>é</mi><mi>ꯍ</mi><mi>ꯍ</mi>
<mo>&</mo><mo>#</mo><mo>&</mo>
</mrow>
</math>
</formula>
The commands \mathmn, \mathmi, \mathmo, \mathci, \mathcn, \mathcsymbol \mathcnothing and \mathbox take some optional arguments (in the case of \mathbox, there are given after the element name). If an odd number of optional arguments are given, the last one is discarded. If the remaining arguments are A1, V1, A2, V2, etc, then A1=V1, A2=V2, etc, is added to the attribute list of the element. This example shows how to produce a complex number using MathML content markup.
$\mathbox{cn}[type][complex-cartesian][id][id13]
{\mathcnothing{3}\mathbox{sep}{}\mathcnothing{4}}$
Translation
<formula type='inline'>
<math xmlns='http://www.w3.org/1998/Math/MathML'>
<cn id='id13' type='complex-cartesian'>3<sep/>4</cn>
</math>
</formula>
The following table was created by using \mathmo
on all Unicode characters between 2100 and 214B. Some glyphs are missing.
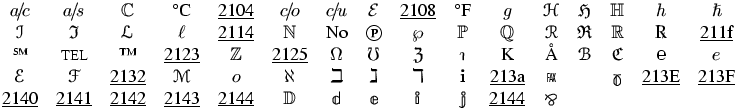
The \mathnormal command can only be used in math mode.
It typesets the letters in its argument in a normal font.
For an example, see \mathtt.
The \mathop declaration is valid only in math mode.
The item that follows (a character or a subformula in braces) is handled as a
large operator.
For details see \mathord.
The \mathopen declaration is valid only in math mode.
The item that follows (a character or a subformula in braces) is handled as
an opening atom.
For details see \mathord.
The \mathord declaration is valid only in math mode. The item that follows (a character or a subformula in braces) is handled as an ordinary atom.
Let's explain here how commands like \mathord work in TeX. The definite reference is appendix G to the TeXbook. There are thirteen kinds of atoms. Types Over, Under, Acc, Rad, Vcent are obtained by construction (overline, underline, adding an accent, constructing a radical, vertical centering). Types Ord, Op, Bin, Rel, Open, Close, Punct, Inner are obtained by defining characters via \mathchar, or commands like \mathord.
The table in the TeXbook page 170 explains how TeX puts spaces between atoms depending on their type. Tralics inserts no space in a formula (unless explicitly required by the user). TeX can insert a line break in a formula, after an explicit \penalty, or after a top-level atom of type relation or binary. Tralics does not format the formula, hence never inserts line breaks.
If you say \mathord\sum_x, then the sum sign is handled like an ordinary symbol, and the x is placed below it. In MathML it should be rendered by adding the movablelimits=false attribute.
If you say \mathop x _y, then x is considered as a large operator, like a \sum. In MathML it should be rendered by adding the movablelimits=true attribute.
Quoting Knuth The commands \displaylimits \limits \nolimits
are allowed only if the current list ends with an Op atom.
They modify a special field
in that Op atom specifying what convention should be used with respect to
limits. The normal value of that field is \displaylimits.
This means that the \limits command should be placed after an
operator and before the hat or underscore character.
We give here two example, a simple one and a more complicated one (definition from Plain).
\def\log{\mathop{\rm log}\nolimits
\def\overbrace#1{\mathop{\vbox{\m@th\ialign{##\crcr\noalign{\kern3\p@}
\downbracefill\crcr\noalign{\kern3\p@\nointerlineskip}
$\hfil\displaystyle{#1}\hfil$\crcr}}}\limits}
In MathML, a construction like a^b is rendered by a <msup> element. If a is an atom of type Op, and \limits is specified, then <mover> should be used instead. If \displaylimits is specified then the attribute movablelimits="true" should be added. In the current version of Tralics, nothing special is done. Thus \overbrace{xyz}^t could be wrongly translated. On the other hand, the following example:
$\sin(x) + \cos^2(x) $
is translated into
<formula type='inline'>
<math xmlns='http://www.w3.org/1998/Math/MathML'>
<mrow>
<mrow>
<mo form='prefix'>sin</mo><mo>(</mo><mi>x</mi><mo>)</mo>
</mrow>
<mo>+</mo>
<msup><mo form='prefix'>cos</mo><mn>2</mn></msup>
<mrow><mo>(</mo><mi>x</mi><mo>)</mo></mrow>
</mrow>
</math>
</formula>Preview: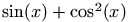 
If you say A\mathbin x B, then x is considered as a binary operator. If x is the first element in the list or is preceded by an atom of type Bin, Op, Rel, Open, Punct, or is followed by a Rel, Close, Punct, then Ord will be used instead; the same holds if it is the last element in the list. See TeXbook, Appendix G. These rules are needed by TeX in order to get the spacing right. In Tralics, nothing special is done, and we let the MathML renderer handle the spacing. However, Tralics adds some <mrow> elements in the math formula, and uses this information.
In Tralics, if you say \int f(a+b)=c+d, there is a complicated mechanism that understands that small parentheses should be used. The formula is split into pieces according to Bin and Rel operators. Here one piece would be b). Since this contains unmatched parentheses, the formula is split according to Rel operators, so that one piece will be \int f(a+b), and the size of the parentheses is unaffected by the other part.
If you say \int f\mathopen)a+b\mathclose(=c+d,
the spacing (and the size of the parentheses) should be the same as above,
because what follows f is an opening atom (a left parenthesis, or an object
declared as such). If an operator is declared Open or Close, Tralics should
perhaps add a attribute, either form="prefix" or
form="postfix" if this is not the default, and maybe also
fence=true. In any case, the example gives this
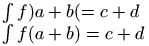
If you say a\mathpunct b c, then b behaves like a punctuation
in math mode, this means that there is space after it, but not before.
A possible translation would be to add a separator="true" attribute,
but according to the MathML recommendation linebreaking should be avoided
just before separators, but is acceptable just after them.
This means that a
comma has not the same meaning in TeX and in MathML. In the current version,
Tralics ignores the \mathpunct declaration.
If you say \mathinner a, then a is considered as a "delimited subformula", whatever this means. Tralics makes no difference between an Inner and an Ord atom. It ignores the \mathinner declaration.
According to Knuth, \bigl, \bigr, \bigm, \big all produce identical delimiters, the only difference between them is that they may lead to different spacing, because the result is Open, Close, Rel, or Ord. Here `big' can be replaced by big, Big, bigg, and Bigg. The nominal size are 8.5, 11.5, 14.5 and 17.5 times pt in plain TeX or \p@ in LaTeX. The size are 1.0, 1.5, 2. and 2.5 times some quantity X in amsmath; this quantity X being 1.2 times the total height and width of a special strutbox (hence is 12pt in ten-point document, 14.4pt in a twelve-point document, hence much larger). The definition of \big is is bit special: first a math formula is constructed, it contains \left, the argument of \big, an empty vbox of the desired size and \right. (this implies that \big{\relax(} is correct). The assignment \nulldelimiterspace=0pt is performed so that the width of \right. will be zero. The math formula is put in a hbox, and this box in a group. Consider: $\everyhbox{x}\everyvbox{y}\everymath{z}\big($. The math formula contains 'z' before the parenthesis, unless you load the amsmath package, which makes sure that the \everymath is empty. After the parenthesis, you will see 'y'; this is because the empty vbox is no more empty (note that the \vbox is underfull, and the math formula will produce an overfull \hbox). Finally, before the parenthesis, you will see 'x'.
The Tralics behavior is different. These command insrt special marker in the math list under construction. An attempt is made to match a bigl with a bigr; if this succeeds, the result is as if \left\right has been used. This does not always work. A good example is the following.
$\bigl[\frac{1}{a^2}\bigr[$
$\left[\frac{1}{b^2}\right[$
$[\frac{1}{x^2}[$
<formula type='inline'><math xmlns='http://www.w3.org/1998/Math/MathML'> <mfenced open='[' close='['><mfrac><mn>1</mn> <msup><mi>a</mi> <mn>2</mn> </msup></mfrac></mfenced></math></formula> <formula type='inline'><math xmlns='http://www.w3.org/1998/Math/MathML'> <mfenced open='[' close='['><mfrac><mn>1</mn> <msup><mi>b</mi> <mn>2</mn> </msup></mfrac></mfenced></math></formula> <formula type='inline'><math xmlns='http://www.w3.org/1998/Math/MathML'> <mrow><mrow><mo>[</mo></mrow><mfrac><mn>1</mn> <msup><mi>x</mi> <mn>2</mn> </msup></mfrac><mrow><mo>[</mo></mrow></mrow></math></formula>
Preview: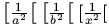 
Plain TeX has a macro called \mathpalette that is useful for \mathchoice constructions; `\mathpalette\a{xyz}' expands to the four-pronged array of choices `\mathchoice {\a\displaystyle {xyz}} ... {\a\scriptscriptstyle {xyz}}'. Thus the first argument to \mathpalette is a control sequence whose first argument is a style section. Appendix B contains several examples that show how \mathpalette can be applied (quote from the TeXbook, the command is implemented in the same way in Tralics, but not used).
This command is valid in math mode only. Its translation is <mo>¶</mo> (Unicode U+B6, ¶);
The \mathpunct declaration is valid only in math mode.
The item that follows (a character or a subformula in braces) is handled as
a punctuation atom.
For details see \mathord.
The \mathrel declaration is valid only in math mode.
The item that follows (a character or a subformula in braces) is handled as a
relation.
For details see \mathord.
This command is valid in math mode only. Its translation is <mo>˚</mo> (Unicode U+2DA, ˚).
The \mathrm command can only be used in math mode.
It typesets the letters in its argument in a Roman font.
For an example, see \mathtt.
This command is valid in math mode only. Its translation is <mo>§</mo> (Unicode U+A7, §);
The \mathsf command can only be used in math mode.
It typesets the letters in its argument in a sansserif font.
For an example, see \mathtt.
This command is an alias for \pounds It generates the pound sign £.
This command is identical to \strut. It produces an invisible element with non-zero dimensions.
When you say \mathsurround=5pt,
then TeX will put 5pt before and after every math formula.
LaTeX has the following definition
\def\m@th{\mathsurround\z@}.
This parameter is ignored by Tralics, and \m@th is a no-op.
(See scandimen for details of argument scanning).
The \mathtt command can only be used in math mode.
It typesets the letters in its argument in a typewriter font.
Implementation changed in Tralics 2.9.4. On one hand, the translation
of \mathbb{A} can be
<mi>𝔸</mi> (this is
the default), or <mi>𕴸</mi>
(if option -noententnames is selected) or
<mi mathvariant='doublestruck'>A</mi>
(if option -mathvariant is selected). Moreover, a single
<mi> is created for a sequence of letters using
the same font (in the case of \mathtt{x}\mathtt{y}, there are
two sequences of length one). Moreover, the current math version can be bold
or normal; if it is bold, then a bold version is selected for
\mathcal, \mathfrak, \mathit, and
\mathsf. In fact, \mathtt (and related font changes)
are replaced by commands like \mml@font@monospace (see description of these commands for further example).
Example:
\def\test#1#2{\mathtt{#1#2}\mathcal{#1}\mathbf{#1#2}\mathrm{#1#2}
\mathit{#1#2}\mathbb{#1}\mathsf{#1#2}\mathnormal{#1#2}}
\begin{equation}\begin{split}
\test Aa &\test Bb\\
\test Cc &\test Dd\\
\test Ee &\test Ff\\
\test Gg &\test Hh\\
\test Ii &\test Jj\\
\test Kk &\test Ll\\
\test Mm &\test Nn\\
\test Oo &\test Pp\\
\test Qq &\test Rr\\
\test Ss &\test Tt\\
\test Uu &\test Vv\\
\test Ww &\test Xx\\
\test Yy &\test Zz\\
\end{split}
\end{equation}
The XML result is shown here.
Preview:
The \mathversion command takes one argument and expands it using \csname, nasty errors may occur in some space cases. If the argument is bold then \@mathversion1\relax is executed, otherwise the number one is replaced by the number zero. This changes the value of the counter \@mathversion (in LaTeX, the command \math@version is set in this case). If the counter is one, then \mathcal, \mathfrak, \mathit, and \mathsf select a bold version.
The \max command is valid only in math mode. Its translation is
a math operator of the same name:
<mo form='prefix' movablelimits='true'>max</mo>.
For an example see the
\log command.
When you say \maxdeadcycles=71,
then TeX will use 71 for the maximum number of calls of
\output without a \shipout.
Tralics does not care about this.
(See scanint for details of argument scanning).
You can say \maxdepth=1.5in, as a result TeX
will make sure that the last line (box) of a page has a depth not exceeding
1.5in (by shifting it up if necessary). Ignored by Tralics.
(See scandimen for details of argument scanning).
This is the maximum length; it is 214pt or 16384pt, minus one sp
The \mbox command is a bit strange. In LaTeX, it is like \hbox{} but has hooks for colors and the like. In Tralics, like the case of \hbox{}, the argument is translated in a group. The result is put in a <mbox> element, unless in the following two cases. In the case of a math formula, a <mtext> element is generated (see example E below). In this case, the argument of the \mbox command should only contain characters and spaces. The <mbox> element is removed in the case where its content is formed only of text or a font change (in LaTeX, the box is used to inhibit hyphenation) or an image (the \mbox is useless in current LaTeX, perhaps, it was useful in version 2.09). Example
A:\mbox{aa}, B:\mbox{\it bb}, C:\mbox{\includegraphics{Logo-INRIA-couleur}}
D:\mbox{$a=y$}, E: $a=b\mbox{by definition}$.
This is the XML translation.
<p>A:aa, B:<hi rend='it'>bb</hi>, C:<figure file='Logo-INRIA-couleur'/> D:<mbox><formula type='inline'> <math xmlns='http://www.w3.org/1998/Math/MathML'> <mrow><mi>a</mi><mo>=</mo><mi>y</mi></mrow></math></formula></mbox>, E: <formula type='inline'><math xmlns='http://www.w3.org/1998/Math/MathML'> <mrow><mi>a</mi><mo>=</mo><mi>b</mi><mrow><mtext>by</mtext> <mspace width='0.5em'/><mtext>definition</mtext></mrow></mrow></math></formula>. </p>
The \mdseries command changes the series of the current font to
a medium (non-bold) one.
For an example of fonts, see \rm.
The \meaning command is like \show, but the expansion is a token list. All characters are all of catcode 12, except for spaces. Example.
\def\Bar#1#{#1} \meaning\Bar
\let\foo\par \meaning\foo
\renewcommand\foo[2][toto]{#1#2} \meaning\foo
\let\foo=1 \meaning\foo
\let\foo=\undef \meaning\foo
\meaning\bgroup
\catcode `\A=1 \meaning A
\catcode `\A=2 \meaning A
ok \catcode `\A=3 \meaning A
\catcode `\A=4 \meaning A
\catcode `\A=6 \meaning A
\catcode `\A=7 \meaning A
\catcode `\A=8 \meaning A
\expandafter \meaning \space
\catcode `\A=11 \meaning A
\catcode `\A=12 \meaning A
\catcode `\A=13 \meaning A
\def A{foo} \meaning A
This is the XML.
<p>macro:#1#->#1\par opt \long macro:toto#2->#1#2 the character 1undefinedbegin-group character {
</p><p>
begin-group character A
end-group character A
ok math shift character A
alignment tab character A
macro parameter character A
superscript character A
subscript character A
blank space the letter A
the character A
undefined
macro:->foo
</p>
The following code attempts to count the number of tokens in the result of \meaning\foo. The \lengthaux command is poorly written, in that it does not count spaces, so that the result is off by 5 (there are 53 tokens in the list).
\def\empty{}
\def\lengthof#1{\def\lengthres{0}\ifx#1\empty\else\count0=1
\lengthaux #1\relax\edef\lengthres{\the\count0 }\fi}
\def\lengthaux#1#2\relax{\ifx#2\empty\else\advance\count0 by1
\lengthaux #2\relax\fi}
\let\foo\par
\renewcommand\foo[2][toto]{#1#2}
\xdef\Bar{{\meaning\foo}}
\expandafter\lengthof\Bar\testeq\lengthres{48}
The idea of using \strip@prefix comes from the TeXbook, appendix D, paragraph 3.
\makeatletter
\def\strip@prefix#1>{}
\def\foo#1#2{OK OK}
\edef\Bar{\expandafter\strip@prefix\meaning\foo}
{\catcode `\O=12 \catcode `\K=12 \testeq\Bar{OK OK}}
The command \measuredangle is valid in math mode only. Its translation is <mo>∡</mo> (Unicode U+2221, ∡).
In Tralics, the \medbreak command is the same as \par. In LaTeX, it makes also sure that the space between the two paragraphs is at least \medskipamount, by calling \medskip if necessary; not implemented in Tralics.
The \medmuskip command is like the \thickmuskip command.
The \medskip command is like the \smallskip command. (see also the \vskip command).
This is defined by Tralics in the same way as in LaTeX, but is unused, see \smallskip
The command \merge is valid in math mode only. Its translation is <mo>&2A07;</mo> (Unicode U+2A07, ⨇).
The \message command reads a token list, expands it and prints the result on the terminal. Note that TeX prints a space or a newline before the message in some cases. This is not done by Tralics.
The \mho command is valid only in math mode. It generates a miscellaneous symbol: <mo>℧</mo> (Unicode U+2127, ℧). See description of the \ldots command.
The \mid command is valid only in math mode. It generates a relation symbol: <mo>∣</mo> (Unicode U+2223, ∣). See description of the \le command.
Not yet implemented.
The \min command is valid only in math mode. Its translation is a math operator of the same name <mo form='prefix' movablelimits='true'>min</mo>. For an example see the \log command.
You can say \begin{minipage}[pos][height][inner-pos]{width} text \end{minipage}. The [height] argument is ignored; the {width} specifies a dimension. The two optional arguments should The [pos] and [inner-pos] argument can b should be c, t or b, the [inner-pos] argument should be c, t, b, or s. No error is signaled, but invalid arguments are ignored.
When a minipage is started, \leavevmode is executed
(so that the minipage is inside a paragraph), and the current mode is set
to vertical mode (so that a new paragraph will be started inside the minipage).
The content is flushed left and right (unless you put a command like
\centering inside the minipage.)
Example:
\begin{center} xx
{ \begin{minipage}{2cm}abc\end{minipage} \par xx}
\end{center}
\begin{minipage}[t]{2cm}abc\end{minipage}
\begin{minipage}[b]{2cm}abc\end{minipage}
\begin{minipage}[c]{2cm}abc\end{minipage}
\begin{minipage}[c][xxx][s]{2cm}abc\end{minipage}
Translation:
<p rend='center'>xx</p> <p rend='center'><minipage width='56.9055pt'><p>abc</p></minipage></p> <p rend='center'>xx</p> <p><minipage pos='t' width='56.9055pt'><p>abc</p></minipage> <minipage pos='b' width='56.9055pt'><p>abc</p></minipage> <minipage pos='c' width='56.9055pt'><p>abc</p></minipage> <minipage inner-pos='s' pos='c' width='56.9055pt'><p>abc</p></minipage></p>
This command expands to minus. Do not modify it.
The \mkern command is valid only in math mode.
In the current version of Tralics, there is no difference
between \mkern2mu and \mskip2mu.
See \mskip.
The translation of $a\mkern2mub$ is
<math><mrow><mi>a</mi><mspace width='1.111pt'/><mi>b</mi></mrow></math>
There are 15 internal commands for fonts in math mode. They affect how letters are translated. If the font is normal, translation is of the form <mi>a</mi>, if the font is upright, translation is <mi> a </mi>; otherwise the result depends on some options. Here is a little test.
\def\F#1{\csname mml@font@#1\endcsname}
\def\A{ab+2c=DE}
$ \F{normal} \A \F{upright} \A \F{bold} \A \F{italic} \A
\F{bolditalic} \A \F{script} \A \F{boldscript} \A \F{fraktur} \A
\F{doublestruck} \A \F{boldfraktur} \A \F{sansserif} \A \F{boldsansserif} \A
\F{sansserifitalic} \A \F{sansserifbolditalic} \A \F{monospace} \A $
Normal case. Entity names are used whenever possible.
<formula type='inline'>
<math xmlns='http://www.w3.org/1998/Math/MathML'>
<mrow>
<mi>a</mi> <mi>b</mi> <mo>+</mo> <mn>2</mn> <mi>c</mi> <mo>=</mo>
<mi>D</mi> <mi>E</mi>
<mi> ab </mi> <mo>+</mo> <mn>2</mn> <mi> c </mi> <mo>=</mo>
<mi> DE </mi>
<mi>𝐚𝐛</mi><mo>+</mo> <mn>2</mn>
<mi>𝐜</mi> <mo>=</mo> <mi>𝐃𝐄</mi>
<mi>𝑎𝑏</mi> <mo>+</mo> <mn>2</mn>
<mi>𝑐</mi> <mo>=</mo> <mi>𝐷𝐸</mi>
<mi>𝒂𝒃</mi> <mo>+</mo> <mn>2</mn>
<mi>𝒄</mi> <mo>=</mo> <mi>𝑫𝑬</mi>
<mi>𝒶𝒷</mi> <mo>+</mo> <mn>2</mn>
<mi>𝒸</mi> <mo>=</mo> <mi>𝒟ℰ</mi>
<mi>𝓪𝓫</mi> <mo>+</mo> <mn>2</mn>
<mi>𝓬</mi> <mo>=</mo><mi>𝓓𝓔</mi>
<mi>𝔞𝔟</mi><mo>+</mo> <mn>2</mn>
<mi>𝔠</mi> <mo>=</mo> <mi>𝔇𝔈</mi>
<mi>𝕒𝕓</mi> <mo>+</mo> <mn>2</mn>
<mi>𝕔</mi> <mo>=</mo> <mi>𝔻𝔼</mi>
<mi>𝖆𝖇</mi> <mo>+</mo> <mn>2</mn>
<mi>𝖈</mi> <mo>=</mo> <mi>𝕯𝕰</mi>
<mi>𝖺𝖻</mi> <mo>+</mo> <mn>2</mn>
<mi>𝖼</mi><mo>=</mo> <mi>𝖣𝖤</mi>
<mi>𝗮𝗯</mi><mo>+</mo> <mn>2</mn>
<mi>𝗰</mi><mo>=</mo> <mi>𝗗𝗘</mi>
<mi>𝘢𝘣</mi><mo>+</mo><mn>2</mn>
<mi>𝘤</mi><mo>=</mo> <mi>𝘋𝘌</mi>
<mi>𝙖𝙗</mi> <mo>+</mo> <mn>2</mn>
<mi>𝙘</mi><mo>=</mo> <mi>𝘿𝙀</mi>
<mi>𝚊𝚋</mi> <mo>+</mo> <mn>2</mn>
<mi>𝚌</mi> <mo>=</mo> <mi>𝙳𝙴</mi>
</mrow>
</math>
</formula>
Case where Tralics is called with option -noentnames. No entity names are used.
<formula type='inline'>
<math xmlns='http://www.w3.org/1998/Math/MathML'>
<mrow>
<mi>a</mi> <mi>b</mi> <mo>+</mo> <mn>2</mn> <mi>c</mi> <mo>=</mo>
<mi>D</mi> <mi>E</mi> <mi> ab </mi> <mo>+</mo> <mn>2</mn>
<mi> c </mi> <mo>=</mo> <mi> DE </mi>
<mi>𝐚𝐛</mi> <mo>+</mo> <mn>2</mn>
<mi>𝐜</mi> <mo>=</mo> <mi>𝐃𝐄</mi>
<mi>𝑎𝑏</mi> <mo>+</mo> <mn>2</mn>
<mi>𝑐</mi> <mo>=</mo> <mi>𝐷𝐸</mi>
<mi>𝒂𝒃</mi> <mo>+</mo> <mn>2</mn>
<mi>𝒄</mi> <mo>=</mo> <mi>𝑫𝑬</mi>
<mi>𝒶𝒷</mi> <mo>+</mo> <mn>2</mn>
<mi>𝒸</mi> <mo>=</mo> <mi>𝒟ℰ</mi>
<mi>𝓪𝓫</mi> <mo>+</mo> <mn>2</mn>
<mi>𝓬</mi> <mo>=</mo> <mi>𝓓𝓔</mi>
<mi>𝔞𝔟</mi> <mo>+</mo> <mn>2</mn>
<mi>𝔠</mi> <mo>=</mo> <mi>𝔇𝔈</mi>
<mi>𝕒𝕓</mi> <mo>+</mo> <mn>2</mn>
<mi>𝕔</mi> <mo>=</mo> <mi>𝔻𝔼</mi>
<mi>𝖆𝖇</mi> <mo>+</mo> <mn>2</mn>
<mi>𝖈</mi> <mo>=</mo> <mi>𝕯𝕰</mi>
<mi>𝖺𝖻</mi> <mo>+</mo> <mn>2</mn>
<mi>𝖼</mi> <mo>=</mo> <mi>𝖣𝖤</mi>
<mi>𝗮𝗯</mi> <mo>+</mo> <mn>2</mn>
<mi>𝗰</mi> <mo>=</mo> <mi>𝗗𝗘</mi>
<mi>𝘢𝘣</mi> <mo>+</mo> <mn>2</mn>
<mi>𝘤</mi> <mo>=</mo> <mi>𝘋𝘌</mi>
<mi>𝙖𝙗</mi> <mo>+</mo> <mn>2</mn>
<mi>𝙘</mi> <mo>=</mo> <mi>𝘿𝙀</mi>
<mi>𝚊𝚋</mi> <mo>+</mo> <mn>2</mn>
<mi>𝚌</mi> <mo>=</mo> <mi>𝙳𝙴</mi>
</mrow>
</math>
</formula>
It is possible to generate a mathvariant attribute; this can be achieved by calling Tralics with option -mathvariant. You can also use the \mathfontproperty counter.
<formula type='inline'>
<math xmlns='http://www.w3.org/1998/Math/MathML'>
<mrow>
<mi>a</mi> <mi>b</mi> <mo>+</mo> <mn>2</mn> <mi>c</mi>
<mo>=</mo> <mi>D</mi> <mi>E</mi>
<mi> ab </mi> <mo>+</mo> <mn>2</mn> <mi> c </mi>
<mo>=</mo> <mi> DE </mi>
<mi mathvariant='bold'>ab</mi> <mo>+</mo> <mn>2</mn>
<mi mathvariant='bold'>c</mi> <mo>=</mo> <mi mathvariant='bold'>DE</mi>
<mi mathvariant='italic'>ab</mi> <mo>+</mo> <mn>2</mn>
<mi mathvariant='italic'>c</mi> <mo>=</mo> <mi mathvariant='italic'>DE</mi>
<mi mathvariant='bold-italic'>ab</mi> <mo>+</mo> <mn>2</mn>
<mi mathvariant='bold-italic'>c</mi> <mo>=</mo> <mi mathvariant='bold-italic'>DE</mi>
<mi mathvariant='script'>ab</mi> <mo>+</mo> <mn>2</mn>
<mi mathvariant='script'>c</mi> <mo>=</mo> <mi mathvariant='script'>DE</mi>
<mi mathvariant='bold-script'>ab</mi> <mo>+</mo> <mn>2</mn>
<mi mathvariant='bold-script'>c</mi> <mo>=</mo> <mi mathvariant='bold-script'>DE</mi>
<mi mathvariant='fraktur'>ab</mi> <mo>+</mo> <mn>2</mn>
<mi mathvariant='fraktur'>c</mi> <mo>=</mo> <mi mathvariant='fraktur'>DE</mi>
<mi mathvariant='double-struck'>ab</mi> <mo>+</mo> <mn>2</mn>
<mi mathvariant='double-struck'>c</mi> <mo>=</mo> <mi mathvariant='double-struck'>DE</mi>
<mi mathvariant='bold-fraktur'>ab</mi> <mo>+</mo> <mn>2</mn>
<mi mathvariant='bold-fraktur'>c</mi> <mo>=</mo> <mi mathvariant='bold-fraktur'>DE</mi>
<mi mathvariant='sans-serif'>ab</mi> <mo>+</mo> <mn>2</mn>
<mi mathvariant='sans-serif'>c</mi> <mo>=</mo> <mi mathvariant='sans-serif'>DE</mi>
<mi mathvariant='bold-sans-serif'>ab</mi> <mo>+</mo> <mn>2</mn>
<mi mathvariant='bold-sans-serif'>c</mi> <mo>=</mo> <mi mathvariant='bold-sans-serif'>DE</mi>
<mi mathvariant='sans-serif-italic'>ab</mi> <mo>+</mo> <mn>2</mn>
<mi mathvariant='sans-serif-italic'>c</mi> <mo>=</mo> <mi mathvariant='sans-serif-italic'>DE</mi>
<mi mathvariant='sans-serif-bold-italic'>ab</mi> <mo>+</mo> <mn>2</mn>
<mi mathvariant='sans-serif-bold-italic'>c</mi> <mo>=</mo>
<mi mathvariant='sans-serif-bold-italic'>DE</mi>
<mi mathvariant='monospace'>ab</mi> <mo>+</mo> <mn>2</mn>
<mi mathvariant='monospace'>c</mi> <mo>=</mo> <mi mathvariant='monospace'>DE</mi>
</mrow>
</math>
</formula>
Normally, you do not use these low-level commands. You say something like \mathsf{x} and you get a sans-serif letter x. If the current math version is bold, you will get a bold-sans-serif letter. Here is an example.
\mathversion{normal}
$Xx\mathcal{Cal}\mathrm{Rm}\mathbf{Bf}\mathsf{Sf}\mathtt{Tt}\mathnormal{No}
\mathit{It}\mathfrak{Fr}$
\mathversion{bold}
$Xx\mathcal{Cal}\mathrm{Rm}\mathbf{Bf}\mathsf{Sf}\mathtt{Tt}\mathnormal{No}
\mathit{It}\mathfrak{Fr}$
Translation, using option -mathvariant
<formula type='inline'>
<math xmlns='http://www.w3.org/1998/Math/MathML'>
<mrow>
<mi>X</mi><mi>x</mi>
<mi mathvariant='script'>Cal</mi>
<mi> Rm </mi>
<mi mathvariant='bold'>Bf</mi>
<mi mathvariant='sans-serif'>Sf</mi>
<mi mathvariant='monospace'>Tt</mi>
<mi>N</mi><mi>o</mi>
<mi mathvariant='italic'>It</mi>
<mi mathvariant='fraktur'>Fr</mi>
</mrow>
</math>
</formula>
<formula type='inline'>
<math xmlns='http://www.w3.org/1998/Math/MathML'>
<mrow>
<mi>X</mi><mi>x</mi>
<mi mathvariant='bold-script'>Cal</mi>
<mi> Rm </mi>
<mi mathvariant='bold'>Bf</mi>
<mi mathvariant='bold-sans-serif'>Sf</mi>
<mi mathvariant='monospace'>Tt</mi>
<mi>N</mi><mi>o</mi>
<mi mathvariant='bold-italic'>It</mi>
<mi mathvariant='bold-fraktur'>Fr</mi>
</mrow>
</math>
</formula>
Like \sin, but produces `mod'.
There is no difference between a\mod b and a~\@mod\;b. See also \bmod.
The \models command is valid only in math mode. It generates a relation symbol: <mo>⊧</mo> (Unicode U+22A7, ⊧). See description of the \le command.
This environment is defined for the RAWEB. It takes one optional argument (the topic), followed by three mandatory arguments: symbolic section name, module name, and module title. Example: \begin{module}[3]{}{appAI}{Static Analysis}. The section name must be one of those defined by the configuration file; it can be left empty if identical to the previous one. The equivalent of a \section command is automatically inserted between two modules of different sections. Since module behaves like a \subsection, subdivisions use \subsubsection commands. Translation may be <module id='uid19'><head>Static Analysis</head>....
Note. The semantics has changed in 2007, read carefully (See Old module definition). The topic argument is not used any more. Modules are no more re-ordered. The title of a module cannot be empty (except for the first one). The configuration file defines the valid sections as follows:
section_vals = "composition/presentation/fondements/domaine/logiciels/" section_vals = "+resultats/contrats/international/diffusion/"
or
fullsection_vals = "/composition/Team/presentation/Overall Objectives/\
fondements/Scientific Foundations/domaine/Application Domains/\
logiciels/Software/resultats/New Results/\
contrats/Contracts and Grants with Industry/\
international/Other Grants and Activities/diffusion/Dissemination"
The first syntax is used before 2007; since then full section names are given (the section title has beem moved from the DTD to the configuration file). The LaTeX source is unaffected by this change: the first module should be in the composition section, the second in the presentation, after that fondements, domain, etc, up to diffusion should be used.
This command is defined in the ra.plt style file with three arguments as \moduleref{p}{s}{a}, the expansion being \ref{mod:a}.
There is an option to the package that changes the syntax (for compatibility reasons). You can say \moduleref[y]{p}{s}{a}. The purpose is to make a reference to a module for the project-team p, section s, module a, for year y (the default value is current year). This command was never really implemented. It is an error if the [y] argument is given, and does not correspond to the current year. Otherwise, the [y] and {p} arguments are ignored. If {a} is empty, a reference is made to section:s, otherwise to mod:a. These labels are defined automatically for the RAWEB case.
When you say \month=905, you put 905 in the \month
counter, but nothing special happens. This counter is initially set
to the current month. So that
\the\month may be translated as 4 on the seventh of April 2004.
(See scanint for details of argument scanning).
(See \time for an example.)
The moreinfo environment puts its content in a <moreinfo> element. Note that a new paragraph is started inside the <moreinfo> element.
\begin{moreinfo}additional information\end{moreinfo}
Translation
<moreinfo><p>additional information</p></moreinfo>
The motscle environment is designed for keywords. Example.
\begin{motscle}
latex, xml, translator.
\end{motscle}
The translation is the following:
<keywords> <term>latex</term> <term>xml</term> <term>translator</term> </keywords>
If the configuration file contains the following lines
xml_keywords_name = "Keywords" xml_term_name = "Term"
then the result of the translation will be:
<Keywords> <Term>latex</Term> <Term>xml</Term> <Term>translator</Term> </Keywords>
This command reads a dimen and a box. The new box that is appended to the vertical list is shifted left by the specified amount. The dimension is ignored by Tralics
When TeX sees a box in vertical mode, and the box is not empty, it appends interline glue to the vertical list, then the box, then vertical material that migrates out of the new box (if this is a hbox). After that the \prevdepth is set to the new box depth, and TeX exercises the page builder.
Note that Tralics has no notion of `interline glue', boxes have no depth, no page builder has to be exercised. As a consequence \prevdepth is always zero.
You can't use `\moveleft' in horizontal mode (end of chapter 25 of the TeXbook).
There is a command \moveright that is similar.
There are two commands \lower and \raise that do not
work in vertical mode. The syntax is the same, the box is shifted up or
down by the specified amount. In math mode, a non-empty box
becomes an Ord atom (this does not work in Tralics). In horizontal
mode, an non-empty box is appended to the current list, and the
\spacefactor is set to 1000. In Tralics, the spacefactor
is not set.
(see scandimen for how dimensions are
read)
Like \moveleft above, but the box is shifted right.
The \mp command is valid only in math mode. It generates a binary operator (minus over plus): <mo>∓</mo> (Unicode U+2213, ∓). See description of the \pm command.
The \mskip command is valid only in math mode. Translation of $a\mskip 3.4mu plus 2fillb$, is <mspace width='1.88889pt'/>, since 18mu=10pt, and 3.4mu=17/9pt. Before version 2.13, the result was different, and we show here the transcript file associated to the formula:
{math shift character}
+stack: level + 2 for math
<!-- this shows how the skip is scanned -->
+scanint for \mskip->3
+scandimen for \mskip ->3.4pt
+scanint for \mskip->2
+scandimen for \mskip ->2.0pt
{scanglue 3.4pt plus 2.0fill}<!-- result of the skip -->
+stack: level + 3 for math<!-- brace for argument of \hspace -->
+stack: level - 3 for math
+stack: level - 2 for math
<!-- This is the formula to be interpreted -->
Math: $a\mskip (Changed to)\hspace {3.4pt}b$
<!-- this shows how \hspace scans its argument-->
+scanint for \hspace->3
+scandimen for \hspace ->3.4pt
{scanglue 3.4pt}<!-- The glue put in the formula -->
This is the transcript file for the current version
{math shift character}
{reassigning \@curmathfont=0}
+stack: level + 2 for math entered on line 9
+scanint for \mskip->3
+scandimen for \mskip->3.4mu
+scanint for \mskip->2
+scandimen for \mskip->2.0mu% unit is fill, display is wrong
{scanglue 3.4mu plus 2.0fill\relax }% This is the correct value of the glue
+stack: level - 2 for math from line 9
Math: $a\mskip b$
The \mu command is valid only in math mode. It generates a Greek letter: <mi>μ</mi> (Unicode U+3BC, μ). See description of the \alpha command.
This is a ε-TeX extension that read some muglue See \numexpr for details.
The \multicolumn should be used only in an array. It takes
three arguments A, B and C. The first argument is the number of columns
the cell spans, the second argument is the horizontal position (centered,
etc), and the third argument is the content of the cell.
For more information, see description of arrays.
In the example below, the table has two columns.
The first row has three cells, the second row spans
over 15 columns.
\begin{tabular}{cc}
a&b&c\\
\multicolumn{14}{l}{s}&e
\end{tabular}
<table rend='inline'> <row><cell halign='center'>a</cell><cell halign='center'>b</cell><cell>c</cell></row> <row><cell cols='14' halign='left'>s</cell><cell>e</cell></row></table>
The \multimap command is valid only in math mode. It generates <mi>⊸</mi> (Unicode U+22B8, ⊸).
There is a special counter \multi@math@label, whose value is normally zero; it is set to 1, when Tralics is called with the option -multi_math_label. Consider the following example.
\def\theequation{\thesection.\arabic{equation}}
\begin{equation}e=mc^2\label{x}\end{equation} \eqref{x}
\begin{equation}e=mc^2\tag{EQ}\label{y}\end{equation} \eqref{y}
The translation of the second line is given below. The main object
is a <formula> element, that has some
attributes: one that says that it should be typeset set in display
math mode (note that the math element has the same attribute), one
that says that is an equation
(this is the name of the TeX
environment); it has a unique id (uid1),
that is the target of the <ref>
element constructed by the \eqref command; there is
finally a id-text attribute, whose value is
the current label. This is some quantity that depends on the
context (we assume here that the formula is in the first section,
so that outside the formulas, the current label is the section
number, namely 1). In the formula, it is the value generated
by \refstepcounter{equation}. Since \p@equation
is undefined, it is the value of \theequation>. The
translation of the second equation is similar. The effect of the \tag
command is just to insert \qquad\mathrm{(EQ)} to the
right of the equation. This produces two additional lines, shown below.
One could say \tagasattribute; this has as effect
to insert tag='(EQ)' as attribute pair to
the main element. See \tag for details.
<formula id-text='1.1' id='uid1' textype='equation' type='display'>
<math mode='display' xmlns='http://www.w3.org/1998/Math/MathML'>
<mrow>
<mi>e</mi>
<mo>=</mo>
<mi>m</mi>
<msup><mi>c</mi> <mn>2</mn> </msup>
</mrow>
</math>
</formula>
<p noindent='true'>(<ref target='uid1'/>)</p>
...
<mspace width='2.em'/>
<mrow><mo>(</mo><mi> EQ </mi><mo>)</mo></mrow>
...
The following example is wrongly translated by Tralics. This
produces a set of two equations with an alignment point. The
<math> contains a table, with two
columns, the first is right-aligned, the second is left-aligned. In
principle each row is numbered. The value of the equation counter
is 3 (note that LaTeX decrements the equation counter whenever it
sees \tag or \notag, but not Tralics).
In this example, the equation counter is incremented one, but the
current label is defined locally in the first cell of the
table, hence lost. So the formula has
attributes id-text='1' id='uid4'. The
expectation is that \ref{a} and \ref{b}
point to the first and second row, and that the printed value
is the number of the equation and foo
respectively. Here,
by printed value, we mean some text that can be used in
a translation of the reference into HTML or Pdf as content of the
anchor; for us this is the id-text
associated to the id. It happens that the
first label points to the formula, and the second provokes an
error: Label will be lost: b.
\begin{align}
a&b \label{a} \\
c&d \tag{foo}\label{b}
\end{align}
Let's consider what happens when the counter \multi@math@label is non-zero, or the option -multi_math_label has been used. (we assume that the value of the equation counter is 4). The translation is exactly as above, except for some environments like align. These environments have a starred version, wich is unnumbered; in this case, \label, and \tag should not be used. One each row, there should be at most one label, at most one tag (otherwise, you will get an error message of the form Multiple \tag vv on row 3 of the formula or Multiple \abel uu on row 3 of the formula). The command \notag is interpreted as: do not increment the equation counter. It is ignored if either a tag or a label is given. If no tag is given, and either there is a label or \notag is omitted, then the equation counter is incremented; this will create a current label (in the example, it will be 1.5) which is memorized (Tralics behaves as if it had seen \tag{1.5}). If a tag is present, it will add two attribute pairs (for instance id-text='1.5' id='uid5') to the current row; if moreover a label is present, this will become the anchor of the label.
<formula textype='align' type='display'>
<math mode='display' xmlns='http://www.w3.org/1998/Math/MathML'>
<mtable displaystyle='true'>
<mtr id-text='1.5' id='uid5'>
<mtd columnalign='right'><mi>a</mi></mtd>
<mtd columnalign='left'><mi>b</mi></mtd>
</mtr>
<mtr id-text='foo' id='uid6'>
<mtd columnalign='right'><mi>c</mi></mtd>
<mtd columnalign='left'><mi>d</mi></mtd>
</mtr>
</mtable>
</math>
</formula>
Consider now the following example (LaTeX Companion, 8-2-25). There are 8 rows; the equation number is incremented for rows 1, 6, and 8. The second equation has no tag. Equations 3 and 4 have the same tag, which is a star in math mode; in particular, a \ref to one of these equations typesets the same as $*$; the equation number is enclosed in parentheses, except for a starred version of \tag. In Tralics you do not see the parentheses, so that there is no difference between \tag and \tag*. Moreover, the dollar signs are ignored (arbitrary objects can be used in LaTeX, but a character string is required in Tralics). Consider now row 5. When the \tag is evaluated, the XML element corresponding to the first row is not yet constructed, \label{eq:A1} is not yet evaluated, and \ref translates to an empty <ref> element; the attribute pair target='uid9' is added at the very end of the job (in some cases, this could be done earlier). We are in trouble: when Tralics converts the argument of \tag into a string, there is no way to modify the string by inserting later on the value 1.8 of the attribute id-text of the element whose id is the target so created (LaTeX solves the problem by storing information in auxiliary files, and the file has to be compiled at least twice). Note that the hyperref packages creates an anchor for each label. A symbolic reference of the anchor is stored in the auxiliary file. It could be equation.1.4 or AMS.11; there is a hyperlink of the \ref part of the \tag to the first equation. For this reason \ref is disabled while evaluation the tag. However, when line 8 is reached, \theequation produces the correct result.
\begin{align}
x^2+y^2 &= z^2 \label{eq:A1} \\
x^3+y^3 &= z^3 \notag \\
x^4+y^4 &= r^4 \tag{$*$} \\
x^5+y^5 &= r^5 \tag*{$*$} \\
x^6+y^6 &= r^6 \tag{\ref{eq:A1}$'$} \\
A_1 &= N_0 (\lambda ; \Omega')
- \phi ( \lambda ; \Omega') \\
A_2 &= \phi (\lambda ; \Omega')
\, \phi (\lambda ; \Omega)
\tag*{ALSO (\theequation)} \\
A_3 &= \mathcal{N} (\lambda ; \omega)
\end{align}
Translation. In order to reduce space, we replaced cells by locations of the form R3C2 (row 3, column 2).
<formula textype='align' type='display'>
<math mode='display' xmlns='http://www.w3.org/1998/Math/MathML'>
<mtable displaystyle='true'>
<mtr id-text='1.8' id='uid9'> R1C1 R1C2</mtr>
<mtr> R2C1 R2C2 </mtr>
<mtr id-text='*' id='uid10'> R3C1 R3C2 </mtr>
<mtr id-text='*' id='uid11'>R4C1 R4C2</mtr>
<mtr id-text='eq:A1'' id='uid12'>R5C1 R5C2</mtr>
<mtr id-text='1.9' id='uid13'> R6C1 R6C2</mtr>
<mtr id-text='ALSO (1.9)' id='uid14'> R7C1 R7C2</mtr>
<mtr id-text='1.10' id='uid15'> R8C1 R8C2</mtr>
</mtable>
</math>
</formula>
Note: Assume that you use the options -nomathml or -dualmath, or modify the value of the counter \@nomathml. In such a case, Tralics constructs a variant, a <texmath> object. This can be output as part of the <formula> or may replace it. For instance, the translation of the first equation could be <texmath id-text='1.1' id='uid1' textype='equation' type='display'>e=mc^2</texmath>; the translation of the second equation is similar, but the content is now e=mc^2\qquad \mathrm {(EQ)}. In the case of the third equation, if \multi@math@label is non-zero, the translation will be <texmath textype='align' type='display'> a&b \\ c&d </texmath>. As you can see, the element has no id attribute, and since it contains only text, there is no such attribute at all; both labels are lost. Moreover, the <texmath> has no id-text.
If you say \global\multiply\count0 by 2, the value of \count0 is globally multiplied by 2. The keyword by is optional. Instead of \count0 you can put any variable that remembers an integer, a dimension, a glue, or a muglue (in reality, the same quantity that can be put after \advance); after the optional by a number is required (and an number is an integer in this context). Multiplication may signal overflow.
If you say \dimen1=\dimen0 \dimen0=.6666\dimen1 then \dimen0 is multiplied by roughly 2/3. This method does not work for integers.
You say \put(x,y)(dx,dy){N}{object} in order to put an object
a given number of times into a picture.
See description of the
picture environment for the syntax of the
(x,y) part, and some examples.
There is one example with a ruler; it has three types of graduations: every millimeter, every 5 millimeter, every centimeter. The shortest lines were produced via: \multiput(1,0)(1,0){49}{\line(0,1){2.5}} This means: for every integer i between 0 and N-1, put a copy of the {object} at position (x+i dx, y+i dy) . In the example, the y-coordinate is always 0, the x-coordinate ranges between 1 (for i=0) to 49 (for i=48). In the same fashion, the following code \multiput(0,0)(10,0){6}{\line(0,1){5}} puts a rule a 0, 10, 20, 30, 40 and 50.
If you put a star after the command name, then Tralics translates the {object} N times. This is needed in case where the translation is not constant. For instance, the following piece of code \multiput*(10,7)(10,0){5}{ \addtocounter{cms}{1} \makebox(0,0)[b] {\arabic{cms}}} modifies the value of the counter, hence numbers 1, 2, 3, 4, and 5 are put over the rules (the object that is put in the picture is the translation of the \makebox command).
Expansion of \multispan3 is \omit\span\omit\span\omit.
This is an environment, like eqnarray, with one column instead of three, and one equation number (the equation number will be omitted by using the multline* environment of the \notag command). The content of the environment is typeset in math mode, each line being centered, the first line is flushed left, and the last line is flushed right. The commands \shoveright can be used to push a line to the left or the right. Example
\begin{multline}
\sin=\cos\\
\shoveright{\cos}\\
\shoveleft{\sin}\\
1+2
\end{multline}
<formula id-text='1' id='uid1' type='display'>
<math mode='display' xmlns='http://www.w3.org/1998/Math/MathML'>
<mtable displaystyle='true'>
<mtr><mtd columnalign='left'>
<mrow><mo form='prefix'>sin</mo>
<mo>=</mo><mo form='prefix'>cos</mo></mrow></mtd>
</mtr>
<mtr><mtd columnalign='right' columnspan='1'>
<mo form='prefix'>cos</mo></mtd></mtr>
<mtr><mtd columnalign='left' columnspan='1'>
<mo form='prefix'>sin</mo></mtd>
</mtr>
<mtr><mtd columnalign='right'>
<mrow><mn>1</mn><mo>+</mo><mn>2</mn></mrow></mtd>
</mtr>
</mtable>
</math>
</formula>
Preview: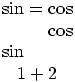 
.
(see also here).
When you say \muskip13 12mu plus 2fill, you change the value of
the muglue register number 13 to the value 12mu+2fill.
The integer must be a valid register number
(between 0 and 1023). In a construct like \mskip\muskip0,
you ask TeX for insertion of a math glue, whose value is
the content of the math glue register number zero.
See scanint for details of how
integers are read, and scanglue
for math glue.
When you say \muskipdef\foo=13, you make \foo
an alias for \muskip13.
You can put the prefix \global before \muskipdef.
See scanint for details of how
the number 13 is read; it has to be a valid register number
(between 0 and 1023).
This command reads math glue and converts it to normal glue. See \gluestretchorder for details.
back to home page
© INRIA 2003-2005, 2006, 2007
Last modified $Date: 2015/12/01 17:24:42 $