Expérimentations numériques

Le premier cas que nous allons considérer est celui pour lequel la fissure est un segment de l'axe réel. Comme nous l'avons vu, il s'agit d'un cas particulièrement favorable puisque si le saut de température change k fois de signe sur le segment, on aura tous les pôles sur la fissure à l'exception d'au plus k pôles.

**Figure:** Caractéristiques de la solution pour $\Phi(\theta)=\sin\theta$ .
[Saut de température $\sigma$ sur $\gamma$ .] $\includegraphics[width=.45\textwidth]{d1sigma.ps}$ [Rapport des valeurs singulières s_k/s_k+1.] $\includegraphics[width=.45\textwidth]{d1vs.ps}$

$\begin{displaymath} \mathcal E= \left\{ z = e_1 \cos\theta + i e_2 \sin\theta ~:~ \theta \in [0,2\pi)\right\}, \end{displaymath}$

(7.1)

La première fonction que l'on choisit comme flux $\Phi(\theta)$ sera tout d'abord un simple sinus $\Phi(\theta)=\sin\theta$ de l'argument $\theta$ . Comme on peut immédiatement le constater sur la figure 4.1 (a), le saut de température sur la fissure ne change pas de signe pour ce flux, ce qui nous donne les conditions optimales sur la convergence des pôles.

Le cas $H^\infty _N$

Les valeurs de u sont mesurées sur 1000 points du bord, et l'on estime les coefficients d'une série de Fourier tronquée entre les degrés -70 et 70.
La figure 4.1 (b) nous montre que la décroissance des dix premières valeurs singulières de l'opérateur de Hankel estimé est parfaitement géométrique. Au-delà de ce degré, les valeurs singulières semblent stagner dans un même ordre de grandeur. Un estimation de cette onzième valeur singulière nous donne environ 10^-14. Sachant que la norme $L^\infty$ de la fonction est de l'ordre de l'unité, le rapport entre ces deux valeurs correspond donc à l'ordre de précision des calculs en machine (double précision).

**Figure 4.5:** Comportement des pôles AAK pour $\Phi(\theta)=\sin\theta$ .
[Pôles de l'approximant de degré 11] $\includegraphics[width=.45\textwidth]{d1_11.ps}$ [Pôles de l'approximant de degré 12] $\includegraphics[width=.45\textwidth]{d1_12.ps}$

Observons maintenant le positionnement des pôles sur la figure 4.2. On constate que les résultats obtenus se confirment effectivement jusqu'au degré 11 puisque les pôles (représentés par des 'x') sont sans exception sur la fissure. Dès le degré suivant, en revanche, on commence à voir l'apparition de pôles hors de la fissure. Qui plus est, ce pôle ``résiduel'' semble correspondre parfaitement avec un zéro (représenté par un 'o') de l'approximant, ce qui laisse supposer que la fraction obtenue pourrait se simplifier en ce pôle.

En un sens, ceci peut apparaître comme logique en considérant une propriété des approximants AAK, selon laquelle l'erreur d'approximation f-g_N est de module constant presque partout sur $\mathbb{T}$ et égale à la valeur singulière s_N. De ce fait, ceci nous indique que lorsque s_N atteint la précision machine, l'approximant g_N coïncide avec f presque partout à la précision machine près, ce qui se traduit encore par le fait que, pour la machine, f n'est pas discernable de g_N. Il serait donc illogique d'espérer une meilleure approximation, avec les outils en présence.

Le cas H²_N

Dans un tel cas, l'approximation L² présente un intérêt moindre par rapport à l'approximation AAK. Le temps de calcul de cette dernière approche est en effet négligeable en comparaison d'un algorithme itératif comme celui que nous utilisons. Nous avons en effet pu constater que l'algorithme de Newton semble prendre ici un temps considérable dès que l'on dépasse le degré 6, principalement parce que l'approximant est déjà très proche de la fonction originale. On peut en effet voir que le critère $\left\Vert f-p/q\right\Vert _2^2/\left\Vert f\right\Vert _2^2$ vaut déjà 4,561.10^-15. Les données fournies à l'algorithme étant connues avec une précision relative de l'ordre de 10^-14, ceci explique la raison pour laquelle on pourra difficilement espérer obtenir plus de pôles.

**Figure:** Comportement des pôles H²₆ pour $\Phi(\theta)=\sin\theta$ .
[Pôles de l'approximant de degré 6] $\includegraphics[width=.45\textwidth]{droite6_l2.ps}$ [Pôles avec la fissure] $\includegraphics[width=.45\textwidth]{droite6_l2c.ps}$

Fissure sur l'axe réel avec changement de signe de la fonction saut

**Figure:** Caractéristiques de la solution pour $\Phi(\theta)=\cos\theta+2\!\cos{2\theta}+2\!\sin{2\theta}$ .
[Saut de température $\sigma$ sur $\gamma$ .] $\includegraphics[width=.45\textwidth]{d2sigma.ps}$ [Rapport des valeurs singulières s_k/s_k+1.] $\includegraphics[width=.45\textwidth]{d2vs.ps}$

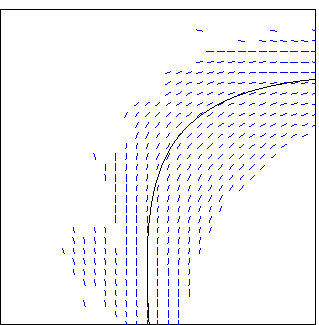
Le premier constat que l'on peut faire dans ce cas, en observant la figure 4.4 (a), est que la fonction de saut $\sigma$ change une fois de signe sur $\mathcal E$ . Selon les résultats donnés par les théorèmes 11 et 12, ceci autorise un pôle a ne pas être sur la fissure. Nous allons voir comment ce phénomène se manifeste pour notre exemple.

**Figure:** Comportement des pôles AAK pour $\Phi(\theta)=\cos\theta+2\cos{2\theta}+2\sin{2\theta}$ .
[Pôles de l'approximant de degré 9] $\includegraphics[width=.45\textwidth]{d2_9.ps}$ [Pôles de l'approximant de degré 10] $\includegraphics[width=.45\textwidth]{d2_10.ps}$

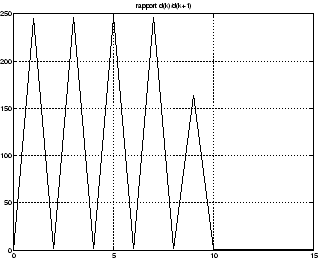
Notons sur la figure 4.4 (b) que la vitesse de décroissance des valeurs singulières est pour le moins irrégulière. En fait, il apparaît que toutes les valeurs singulières de notre fonction sont des valeurs doubles. Pour s'en convaincre, remarquons que la partie singulière de la fonction ne peut être dûe qu'au terme $2\sin 2\theta$ . En effet, puisque les autres termes, ainsi que la fissure, sont invariants en appliquant une symétrie par rapport à l'axe réel, ces termes ne pourraient de ce fait induire un saut de température sur la fissure $\gamma$ puisque les valeurs limites de u coïncident (u⁺=u^-).
De ce fait, notre problème est équivalent (à un facteur analytique près) à celui du meilleur approximant AAK de la partie singulière, à savoir l'approximant pour un flux $\Phi_s(\theta)=2\sin 2\theta$ . Or, avec un tel flux, le problème présente une symétrie centrale par rapport au centre 0 du disque $\mathbb{D}$ . Ceci induit que pour un point z sur la fissure, on a u⁺(z)=u^-(-z), ce qui entraîne en d'autres termes que le saut de température $\sigma$ est impair. Alors la partie singulière S définie en (3.54) clairement paire. Alors, si g_N(z) est le meilleur approximant AAK de S, g_N(-z) l'est aussi et par unicité g_N est pair. Il ne peut de ce fait pas avoir un nombre impair de pôles, ce qui entraîne que g_2p+1=g_2p pour tout p, ce qui implique des valeurs singulières multiples.

Toutefois, de par l'incertitude sur les évaluations numériques, elles ne le sont pas exactement (on constate une légère décroissance), ce qui donne un sens au résultat de généricité que nous évoquions en 4.2, mais il n'en reste pas moins que le pôle apparaissant lors des approximations de degré impairs ne donne aucune nouvelle information. Ce fait peut être constaté en comparant sur la figure 4.5. En fait, la figure (a) y illustre ce qui se passe pour les degrés impairs : on constate un pôle confondu avec un zéro et très nettement détaché du reste des pôles. A l'inverse, on constate que tous les pôles pour des degrés k pairs vont sur la fissure, et ce en dépit du fait que seuls k-1 soient nécessairement dessus, d'après le résultat.
Enfin, on notera dans ce cas encore que la limite numérique apparaît comme dûe à la précision machine puisque s₁₀ est là encore de l'ordre de 10^-14 alors que la norme $L^\infty$ de f estimée sur le bord vaut environ 3,36.

Cas d'une fissure non portée par un diamètre

A présent, nous allons considérer le cas plus général où la fissure est définie par un arc analytique joignant deux points non alignés avec le centre du cercle. Pour modéliser cette fissure analytique, on utilise un segment entre ces deux points, ce qui, par la combinaison avec des applications conformes, couvre finalement un nombre de cas assez conséquent. Ce segment sera défini ainsi :

$\begin{displaymath} \mathcal E= \left\{ z = 3/10 + e_1 \cos \theta + i (1/5 + e_2 \sin \theta) ~:~ \theta \in [0,2\pi)\right\}, \end{displaymath}$

(7.2)

**Figure 4.6:** Convergence des pôles AAK vers un arc géodésique, avec 70 coefficients de Fourier.
$\begin{figure} \begin{center} \subfigure[Rapport des valeurs singuli\\lq eres $s_k/... ...e $8$ .] {\epsfig{figure=geod8.ps,width=.45\textwidth}} \end{center}\end{figure}$

**Figure 4.7:** Convergence des pôles AAK vers un arc géodésique, avec 150 coefficients de Fourier.
$\begin{figure} \begin{center} \subfigure[Rapport des valeurs singuli\\lq eres $s_k/... ...12$ .] {\epsfig{figure=geodx12.ps,width=.45\textwidth}} \end{center}\end{figure}$

On constatera sur la figure 4.6 (a) que la décroissance se fait là encore de manière géométrique pour les huit premiers pôles avant de stagner sur des valeurs d'un même ordre de grandeur. En dépit de ce faible nombre de pôles, on peut constater sur la figure 4.6 (b) que les résultat est tout de même satisfaisant puisque les huit premiers pôles sont très proches de la géodésique. En revanche, il semble ici que la décroissance des pôles ne soit pas optimale par rapport à la précision du calcul puisque la huitième valeur singulière est cette fois de l'ordre de 10^-9. Cette stagnation pourrait avoir deux causes principales, à savoir d'une part la précision sur les mesures de u et d'autre part l'ordre de troncature de la série de Fourier. En augmentant ce degré de sorte d'avoir les coefficients entre -150 et 150, on peut constater ici que la deuxième hypothèse était la bonne puisque la stagnation des valeurs singulières se fait à partir de s₁₂ cette fois de l'ordre de 10^-14. Les courbes 4.7 illustrent cet état de fait.

Le cas L² présente lui aussi des résultats tout aussi satisfaisants, comme on peut le constater sur la figure 4.8 avec ceux de l'approximant L² de degré 6. Ici encore le critère décroît très vite puisque la valeur $\left\Vert f-p/q\right\Vert _2^2/\left\Vert f\right\Vert _2^2$ vaut déjà 3.51.10^-13 à l'ordre 6.

**Figure 4.8:** Convergence des pôles L² vers un arc géodésique
[Pôles de l'approximant de degré 6.] $\includegraphics[width=.45\textwidth]{geod6_l2.ps}$ [Les pôles de l'approximant et la fissure.] $\includegraphics[width=.45\textwidth]{geod6_l2c.ps}$

Bien que notre relation d'orthogonalité non-hermitienne ne nous assure qu'une convergence asymptotique des pôles de l'approximant AAK, on constate que dans des cas comme celui-ci, la convergence est en fait très satisfaisante. Cette technique est d'autant plus appréciable que le temps requis pour le calcul est très faible : effectuer une décomposition en valeurs singulières et un calcul de racines ne prend que quelques minutes pour un opérateur de Hankel tronqué à l'ordre 100. Le deuxième avantage de cette technique est que le temps de calcul ne dépend que de l'ordre de troncature. De ce fait, obtenir l'approximant d'ordre 12 ne prend pas plus de temps que celui d'ordre 2. Ceci n'est naturellement pas le cas pour l'approximation L² pour laquelle le nombre de paramètres pour la méthode de Newton croît avec le degré de l'approximant. Or dès lors que le degré dépasse un seuil (parfois de l'ordre de 7ou 8), au delà duquel la distance de la fonction échantillonée aux approximants pourraient devenir plus petite que la précision des mesures, l'algorithme peut alors rencontrer de nombreux minima locaux, ce qui entraîne une importante augmentation du temps d'itération à l'algorithme de quasi-Newton (on a pu constater jusqu'à plusieurs jours de calcul dans certains cas). Toutefois, l'absence de critère explicite ne permet pas de prévoir de tels cas.
En revanche, le calcul de l'approximant AAK, grâce à son expression explicite, s'effectue en quelques minutes. Toutefois, celui-ci souffre de certains défauts par rapport à son homologue.

Si nos expériences se montrent optimistes pour les flux et les fissures que nous étudions, il convient de garder à l'esprit que la convergence des pôles AAK n'est pas ``aussi indépendante'' de Nque celle des pôles L². Et il peut se trouver des cas où la vitesse de convergence de l'argument du facteur extérieur w_N ne sera pas assez satisfaisante. Disposer de l'approximation L² dans ce genre de cas est donc un atout indéniable.
La seconde question que l'on peut se poser est la robustesse de ces approximants face aux inévitables bruits de mesure. C'est le point que nous examinons dans ce qui suit.

Résistance des approximants au bruit de mesure

Après avoir abordé le problème de la continuité et constaté que la convergence paraît concluante pour des flux suffisamment réguliers, le problème suivant est celui de la sensibilité au bruit de nos méthodes d'approximation.

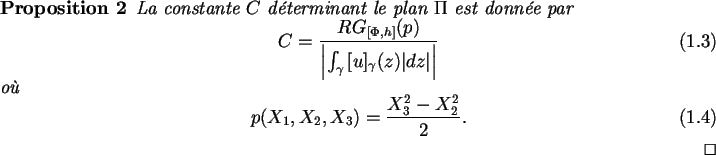A cet égard, le principe même de la méthode $H^\infty _N$ semble poser un premier problème, en ce sens que si une mesure induit une erreur $\epsilon$ , l'usage de la norme $L^\infty$ va induire pour l'approximant une obligation de ``reproduire'' l'oscillation qui en résulte, ce qui peut entrainer une perturbation importante pour un bruit ne portant que sur quelques mesures. 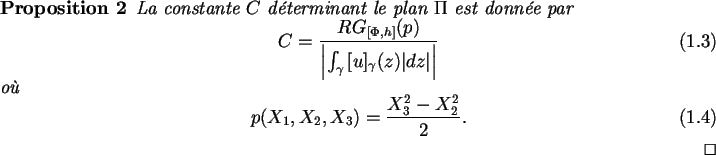En fait, on peut même facilement comprendre que dès que la valeur singulière devient plus petite que le bruit $\epsilon$ , se rapprocher des mesures reviendrait à s'éloigner de la vraie fonction f.

**Figure 4.9:** Comportement des pôles AAK avec des mesures bruitées.
$\begin{figure} \begin{center} \subfigure[Rapport des valeurs singuli\\lq eres $s_k/... ...3.] {\epsfig{figure=geodbruit3.ps,width=.45\textwidth}} \end{center}\end{figure}$

Pour vérifier ceci, reprenons l'expérimentation décrite en 4.4.3. Nous allons bruiter celles-ci en ajoutant à la valeur 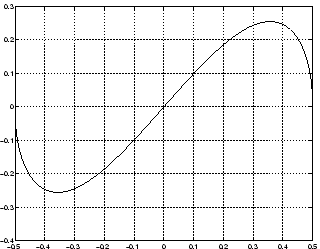$u(\theta)$ mesurée une valeur $u(\theta)\epsilon(\theta)$ ou $\epsilon$ est un bruit uniformément réparti variant entre - 10^-4 et 10^-4. Comme on le constate sur la figure 4.9, ce bruit, bien que de faible amplitude, altère assez sérieusement les résultats.
Ceci s'explique aisément en observant les valeurs singulières de l'opérateur de Hankel associé :

N	s_N
0	0,185645
1	0,0171326
2	0,00158287
3	0,000147721
4	4,81881.10^-5
5	4,42816.10^-5

Comme on le voit, les valeurs singulières atteignent l'ordre de grandeur du bruit dès l'ordre d'approximation N=4. De ce fait, il apparaît que l'on ne peut dépasser le degré 3 ou 4. La figure 4.10 illustre ce qui se passe pour le degré 4 où l'on remarque un éloignement de la géodésique, et pour les degrés supérieurs où les ``nouveaux'' pôles ne donnent manifestement plus la moindre information pertinente.

**Figure 4.10:** Comportement des pôles pour un degré élevé avec des mesures bruitées.
$\begin{figure} \begin{center} \subfigure[P\^oles de l'approximant de degr\'e 4.]... ...8.] {\epsfig{figure=geodbruit8.ps,width=.45\textwidth}} \end{center}\end{figure}$

On peut espérer un meilleur comportement de l'approximant L² dans la mesure où ce dernier cas tolère mieux les erreurs de type ``oscillatoires'' (en considérant qu'elle sont équiréparties autour de zéro, leur norme L² sera petite). Le deuxième point que nous souhaitons souligner concerne la manière dont l'approximation AAK peut permettre d'initialiser l'approximation L² afin de réduire le temps de calcul des pôles par l'algorithme itératif.

**Figure 4.11:** Comportement des pôles L² pour des mesures bruitées.
$\begin{figure} \begin{center} \subfigure[P\^oles de l'approximant de degr\'e 3.]... ... {\epsfig{figure=geodbruitl2_4.ps,width=.45\textwidth}} \end{center}\end{figure}$

Ainsi, on peut d'ores et déjà considérer un canevas d'identification où l'approximation AAK fournirait en un temps très court des points de départ pour localiser la fissure, ceux-ci initialisant un algorithme L² avant de passer à des méthodes de résoltion du problèmes direct initialisées par ces premières informations.

Vers une généralisation des résultats

Les résultats qui ont été présentés ici considèrent que la fissure est un arc de Jordan lisse entre deux points qui agissent pour f comme des points de branchement d'une fonction multivaluée. Dans ce cas, nous avons vu que le lieu d'accumulation des pôles est l'arc géodésique qui les relie l'un à l'autre (les rayons du disque en sont le cas limite).

A présent, la question qui reste à déterminer est celle de savoir ce que représente de manière générale l'arc géodésique et comment nos résultats pourraient se généraliser au cas où la fissure n'est plus un arc lisse entre deux points, mais une succession d'arcs entre p points.

En fait, on dispose déjà pour cette question d'éléments de réponse assez prometteurs. On peut en effet remarquer que l'arc géodésique $\mathcal{G}$ entre deux points $\gamma_0$ et $\gamma_1$ est aussi le contour qui minimise la capacité du condensateur formé par le couple $(\mathbb{T} ,\gamma)$ où $\gamma$ désigne une courbe continue entre $\gamma_0$ et $\gamma_1$ .
Ce lien entre la capacité d'un condensateur et l'accumulation des pôles est renforcé par un résultat que nous présentons dans le rapport [14] dans lequel nous montrons à l'aide de la relation d'orthogonalité que la répartition asymptotique des pôles converge au sens faible-* vers la distribution des charges à l'équilibre du condensateur $(\mathbb{T},\mathcal{G})$ . Ce résultat est aussi généralisé au cas des approximants L^p, pour $p \ge 2$ , dans [18].

Ainsi, on peut assez logiquement envisager que nos résultats puissent se généraliser sous la forme d'une convergence faible-* des pôles vers le contour minimisant la capacité du condensateur qui serait composé de $\mathbb{T}$ d'une part et d'un contour joignant les différents points de rupture d'analyticité.
Par ailleurs, le cas d'un contour joignant plusieurs points de branchement est le cas général d'un fissure polynômiale comme le montre la preuve du théorème 15 lorsque le relèvement de P rencontre des points critiques.
Naturellement, une telle conjecture se prête volontiers à quelques premiers tests numériques. Comme on le voit sur la figure 4.12, pour le cas de trois puis quatre points de rupture, les résultats de nos expérimentations abondent dans ce même sens, ce qui laisse présager de manière optimiste d'une généralisation prochaine de nos résultats.

**Figure 4.12:** Expérimentations pour 3 et 4 points de rupture d'analyticité
[Cas où p=3 (AAK avec 10 pôles)] $\includegraphics[width=.45\textwidth]{triangle.ps}$ [Cas où p=4 (AAK avec 14 pôles)] $\includegraphics[width=.45\textwidth]{carre.ps}$