Dans cette partie, nous allons exposer comment les équations
aux points critiques peuvent être interprétées comme une relation
dite d'orthogonalité non hermitienne, et comment par le biais de
cette dernière forme, la répartition des pôles se retrouve
étroitement liée aux propriétés géométriques du contour
d'intégration
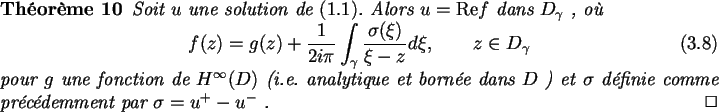 et, par voie de conséquence, à celles de
la fissure.
et, par voie de conséquence, à celles de
la fissure.
Le premier résultat que nous allons présenter ici se place sous
l'hypothèse particulière que la fissure ![]() ,
après application
conforme du domaine D sur le disque unité
,
après application
conforme du domaine D sur le disque unité
![]() ,
est un segment [b,c]porté par un diamètre du disque
,
est un segment [b,c]porté par un diamètre du disque
![]() (on effectuera au besoin une rotation
du disque pour se ramener à
(on effectuera au besoin une rotation
du disque pour se ramener à
![]() ).
).
La décomposition (3.8) devient alors
Sous les hypothèses énoncées ci-dessus, nous présentons le
résultat suivant :
![]()
![]()
Ce résultat sur le meilleur approximant
![]() est décrit
dans [15].
est décrit
dans [15].
A l'aide de notre relation d'othogonalité, nous allons montrer ici
que le résultat obtenu pour les approximants AAK reste vrai dans le
cadre L2, pourvu que l'on considère les approximants rationnels
à coefficients de Fourier réels. En effet, il n'est pas clair que
les meilleurs approximants L2 d'une fonction symterique conjuguée
de type (3.54) sur l'axe soient aussi à coefficients
réels.
Le résultat s'énonce donc ainsi :
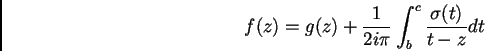

Dans ce qui suit, on adoptera une forme un peu plus générale de notre
relation d'orthogonalité (3.44) en la réécrivant comme suit :
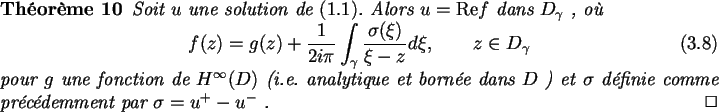 ,
cependant que
,
cependant que
 .
.
Une géodesique hyperbolique dans
![]() est un arc de cercle orthogonal
à
est un arc de cercle orthogonal
à
 .
Pour tout
.
Pour tout
 ,
on peut aisément vérifier que le lieu des
points du disque qui voient la corde
,
on peut aisément vérifier que le lieu des
points du disque qui voient la corde
![]() sous
un angle congru à
sous
un angle congru à 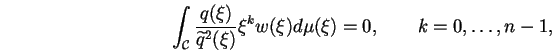 modulo
modulo ![]() ,
est une géodesique passant
par
,
est une géodesique passant
par ![]() ,
image de [-1,1] par la transformation de Möbius
,
image de [-1,1] par la transformation de Möbius
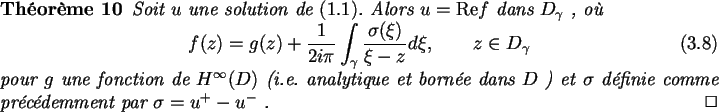 dans
dans
Nous allons montrer ici comment une relation de type (3.59) peut,
si
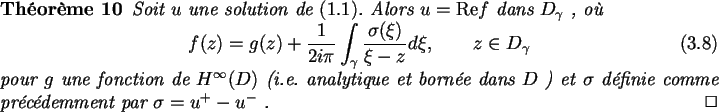 est un arc géodésique, se ramener à une relation analogue
sur l'axe réel.
est un arc géodésique, se ramener à une relation analogue
sur l'axe réel.
Supposons en effet que
![]() envoie
envoie
![]() sur
sur
![]() .
La relation (3.59) se réécrit :
.
La relation (3.59) se réécrit :
Notons hj les coefficients de qnet posons
| (6.39) |
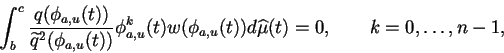 |
(6.40) |
| (6.41) |
 |
(6.42) |
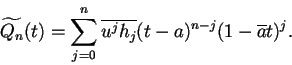 |
(6.43) |
| (6.44) |
 |
(6.45) |
 .
Ceci peut se voir en notant que les polynômes en question sont bien dans
cet espace et sont au nombre de n (ce qui est la dimension de
l'espace). Il suffit donc de montrer qu'ils sont indépendants.
.
Ceci peut se voir en notant que les polynômes en question sont bien dans
cet espace et sont au nombre de n (ce qui est la dimension de
l'espace). Il suffit donc de montrer qu'ils sont indépendants.
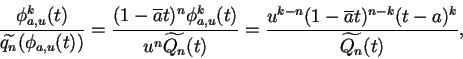 |
(6.46) |
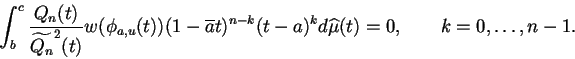 |
(6.47) |
| (6.48) |
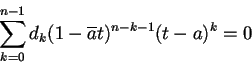 |
(6.49) |
Introduisons quelques notations qui seront souvent utilisées dans
ce qui suit.
Pour tout intervalle réel I, on notera l(I) sa longueur.
Pour toute fonction f à valeurs complexes définie sur un
intervalle I, on notera VI(f) sa variation :
 |
(6.52) |
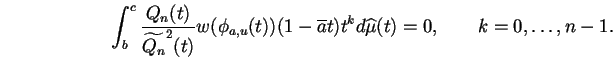 de I.
de I.
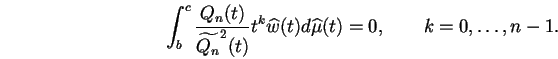 l'espace des fonctions à valeurs complexes qui sont intégrables par
rapport à
l'espace des fonctions à valeurs complexes qui sont intégrables par
rapport à
![]()
![]()
Comme nous venons de le voir dans ce qui précède, les techniques d'approximation rationnelle et méromorphe nous fournissent en principe un moyen peu coûteux de détecter la présence d'une fissure.
Si celle-ci se trouve sur un diamètre du cercle, il est aisé
d'interpréter les résultats présentés en 3.2.1
de manière physique.
On voit ainsi que, sous des conditions de régularités suffisantes,
tous les pôles de nos approximants AAK seront sur la
fissure ![]() ,
à l'exception d'un nombre au plus égal au
nombre de changements de signe sur
,
à l'exception d'un nombre au plus égal au
nombre de changements de signe sur ![]() du saut de température
du saut de température
 .
.
Notons de plus que le théorème 13 nous indique que si w est
réelle et de signe constant sur un segment réel ![]() ,
tous les
pôles d'un approximant au sens L2 sont sur
,
tous les
pôles d'un approximant au sens L2 sont sur ![]() ,
sans
nécessité de contraindre qn à avoir des coefficients réels.
Ceci entraîne en particulier que le meilleur approximant depuis H2Nd'une fonction de Markov dont la mesure satisfait les conditions du
théorème 13 (cf [14] pour une version plus générale)
a nécessairement des coefficients de Fourier réels, un fait qui n'est
pas évident a priori (mais qui découle aussi de [8])
puisque, comme nous l'avons dit, le meilleur
approximant rationnel L2 d'une fonction dont les coefficients de
Fourier sont réels ne vérifie pas automatiquement cette propriété.
,
sans
nécessité de contraindre qn à avoir des coefficients réels.
Ceci entraîne en particulier que le meilleur approximant depuis H2Nd'une fonction de Markov dont la mesure satisfait les conditions du
théorème 13 (cf [14] pour une version plus générale)
a nécessairement des coefficients de Fourier réels, un fait qui n'est
pas évident a priori (mais qui découle aussi de [8])
puisque, comme nous l'avons dit, le meilleur
approximant rationnel L2 d'une fonction dont les coefficients de
Fourier sont réels ne vérifie pas automatiquement cette propriété.
Pour le problème inverse qui nous occupe, si ![]() ne change pas
de signe et que la fissure est sur l'axe réel, on en déduit pour
l'approximation H2N, toujours si
ne change pas
de signe et que la fissure est sur l'axe réel, on en déduit pour
l'approximation H2N, toujours si
 vérifie les conditions
de régularités imposées à
vérifie les conditions
de régularités imposées à
 dans le
théorème 13, que tous les pôles sont situés sur la fissure
comme ils l'étaient pour l'approximant depuis
dans le
théorème 13, que tous les pôles sont situés sur la fissure
comme ils l'étaient pour l'approximant depuis
![]() .
.
Dans le cas plus réaliste où la fissure ![]() n'est pas portée
par un diamètre, l'interprétation est plus délicate.
Si
n'est pas portée
par un diamètre, l'interprétation est plus délicate.
Si ![]() est un arc de géodésique, les résultats énoncés
en 3.2.2 vont pouvoir être appliqués comme nous le verrons.
Toutefois, cette hypothèse est encore bien peu générale, et il
convient de nous pencher sur la question de déterminer des conditions
sous lesquelles on peut ``déformer'' le contour d'intégration
est un arc de géodésique, les résultats énoncés
en 3.2.2 vont pouvoir être appliqués comme nous le verrons.
Toutefois, cette hypothèse est encore bien peu générale, et il
convient de nous pencher sur la question de déterminer des conditions
sous lesquelles on peut ``déformer'' le contour d'intégration
 pour le ramener à l'arc géodésique sus-cité.
pour le ramener à l'arc géodésique sus-cité.
En premier lieu, considérons le cas particulier dans lequel la
fissure ![]() est un segment de droite, non porté par un diamètre.
Une fois cette droite orientée, notons
est un segment de droite, non porté par un diamètre.
Une fois cette droite orientée, notons 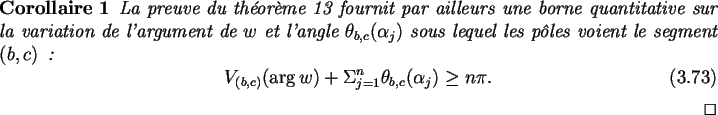 et
et ![]() respectivement
les demi-plans positifs et négatifs définis par cette orientation.
Supposons sans perte de généralité que l'arc géodésique
respectivement
les demi-plans positifs et négatifs définis par cette orientation.
Supposons sans perte de généralité que l'arc géodésique
 est situé dans
est situé dans ![]() .
En remarquant que f est analytique jusqu'à
.
En remarquant que f est analytique jusqu'à ![]() dans la région
dans la région
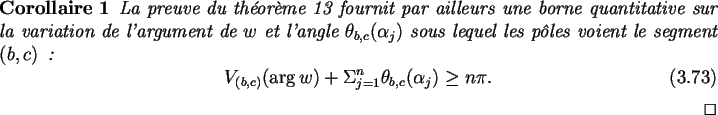 et que sa partie imaginaire est constante sur
et que sa partie imaginaire est constante sur ![]() (puisque
la dérivée de
(puisque
la dérivée de
![]() le long de
le long de ![]() n'est autre que
n'est autre que
![]() d'après la condition de Neumann),
on voit que l'on peut la prolonger analytiquement à travers
d'après la condition de Neumann),
on voit que l'on peut la prolonger analytiquement à travers ![]() en utilisant le principe de réflexion de Schwarz.
en utilisant le principe de réflexion de Schwarz.
Par conséquent,
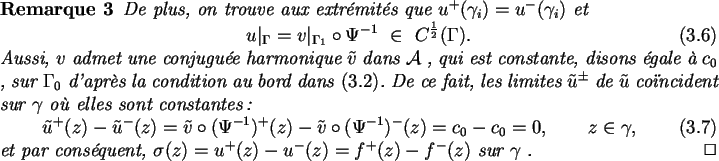 s'étend analytiquement sur un
voisinage de
s'étend analytiquement sur un
voisinage de ![]() dans
dans ![]() ,
ce qui permet de déformer
de manière correspondante le contour d'intégration de la transformée
de Cauchy (3.9) donnant la partie singulière de f.
Cependant, rien ne dit que le prolongement analytique de
,
ce qui permet de déformer
de manière correspondante le contour d'intégration de la transformée
de Cauchy (3.9) donnant la partie singulière de f.
Cependant, rien ne dit que le prolongement analytique de ![]() ainsi
obtenu s'étend jusqu'à
ainsi
obtenu s'étend jusqu'à
 .
En fait, par notre manière même de procéder, il faut et il suffit
pour qu'il en soit ainsi que le domaine d'analyticité de f+contienne le réflechi de
.
En fait, par notre manière même de procéder, il faut et il suffit
pour qu'il en soit ainsi que le domaine d'analyticité de f+contienne le réflechi de
 à travers la droite définie par
à travers la droite définie par ![]() .
Ceci n'est pas automatique car si
.
Ceci n'est pas automatique car si ![]() et
et ![]() sont proches
du cercle unité
sont proches
du cercle unité
 tout en étant très rapprochés, le
symétrique de
tout en étant très rapprochés, le
symétrique de
 par rapport à
par rapport à ![]() peut ne pas être inclus
dans le disque unité, comme on peut s'en convaincre facilement.
Ainsi, même dans le cas simple où
peut ne pas être inclus
dans le disque unité, comme on peut s'en convaincre facilement.
Ainsi, même dans le cas simple où ![]() est un segment, il
peut être nécessaire de faire des hypothèses additionnelles sur
la régularité de f, et donc de u, pour pouvoir assurer que
l'intégrale de Cauchy (3.9) peut être remplacée par une
intégrale de Cauchy du prolongement de
est un segment, il
peut être nécessaire de faire des hypothèses additionnelles sur
la régularité de f, et donc de u, pour pouvoir assurer que
l'intégrale de Cauchy (3.9) peut être remplacée par une
intégrale de Cauchy du prolongement de ![]() sur l'arc géodésique
sur l'arc géodésique
 .
Par exemple, dans la situation qui nous occupe, il est suffisant de
supposer que u est harmonique (et donc f analytique) sur un disque de
rayon
.
Par exemple, dans la situation qui nous occupe, il est suffisant de
supposer que u est harmonique (et donc f analytique) sur un disque de
rayon ![]() privé de
privé de ![]() pour que l'on puisse procéder à la
déformation désirée.
pour que l'on puisse procéder à la
déformation désirée.
En second lieu, lorsque ![]() n'est plus un segment de droite mais
l'image par une application de paramétrage d'un segment réel, qu'on
peut sans perte de généralité supposer être [0,1], le cas
le plus général que nous envisagerons est celui où l'on peut se
ramener, par changement de variable analytique, à argumenter comme
on l'a fait précédemment dans le cas d'un segment de droite.
Plus précisément, on a le théorème suivant :
n'est plus un segment de droite mais
l'image par une application de paramétrage d'un segment réel, qu'on
peut sans perte de généralité supposer être [0,1], le cas
le plus général que nous envisagerons est celui où l'on peut se
ramener, par changement de variable analytique, à argumenter comme
on l'a fait précédemment dans le cas d'un segment de droite.
Plus précisément, on a le théorème suivant :
![]()
![]()
En pratique, l'application du théorème 14 à une
fissure ![]() donnée se fait ainsi :
donnée se fait ainsi :
![]()
Dans le résultat précédent, il n'est pas important que P soit
un polynôme, hormis le fait qu'il définit un revêtement de
![]() .
Un autre résultat, plus classique, qui permet de contrôler le
domaine d'univalence d'un polynôme, cette fois en fonction du degré,
est le suivant.
.
Un autre résultat, plus classique, qui permet de contrôler le
domaine d'univalence d'un polynôme, cette fois en fonction du degré,
est le suivant.

L'usage que l'on fait de ces deux lemmes pour notre problème est le suivant :

Soulignons à nouveau que si ![]() est paramétrée par un
polynôme sur un segment autre que [0,1], il est toujours possible
de renormaliser l'intervalle de paramétrage en le segment [0,1]tout en conservant le caractère polynomial de ce paramétrage (l'effet
se répercutant alors sur P'(0)).
est paramétrée par un
polynôme sur un segment autre que [0,1], il est toujours possible
de renormaliser l'intervalle de paramétrage en le segment [0,1]tout en conservant le caractère polynomial de ce paramétrage (l'effet
se répercutant alors sur P'(0)).
La condition (3.133) ainsi que la
condition (3.134) indiquent toutes deux, en des sens
différents, que la fissure ne diffère pas trop d'une droite :
dans le cas (i), P'(z) ne doit pas trop varier dans
![]() et dans le cas (ii), n ne doit pas être trop grand par rapport
à R|P'(0)| qui renseigne sur la taille de la fissure.
et dans le cas (ii), n ne doit pas être trop grand par rapport
à R|P'(0)| qui renseigne sur la taille de la fissure.
Pour achever la présente analyse du contenu du théorème 14,
donnons à présent un résultat plus fin et entièrement géométrique
qui nécessite que l'image du paramétrage P submerge
![]() mais en
contrepartie impose uniquement des conditions sur le diamètre hyperbolique
des composantes connexes de
mais en
contrepartie impose uniquement des conditions sur le diamètre hyperbolique
des composantes connexes de
![]() .
Rappelons que la distance hyperbolique entre deux points z1 et z2de
.
Rappelons que la distance hyperbolique entre deux points z1 et z2de
![]() est donnée [43,30] par
est donnée [43,30] par
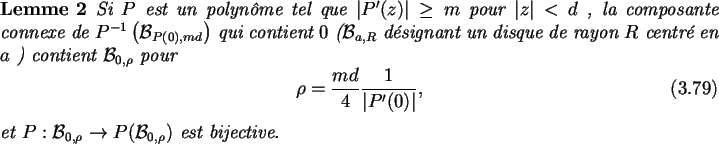 |
(6.53) |
![]()
Ayant à notre disposition, avec les théorèmes 15
et 16, quelques outils pour assurer que les conclusions
du théorème 14 sont satisfaites, nous allons, pour
le reste de ce chapitre, nous placer systématiquement dans une situation
où l'on peut appliquer ledit théorème, et en analyser les
conséquences pour ce qui est du comportement asymptotique des pôles
des approximants méromorphes et rationnels, depuis
![]() et H2Nrespectivement, au regard de l'arc géodésique
et H2Nrespectivement, au regard de l'arc géodésique
 joignant les
extrémités de la fissure
joignant les
extrémités de la fissure ![]() dans
dans
![]() .
Sous les conditions de ce théorème, le contour d'intégration
.
Sous les conditions de ce théorème, le contour d'intégration
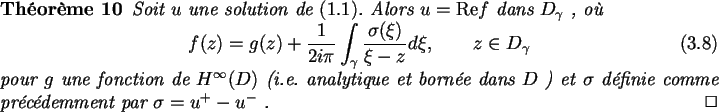 dans (3.12) peut être ramené à un arc géodésique
dans (3.12) peut être ramené à un arc géodésique
 et alors cet arc géodésique se comporte comme un lieu d'accumulation
pour les pôles de nos approximants, comme nous allons le voir maintenant.
et alors cet arc géodésique se comporte comme un lieu d'accumulation
pour les pôles de nos approximants, comme nous allons le voir maintenant.
Dans le cas des approximants L2, il apparaît en effet que la fonction
w dans l'expression (3.84) est indépendante de n.
D'après (3.44) et (3.73), celle-ci est construite
par une composition du prolongement analytique du saut de
température ![]() introduit dans le théorème 14
et d'une transformation de Möbius.
Par l'assertion (ii) dudit théorème, les hypothèses du
théorème 13 concernant w sont satifaites, et on en
déduit que le nombre de pôles hors d'un voisinage
introduit dans le théorème 14
et d'une transformation de Möbius.
Par l'assertion (ii) dudit théorème, les hypothèses du
théorème 13 concernant w sont satifaites, et on en
déduit que le nombre de pôles hors d'un voisinage
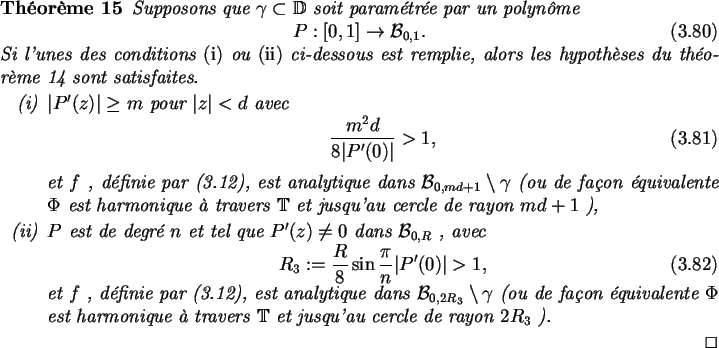 sera fini
et indépendant de n.
sera fini
et indépendant de n.
Dans le cas des approximants AAK, les choses sont un peu plus compliquées.
Comme la relation (3.52) le montre, ici, notre w fait intervenir
un facteur wN (facteur extérieur de notre vecteur singulier) qui
dépend de l'ordre N de l'approximation. Ce fait ne sera toutefois pas
trop pénalisant puisque l'on peut prouver que wN1/N converge
localement uniformément vers 1 lorsque
 et que ceci
entraîne que son argument est un
et que ceci
entraîne que son argument est un
![]() ,
ce qui combiné avec
notre résultat assure donc là encore une convergence asymptotique
des pôles dans notre voisinage
,
ce qui combiné avec
notre résultat assure donc là encore une convergence asymptotique
des pôles dans notre voisinage
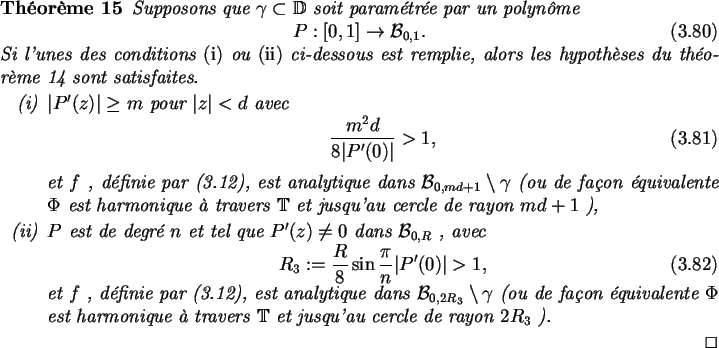 .
.
Ce dernier résultat est prouvé pour une fonction avec deux points de
branchement et dans une version plus générale qui concerne les
approximants HNp, pour ![]() ,
dans un article à paraître de
L. Baratchart et F. Seyfert [18].
Par commodité pour le lecteur, nous reproduisons ici les arguments de
cette preuve en les adaptant à notre cas, à savoir
,
dans un article à paraître de
L. Baratchart et F. Seyfert [18].
Par commodité pour le lecteur, nous reproduisons ici les arguments de
cette preuve en les adaptant à notre cas, à savoir ![]() et
une singularité en racine carrée aux extrémités.
Rappelons simplement qu'une famille normale de fonctions sur
un domaine
et
une singularité en racine carrée aux extrémités.
Rappelons simplement qu'une famille normale de fonctions sur
un domaine
 est une collection de
fonctions analytiques uniformément bornées sur tout compact.
Par un théorème classique de Montel [46], une telle famille est
relativement compacte pour la topologie de la convergence uniforme sur les
compacts de
est une collection de
fonctions analytiques uniformément bornées sur tout compact.
Par un théorème classique de Montel [46], une telle famille est
relativement compacte pour la topologie de la convergence uniforme sur les
compacts de  .
.
On peut voir de ce fait que, autant pour l'approximation H2N que pour
l'approximation
![]() ,
dès lors que le problème satisfait l'une
des hypothèses de régularité énoncées plus tôt, l'arc
géodésique se présente comme un lieu d'accumulation asymptotique pour
les approximants méromorphes.
,
dès lors que le problème satisfait l'une
des hypothèses de régularité énoncées plus tôt, l'arc
géodésique se présente comme un lieu d'accumulation asymptotique pour
les approximants méromorphes.
Les techniques employées ici sont utilisées dans [18] pour
obtenir que la répartition asymptotique des pôles converge au sens
faible-* vers la distribution des charges à l'équilibre dans un
condensateur formé par le couple
![]() .
.
Toutefois, si les techniques en questions sont analogues aux nôtres, il convient de remarquer qu'elles diffèrent de cette dernière par le choix du vecteur vN. L'article sus-mentionné considère en effet un vecteur vN dont les zéros sont exactement les pôles de l'approximant gN (l'existence d'un tel vecteur singulier découle d'un théorème de De Leuwe-Rudin [30] et est démontrée dans l'article). Les résultats étant prouvés sur les zéros de ce vecteur, ils le sont de facto sur les pôles.
Afin de simplifier la preuve, nous avons pour notre part choisi vN tel qu'il
satisfasse (3.152). Une conséquence directe de ce choix est que nous
ne pouvons plus assurer de cette manière que, si la valeur singulière sNassociée à un tel vN est multiple, tous les zéros d'un tel vecteur
sont des pôles. En fait, on peut même facilement vérifier que cette
assertion n'est jamais vraie dans ce cas. En d'autres termes, dès lors
que sN est multiple, le vecteur vN ainsi choisi possède toujours un ou
plusieurs zéros dans
![]() qui ne sont pas des pôles.
qui ne sont pas des pôles.
Si ce point n'affecte pas le résultat du théorème 13 (la borne
absolue portant sur les zéros hors d'un voisinage
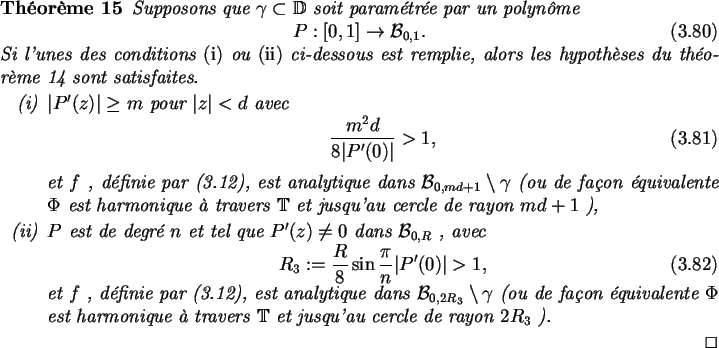 reste vraie
a fortiori pour les pôles), ceci peut sembler plus problématique dès
lors que l'on étudie la répartition asymptotique des pôles, la proportion
de zéros non-pôles pouvant altérer le résultat.
reste vraie
a fortiori pour les pôles), ceci peut sembler plus problématique dès
lors que l'on étudie la répartition asymptotique des pôles, la proportion
de zéros non-pôles pouvant altérer le résultat.
Nous allons voir ici qu'il n'en est rien, en prouvant que le nombre de ces
zéros qui ne sont pas des pôles est en réalité borné quand
 .
.
Pour voir ceci, prenons sn une valeur singulière multiple (n est choisi
tel que
sn-1>sn) et prenons à présent un vecteur singulier vnassocié à cette valeur singulière et tel que tous les zéros de vnsoient exactement les pôles de l'approximant gn.
Naturellement, vn se décompose en facteurs intérieur/extérieur sous
la forme
vn = bnwn où
![]() (avec q le polynôme
monique ayant pour racines les pôles de l'approximant AAK) mais ce vnne satisfait pas une relation du type (3.152), comme nous l'avons
mentionné précédemment. D'après [2,18], un tel vecteur
vn existe et l'on a
(avec q le polynôme
monique ayant pour racines les pôles de l'approximant AAK) mais ce vnne satisfait pas une relation du type (3.152), comme nous l'avons
mentionné précédemment. D'après [2,18], un tel vecteur
vn existe et l'on a
| (6.56) |
| (6.57) |
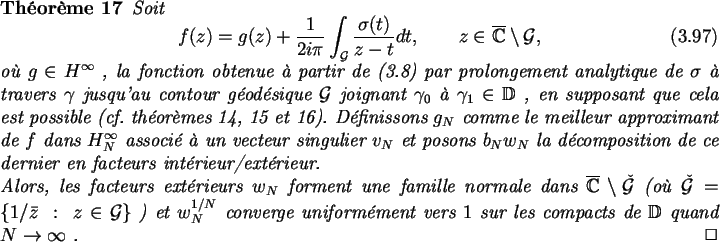 |
(6.58) |
 ,
ceci
devient
,
ceci
devient
 |
(6.59) |
 |
(6.60) |
Rappelons à présent que, même en présence de valeurs singulières
multiples, l'approximant gn ne dépend pas du choix du vecteur singulier
vn par l'unicité du meilleur approximant dans la théorie AAK.
Si donc on note ![]() l'indice par rapport à l'origine, l'indice
l'indice par rapport à l'origine, l'indice
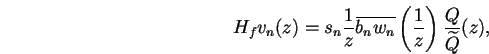 de l'erreur d'approximation s'exprime comme
de l'erreur d'approximation s'exprime comme
| (6.62) |
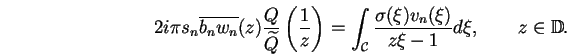 ,
et il peut se calculer comme
l'indice de son extension de Poisson sur des cercles de rayon r<1, pourvu
que r soit assez proche de 1 [42].
,
et il peut se calculer comme
l'indice de son extension de Poisson sur des cercles de rayon r<1, pourvu
que r soit assez proche de 1 [42].
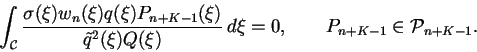 |
(6.63) |
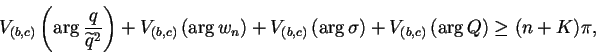 |
(6.64) |
 sont en nombre fini, et l'on peut décomposer
(3.182) et (3.183) comme le produit d'une fonction sans zéro
dans le disque et d'un nombre fini de facteurs de la forme
sont en nombre fini, et l'on peut décomposer
(3.182) et (3.183) comme le produit d'une fonction sans zéro
dans le disque et d'un nombre fini de facteurs de la forme
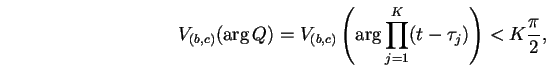 dans un voisinage du
cercle
dans un voisinage du
cercle
 privé de
privé de | (6.67) |
 ,
qui est borné de manière indépendante de n, d'après le
thèorème 17, et de même pour w.
,
qui est borné de manière indépendante de n, d'après le
thèorème 17, et de même pour w.
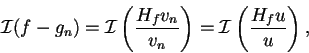 |
(6.68) |
| (6.69) |
En résumé, il est donc possible d'affirmer que
les pôles de nos deux types d'approximants de degré n s'accumulent,
lorsque
 ,
vers l'arc géodésique
,
vers l'arc géodésique
 joignant les deux
points extrémaux de la fissure
joignant les deux
points extrémaux de la fissure ![]() et même, d'après le résultat
de [14] que nous n'avons pas présenté ici, que la densité
asymptotique des pôles sur ce contour est égale à la distibution
d'équilibre du condensateur
et même, d'après le résultat
de [14] que nous n'avons pas présenté ici, que la densité
asymptotique des pôles sur ce contour est égale à la distibution
d'équilibre du condensateur
![]() .
.
Toutefois, la convergence des pôles dans le voisinage est dans les deux
cas une convergence asymptotique, et nous ne disposons pas de résultat
quantitatif général sur la vitesse de convergence des pôles en
fonction du degré n de l'approximation.
Néanmoins, les expérimentations numériques présentées dans
le chapitre suivant semblent indiquer une convergence assez rapide.
On pourra considérer un autre problème. Les résultats présentés
ici pourraient en effet apparaître comme difficilement applicables dans la
mesure où l'on suppose une connaissance des données sur tout le bord
extérieur. C'est pour cette raison qu'il nous semble important de relier
ces travaux avec un résultat présenté d'autre part par L. Baratchart,
J. Leblond et J. Partington [16]. Cet article présente une méthode
permettant d'obtenir le meilleur approximant AAK à partir du même type de
données surdéterminées u et ![]() ,
mais sur seulement une partie de
la frontière extérieure
,
mais sur seulement une partie de
la frontière extérieure ![]() .
Ces résultats nous permettent donc d'envisager une identification de
la fissure à partir de données partielles, sous une connaissance
a priori de conditions raisonnables sur la partie du bord non accessible.
.
Ces résultats nous permettent donc d'envisager une identification de
la fissure à partir de données partielles, sous une connaissance
a priori de conditions raisonnables sur la partie du bord non accessible.