


Next: Implémentation numérique de l'approximation HN
Up: Mise en pratique et
Previous: Les données
Implémentation numérique de l'approximation AAK
Nous décrivons ici comment nous mettons en 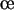 uvre le calcul du
meilleur approximant AAK. Pour cela, nous supposons une connaissance
du flux
uvre le calcul du
meilleur approximant AAK. Pour cela, nous supposons une connaissance
du flux 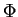 et d'un échantillonnage des valeurs correspondantes
de u sur des points du cercle unité
et d'un échantillonnage des valeurs correspondantes
de u sur des points du cercle unité
 .
Compte-tenu, d'une part des limites de la précision numérique
sur les mesures de u, et d'autre part de l'interpolation entre ses
points de mesures, plusieurs questions se posent naturellement.
La première est celle de la continuité de l'opérateur de Hankel
Hf par rapport au symbole f. La seconde, qui en découle
directement, est de savoir comment approximer la fonction
.
Compte-tenu, d'une part des limites de la précision numérique
sur les mesures de u, et d'autre part de l'interpolation entre ses
points de mesures, plusieurs questions se posent naturellement.
La première est celle de la continuité de l'opérateur de Hankel
Hf par rapport au symbole f. La seconde, qui en découle
directement, est de savoir comment approximer la fonction 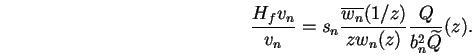 ,
et par ce biais comment approximer son opérateur de Hankel.
,
et par ce biais comment approximer son opérateur de Hankel.
Comme élément de réponse à la première question, un article de
E. Hayashi, L. N. Trefethen et M. H. Gutknecht [33] prouve que
l'opérateur de meilleure approximation de degré n qui, à
f associe gN pour la norme  ,
est continu sur l'algèbre
de Wiener
,
est continu sur l'algèbre
de Wiener
 en toute fonction f pour laquelle la (N+1)evaleur singulière l'opérateur de Hankel est simple.
en toute fonction f pour laquelle la (N+1)evaleur singulière l'opérateur de Hankel est simple.
Mentionnons aussi l'article de
V. V. Peller [41] selon lequel, toujours sous l'hypothèse que
les valeurs singulières sont simples, le meilleur approximant AAK est
continu pour les normes de Hölder et dans certains espaces de Besov.
Si cette dernière hypothèse de non-multiplicité apparaît
comme invérifiable a priori, elle reste toutefois ``génériquement''
vraie. On trouvera en effet dans [16] une preuve que l'ensemble des
fonctions f dont la (N+1)e valeur singulière est simple est un
ensemble dense dans  .
Ces résultats indiquent qu'il n'est pas suffisant en général
d'approcher f en norme uniforme pour que les approximants de Hankel
approchent ceux de f. En particulier, les techniques fondées sur
les polynômes de Jackson ou de De la Vallée-Poussin
(c.f J. R. Partington [40]) peuvent présenter des
inconvénients dûs aux oscillations qu'ils engendrent.
.
Ces résultats indiquent qu'il n'est pas suffisant en général
d'approcher f en norme uniforme pour que les approximants de Hankel
approchent ceux de f. En particulier, les techniques fondées sur
les polynômes de Jackson ou de De la Vallée-Poussin
(c.f J. R. Partington [40]) peuvent présenter des
inconvénients dûs aux oscillations qu'ils engendrent.
En ce qui concerne le mode d'approximation, il nous faut examiner
différents points. La fonction f n'étant connue que sur des
échantillons au bord, il n'est pas envisageable de connaître ses
coefficients de Fourier exactement, du moins pour sa partie réelle.
Nous avons en effet le double avantage de pouvoir contrôler le flux
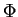 en entrée mais aussi par la même occasion, de le connaître
parfaitement, de même que sa primitive sur le bord.
en entrée mais aussi par la même occasion, de le connaître
parfaitement, de même que sa primitive sur le bord.
De fait, nos tentatives pour approcher l'opérateur de Hankel par ces
techniques n'ont pas donné de résultats probants (mauvaise
convergence).
Un deuxième inconvénient de tels modes d'approximation est qu'ils
nécessitent des points équirépartis sur le bord. Même si nous
allons souvent disposer de telles données dans nos expérimentations,
ceci peut paraître une limitation, qui nous obligerait selon les cas
à interpoler la fonction pour en calculer les coefficients ou de passer
par un changement de variable (via une application conforme du disque).
En définitive, on prendra le parti d'imposer sur le bord des flux
très lisses, sous la forme de polynômes trigonométriques de faible
degré, afin d'une part d'assurer une bonne convergence des séries
de Fourier de la partie imaginaire, et d'obtenir d'autre part une
température u assez régulière pour qu'une interpolation sur le
bord (par des techniques classiques de ``splines'' [20]) soit
raisonnablement proche de la véritable fonction.
Ainsi, l'opérateur de Hankel que l'on utilisera sera celui associé
à la troncature d'une estimation de la série de Fourier.
Selon l'ordre et le nombre de points, on calculera les coefficients
par une simple évaluation par trapèzes des intégrales
correspondantes ou, pour un nombre faible de points, en interpolant
les valeurs de u entre les points de mesures par des splines, puis
en utilisant l'expression exacte de la série de Fourier de la fonction
définie par les splines par morceaux.
Nous verrons que cette approche donne des résultats satisfaisants
dans ce cadre mais comme on peut s'y attendre, en cas de flux plus
irréguliers (discontinus, par exemple), les résultats en souffrent.
Pour évaluer jusqu'à quel degré les pôles sont significatifs,
l'approche
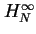 dispose dès le départ d'un critère
avantageux et peu coûteux : les valeurs singulières sN.
Pour les étudier, on pourra prendre en compte leur ordre de
grandeur et le comparer à la norme
dispose dès le départ d'un critère
avantageux et peu coûteux : les valeurs singulières sN.
Pour les étudier, on pourra prendre en compte leur ordre de
grandeur et le comparer à la norme  de f afin de
s'arréter lorsque la distance entre f et
de f afin de
s'arréter lorsque la distance entre f et
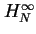 devient
inférieure à la précision machine (10-14 en double
précision). On disposera toutefois d'un outil plus ``directement''
interprétable en observant la vitesse de décroissance de ces
valeurs singulières sous la forme du rapport
sN/sN+1.
Il est en effet connu (c.f. O. G. Parfenov [38]) que la vitesse de
décroissance de ces valeurs
est au moins géométrique. De ce fait, lorsque la précision
machine est atteinte, on observera un stationnement autour de valeurs
proches de 1, ce qui donnera un degré limite au-delà duquel les
approximants ne pourront être considérés comme représentatifs.
De ce fait, comme on le voit, dés lors que la décomposition en
valeurs singulières de notre opérateur de Hankel sera effectuée,
on pourra évaluer directement les zéros portés par le vecteur
singulier vN (qui contiennent les pôles de l'approximant comme on
l'a vu) correspondant au plus haut degré accessible.
devient
inférieure à la précision machine (10-14 en double
précision). On disposera toutefois d'un outil plus ``directement''
interprétable en observant la vitesse de décroissance de ces
valeurs singulières sous la forme du rapport
sN/sN+1.
Il est en effet connu (c.f. O. G. Parfenov [38]) que la vitesse de
décroissance de ces valeurs
est au moins géométrique. De ce fait, lorsque la précision
machine est atteinte, on observera un stationnement autour de valeurs
proches de 1, ce qui donnera un degré limite au-delà duquel les
approximants ne pourront être considérés comme représentatifs.
De ce fait, comme on le voit, dés lors que la décomposition en
valeurs singulières de notre opérateur de Hankel sera effectuée,
on pourra évaluer directement les zéros portés par le vecteur
singulier vN (qui contiennent les pôles de l'approximant comme on
l'a vu) correspondant au plus haut degré accessible.
L'ensemble des calculs et opérations décrites ici seront effectuées
dans Matlab à partir des données obtenues dans notre programme
de simulation du problème direct.



Next: Implémentation numérique de l'approximation HN
Up: Mise en pratique et
Previous: Les données
Frederic Mandrea
2001-01-21
 .
Compte-tenu, d'une part des limites de la précision numérique
sur les mesures de u, et d'autre part de l'interpolation entre ses
points de mesures, plusieurs questions se posent naturellement.
La première est celle de la continuité de l'opérateur de Hankel
Hf par rapport au symbole f. La seconde, qui en découle
directement, est de savoir comment approximer la fonction
.
Compte-tenu, d'une part des limites de la précision numérique
sur les mesures de u, et d'autre part de l'interpolation entre ses
points de mesures, plusieurs questions se posent naturellement.
La première est celle de la continuité de l'opérateur de Hankel
Hf par rapport au symbole f. La seconde, qui en découle
directement, est de savoir comment approximer la fonction 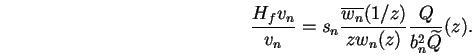 ,
et par ce biais comment approximer son opérateur de Hankel.
,
et par ce biais comment approximer son opérateur de Hankel.
 en toute fonction f pour laquelle la (N+1)evaleur singulière l'opérateur de Hankel est simple.
en toute fonction f pour laquelle la (N+1)evaleur singulière l'opérateur de Hankel est simple.