5 Analyse des robots parallèles à 3 câbles

A ce stade on a décrit le principe d'un CDPR et on a une idée des technologies qui permettent leur réalisation physique. Il faut mettre maintenant en oeuvre le système pour qu'il devienne fonctionnel c'est-à-dire répondre à des besoins comme comment le CDPR peut aller à une position, quelles sont les positions qu'il peut atteindre ...

On se focalise dans cette section sur les CDPRs à 3 câbles mais la plupart des considérations mentionnées ici s'appliquent au CDPR avec 2 câbles.

Pour cela on va supposer que l'on a construit le CDPR dont les câbles sont idéaux. Les câbles sortent du haut des mâts par des points fixes $A_i$ et sont attachés à la charge au même point $B$. Construire le CDPR revient à placer les points $A_i$ dans une position fixe dans l'espace (par exemple dans les coins d'une pièce).

5.1 Comment aller en un point ?

Évidemment un premier point d'intérêt est de pouvoir placer la charge dans un endroit donné. Il va falloir trouver un moyen de décrire cet endroit. Pour cela on va utiliser une méthode simple pour définir un endroit dans une pièce rectangulaire donnée. On choisit tout d'abord un point particulier $O$ qui sera le point au sol à l'intersection de 2 murs appelés mur 1 et 2. Pour définir un point de la pièce on va utiliser trois valeurs: la hauteur du point par rapport au sol et les distances du point au mur 1 et 2. Demander à un CDPR de mettre $B$ en un point va consister à fournir à la commande les trois valeurs du point mais il va falloir que la commande traduise cette demande en longueurs de câbles puisque c'est la seule chose qu'elle sait faire.

Nous avons déjà vu dans l'exemple des grues que la position de la charge dépendait de la longueur des câbles, c'est-à-dire de la distance entre les points $A_i$ et $B$.

Une première constatation s'impose: si vous voulez atteindre un point donné, alors les longueurs des câbles vont être fixées. Cela tient à un fait simple: les longueurs des câbles sont simplement les distances entre le point $B$ et les 3 $A_i$. Comme tous ces points sont fixés dans l'espace alors leurs distances sont elles aussi fixées. Sans entrer dans les détails on peut calculer mathématiquement qu'elle doit être la longueur des câbles pour que le CDPR aille dans une position donnée. Ce sont ces valeurs qui seront calculées par la commande qui demandera ensuite aux moteurs de tourner pour que les longueurs de câbles soient celles désirées.

Dans un monde idéal la commande va réaliser parfaitement les longueurs souhaités et le CDPR ira exactement à l'endroit désiré. Dans le monde réel les choses sont un peu plus compliqué et nous en parlerons dans la section 5.3. Mais avant d'en parler nous allons faire une première incursion dans le monde réel.

:

Le CDPR a trois câbles a été présenté vu de dessus dans la figure 5 avec les longueurs des câbles dénotés $l_1, l_2, l_3$. Comme on le voit sur la figure on a définit un repère de référence $O, {\bf x, y, z}$ et dire que l'on connaît les dimensions du robot revient à dire que les coordonnées ( $xa_i, ya_i, za_i$) des $A_i$ dans ce repère sont connues. Savoir on l'on veut aller veut dire que l'on connaît les coordonnées $(x, y, z)$ de $B$ sont connues. Si l'on écrit que la longueur $l_i$ du câble $i$ est la distance entre $A_i$ et $B$ on obtient l'équation

$$l_i^2= (x-xa_i)^2+(y-ya_i)^2+(z-za_i)^2$$ (1)

qui permet de déterminer quelle doivent être les longueurs des câbles pour atteindre une position donnée. Ce faisant nous avons établi une relation entre notre souhait (la position à atteindre) et ce que nous maîtrisons pour commander le CDPR (les longueurs des câbles). En langage robotique cette relation est appelée le modèle géométrique inverse. Pour un CDPR à deux câbles le calcul sera le même si ce n'est que nous n'aurons pas de coordonnées en $y$.

Pour illustrer numériquement certaines propriétés des CDPR à 3 câbles nous allons utiliser dans toute la suite un exemple générique en choisissant $A_1 (-2.5, 2.5, 4)$, $A_2 (-2.5, -2.5,4)$, $A_3 (2.5, -2.5,4)$. Pour le CDPR générique on suppose que la charge est telle qu'elle exerce une force purement verticale de 1 Newton.

Pour la position de $B$ (-2,-1,3.5) les $l_i$ ont comme valeurs 3.57, 1.658, 4.77.

5.2 La calibration

Le calcul de la longueur des câbles pour atteindre une position $B$ nécessite la connaissance de la position des points $A_i$ qui est donc une étape préalable à l'utilisation d'un CDPR et qu'on appelle la calibration du CDPR.

L'estimation de la géométrie d'un CDPR n'est pas forcément une tâche facile en particulier dès que l'on a à faire à un CDPR de bonne taille: les points $A_i$ ne sont peut être pas accessible facilement et/ou leurs distances à des murs de référence difficile à mesurer.

Une manière simple de réaliser cette opération est de mesurer (par exemple avec un mètre à ruban ou un télémètre laser) les distances entre les paires de point $A_i$ ainsi que les hauteurs de ces points. Une opération mathématique un peu complexe permet d'en déduire la position des points $A_i$ avec une précision qui dépendra de la qualité des mesures des distances.

: Pour un robot à 3 câbles on va supposer que les coordonnées de $A_1$ sont $(xa_1=0,ya_1=0,h_1)$, celle de $A_2$ sont $(xa_2>0,ya_2=0,h_2)$ et celle de $A_3$ $(xa_3, ya_3, h_3)$ où les $h_i$ sont les hauteurs mesurées des $A_i$. La calibration consiste donc à calculer $xa_2, xa_3, ya_3$. On mesure donc les distances entre $(A_1, A_2)$, $(A_1, A_3)$ et $(A_2, A_3)$. Pour chacune des paires $(A_i,A_j)$ on a

$$(xa_i-xa_j)^2+(ya_i -ya_j)^2+(h_i-h_j)^2 =d_{ij}^2$$

où $d_{ij}$ est la distance mesurée entre $A_i$ et $A_j$. L'équation de distance entre $A_1$ et $A_2$ a comme inconnue $xa_2^2$ seulement. Comme $xa_2>0$ on obtient

$$xa_2= \sqrt{(d_{12}^2-(h_1-h_2)^2}$$

Les deux autres équation s'écrivent:

$$\begin{eqnarray*} xa_3^2+ya_3^2+(h_1-h_3)^2-d_{13}^2 =0 \\ (xa_3-xa_2)^2+ya_3^2+(h_2-h_3)^2-d_{23}^2=0 \end{eqnarray*}$$

En soustrayant la première équation de la deuxième on obtient une équation linéaire qui n'a comme inconnue que $xa_3$: on peut donc calculer $xa_3$. La première équation va alors permettre de calculer $ya_3^2$. Il faut alors choisir une direction pour l'axe $y$ que l'on peut prendre tel que $ya_3$ soit positif. On fixe ainsi un repère de référence d'origine $A_1$ et d'axe $x$ orienté selon $A_1,A_2$.

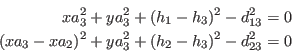
La calibration ne va pas s'arrêter là. On a vu dans la section 4.5 que l'on ne sait que mesurer la variation de longueur de câble par rapport à une valeur initiale. Lorsque l'on démarre le système il faudra donc mesurer la longueur initiale des câbles pour être capable de déterminer la longueur des câbles lors des mouvements du CDPR. A noter que l'on peut réaliser cette opération aussi après le démarrage du système: il suffit pour cela de mesurer la longueur courante, dite longueur initiale, du câble et d'obtenir la mesure du codeur, appelée mesure initiale. Par la suite la différence entre la mesure codeur et la mesure initiale permet de calculer le changement de longueur par rapport à la longueur initiale, donc la longueur courante.

Cette opération manuelle est fastidieuse et nous verrons plus loin comment procéder pour la rendre automatique.

5.3 Mais y va t'on vraiment ? La précision

Il faut être conscient des limites de la commande qui a comme objectif de mettre les câbles à une longueur donnée. Tout d'abord en raison des frottements et des jeux mécaniques il y a une limite sur le plus petit déplacement que le tambour peut effectuer. Par conséquent il y a une limite sur la variation de longueur du câble en dessous de laquelle on ne peut pas descendre: cette limite s'appelle la résolution de la commande des longueurs. A son tour cette résolution va faire qu'il sera impossible de déplacer la charge d'un point à un autre sur une distance inférieure à une limite que l'on appelle la résolution du CDPR. Sans entrer dans les détails la résolution du CDPR n'est pas constante car elle dépend de la position de la charge d'où l'on part. En pratique on l'estime expérimentalement en s'appuyant sur une analyse théorique qui en fournit une valeur approchée. La commande arrêtera le CDPR si la distance entre la position courante de la charge et celle désirée est proche de la résolution du CDPR puisque c'est le mieux qu'elle puisse faire.

La résolution n'est pas la seule chose qui empêche le CDPR d'atteindre exactement la position voulue. Nous avons déjà vu que l'on ne connaît pas exactement la position des $A_i$ et qu'il y a des erreurs sur la mesure des longueurs des câbles. En résumé pour atteindre une position de la charge donnée la commande va se tromper sur la longueur des câbles et même cette longueur ne sera pas atteinte exactement. Le CDPR n'est donc pas parfait et n'atteindra pas exactement une position désirée. On définit la précision du CDPR comme la distance entre une position de la charge désirée et celle qui est atteinte après utilisation de la commande.

Une autre conséquence est que si l'on part d'une position de la charge pour atteindre une autre position puis que l'on demande au CDPR de revenir à la position initiale il n'y reviendra pas exactement. La distance entre la position initiale et la position finale est appelée la répétabilité du CDPR.

Comme la résolution la répétabilité et la précision dépend de la position de $B$. Prenons un exemple simple en supposant en supposant que la résolution sur les longueurs des câbles soit de 2cm et que chaque câble doit être de 100cm pour atteindre la position désirée. La longueur réelle des câbles sera donc entre entre 98cm et 102cm. Supposons aussi que l'on ait mesuré la position des $A_i$ avec une précision de 1cm. Avec ces données un calcul relativement complexe permet de calculer quelle sera la distance maximum entre la position voulue et la position atteinte, ce qui donne une idée de la précision du CDPR. En pratique la précision mesurée aura une valeur qui sera en général meilleure que la précision calculée car celle-ci est la précision dans le pire des cas où toutes les erreurs s'accumulent pour éloigner la charge de la position désirée.

Toutefois les CDPR ont une propriété commune avec tous les robots parallèles qui est que toutes les erreurs mentionnées ont tendance à se moyenner en à l'inverse des structures séries où elles ont plutôt tendance à s'additionner. Ramener à une taille identique en terme de position que l'on peut atteindre les CDPR auront donc en général une précision meilleure que les robots série.

La vidéo ci-après montre comment la précision varie lorsque le CDPR monte d'une hauteur de 0.5 mètres à une hauteur de 3.8 mètres, la hauteur des mâts étant de 4 mètres et que l'on a une erreur maximale de 2cm sur la longueur des câbles. La charge est représentée par le rectangle bleu qui monte, l'échelle à gauche donne la hauteur de la charge. Les courbe à droite de la charge représentent la distance maximale en centimètre entre la position objectif et celle réellement atteinte selon chacun des axes de déplacement (en rouge selon avant/arrière, en bleu gauche/droite et en noir montée/descente). On voit par exemple que plus l'on monte plus l'erreur sur la hauteur augmente alors que les erreurs sur gauche/droite, avant/arrière diminuent graduellement.

VIDEO

: On a donné dans les équations (1) la relation entre les longueurs des câbles et la position de $B$. Si l'on dérive au premier ordre ces relations on va obtenir un système linéaire qui relie les variations de longueur des câbles $\Delta l_i$ aux variations de position $(\Delta x, \Delta y, \Delta z$) du point $B$. Cette relation peut s'écrire sous forme matricielle sous la forme

$$(\Delta l_1, \Delta l_2, \Delta l_3)^T = {\bf V} (\Delta x, \Delta y, \Delta z)^T$$

La matrice 3x3 ${\bf V}$ a comme lignes les vecteurs unitaires ${\bf n_i}={\bf A_iB}/l_i$ et donc dépend de la position de $B$. Par inversion de cette matrice on peut donc obtenir $(\Delta x, \Delta y, \Delta z$) comme fonction de $(\Delta l_1, \Delta l_2, \Delta l_3)$. Dans notre exemple chacun des $\Delta l_i$ est limité à $\pm 2$ cm. On peut donc calculer l'erreur maximale sur la position de $B$ en cm sur chacun des axes par $\Delta B_i =2\sum_{j=1}^{j=3} \vert V^{-1}(i,j)\vert$. Dans ce calcul nous n'avons pas pris en compte que la position des $A_i$ n'est pas parfaitement connue. Toutefois on peut supposer que l'erreur sur les $A_i$ est bornée. La position de $A_i$ est donc en fait $A_i+\Delta A_i$ avec $\vert\Delta A_i\vert$ inférieure ou égale à une constante. Le terme $\sum_{j=1}^{j=3}\vert V^{-1}(i,j)\vert$ a donc pas une valeur qui dépend des $\vert\Delta A_i\vert$. Dans le cas des CDPR a de deux à quatre câbles on peut calculer par une formule la valeur maximum de $\sum_{j=1}^{j=3}\vert V^{-1}(i,j)\vert$ et donc la précision du CDPR pour une position donnée. . Ce calcul n'est plus possible si le CDPR a plus de quatre câbles mais un outil mathématique appelé analyse par intervalles permet de calculer non seulement la précision pour une position donnée de la charge mais aussi l'erreur maximale lorsque la position de la charge est incluse dans un volume borné.

5.4 Peut t'on aller partout ? Un peu de mécanique

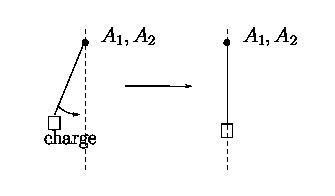
Une caractéristique des câbles est qu'ils peuvent tirer la charge mais pas la pousser. Repensons aussi à notre grue à 2 câbles: si l'on modifie la longueur des câbles la charge

aura un mouvement dans l'espace et lorsque les câbles ne changeront plus de longueur elle se stabilisera en étant dans le plan vertical qui contiendra les 2 câbles (figure 12),

Figure 12: Si la charge est tenue par 2 câbles elle va se stabiliser au bout d'un certain temps dans le plan vertical. On regarde ici les câbles de côté.

ce qui est montré dans la vidéo suivante.

VIDEO

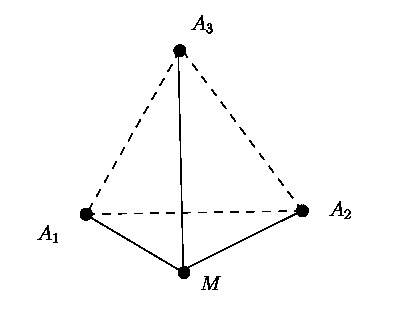
Regardons maintenant ce qui se passe vue de dessus pour un CDPR à trois câbles. La question est: peut t'on faire atteindre la position $M$ à la charge (on suppose que la longueur maximale des câbles le permet), figure 13 ?

Figure 13: Un CDPR vue de dessus. Peut t'on placer la charge dans la position $M$ qui est en dehors du triangle $A_1A_2A_3$ ?

La réponse est non: nous venons de voir que la charge tenue par les câbles 1 et 2 revient spontanément dans le plan vertical contenant $A_1, A_2$. Pour empêcher ce mouvement il faudrait donc que le câble 3 pousse la charge vers l'extérieur du triangle $A_1A_2A_3$, ce qu'un câble ne peut pas faire. La réponse serait la même si l'on plaçait $M$ au delà de l'arête $A_2A_3$ (le câble 1 devrait pousser) ou au delà de l'arête $A_1A_3$ (le câble 2 devrait pousser).

La conclusion est donc que le point représentant la charge vue de dessus ne peut être placé qu'à l'intérieur du triangle $A_1A_2A_3$.

Qu'en est t'il pour la hauteur de la charge ? il est clair que le point $B$ ne peut pas descendre plus bas que la longueur maximale que le câble peut atteindre. Pour faire simple on va supposer que points $A_i$ sont tous à la même hauteur. Il n'est pas possible de mettre le point $B$ au dessus des points $A_i$ puisque cela voudrait dire que les câbles poussent la charge vers le haut. Supposons que la charge soit maintenant sous les points $A_i$ et faites l'expérience suivante: prenez 2 poulies que vous fixez sur une table, une masse auquelle vous accrochez 2 câbles en passant l'autre extrémité du câble dans un des 2 poulies. Maintenant tirez les câbles après les poulies pour faire monter la charge. Vous allez vous rendre compte que plus la charge monte plus il va vous falloir tirer fort sur les câbles et que si vous allez jusqu'au bout de l'expérience qu'à un moment donné un câble va casser. Ce qui va donc limiter la montée de la charge est le point de rupture des câbles. Le même phénomène se produirait avec un CDPR à 3 câbles. Un CDPR ne peut donc mettre la charge que dans un volume limité de l'espace: c'est ce que l'on appelle son espace de travail.

La vidéo ci dessous montre comment évoluent les forces dans les câbles quand la charge (en bleu) monte (le haut des mâts est à une hauteur de 4 mètres)

VIDEO

Maintenant si on a des mâts suffisamment hauts et que l'on limite la hauteur du point $B$ les tensions dans les câbles vont rester limitées à une fraction de la charge: on obtiendra alors un CDPR qui pourra manipuler des charges importantes. Ainsi dans l'exemple de la vidéo, où la charge vaut 1, tant que $B$ reste à une hauteur inférieure à 2 mètres les forces dans les câbles sont toutes inférieures à 0.8. Dans notre prototype d'Ultrabot MARIONET-CRANE on pouvait monter une charge de 2.5 tonnes à une hauteur de 15 mètres. Pour MARIONET-ASSIST, destiné au transfert de personnes âgées, on peut monter 250 kg à 2 mètres.

: On va examiner l'équilibre mécanique du système au point B. La charge est soumise à la gravité, verticale, et aux 3 tensions $f_i$ des câbles qui sont dirigées selon la direction des câbles. Cette direction est définie par le vecteur ${\bf n_i}={\bf A_iB}/l_i$. L'équilibre de la charge s'écrit donc

$$(0,0,-mg)^T=\sum {\bf A_iB}/l_i f_i$$ (2)

où $mg$ est le poids, supposé connu, de la charge. Soit ${\bf U}$ la matrice de dimension 3x3 dont les colonnes sont les composantes du vecteur ${\bf A_iB}/l_i$. L'équation précédente peut s'écrire sous la forme matricielle:

$$(0,0,-mg)^T= {\bf U} (f_1, f_2, f_3)^T$$ (3)

A noter que la matrice ${\bf U}$ est la transposée de la matrice ${\bf V}$ que nous avons utilisé pour l'estimation de la précision en section 5.3.

Si l'on connaît la position de la charge on peut calculer la matrice ${\bf U}$. L'équation ci-dessus est un système linéaire dans les tensions $f_1, f_2, f_3$ que l'on peut donc calculer. Mais attention le fait que les câbles ne peut que tirer implique que les $f_i$ doivent être toutes positives ou nulles. Si la résolution du système conduit à au moins un $f_i$ négatif, alors on ne peut pas aller dans cette position. On peut alors montrer que les $f_i$ seront toutes positives uniquement si $M$ est à l'intérieur du triangle.

Pour le robot générique avec $B$ en (-2,-1,3.5) les tensions $f_i$ sont 2.14, 1.99, 0.953 pour $mg=1$. On voit que dans cette position, peu éloignée du plan des $A_i$, les tensions dans les câbles sont relativement élevées et en particulier certaines sont supérieures à la charge. Si l'on place $B$ en (-2,-1,0.5) elles deviennent 0.426, 0.658, 0.168: dans ce cas même si la tension de rupture du câble est à 1 on peut soulever la charge.

: Dans la section précédente nous avons montré la relation entre la force exercée par la charge et les tensions dans les câbles et avons montré qu'obtenir les tensions revenait à calculer l'inverse d'une matrice ${\bf U}$. Si l'on résout le système (3) chaque tension va être calculé sous la forme d'une fraction dont le dénominateur est le déterminant de la matrice ${\bf U}$. Cela implique que si ce déterminant peut tendre vers 0, alors les tensions vont tendre vers l'infini. Les endroits où le déterminant de ${\bf U}$ est nulle sont appelés les singularités du CDPR. En pratique on pourra même pas s'approcher de ces endroits puisque les câbles casseront avant. Il est donc légitime de déterminer si les singularités existent.

Prenons l'exemple du CDPR à deux câbles lorsque la charge est placée au milieu entre les deux treuils et monte verticalement. Dans ce cas l'angle entre le câble et l'horizontal est le même pour les deux câbles de valeur $w$. On peut alors montrer que le déterminant de ${\bf U}$ est proportionnel à $\sin{w}$ et s'annule donc quand $w$ est nulle, c'est-à-dire quand les câbles sont horizontaux. Plus généralement on peut montrer que le déterminant de ${\bf U}$ est nul pour toute position de $B$ sur l'horizontal entre les deux treuils: ce sont les singularités du CDPR.

On peut aussi aborder les singularités avec une autre approche. Dans la section (5.5) on va voir que la vitesse de la charge est linéairement reliée à la vitesse d'enroulement des câbles via la matrice ${\bf U^T}$ qui est la matrice transposée de ${\bf U}$. On sait que le déterminant de ${\bf U^T}$ est le même que celui de ${\bf U}$. Si on est dans une singularité et que l'on impose une vitesse nulle au câble alors on sait que la solution du système dans la vitesse de la charge peut ne pas être nulle: la charge peut bouger alors que les câbles ne changent pas de longueur !

: Pour expliquer l'augmentation des forces lorsque l'on s'approche d'une singularité on va s'intéresser à la 3ème équation du système décrit en 2, sachant que l'altitude $za_i$ a la même valeur $za$ pour tous les câbles et en supposant que le point $B$ reste en projection dans le triangle $A_1A_2A_3$. Cette équation s'écrit

$$-mg = \frac{z-za}{l_1}f_1+ \frac{z-za}{l_2}f_2+ \frac{z-za}{l_3}f_3$$

soit

$$-mg = (z-za)(\frac{f_1}{l_1}+ \frac{f_2}{l_2}+\frac{f_3}{l_3})$$

ou

$$\frac{mg}{za-z}= (\frac{f_1}{l_1}+ \frac{f_2}{l_2}+\frac{f_3}{l_3})$$

Lorsque l'on monte la charge le terme de gauche augmente très vite alors que les $l_i$ diminuent mais pas en dessous d'un seuil qui est la distance entre B et les $A_i$ quand $B$ est dans le plan horizontal. Cela implique que les $f_i$ doivent considérablement augmenter pour que l'équation soit satisfaite. Si $z=za$ les tensions $f_i$ devraient être infinies mais le câble aura cassé bien avant d'atteindre cette limite.

5.5 Et si on allait très vite ?

Maintenant intéressons nous à la vitesse de notre CDPR sachant que les treuils imposent une vitesse maximum pour l'enroulement des câbles. Intuitivement on pourrait penser que la vitesse de montée de $B$ ne peut pas être supérieure à la vitesse d'enroulement maximum des câbles mais cette intuition est fausse. Pour vérifier cela reprenons le montage à deux poulies proposé dans la section précédente. Mesurez la hauteur actuelle de votre charge puis tirez d'exactement 1cm les deux câbles: si vous mesurez alors la hauteur de votre charge vous verrez qu'elle a monté de plus d'un cm. Et plus haut vous mettez la charge au début plus la variation d'altitude de la charge va augmenter pour le même centimètre de changement de la longueur des câbles.

Mais qu'en est t'il pour les mouvements horizontaux ? le même phénomène se produit: la vitesse maximum de $B$ est un multiple de la vitesse maximum des câbles avec un facteur d'amplification qui sera toujours supérieur à 1. Ainsi pour notre prototype MARIONET-REHAB dont les câbles peuvent s'enrouler à 100 mètres par seconde la vitesse de $B$ peut atteindre plus de 400 mètres par seconde, ce qui est supérieur à la vitesse du son ! Cette propriété est commune à tous les robots parallèles. Vous en avez profité sans le savoir en mangeant votre boîte de chocolat à Pâques car très probablement les chocolats ont été empaquetés par un robot parallèle à une cadence de 40 chocolats placés dans les boîtes toutes les 8 à 16 secondes ... Un CDPR peut donc être très rapide mais il faudra trouver le bon compromis entre la vitesse et la masse de la charge déplacée. Il faut aussi voir que cette amplification de vitesse veut aussi dire que l'erreur sur la longueur des câbles va influer avec la même amplification sur la position de $B$: plus on ira vite plus il sera nécessaire d'être précis sur la mesure des longueurs des câbles pour atteindre une position de $B$ raisonnablement proche de celle désirée.

Une remarque importante pour la sécurité du CDPR: en général si la vitesse des câbles est nulle, alors la vitesse de la charge l'est aussi. Or les treuils que nous utilisons sont, en général, tels que si l'alimentation des moteurs des treuils est coupée alors le tambour ne peut plus tourner. Donc en cas de panne de courant le CDPR va rester immobile dans sa position courante, ce qui n'est pas le cas pour les robots série dont les mouvements en cas de panne de courant peuvent être dangereux. Les CDPR présentent donc un bon niveau de sécurité.

: On a vu précédemment la relation entre la force exercée en $B$ par la charge et les tensions $f_i$ dans les câbles, les deux quantités étant reliées par la matrice ${\bf U}$. Maintenant intéressons nous à la relation entre le vecteur vitesse ${\bf v}$ du point $B$ et les vitesses $\dot{l_i}$ d'enroulement/déroulement des câbles. On peut montrer que l'on a:

$$\dot{l_i}= {\bf U^T} {\bf v}$$

Par construction la matrice ${\bf U}$ est constituée de lignes qui sont les composantes d'un vecteur unitaire. Donc tous les éléments de cette matrice sont entre -1 et 1. Supposons que la vitesse désirée soit (0,0,1) et que la vitesse des câbles est contrainte à être entre -1 et 1. Le produit ${\bf U^T} {\bf v}$ conduit donc à un vecteur dont les composantes sont toutes inférieures à 1 en valeur absolu. Par exemple si $A_1 (-2.5, 2.5, 4)$, $A_2 (-2.5, -2.5,4)$, $A_3 (2.5, -2.5,4)$ et que la position de $B$ est (-2,-1,3.5) le produit ${\bf U^T} {\bf v}$ est [-0.14, -0.3,-0.1]. Ainsi en dépit que la charge se déplace à une vitesse de 1 la vitesse du câble la plus grande est juste de 0.3. SI la vitesse du câble est au maximum, donc 1, la vitesse de montée de la charge sera alors de 1/0.3=3.33. Pour la pose (-2,-1,0.5) les vitesses maximum en $x,y,z$ seraient (1.31,1.42,1.09), donc toutes supérieures à la vitesse maximale des câbles.

5.6 Où est t'on si l'on connaît les longueurs des câbles ?

Peut t'on savoir où est le point $B$ si l'on connaît la longueur des câbles ? La réponse est oui mais il va falloir faire attention à la manière dont on fera le calcul. Construisez un CDPR à 3 câbles mais en fixant les longueurs des câbles. Prenez la charge et jetez la (doucement ...). Au bout d'un certain temps le point $B$ va se stabiliser dans une position fixe. Mais pas forcément dans une position où les 3 câbles seront tendus. Par exemple si un câble a une longueur de 20cm et les autres une très grande longueur il est clair que la charge va se mettre à l'aplomb du câble le plus court, les 2 autres câbles pendant inutilement (dans le sens où il n'aide pas à porter la charge). De même si vous avez 2 câbles plutôt courts et le troisième très long le robot va se comporter comme une grue à 2 câbles et le troisième câble pendra. On peut aussi bien sûr se retrouver avec les 3 câbles tendus.

La vidéo suivante illustre ce phénomène avec un robot à 4 câbles. Ici on part d'une situation où l'on a fixé la longueur des 4 câbles et que la position initiale de $B$ est telle que les câbles sont tous détendus. On lâche alors la charge et la vidéo montre qu'elle se stabilise avec uniquement 3 câbles tendus.

VIDEO

La leçon à retenir du paragraphe précédent est que le calcul de la position de $B$ doit prendre en compte le fait que la solution peut conduire à une configuration ou un (ou plusieurs) des câbles ont une longueur qui n'est pas égale à la distance de $A_i$ à $B$ mais supérieure à celle-ci. Donc pour calculer la position de $B$ à partir des longueurs des câbles on va procéder comme James Bond sur une route enneigée, avec prudence. Pour cela on va considérer tous les cas possibles en terme de câbles tendus ou non.

On va commencer en supposant que les 3 câbles sont tendus. Une opération mathématique simple va alors permettre de trouver la position de $B$ qui conduit aux bonnes longueurs de câbles. Mais attention l'opération peut indiquer qu'il n'y a pas de solution (par exemple si un câble est très long). Supposons maintenant que cette opération a déterminé une solution: est ce la position de $B$ ?. Malheureusement non car nous n'avons considéré le problème que d'un point de vue de la géométrie alors que nous avons affaire à un système mécanique qui doit aussi satisfaire la condition d'équilibre que nous avons présenté dans la section 5.4. Par exemple si la solution géométrique est le point $M$ de la figure 13 on sait qu'elle ne satisfait pas la condition d'équilibre. Ce n'est qu'après avoir vérifié que la solution géométrique satisfait aussi la condition d'équilibre que l'on pourra dire que l'on a effectivement trouvé une position possible pour $B$.

Le processus ne s'arrête pas là et on va maintenant supposer que seulement 2 câbles sont tendus, donc examiner les où les câbles tendus sont (1,2),(1,3) et (2,3). Là aussi une opération mathématique permet de trouver une position possible de $B$ du point de vue de la géométrie. Il faudra donc là aussi vérifier si la condition d'équilibre est satisfaite. Mais ce n'est pas suffisant: il faut aussi vérifier la cohérence de notre hypothèse sur quels câbles sont tendus. Par exemple si l'on a supposé que les câble tendus étaient 1 et 2, conduisant à une solution géométrique pour la position de $B$ il va falloir vérifier que la distance entre $A_3$ et $B$ pour cette position est bien inférieure à la longueur du câble 3, supposé détendu. Si ce n'est pas le cas cette solution doit être rejetée. On examinera finalement le cas où un seul câble serait tendu, avec les même précaution de vérification concernant la longueur des câbles supposés non tendus.

Après ce processus on peut se trouver dans deux cas possibles:

1. aucune solution n'a été trouvée: cela n'interviendra que lorsque les câbles sont trop courts et que le CDPR n'est pas montable
2. dans le processus une ou des étapes ont conduit à une solution

Dans le cas particulier qui nous intéresse du CDPR à 3 câbles idéaux on peut montrer qu'en fait il n'y a qu'une solution valide et donc dès qu'une étape conduit à une solution on peut arrêter le processus puisque l'on trouvé la solution. Mais attention il ne faut pas croire que cette propriété est vraie pour tous les CDPR: par exemple un CDPR à 6 câbles dont on connaît les longueurs des câbles peut avoir jusqu'à 20 solutions pour la position de $B$ ...

Mais pour résumer dans le cas que nous traitons la mesure des longueurs des câbles nous permettra de savoir où se trouve le point $B$.

: On a vu dans une section précédente que nous avons une relation simple entre la position de $B$ et la longueur des câbles:

$$l_i^2= (x-xa_i)^2+(y-ya_i)^2+(z-za_i)^2$$

Écrivons le système complet pour chaque câble

$$(x-xa_1)^2+(y-ya_1)^2+(z-za_1)^2-l_1^2 =0$$ (4)

$$(x-xa_2)^2+(y-ya_2)^2+(z-za_2)^2-l_2^2 =0$$ (5)

$$(x-xa_3)^2+(y-ya_3)^2+(z-za_3)^2-l_3^2 =0$$ (6)

On voit que dans chacune de ces équations apparaît $x^2, y^2, z^2$. On va les éliminer simplement en construisant deux nouvelles équations en calculant (5)-(4), (6)-(4). Avec cette opération les termes $x^2, y^2, z^2$ vont disparaître et ces équations sont linéaires en $x, y$ et peuvent donc s'exprimer en fonction de $z$. Si on résout ce système et que l'on reporte le résultat dans (4) on va obtenir une équation de degré 2 en $z$ seulement. Cette équation peut avoir 2 solutions mais on peut montrer que l'une d'entre elle est supérieur à $za$ et donc n'est pas valide puisque les câbles devraient pousser $B$ vers le haut. Après avoir choisi la bonne solution en $z$ on reporte sa valeur dans les expressions de $x$ et $y$.

Par exemple pour le robot générique avec $l_1=4, l_2=3, l_3=5$ l'équation en $z$ a comme solution z=6.22, z=1.775 La première met $B$ au dessus des $A$ et peut donc être éliminée. On trouve alors x=-1.6, y=-0.7.

L'équation en $z$ peut elle ne pas avoir de solution réelle (les seules qui nous intéresse) ? Cela peut effectivement arriver et par exemple si $l_2=1$ cela sera le cas. Si l'on regarde quand s'annule le discriminant de l'équation en $z$ sans fixer de valeur pour $l_2$ on trouvera qu'il est négatif (donc l'équation n'a pas de solution réelle) si $l_2$ est inférieur à 1.006 ou est supérieur à 6.3235. La première borne dit que la longueur du câble 2 est trop courte, la 2ème que le câble 2 est trop long pour que l'équation (5) soit satisfaite. Dans ce cas on est amené à supposer que le câble 2 est détendu et l'on résout le problème en supposant que seuls les câbles 1 et 3 sont tendus. Par exemple pour $l_2$=7 on trouve y=0.45, x=-0.45 et z=1.244. La distance entre $A_2$ et $B$ est alors 4.52 et le câble 2 est effectivement détendu.

Déterminer la position de $B$ à partir des longueurs des câbles revient à établir la relation inverse de ce que nous avons appelé le modèle géométrique inverse: on appelle cette relation le modèle géométrique direct.

5.7 L'influence des poulies $\rightarrow$

Jusqu'à maintenant on a supposé que les points de sortie $A_i$ des treuils étaient fixes. Cela nous a permis de calculer facilement qu'elles étaient les longueurs des câbles pour atteindre une position donnée de $B$.

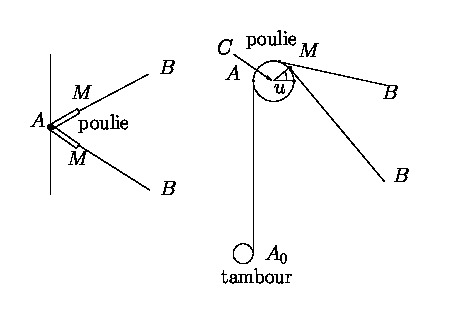
Maintenant si l'on utilise des poulies orientables comme celles montrées sur la figure 5.7 le point de sortie $M$, c'est-à-dire le point sur la poulie où le câble se dirige vers $B$, va bouger (figure 14) parce que d'une part la poulie tourne autour de son axe pour s'orienter vers $B$ (à gauche sur la figure) mais aussi car le point $M$ dépend de la proximité de $B$ avec le mât (à droite).

Figure 14: Une poulie orientable: à gauche, vue de dessus, on voit que le point de sortie $M$ de la poulie change selon la position de $B$ et à droite, vue de côté, qu'il change aussi selon la proximité de $B$ avec le mât

Jusqu'à présent on avait pu définir la longueur du câble comme la distance de $A_i$ à $B$. Maintenant comme $A_i$ est le point $M$, qui est variable, on va définir la longueur du câble comme étant celle entre le point de sortie $A_0$ du câble sur le tambour et le point $B$. Cette nouvelle définition n'a pas d'influence sur la mesure des longueurs des câbles reposant sur la mesure de la rotation du tambour, du moment que la calibration (voir section 5.2) a pu être réalisée. Cette nouvelle longueur $L$ se décompose en une partie fixe (la distance entre $A_0$ et $A$), une partie variable (la partie enroulée sur la poulie entre $A$ et $M$) et la longueur entre $M$ et $B$. Si l'on ne se soucie pas trop de précision et que le rayon de la poulie est faible par rapport à $L$ on peut négliger l'influence de la poulie et supposer que le point de sortie est en $A$. Mais si on veut améliorer la précision il faut prendre la poulie en compte. Déterminer la longueur $L$ pour atteindre une position donnée de $B$ est un peu complexe mais faisable si l'on suppose le câble tendu et la poulie parfaite. Une poulie parfaite implique qu'elle va tourner de façon à ce que les points $B$, $M$ et $A$ soit dans le même plan vertical: la position de la poulie (et donc de son centre $C$) est alors fixée. L'analyse mécanique de la poulie permet alors de montrer que le point $M$ doit être tel que la direction du câble doit être perpendiculaire à la droite passant par $C$ et $M$ et cette contrainte permet de déterminer où est $M$, donc quelle est la distance entre $M$ et $B$. Sur les 3 composantes de la longueur du câble on en connaît deux et il ne reste que la longueur entre $A$ et $M$ qui est sur la poulie, qui est facilement calculable.

La calibration (section 5.2) du codeur, qui nécessite la mesure de la longueur initiale du câble au moment du démarrage du système, est plus délicate car la mesure de la longueur est rendu difficile par la partie du câble sur la poulie. Une possibilité est de détendre tous les câbles sauf un d façon à ce que la charge soit à l'aplomb du point $M$. Si $h$ est la distance entre $A_0$ et $A$ et $d$ la différence de hauteur entre $A_0$ et $B$ alors la longueur $L$ est $2h-d+\pi r$ où $r$ est le rayon de la poulie. Une autre approche est de placer, avant montage du CDPR, une marque sur le câble à une distance connue de $B$. Pour la calibration il suffit alors de placer manuellement cette marque exactement sur le point de sortie du tambour et on a alors la longueur $L$ du câble. Ces deux approches ont l'inconvénient d'être manuelle mais nous verrons que l'on peut exploiter le principe de la marque pour le rendre automatique (voir section 8.2).

Par contre si l'on dispose de la mesure des longueurs des câbles et qu'on cherche à déterminer la position de $B$ (ce que l'on a pu faire pour un CDPR sans poulie) le calcul est très complexe: il n'y a pas de formule qui permet ce calcul et seul un algorithme sur ordinateur permet de le résoudre.

: On va voir comment calculer la longueur $L$ lorsque la position de $B$ est connue. Pour faire simple on va supposer que le repère de référence a comme origine $A_0$ et que $B$ a comme coordonnées $x_B,0,z_B$. On va alors raisonner dans le plan vertical contenant l'axe $x$ du repère. Dans ce plan $B$ a comme coordonnées $(x_B, z_B)$. Soit $C$ le centre de la poulie de coordonnées $(x_C , y_C)$, $r$ son rayon et $u$ l'angle entre l'horizontal et le vecteur ${\bf CM}$. Ce vecteur a donc comme composantes $(r\cos{u}, r\sin{u})$. Le vecteur ${\bf MB}$ a comme composantes $(x_B-x_C-r\cos{u}, z_B-z_C-r\sin{u})$. Si le câble est tendu on doit avoir

$${\bf CM}.{\bf MB}=0$$ (7)

car ${\bf CM}$ est perpendiculaire à ${\bf MB}$. Cette équation s'écrit sous la forme $v_1 \sin{u} +v_2 \cos{u}+v_3=0$, les $v_i$ étant des constantes ne dépendant pas de $u$. On peut montrer que ce type d'équation a usuellement 2 solutions en $u$. Ici l'une va être supérieure à 180 degrés et l'autre sera entre 0 et 90 degrés, solution que l'on retiendra. On peut alors calculer les coordonnées de $M$ et donc la distance entre $M$ et $B$. On a donc 2 des trois composantes de $L$. La troisième est la longueur enroulée sur la poulie entre $A$ et $M$ qui est donnée par $r(\pi-u)$: on a donc obtenu $L$ et donc résolu le modèle géométrique inverse.

Maintenant regardons le modèle géométrique direct, dans le cas simple d'un CDPR à 2 câbles. Il s'agit de déterminer $x_B, z_B$ lorsque $L_1,L_2$ sont connus. Nous avons 4 inconnues: $u_1, u_2, x_B, z_B$. La contrainte de perpendicularité (7) s'écrit pour les deux câbles:

$$(x_{C_i}-x_B)\cos{u_i}+(z_{C_i}-z_B)\sin{u_i}+r=0$$ (8)

Nous avons ensuite $L_i=L0_i+r(\pi-u_i)+\vert\vert M_iB\vert\vert$ où $L0_i$ est la distance entre $A_{0i}$ et $A_i$ et avec $\vert\vert M_iB\vert\vert^2=\vert\vert C_iB\vert\vert^2+r^2$ d'où l'on déduit

$$(x_B-x_{C_i})^2+(z_B-z_{C_i})^2+r^2=(L_i-L0_i-r(\pi-u_i))^2$$ (9)

Les 2 équations (8) sont linéaires en $x_B, z_B$ et résoudre ce système permet de se ramener à seulement 2 équations en $u_1, u_2$ en reportant la solution dans (9). Malheureusement les $u_i$ apparaissent dans ces équations sous la forme de $u_i, u_2, \cos{u_i}, \sin{u_i}$ et seule une méthode numérique peut résoudre ce genre de système. Un approche analyse par intervalles semble appropriée puisque l'on recherche des solutions entre 0 et $\pi/2$ pour $u_1, u_2$.

5.8 Les oscillations de la charge et la vibration des câbles

Dans le type de CDPR que nous étudions nous sommes partis du principe que les câbles étaient attachés tous au même point $B$. Dans la pratique il n'est pas possible de réaliser cette parfaite coïncidence. Une conséquence est que lors du mouvement du CDPR on peut avoir une rotation de la charge autour de l'axe vertical. Cette rotation sera cependant d'amplitude faible, typiquement de l'ordre de $\pm$ 10 degrés au maximum. Nous verrons plus loin qu'il est possible de mesurer cette rotation.

La conception d'un CDPR impose d'avoir un espace dégagé au dessus du point $B$, point d'attache des câbles. La charge va donc se trouver localisée en dessous de $B$. Partant d'une position arrêtée lors d'un mouvement du CDPR il est inévitable que la charge oscille. Si le mouvement est régulier cette oscillation va avoir une amplitude qui diminue progressivement. Par contre si la direction du mouvement change (typiquement quand $B$ part dans la direction opposée à sa direction précédente) les oscillations vont avoir une amplitude qui augmente avant, elle aussi, s'atténuer progressivement.

On peut éventuellement amortir ces oscillations à l'aide d'un système qui déplace des masses pour les contrecarrer. Il faut cependant pouvoir les mesurer, point que nous aborderons dans une autre section. Ces oscillations ne sont cependant pas, en général. un problème pour l'utilisation de ce type de CDPR.

La vidéo ci-dessous montre les oscillations de la charge lorsque, partant du CDPR arrêté, il se déplace tout d'abord en arrière jusqu'à atteindre une vitesse de consigne puis au bout de 30 cm prend un virage à 90 degrés pour partir à droite sur 40cm. La vidéo montre une vue en perspective, la vue de dessus puis deux vues de côte et il est préférable de la regarder en plein écran.

VIDEO

Un autre phénomène observable lorsque le CDPR déplace une charge relativement importante est que les câbles vibrent, c'est-à-dire qu'ils bougent perpendiculairement à leur axe, comme des cordes de guitare. Ces vibrations modifient très légèrement la position de la charge mais ont une influence limitée.