 |
Integer-Grid Maps for Reliable Quad Meshing
David Bommes, Marcel Campen, Hans-Christian Ebke, Pierre Alliez, Leif Kobbelt
SIGGRAPH 2013
Abstract:
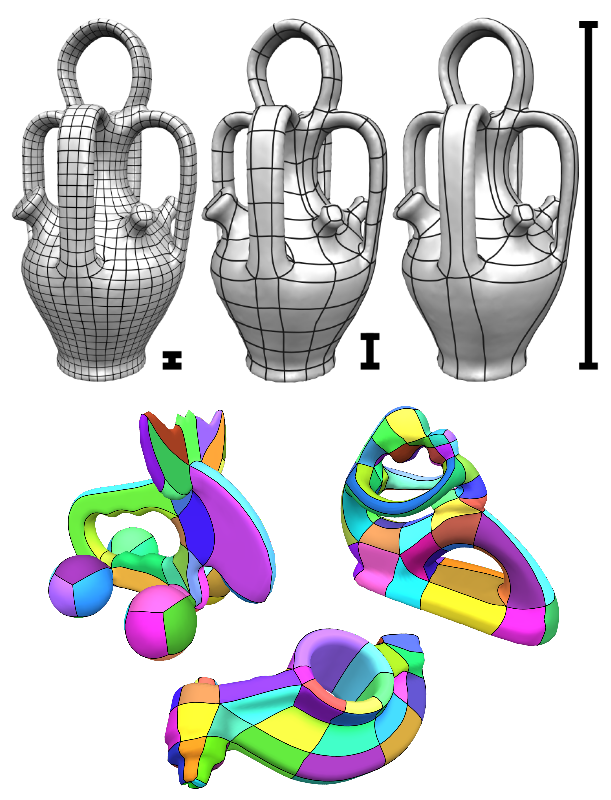
Quadrilateral remeshing approaches based on global parametrization enable many desirable mesh properties.
Two of the most important ones are (1) high regularity due to explicit control over irregular vertices and
(2) smooth distribution of distortion achieved by convex variational formulations. Apart from these strengths,
state-of-the-art techniques suffer from limited reliability on real-world input data, i.e. the determined map
might have degeneracies like (local) non-injectivities and consequently often cannot be used directly to generate
a quadrilateral mesh. In this paper we propose a novel convex Mixed-Integer Quadratic Programming (MIQP) formulation
which ensures by construction that the resulting map is within the class of so called Integer-Grid Maps that are
guaranteed to imply a quad mesh. In order to overcome the NP-hardness of MIQP and to be able to remesh typical
input geometries in acceptable time we propose two additional problem specific optimizations: a complexity reduction
algorithm and singularity separating conditions. While the former decouples the dimension of the MIQP search space
from the input complexity of the triangle mesh and thus is able to dramatically speed up the computation without inducing
inaccuracies, the latter improves the continuous relaxation, which is crucial for the success of modern MIQP optimizers.
Our experiments show that the reliability of the resulting algorithm does not only annihilate the main drawback of
parametrization based quad-remeshing but moreover enables the global search for high-quality coarse quad layouts - a
difficult task solely tackled by greedy methodologies before.
[pdf]
[bibtex]
[zip - additional material]
|
 |
QEx: Robust Quad Mesh Extraction
Hans-Christian Ebke, David Bommes, Marcel Campen, Leif Kobbelt
SIGGRAPH Asia 2013
Abstract:
The most popular and actively researched class of quad remeshing techniques is
the family of parametrization based quad meshing methods. They all strive
to generate an integer-grid map, i.e. a parametrization of the input surface
into R2 such that the canonical grid of integer iso-lines forms a
quad mesh when mapped back onto the surface in R3. An essential,
albeit broadly neglected aspect of these methods is the quad extraction
step, i.e. the materialization of an actual quad mesh from the mere “quad
texture”. Quad (mesh) extraction is often believed to be a trivial matter but
quite the opposite is true: Numerous special cases, ambiguities induced by
numerical inaccuracies and limited solver precision, as well as imperfections
in the maps produced by most methods (unless costly countermeasures are taken)
pose significant challenges to the quad extractor. We present a method to
sanitize a provided parametrization such that it becomes numerically
consistent even in a limited precision floating point representation. Based
on this we are able to provide a comprehensive and sound description of how to
perform quad extraction robustly and without the need for any complex
tolerance thresholds or disambiguation rules. On top of that we develop a
novel strategy to cope with common local fold-overs in the parametrization.
This allows our method, dubbed QEx, to generate all-quadrilateral meshes
where otherwise holes, non-quad polygons or no output at all would have been
produced. We thus enable the practical use of an entire class of maps that was
previously considered defective. Since state of the art quad meshing methods
spend a significant share of their run time solely to prevent local
fold-overs, using our method it is now possible to obtain quad meshes
significantly quicker than before. We also provide libQEx, an open source
C++ reference implementation of our method and thus significantly lower the
bar to enter the field of quad meshing.
[pdf]
[bibtex]
[zip - additional material]
[source code]
|
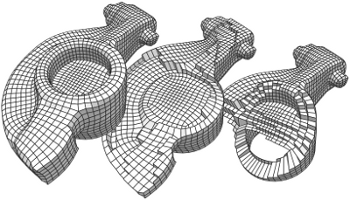 |
Advanced Automatic Hexahedral Mesh Generation from Surface Quad Meshes
Michael Kremer, David Bommes, Isaak Lim, Leif Kobbelt
22nd International Meshing Roundtable
Abstract:
A purely topological approach for the generation of hexahedral meshes from quadrilateral
surface meshes of genus zero has been proposed by M. Müller-Hannemann: in a first stage,
the input surface mesh is reduced to a single hexahedron by successively eliminating loops
from the dual graph of the quad mesh; in the second stage, the hexahedral mesh is constructed
by extruding a layer of hexahedra for each dual loop from the first stage in reverse elimination
order. In this paper, we introduce several techniques to extend the scope of target shapes of the
approach and significantly improve the quality of the generated hexahedral meshes. While the
original method can only handle "almost convex" objects and requires mesh surgery and remeshing
in case of concave geometry, we propose a method to overcome this issue by introducing the notion
of concave dual loops. Furthermore, we analyze and improve the heuristic to determine the
elimination order for the dual loops such that the inordinate introduction of interior singular
edges, i.e. edges of degree other than four in the hexahedral mesh, can be avoided in many cases.
[pdf]
[bibtex]
|
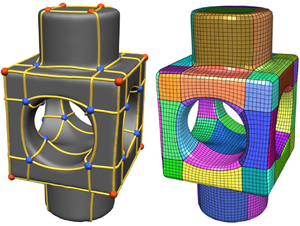 |
Dual Loops Meshing: Quality Quad Layouts on Manifolds
Marcel Campen, David Bommes, Leif Kobbelt
SIGGRAPH 2012
Abstract:
We present a theoretical framework and practical method for the automatic construction of simple,
all-quadrilateral patch layouts on manifold surfaces. The resulting layouts are coarse, surface-embedded
cell complexes well adapted to the geometric structure, hence they are ideally suited as domains
and base complexes for surface parameterization, spline fitting, or subdivision surfaces and can be
used to generate quad meshes with a high-level patch structure that are advantageous in many application
scenarios. Our approach is based on the careful construction of the layout graph's combinatorial dual.
In contrast to the primal this dual perspective provides direct control over the globally interdependent
structural constraints inherent to quad layouts. The dual layout is built from curvature-guided, crossing
loops on the surface. A novel method to construct these efficiently in a geometry- and structure-aware
manner constitutes the core of our approach.
[pdf]
[bibtex]
|
 |
Rationalization of Triangle-Based Point-Folding Structures
Henrik Zimmer, Marcel Campen, David Bommes, Leif Kobbelt
Eurographics 2012
Abstract:
In mechanical engineering and architecture, structural elements with low material consumption and
high load-bearing capabilities are essential for light-weight and even self-supporting constructions.
This paper deals with so called point-folding elements - non-planar, pyramidal panels, usually formed
from thin metal sheets, which exploit the increased structural capabilities emerging from folds or
creases. Given a triangulated free-form surface, a corresponding point-folding structure is a
collection of pyramidal elements basing on the triangles. User-specified or material-induced geometric
constraints often imply that each individual folding element has a different shape, leading to immense
fabrication costs. We present a rationalization method for such structures which respects the prescribed
aesthetic and production constraints and finds a minimal set of molds for the production process, leading
to drastically reduced costs. For each base triangle we compute and parametrize the range of feasible
folding elements that satisfy the given constraints within the allowed tolerances. Then we pose the
rationalization task as a geometric intersection problem, which we solve so as to maximize the re-use
of mold dies. Major challenges arise from the high precision requirements and the non-trivial parametrization
of the search space. We evaluate our method on a number of practical examples where we achieve rationalization
gains of more than 90%.
[pdf]
[bibtex]
|
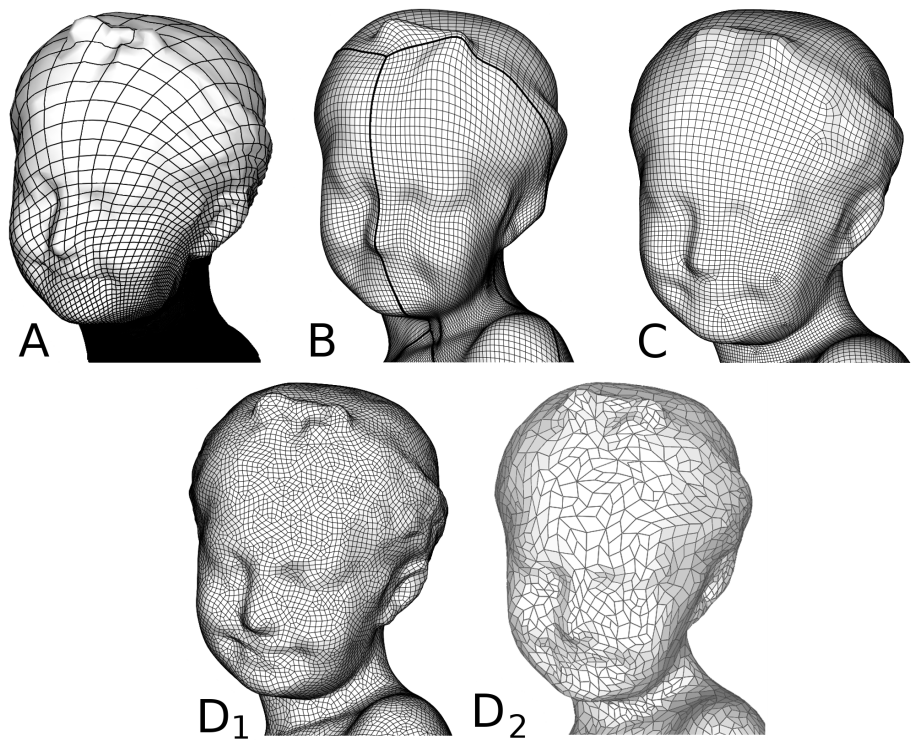 |
State of the Art in Quad Meshing
David Bommes, Bruno Lévy, Nico Pietroni, Enrico Puppo, Claudio T. Silva, Marco Tarini, Denis Zorin
Eurographics STARS 2012
Abstract:
Triangle meshes have been nearly ubiquitous in computer graphics, and a large body of data structures and
geometry processing algorithms based on them has been developed in the literature. At the same time, quadrilateral
meshes, especially semi-regular ones, have advantages for many applications, and significant progress was made in
quadrilateral mesh generation and processing during the last several years. In this State of the Art Report, we
discuss the advantages and problems of techniques operating on quadrilateral meshes, including surface analysis
and mesh quality, simplification, adaptive refinement, alignment with features, parametrization, and remeshing.
[pdf]
[bibtex]
|
 |
OpenVolumeMesh - A Versatile Index-Based Data Structure for 3D Polytopal Complexes
Michael Kremer, David Bommes, Leif Kobbelt
International Meshing Roundtable 2012, San Jose, California, USA.
Abstract:
OpenVolumeMesh is a data structure which is able to represent heterogeneous 3-dimensional polytopal
cell complexes and is general enough to also represent non- manifolds without incurring undue overhead.
Extending the idea of half-edge based data structures for two-manifold surface meshes, all faces, i.e.
the two-dimensional entities of a mesh, are represented by a pair of oriented half-faces. The concept
of using directed half-entities enables inducing an orientation to the meshes in an intuitive and
easy to use manner. We pursue the idea of encoding connectivity by storing first-order top-down
incidence relations per entity, i.e. for each entity of dimension d, a list of links to the
respective incident entities of dimension d<1 is stored. For instance, each half-face as well
as its orientation is uniquely determined by a tuple of links to its incident half-edges or
each 3D cell by the set of incident half-faces. This representation allows for handling non-manifolds
as well as mixed-dimensional mesh configurations. No entity is duplicated according to its valence, instead,
it is shared by all incident entities in order to reduce memory consumption. Furthermore, an
array-based storage layout is used in combination with direct index-based access. This guarantees
constant access time to the entities of a mesh. Although bottom-up incidence relations are implied
by the top-down incidences, our data structure provides the option to explicitly generate and cache
them in a transparent manner. This allows for accelerated navigation in the local neighbor- hood of
an entity. We provide an open-source and platform-independent implementation of the proposed data structure
written in C++ using dynamic typing paradigms. The li- brary is equipped with a set of STL compliant iterators,
a generic property system to dynamically attach properties to all entities at run-time, and a
serializer/deserializer supporting a simple file format. Due to its similarity to the OpenMesh data structure,
it is easy to use, in particular for those familiar with OpenMesh. Since the presented data structure is compact,
intuitive, and efficient, it is suitable for a variety of applications, such as meshing, visualization, and
numerical analysis. OpenVolumeMesh is open-source software licensed under the terms of the LGPL.
[pdf]
[bibtex]
[project]
|
 |
Practical Mixed-Integer Optimization for Geometry Processing
David Bommes, Henrik Zimmer, Leif Kobbelt
Special Issue of Lecture Notes in Computer Science 2012, Proceedings of Curves and Surfaces 2010
Abstract:
Solving mixed-integer problems, i.e., optimization problems where some of the unknowns are continuous while
others are discrete, is NP-hard. Unfortunately, real-world problems like e.g., quadrangular remeshing usually
have a large number of unknowns such that exact methods become unfeasible. In this article we present a greedy
strategy to rapidly approximate the solution of large quadratic mixed-integer problems within a practically
sufficient accuracy. The algorithm, which is freely available as an open source library implemented in C++,
determines the values of the discrete variables by successively solving relaxed problems. Additionally the
specification of arbitrary linear equality constraints which typically arise as side conditions of the optimization
problem is possible. The performance of the base algorithm is strongly improved by two novel extensions which are (1)
simultaneously estimating sets of discrete variables which do not interfere and (2) a fill-in reducing reordering of
the constraints. Exemplarily the solver is applied to the problem of quadrilateral surface remeshing, enabling a great
flexibility by supporting different types of user guidance within a real-time modeling framework for input surfaces
of moderate complexity.
[pdf]
[bibtex]
[project]
|
 |
Global Structure Optimization of Quadrilateral Meshes
David Bommes, Timm Lempfer, Leif Kobbelt
Eurographics 2011 (best paper award)
Abstract:
We introduce a fully automatic algorithm which optimizes the high-level structure of a given quadrilateral
mesh to achieve a coarser quadrangular base complex. Such a topological optimization is highly desirable,
since state-of-the-art quadrangulation techniques lead to meshes which have an appropriate singularity
distribution and an anisotropic element alignment, but usually they are still far away from the high-level
structure which is typical for carefully designed meshes manually created by specialists and used e.g. in
animation or simulation. In this paper we show that the quality of the high-level structure is negatively
affected by helical configurations within the quadrilateral mesh. Consequently we present an algorithm which
detects helices and is able to remove most of them by applying a novel grid preserving simplification operator
(GP-operator) which is guaranteed to maintain an all-quadrilateral mesh. Additionally it preserves the given
singularity distribution and in particular does not introduce new singularities. For each helix we construct
a directed graph in which cycles through the start vertex encode operations to remove the corresponding helix.
Therefore a simple graph search algorithm can be performed iteratively to remove as many helices as possible
and thus improve the high-level structure in a greedy fashion. We demonstrate the usefulness of our automatic
structure optimization technique by showing several examples with varying complexity.
[pdf]
[bibtex]
[zip - additional material]
|
 |
Mixed-Integer Quadrangulation
David Bommes, Henrik Zimmer, Leif Kobbelt
SIGGRAPH 2009
Abstract:
We present a novel method for quadrangulating a given triangle mesh. After constructing an as smooth as
possible symmetric cross field satisfying a sparse set of directional constraints (to capture the geometric
structure of the surface), the mesh is cut open in order to enable a low distortion unfolding. Then a seamless
globally smooth parametrization is computed whose iso-parameter lines follow the cross field directions.
In contrast to previous methods, sparsely distributed directional constraints are sufficient to automatically
determine the appropriate number, type and position of singularities in the quadrangulation. Both steps of
the algorithm (cross field and parametrization) can be formulated as a mixed-integer problem which we solve
very efficiently by an adaptive greedy solver. We show several complex examples where high quality quad meshes
are generated in a fully automatic manner.
The Constrained Mixed-Integer Solver used in this project has been released under GPL and can be found on its
projects page.
[pdf]
[bibtex]
[zip - additional material]
|
 |
Quadrangular Parameterization for Reverse Engineering
David Bommes, Tobias Vossemer, Leif Kobbelt
Special Issue of Lecture Notes in Computer Science 2009 Proceedings of Curves and Surfaces 2008
Abstract:
The aim of Reverse Engineering is to convert an unstructured representation of a geometric object, emerging e.g.
from laser scanners, into a natural, structured representation in the spirit of CAD models, which is suitable
for numerical computations. Therefore we present a user-controlled, as isometric as possible parameterization
technique which is able to prescribe geometric features of the input and produces high-quality quadmeshes with
low distortion. Starting with a coarse, user-prescribed layout this is achieved by using affine functions for
the transition between non-orthogonal quadrangular charts of a global parameterization. The shape of each chart
is optimized non-linearly for isometry of the underlying parameterization to produce meshes with low edge-length
distortion. To provide full control over the meshing alignment the user can additionally tag an arbitrary subset
of the layout edges which are guaranteed to be represented by enforcing them to lie on iso-lines of the
parameterization but still allowing the global parameterization to relax in the direction of the iso-lines.
[pdf]
[bibtex]
|
 |
Accurate Computation of Geodesic Distance Fields for Polygonal Curves on Triangle Meshes
David Bommes, Leif Kobbelt
VMV 2007
Abstract:
We present an algorithm for the efficient and accurate computation of geodesic distance fields on triangle meshes.
We generalize the algorithm originally proposed by Surazhsky et al. . While the original algorithm is able to compute
geodesic distances to isolated points on the mesh only, our generalization can handle arbitrary, possibly open,
polygons on the mesh to define the zero set of the distance field. Our extensions integrate naturally into the
base algorithm and consequently maintain all its nice properties. For most geometry processing algorithms, the
exact geodesic distance information is sampled at the mesh vertices and the resulting piecewise linear interpolant
is used as an approximation to the true distance field. The quality of this approximation strongly depends on the
structure of the mesh and the location of the medial axis of the distance fild. Hence our second contribution is
a simple adaptive refinement scheme, which inserts new vertices at critical locations on the mesh such that the
final piecewise linear interpolant is guaranteed to be a faithful approximation to the true geodesic distance field.
[pdf]
[bibtex]
|
 |
Efficient Linear System Solvers for Mesh Processing
Mario Botsch, David Bommes, Leif Kobbelt
Invited paper at XIth IMA Conference on the Mathematics of Surfaces
Abstract:
The use of polygonal mesh representations for freeform geometry enables the formulation of many important
geometry processing tasks as the solution of one or several linear systems. As a consequence, the key
ingredient for efficient algorithms is a fast procedure to solve linear systems. A large class of
standard problems can further be shown to lead more specifically to sparse, symmetric, and positive
definite systems, that allow for a numerically robust and efficient solution. In this paper we discuss
and evaluate the use of \emph{sparse direct solvers} for such kind of systems in geometry processing
applications, since in our experiments they turned out to be superior even to highly optimized multigrid
methods, but at the same time were considerably easier to use and implement. Although the methods we
present are well known in the field of high performance computing, we observed that they are in practice
surprisingly rarely applied to geometry processing problems.
[pdf]
[bibtex]
|
 |
GPU-based Tolerance Volumes for Mesh Processing
Mario Botsch, David Bommes, Christoph Vogel, Leif Kobbelt
Proc. Pacific Graphics, 237-243, 2004
Abstract:
In an increasing number of applications triangle meshes represent a flexible and efficient alternative to
traditional NURBS-based surface representations. Especially in engineering applications it is crucial to
guarantee that a prescribed approximation tolerance to a given reference geometry is respected for any
combination of geometric algorithms that are applied when processing a triangle mesh. We propose a simple
and generic method for computing the distance of a given polygonal mesh to the reference surface, based
on a linear approximation of its signed distance field. Exploiting the hardware acceleration of modern
GPUs allows us to perform up to 3M triangle checks per second, enabling real-time distance evaluations
even for complex geometries. An additional feature of our approach is the accurate high-quality distance
visualization of dynamically changing meshes at a rate of 15M triangles per second. Due to its generality,
the presented approach can be used to enhance any mesh processing method by global error control,
guaranteeing the resulting mesh to stay within a prescribed error tolerance. The application examples
that we present include mesh decimation, mesh smoothing and freeform mesh deformation.
[pdf]
[bibtex]
[slides]
|

