Considérons, sur la frontière extérieure ![]() d'un domaine
d'un domaine
![]() fissuré en
fissuré en ![]() ,
une fonction F construite à partir
de données
,
une fonction F construite à partir
de données ![]() par la formule (2.16).
F est alors la trace d'une
fonction analytique f de type (2.14). Nous allons présenter ici
une représentation de cette fonction f, et plus particulièrement
de sa partie singulière, par les résultats suivants.
par la formule (2.16).
F est alors la trace d'une
fonction analytique f de type (2.14). Nous allons présenter ici
une représentation de cette fonction f, et plus particulièrement
de sa partie singulière, par les résultats suivants.
Pour nous ramener à une interprétation physique, on voit que dans le cadre
d'une équation de la chaleur, ![]() s'interprête comme un saut de
température au travers de la fissure
s'interprête comme un saut de
température au travers de la fissure ![]() qui agit comme un isolant
parfait.
qui agit comme un isolant
parfait.
Enfin, on remarquera que comme ![]() peut être prolongée analytiquement
au travers de
peut être prolongée analytiquement
au travers de ![]() ,
on peut prolonger
,
on peut prolonger ![]() (parce que
(parce que
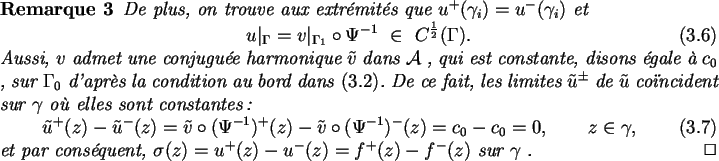 ,
comme l'indique la remarque 3) en déformant
,
comme l'indique la remarque 3) en déformant ![]() analytiquement
vers un arc voisin
analytiquement
vers un arc voisin
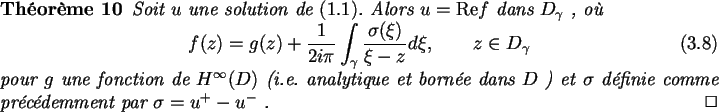 joignant
joignant ![]() à
à ![]() ,
de sorte à
obtenir
,
de sorte à
obtenir
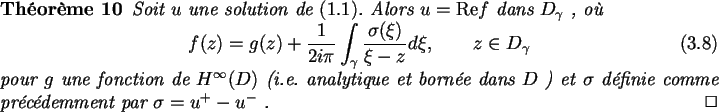 tout en conservant notre
décomposition.
tout en conservant notre
décomposition.
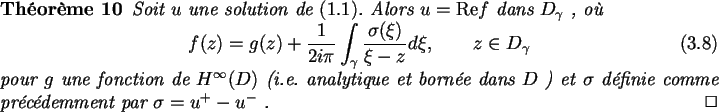 pourra être ramené à un contour bien particulier pour le problème
qui nous intéresse : un arc de géodésique hyperbolique, c'est
à dire, dans le cas du disque
pourra être ramené à un contour bien particulier pour le problème
qui nous intéresse : un arc de géodésique hyperbolique, c'est
à dire, dans le cas du disque
 joignant
joignant
Pour l'heure, forts de cette décomposition, nous allons voir dans ce qui
suit qu'elle entraîne une relation dite ``d'orthogonalité (non
hermitienne)'' sur notre contour
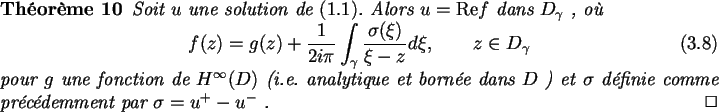 ,
valable pour les deux types
d'approximants HpN de F, pour p=2 ou
,
valable pour les deux types
d'approximants HpN de F, pour p=2 ou ![]() .
.
Soit f comme définie en (2.14).
Comme nous l'avons souligné en 2.3, le meilleur approximant
![]() de f est
gN = PH2(f)+rN où
de f est
gN = PH2(f)+rN où
![]() est le
meilleur approximant de
est le
meilleur approximant de
![]() .
.
De ce fait, en observant la décomposition (3.12), et puisque
![]() ,
il apparaît que trouver le meilleur
approximant dans H2N de f revient à trouver le meilleur approximant
dans RN de sa partie singulière
,
il apparaît que trouver le meilleur
approximant dans H2N de f revient à trouver le meilleur approximant
dans RN de sa partie singulière
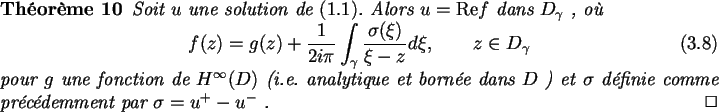 est un arc de Jordan inclus dans
est un arc de Jordan inclus dans
Dans la mesure où l'on ne cherche à étudier que les pôles de notre
approximant, nous pouvons donc nous ramener dans ce qui suit au cas pour
lequel g=0, et chercher directement le meilleur approximant rationnel
de
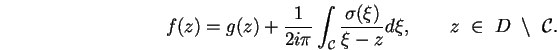 .
.
On désignera par
![]() l'espace des polynômes de degré au
plus n à coefficients complexes.
l'espace des polynômes de degré au
plus n à coefficients complexes.
Notons p et q deux polynômes de degrés respectifs au plus n-1et n tels que p/q réalise le meilleur approximant rationnel de fau sens de la norme L2, c'est-à-dire :
 et de
la relation de Parseval que p/q doit également être analytique pour
et de
la relation de Parseval que p/q doit également être analytique pour
 et que, de plus,
et que, de plus,
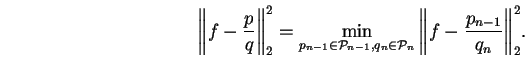 .
.
![]()
![]()
Comme on vient de le voir, si
![]() alors
alors
![]() ,
on peut
alors toujours supposer par normalisation que q est monique et écrire
,
on peut
alors toujours supposer par normalisation que q est monique et écrire
| (6.4) |
Nous allons à présent démontrer que pour tout polynôme A2n-1 de
![]() ,
il existe Bn-1 et Cn-1, tous deux de degré au plus
n-1, tels que
,
il existe Bn-1 et Cn-1, tous deux de degré au plus
n-1, tels que
| A2n-1 = p Bn-1 + q Cn-1. | (6.7) |
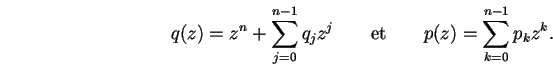 )
constituent
une base de cet espace. Etant donné qu'il y a 2n termes, il suffit de
vérifier que ceux-ci sont indépendants.
)
constituent
une base de cet espace. Etant donné qu'il y a 2n termes, il suffit de
vérifier que ceux-ci sont indépendants.
Supposons donc qu'il existe une combinaison linéaire non nulle les annulant.
Ceci s'exprime aussi en écrivant qu'il existe deux polynômes Q et R(dont au moins l'un n'est pas nul) de degré au plus n-1 tels que
Les zkp et zjq, pour
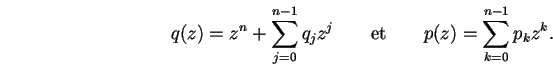 ,
forment donc une base de
,
forment donc une base de
![]() ,
ce qui nous permet de réécrire la relation (3.24)
sous la forme suivante :
,
ce qui nous permet de réécrire la relation (3.24)
sous la forme suivante :
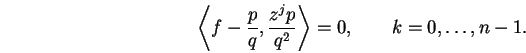 .
Montrons que l'on
peut découper cet espace en une somme orthogonale :
.
Montrons que l'on
peut découper cet espace en une somme orthogonale :
| (6.10) |
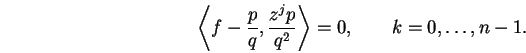 de
dimension n, il reste à prouver leur orthogonalité, à savoir que
de
dimension n, il reste à prouver leur orthogonalité, à savoir que
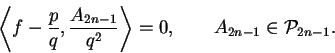 |
(6.12) |
 ,
ce qui simplifie l'intégrale pour donner à (3.30) la forme équivalente :
,
ce qui simplifie l'intégrale pour donner à (3.30) la forme équivalente :
 |
(6.13) |
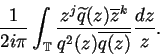 |
(6.14) |
| (6.15) |
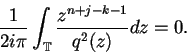 |
(6.17) |
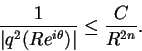 |
(6.18) |
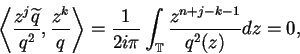 |
(6.19) |
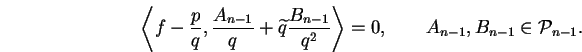 sur
sur
 ,
on a
,
on a
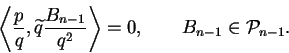 |
(6.20) |
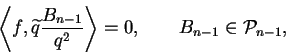 |
(6.21) |
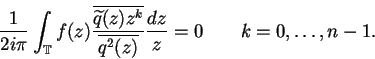 |
(6.22) |
| (6.23) |
| (6.24) |
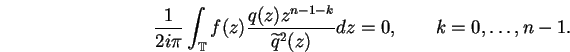 est donc analytique dans le disque, et l'on peut alors appliquer la formule
de Cauchy pour obtenir finalement l'équation :
est donc analytique dans le disque, et l'on peut alors appliquer la formule
de Cauchy pour obtenir finalement l'équation :
Cette équation, dite équation aux points critiques, traduit qu'un
polynôme q de degré n est le dénominateur d'un fraction
irréductible p/q qui est elle-même un point critique (i.e. un
point où la dérivée s'annule) de (3.14), l'erreur en
approximation rationnelle L2.
Nous détaillerons dans les sections suivantes de quelle manière nous
pouvons exploiter une telle relation afin d'obtenir des renseignements sur
la position des pôles de notre approximant par rapport au contour
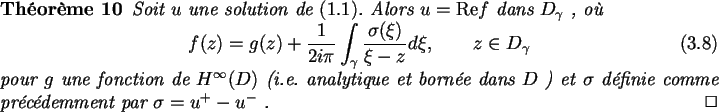 .
.
Nous allons considérer ici gN l'approximant AAK de degré N,
toujours pour une fonction f telle que nous l'avons définie
en (3.9).
Puisque g est dans ![]() ,
on peut constater que l'opérateur
de Hankel Hf associé à notre fonction est l'opérateur de
Hankel HS associé à S définie en (3.13).
De ce fait, les pôles de l'approximant gN dépendent uniquement de
la partie singulière S. Nous pourrons donc supposer, comme dans le cas
précédent, que g=0 sans altérer notre résultat.
Nous rappelons que l'approximant AAK est donné par la formule explicite
,
on peut constater que l'opérateur
de Hankel Hf associé à notre fonction est l'opérateur de
Hankel HS associé à S définie en (3.13).
De ce fait, les pôles de l'approximant gN dépendent uniquement de
la partie singulière S. Nous pourrons donc supposer, comme dans le cas
précédent, que g=0 sans altérer notre résultat.
Nous rappelons que l'approximant AAK est donné par la formule explicite
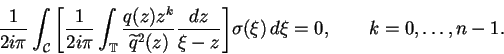 |
(6.26) |
 |
(6.28) |
| (6.29) |
| (6.30) |
Notons n le plus petit entier que sn=sN.
De par la théorie AAK, on sait que vN a au moins n zéros dans
![]() .
Par ailleurs, il résulte de (3.50) que vN est analytique
à travers
.
Par ailleurs, il résulte de (3.50) que vN est analytique
à travers
 de sorte que ce nombre de zéros, que nous noterons N0,
est fini.
Désignons par
de sorte que ce nombre de zéros, que nous noterons N0,
est fini.
Désignons par
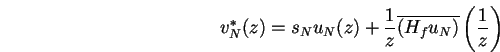 cette suite de zéros qui
contient nécessairement les pôles (Il est possible que certains
des zéros en question se simplifient avec le numérateur ;
ceci ne pourra toutefois pas arriver dès lors que la valeur singulière
sN est simple) de notre approximant gN d'après la
relation (2.28).
En notant q le polynôme unitaire
cette suite de zéros qui
contient nécessairement les pôles (Il est possible que certains
des zéros en question se simplifient avec le numérateur ;
ceci ne pourra toutefois pas arriver dès lors que la valeur singulière
sN est simple) de notre approximant gN d'après la
relation (2.28).
En notant q le polynôme unitaire
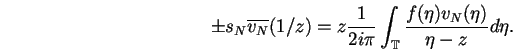 et en évaluant l'expression ci-dessus sur tous les points
et en évaluant l'expression ci-dessus sur tous les points
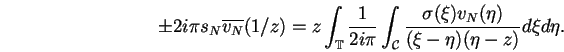 ,
on obtient par combinaison linéaire que
,
on obtient par combinaison linéaire que
 |
(6.32) |
Reste à décomposer notre vecteur singulier vN en facteurs
intérieur/extérieur
![]() pour obtenir une
relation d'orthogonalité analogue à (3.44), soit
pour obtenir une
relation d'orthogonalité analogue à (3.44), soit
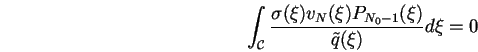 où C est une constante indépendante de n.
où C est une constante indépendante de n.