L'équation d'orthogonalité non hermitienne

Dans ce chapitre, nous présentons des résultats sur le comportement des pôles de nos différents approximants et la manière dont ces informations peuvent être exploitées pour la détection et la localisation de fissures.
Nous montrons dans un premier temps la manière dont la fonction f, (dont on construit une trace sur $\Gamma$ comme décrit dans la section 2.2), peut être décomposée de sorte d'en exhiber la partie singulière sous forme d'une intégrale de Cauchy le long de la fissure $\gamma$.
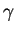Nous montrerons ensuite comment l'approximation de ce type de fonctions par les méthodes décrites précédemment nous ramène à une relation dite ``d'orthogonalité non hermitienne'' sur un contour relié à $\gamma$.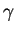
Enfin, nous verrons comment cette relation d'orthogonalité peut nous fournir des informations sur le comportement des pôles de nos approximants par rapport à la position de la fissure.