Pour introduire cette dualité en termes d'analyse complexe, considérons une fonction u satisfaisant le système (1.1) pour un domaine D délimité par une frontière extérieure
Nous entendons par ceci que
D'une manière analogue aux méthodes présentées dans le chapitre
précédent, nous allons utiliser dans notre approche la dualité
entre les données u et ![]() sur le bord
sur le bord ![]() du domaine D.
du domaine D.
Pour introduire cette dualité en termes d'analyse complexe, considérons
une fonction u satisfaisant le système (1.1) pour un domaine
D délimité par une frontière extérieure ![]() Hölder
Hölder
![]() (
(
![]() )
et pour une fissure
)
et pour une fissure ![]() définie
par un arc de Jordan
définie
par un arc de Jordan
![]() incluse dans
incluse dans
![]() et n'intersectant
pas sa frontière extérieure.
et n'intersectant
pas sa frontière extérieure.
Nous entendons par ceci que ![]() admet une paramétrisation de la
forme
admet une paramétrisation de la
forme
![]() telle que
telle que ![]() admette, pour un
admette, pour un
![]() ,
une dérivée Lipschitz d'ordre
,
une dérivée Lipschitz d'ordre ![]() sur
sur
![]() .
.
Cette fonction u est alors harmonique dans
![]() et peut être vue comme étant la partie réelle d'une fonction fanalytique dans
et peut être vue comme étant la partie réelle d'une fonction fanalytique dans ![]() et définie comme
et définie comme
| (5.15) |
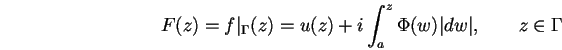 .
.
Connaissant F sur ![]() , trouver un arc de Jordan
, trouver un arc de Jordan
![]() tel
que F soit la trace sur
tel
que F soit la trace sur ![]() d'une fonction f analytique et
bornée dans
d'une fonction f analytique et
bornée dans ![]() .
.
Nous pouvons d'ores et déjà remarquer que cette fonction F dans
Lp est la trace d'une fonction ![]() (p=2 ou
(p=2 ou ![]() )
si et
seulement si la fissure
)
si et
seulement si la fissure ![]() est vide ou confondue avec une ligne
de niveau de f.
est vide ou confondue avec une ligne
de niveau de f.
Une fois la présence d'une fissure établie (en choisissant un
flux identifiant selon la méthode proposée en [28] par
exemple), notre approche réside dans l'étude de différents types
d'approximants de la fonction F sur la frontière extérieure ![]() .
Nous nous intéresserons plus particulièrement aux approximants
rationnels ou méromorphes de F sur la frontière
.
Nous nous intéresserons plus particulièrement aux approximants
rationnels ou méromorphes de F sur la frontière ![]() du
domaine D, et de la façon dont les pôles de ces approximants nous
fournissent une information sur l'existence et la position de la
fissure
du
domaine D, et de la façon dont les pôles de ces approximants nous
fournissent une information sur l'existence et la position de la
fissure ![]() .
.