Analyzing Search Algorithms in Small Worlds
Nicolas Schabanel
Laboratoire d'Informatique Algorithmique: Fondements et Applications (LIAFA), Univ. Paris Diderot, Paris, France.
and Centre National de la Recherche Scientifique (CNRS), Paris, France.
(includes joint work with Emmanuelle Lebhar \& George Giakkoupis)}
The smallworld phenomenon. Milgram revealed in his famous experiment [12] that individuals are not only a few handshakes away from each other, but they are also able to find such short paths between them, in spite of their extremely local view of the worldwide social network. In 2000, Kleinberg [6] proposed a simple random network model that captures this surprising property of social networks. Beyond this natural sociological motivation, his model had an important impact on the design on several peer-to-peer protocols~(e.g., [13]), because it addresses the general question of how decentralized algorithms can find short paths in a partially unknown network.
Kleinberg's model. Kleinberg's small world model consists of a {$d$}-dimensional grid {$\{-n,\ldots, n\}^d$} (representing local acquaintance between individuals, such as geographic or professional) augmented with one "long-range" directed link per node pointing to a random node at distance {$r$} chosen with probability proportional to {$1/r^\alpha$} where {$\alpha$} is a parameter of the model (each long-range link represents a random acquaintance met in the past for instance). Kleinberg defined a decentralized routing algorithm as an algorithm that tries to route locally a message from a node (the source) to another (the target), that is to say, by visiting only neighbors (local or long-range) of already visited nodes (starting from the source). Kleinberg's most striking result is that no decentralized algorithm can find short paths if {$\alpha\neq d$} (i.e., path of length {$polylog(n)$} where {$n$} is the size of the grid), even when the diameter of the augmented graph is {$\Theta(\log n)$} as it was shown later on by [10] [11]}. Only when {$\alpha=d$}, decentralized algorithms may find short paths between random pairs. Indeed, the simple greedy algorithm that simply routes the message to the closest neighbor (local or long-range) of the current message holder computes paths of expected length {$O(\log^2 n)$} [6] (see Fig.1).
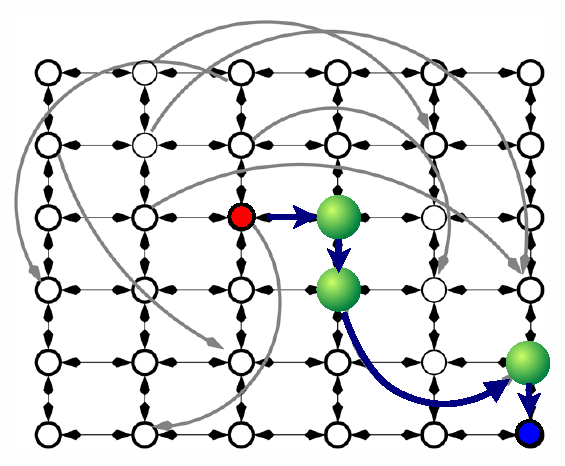
Fig.1: Kleinberg's network and a greedy path from red to blue
Two main types of questions. Kleinberg's model raises two main type of questions. First, from the algorithmic and peer-to-peer network design point of view: Can we beat greedy algorithm? Second, from the sociological point of view: What does this model tell us about real social networks?
- Algorithmic and network design questions. This point is now almost fully understood. Several decentralized algorithms [7] [3] [8] [5] have been proposed that computes much shorter paths to the target than the greedy for the smallworld case when {$\alpha=d$}. [3] proposes a local exploration based algorithm that explores the {$O(\log n)$} closest local neighbors before routing the message: this leads to a path of expected length {$O(\log^{1+1/d}n)$}. [7] [8] [5] propose a non-local exploration based algorithm which explores the {$O(\log^{1+\varepsilon} n)$} closest (in hops) local and non-local contacts before routing the message, which lead to an expected path length of {$\Theta(\log n \log\log n)$} hops when {$d=1$}, and {$\Theta(\log n)$} hops for all {$d\geq 2$}. These two bounds turned out to be optimal: indeed, [5] proves that no efficient decentralized can beat these bounds (even when {$d=1$} where the diameter is {$\Theta(\log n)$}). Note that even if the path computed by these algorithms are much shorter, these algorithms will almost surely visit at least as many nodes as the greedy, {$\Omega(\log^2 n)$} nodes, to compute them as proved by [9].
- Sociological questions. The astonishing algorithm-based result by Kleinberg implies that the so-called \textit{smallworld phenomenon} requires a tight relationship between the long-range contacts randomly collected during life and the underlying topology: {$\alpha=d$}, a relationship that no statistical studies could have spotted. Indeed, this phenomenon is clearly unrelated with diameter (which is polylogarithmic for a much wider range of values: all {${\alpha\in[0,2d]}$} [10] [11]), clustering coefficient (which is close to {$0$} here), or degree distribution (out-degree is uniform, and in-degree follows some Poisson distribution here). This algorithmic approach allows to get a much better understanding of the situation by telling precisely which distribution for the long-range contact is necessary for the smallworld phenomenon to take place.
One important issue is now to explain how this distribution arises in real social networks. Several simple dynamical models have been proposed [2] [1]}. Both of them give raise to the desired long-range link distribution (only experimentally for [2]), but none of them answers completely to the question since they both make some unsatisfying arbitrary choices: the distribution of the "time to forget" for instance in [1]. Another important question is: what kind of algorithm do people use in social network, if any? How can we tell from the experiment?
The three main types of search algorithms. To try to answer these questions, one may want to study the characteristics of the paths constructed by the various algorithms proposed in the literature. These algorithms are essentially of three types: greedy [6], local exploration based [3] and non-local exploration based [7] [8] [5]. Typical paths of each type of algorithm are given in Fig.2, Fig.3, and Fig.4, respectively. One can observed some important differences: the greedy path contains long-range links of all lengths while the two others tend to follow longer long-range links; the local exploration based algorithm tend to follow fewer long-range links than the non-local one and these are much longer. We can observed also some similarities between them: significant progresses toward the target are made by some very long long-range link that happend every so often. This last similarity was indeed proved to be true for every efficient decentralized algorithm: it is a corollary of the proof of the lower bound by [5].
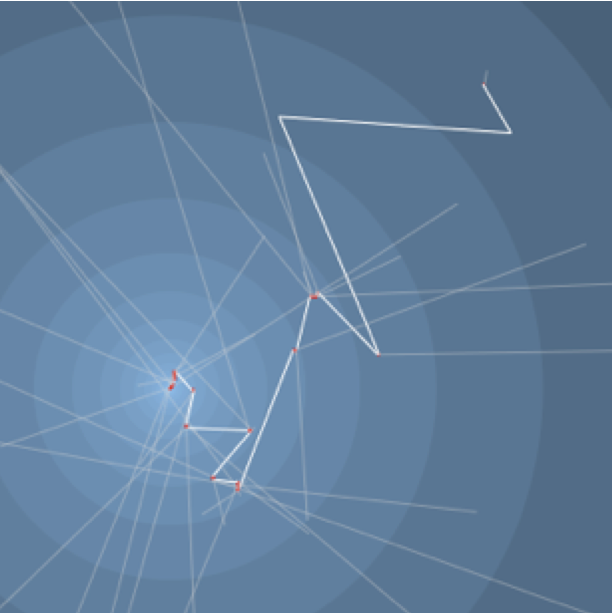
Fig.2: Greedy search algorithm
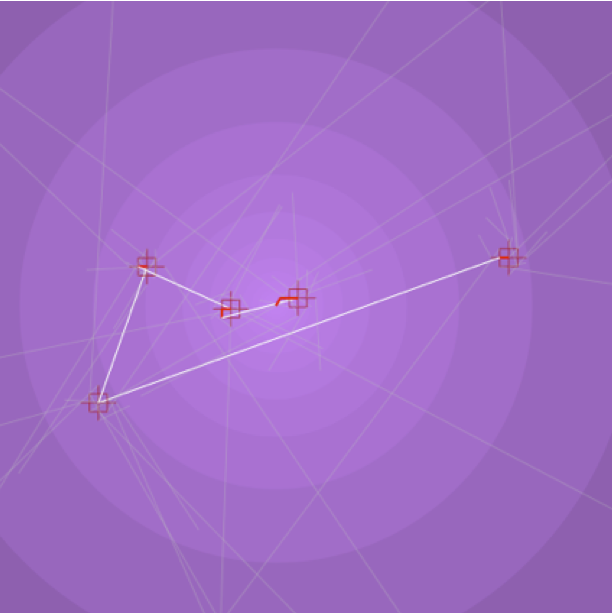
Fig.3: Local exploration search algorithm
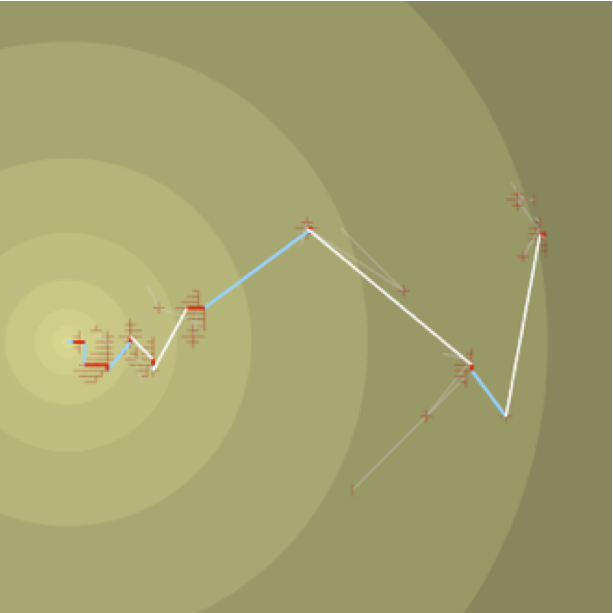
Fig.4: Kleinberg's network and a greedy path from red to blue
Measuring the sociological meaningfulness. In order to find the algorithmic model(s) that best suit the experimental data on the recorded human behaviors in "Milgram-like" experiments, we need to exhibit characteristics of the followed paths that: first, take clearly different values for each type of algorithm; and second, that can easily be computed in the recorded paths from the experiments. With E. Lebhar, we have studied various parameters that could match these two criteria. For instance, Fig.5 displays for the greedy and local exploration based algorithms, the exact "load" of the long-range as a function of their length, i.e., the expected number of paths that go through links of that length given some random source and target. One can observed that the behavior of this parameter differs a lot between the greedy and the local-search algorithms and can also be easily recorded from real-life experiment. At the present time, there is no mathematical of these parameters, but we have some hope that the geometric framework that was designed in [5] (see Fig.6 for an illustration of the key useful facts) should help in that matter.
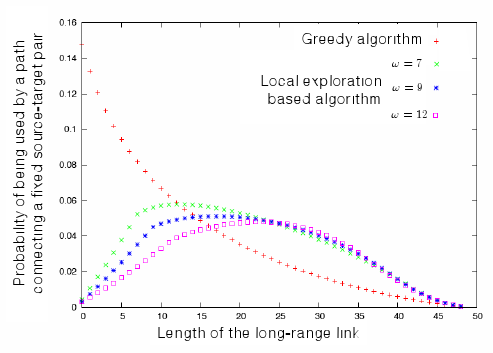
Fig.5: Link load as a function of its length
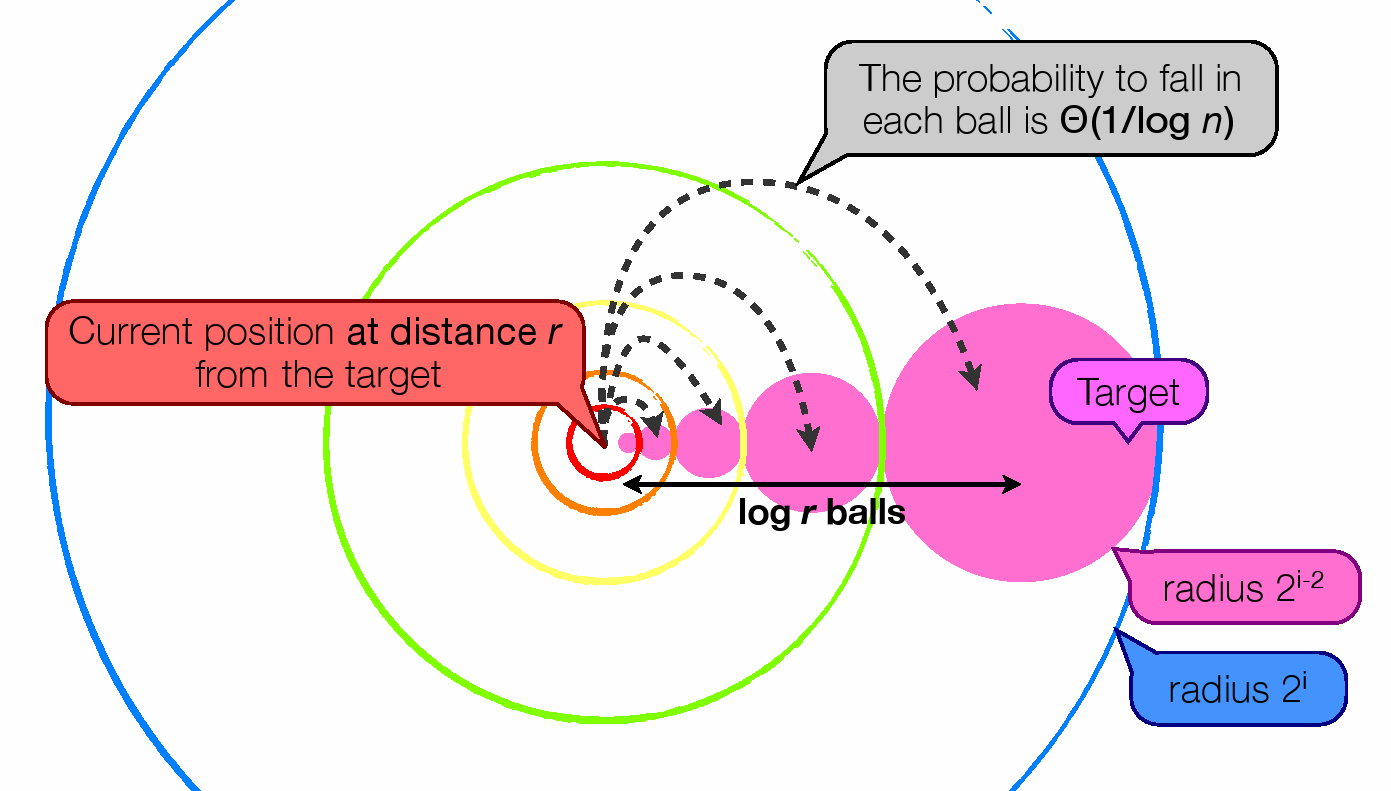
Fig.6: Key geometrical fact for the analysis in [5]
References:
- Augustin Chaintreau, Pierre Fraigniaud, and Emmanuelle Lebhar. Networks become navigable as nodes move and forget. In Proc. of Int. Colloquium on Automata, Languages and Programming (ICALP), LNCS vol.5125, pp.133–144, 2008.
- Aaron Clauset and Christopher Moore. How do networks become navigable ?. textttarxiv.org/abs/0803.0248.
- Pierre Fraigniaud and Cyril Gavoille and Christophe Paul, Eclecticism Shrinks Even Small Worlds, Proc. of ACM Symposium on Principles of Distributed Computing (PODC), pp.169-178, 2004.
- Pierre Fraigniaud and Emmanuelle Lebhar and Zvi Lotker, A Doubling Dimension Threshold {$\Theta(\log\log n)$} for Augmented Graph Navigability, Proc. of European Symposium on Algorithms (ESA), LNCS vol. 4168, pp.376-386, 2006.
- George Giakkoupis and Nicolas Schabanel, Optimal Path Search in Small Worlds: Dimension Matters, Proc. of ACM Symposiul on Theory of Computing (STOC), Vol. 43, pp.393-402, 2011.
- Jon M. Kleinberg, The small-world phenomenon: an algorithmic perspective, Proc. of ACM Symp. on Theory of Computing (STOC), pp.163-170, 2000.
- Emmanuelle Lebhar and Nicolas Schabanel, Almost optimal decentralized routing in long-range contact networks, Proc. of the Int. Colloquium on Automata, Languages and Programming (ICALP), LNCS vol.3142, pp.894-905, July 2004.
- Emmanuelle Lebhar and Nicolas Schabanel. Close to optimal decentralized routing in long-range contact networks. Theoretical Computer Science special issue on ICALP 2004, 348(294-310), 2005.
- Gurmeet Singh Manku, Moni Naor, and Udi Wieder. Know thy neighbor’s neighbor: the power of lookahead in randomized P2P networks. In Proc. of ACM Symposium on Theory of Computing (STOC), 2004.
- Charles Martel and Van Nguyen. Analyzing kleinberg’s (and other) small-world models. In Proc. of ACM Symp. on Principles of Distributed Computing (PODC), pp.179–188, 2004.
- Charles Martel and Van Nguyen. Analyzing and characterizing small-world graphs. In Proc. of ACM/SIAM Symp. On Discrete Algorithms (SODA), pp.311–320, 2005.
- Stanley Milgram. The small world problem. Psych. Today, 2:60–67, 1967.
- Hui Zhang, Ashish Goel, and Ramesh Govindan. Using the small-world model to improve Freenet performance. In Proc. 21st IEEE INFOCOM, pp.1228–1237, 2002.