- Introduction
- Filtering simplification procedures
- The HullConsistency, Simp2B and HullIConsistency procedures
- The HullConsistencyTaylor procedure
- The BiCenteredForm procedure
- The GlobalConsistencyTaylor procedure
- The SimpAngle procedure
- The SimplexConsistency procedure
- The IntervalNewton procedure
- Roots simplification procedures
- Concatenation of simplification procedures
- Using the 3B method
- Simplification procedures for matrix
Simplification procedures
Introduction
For a specific problem the end-user may have some knowledge of the problem that implies that he may determine that for some intervals for the variables the problem has no solution or that the intervals for some variables may be reduced.
ALIAS-Maple allows one to introduce such knowledge in the generated C++ code. The mechanism that is used is to allow one to specify a C++ routine, that will be called a simplification procedure. We will present in this chapter simplification procedures devoted to system solving. A simplification procedure takes as input a set of intervals for the variables and will return an integer:
- -1 if there is no solution to the problem at hand for the given set of intervals
- 1 if the routine has allowed to reduce the width of the intervals of the set
- 0 if the routine has not changed the set of intervals
- 11 if the simplification procedure provides a root that may be found with the Newton scheme (see for example TryNewton)
This routine will be called by all the solving procedure of ALIAS-Maple whenever a new set of intervals is considered in the algorithm i.e. right after the bisection process (see the ALIAS-C++ manual). System solving procedures in ALIAS C++ are designed to discard box for which a simplification procedure returns -1 and to update it if the simplification procedure returns 1.
The syntax of such a routine Simp is:
int Simp(INTERVAL_VECTOR &v_IS)
{
....
return 0;
}
Alternatively ALIAS-Maple allows to automatically produce simplification procedures according to classical methods used in interval analysis.
Note that numerical round-off errors in Maple may produce solving errors as the filtering procedures uses frequently an expanded version of the expressions. To reduce the impact of this problem it is possible to adjust the number of digits that will be used when doing numerical computation in the filtering procedure by using the ALIAS variable `ALIAS/digits` which is set by default to 40.
Filtering simplification procedures
An important point: some of these procedures have as argument a list of variable names and this list must be the same than the one that is used for the solving procedure.
The HullConsistency, Simp2B
and HullIConsistency procedures
The
idea underlying this simplification procedure (known in the community
of constraint programming as the hull-consistency or 2B-consistency)
is to rewrite the
equation and check if it is consistent at each
time. For example imagine that one of the equation is
![]() . The procedure will introduce a new variable
. The procedure will introduce a new variable ![]() such
that
such
that ![]() and compute its interval evaluation. As
and compute its interval evaluation. As ![]() should be
equal to
should be
equal to ![]() if
if ![]() has a negative upper bound the simplification
procedure will return -1, which indicate to the solving algorithm that
it may discard the current input interval. If the upper bound
has a negative upper bound the simplification
procedure will return -1, which indicate to the solving algorithm that
it may discard the current input interval. If the upper bound ![]() of
of ![]() is positive the procedure will check if
is positive the procedure will check if ![]() lie in
lie in
![]() and update the interval for
and update the interval for ![]() if this is not
the case.
if this is not
the case.
In a second step the procedure will introduce another new variable ![]() such that
such that ![]() and compute its interval evaluation. As
and compute its interval evaluation. As ![]() should be equal to
should be equal to ![]() the procedure will check if the interval value
for
the procedure will check if the interval value
for ![]() is consistent with the interval value for
is consistent with the interval value for ![]() and if not
update the interval for
and if not
update the interval for ![]() accordingly.
accordingly.
The HullConsistency and HullIConsistency procedures of
ALIAS-Maple
partly implements this principle respectively for equalities and
inequalities. They may be used if any of the
equation has linear or square terms in the unknown (e.g. ![]() ).
The procedure will isolate the linear and square terms of each unknown
and produce the C++ code that will check is their interval evaluation
is consistent.
).
The procedure will isolate the linear and square terms of each unknown
and produce the C++ code that will check is their interval evaluation
is consistent.
The syntax of the HullConsistency procedure is:
HullConsistency([x^2+y^2-1,x*y-1],[x,y],"Simp");The first argument is a list of equations, the second a list of variable names and the third argument is the name of a file. In the above example the procedure will create the C++ program Simp.C that may be later be given to a solving procedure.
Until version 2.4 was a
HullConsistencyStrong procedure available, that has been contributed by
G. Chabert. The procedure was intended to deal with terms that were
different from linear and square terms that are managed by HullConsistency.
Its drawback was that it was based on a semantic tree of the
expression and was not able to decrease the dependency problem.
For example if the expression is
and the final node is
while HullConsistency will use
which is more efficient. For example in the equation
we will use
to update successively the range for
The new procedure Simp2B manages in a better way the dependency problem but is less
complete than
HullConsistencyStrong, which is no more available for Maple 9.5,
as it manages only the following
expressions
It is also usually more computer intensive than the HullConsistencyStrong procedure. Note that you have some control over the simplification rule that will be used. Consider for example the equation
By default Simp2B will use the following equalities:
ALIAS_FORBIDDEN_TERM:=[e^z]:then only the first and third rule will be used.
The syntax of the HullIConsistency procedure is:
HullIConsistency([x^2+y^2-1<=0,x*y-1<=0],[x,y],0,"Simp");Here the third argument is an integer which should be either 0 or 1. It 1 it indicates that the derivatives of the left side of the inequalities are used for their interval evaluation.
There is an optional last argument to these procedures which is a
floating point number ![]() . If during the simplification there is change in
the interval for a variable such that the width of the new range is
lower by more than
. If during the simplification there is change in
the interval for a variable such that the width of the new range is
lower by more than ![]() from the width of the initial range, then the
simplification process will be repeated until either the procedure
detect that there is no solution to the system or that no change occur
in the variable or that the amplitude of the change is lower than
from the width of the initial range, then the
simplification process will be repeated until either the procedure
detect that there is no solution to the system or that no change occur
in the variable or that the amplitude of the change is lower than ![]() .
.
If you have numerous equations that have such terms the C++ procedure may be quite large. To reduce this size you may choose to look only at the linear term or only at the square term by setting the flag `ALIAS/hullC` to 1 or 2 (its default value is 0). Note that this option is not valid for the HullConsistencyStrong and HullIConsistency procedures.
A typical use of this procedure is given below, assuming that you have a list of equations EQ and a list of variable VAR:
HullConsistency(EQ,VAR,"SS"): HessianSolve(EQ,VAR,Init,"SS");Here the procedure generate the C++ procedure SS (which will be written in the file SS.C) and the solving algorithm HessianSolve will use this procedure during the computation.
The efficiency of the hull consistency approach is usually quite good but decreases quite quickly after the first improvements. Hence it is in general not a good idea to repeat the procedure when only small improvements on the range are obtained.
A test to determine if an expression involved in the equations and inequalities can be interval-valuated may be performed if the Verify_Problem_Expression procedure has been called before the call to HullConsistency or HullIConsistency (see section 2.1.5). If different calls to the consistency procedures are made with different set of expressions it is necessary to specify a different string `ALIAS/ID` string before each call to Verify_Problem_Expression. For example
`ALIAS/ID`:="Simp1": Verify_Problem_Expression(EQ1,VAR): HullIConsistency(EQ1,VAR,"Simp1"): `ALIAS/ID`:="Simp2": Verify_Problem_Expression(EQ2,VAR): HullConsistency(EQ2,VAR,"Simp2"): `ALIAS/ID`:="Simp3": Verify_Problem_Expression(EQ2,VAR): HullConsistencyStrong(EQ3,VAR,"Simp3"): `ALIAS/ID`:="other":is valid.
A special key-word may be used for the procedures HullConsistency and HullIConsistency in the case of an optimization problem. In that case the ALIAS-C++ variable ALIAS_Optimize is set to -1 (minimum problem) or 1 (maximum problem), the flag ALIAS_Has_Optimum is set to 1 as soon as an estimation of the optimum is found while the interval ALIAS_Optimum is set to the estimation of the optimum. If an equation or an inequality has the key-word "Optimum" in it and if ALIAS_Has_Optimum is 1, then "Optimum" will be substituted by Sup(ALIAS_Optimum) (minimum problem) or Inf(ALIAS_Optimum) (maximum problem).
For example assume that you deal with a problem involving the minimum
of
![]() : you may then use the following call
: you may then use the following call
HullIConsistency([x*sin(x)+y*cos(y)-Optimum<=0],[x,y],0,"Simp");to create a simplification procedure that may reduce the current box. See another example in section 5.2
The HullConsistencyTaylor procedure
This procedure uses a third order Taylor extension of an equation and an interval evaluation of the remainder. This leads to a second order equation in each of the variables, whose coefficients is computed. The analytic solution of this second order equation is used to improve the variable range. This filter is very efficient for non algebraic equations and if the width of the range for the variable is not too large.
The syntax is:
HullConsistencyTaylor(func,vars,procname)
An optional fourth argument may be used. It consists in a list of one or two number. If this argument is [0.1,0.01], then the filter will be used only if the maximal width for the ranges is less than 0.1 and the filter will be used again if the gain in a range if larger than 0.01. If only one number is given in the list, then it will indicate the maximal width for the ranges.
The BiCenteredForm procedure
This procedure is based on the interval evaluation of equations using
centered form with as centers two possible centers which may be
optimal (see the ALIAS C++ manual for the calculation of these
centers). The centered form uses the fact the interval evaluation of a
function ![]() in the
in the ![]() unknown
unknown
![]() is included in
is included in
![]() where
where ![]() is point called the center. As mentioned
earlier two possible centers are calculated. Furthermore the
calculation of the product
is point called the center. As mentioned
earlier two possible centers are calculated. Furthermore the
calculation of the product ![]() may involve several occurrences
of the same variables, that are not detected when computing the
product numerically. This procedure allows, as an option, to compute
symbolically the product and to re-arrange it in order to try to
reduce multiple occurrences.
may involve several occurrences
of the same variables, that are not detected when computing the
product numerically. This procedure allows, as an option, to compute
symbolically the product and to re-arrange it in order to try to
reduce multiple occurrences.
The syntax of this procedure is:
BiCenteredForm(func,funcproc,Jfuncproc,vars,custom,procname)where
- func: a list of equations
- funcproc: the name of a procedure in MakeF format that computes the interval evaluation of func
- Jfuncproc :the name of a procedure in MakeJ format that computes the interval evaluation of the derivatives of func
- vars: a list of variable names
- custom: a string that indicate how funcproc and Jfuncproc are obtained.
- "none": the procedure will assume that funcproc and Jfuncproc are the procedures F and J that are generated by GradientSolve and HessianSolve
- "F": the procedure will assume that funcproc is a customized procedure that, for example, has been generated by MakeF
- "J": the procedure will assume that Jfuncproc is a customized procedure that, for example, has been generated by MakeJ
- "FJ": the procedure will assume that funcproc and Jfuncproc are customized procedures
- procname: the name of the simplification procedure that will be created in the file procname.C
The GlobalConsistencyTaylor procedure
This procedure uses a second order Taylor extension of an equation and an interval evaluation of the remainder. The equation system is transformed into a linear part and an interval remainder and an interval linear system solver is used to determine the bounds for the solutions. Hence this filter is global (i.e. it takes into account all equations of a system) while most of the other filter are local (i.e. they deal only with one equation at a time). This filter is usually very efficient for non algebraic equations and if the width of the range for the variable is not too large.
The syntax is:
GlobalConsistencyTaylor(func,vars,procname)
An optional fourth argument may be used. It consists in a list of one or two number. If this argument is [0.1,0.01], then the filter will be used only if the maximal width for the ranges is less than 0.1 and the filter will be used again if the gain in a range if larger than 0.01. If only one number is given in the list, then it will indicate the maximal width for the ranges.
The SimpAngle procedure
This procedure may be used if one of the equation indicates that the
scalar product of two vectors must have some given value. Hence such
equation may be written as:
where the
A typical use of this procedure is given below, assuming that you have a list of equations EQ and a list of variable VAR:
eq1:=(x1-3)*(x2-4)+(y1-1)*(y2-4)-10: SimpAngle([eq1],VAR,"SS"): GeneralSolve(EQ,VAR,Init,"SS"):Here the procedure generate the C++ procedure SS (which will be written in the file SS.C) and the solving algorithm GeneralSolve will use this procedure during the computation.
There is an optional last argument to this procedure which is a
floating point number ![]() . If during the simplification there is change in
the interval for a variable such that the width of the new range is
lower by more than
. If during the simplification there is change in
the interval for a variable such that the width of the new range is
lower by more than ![]() from the width of the initial range, then the
simplification process will be repeated until either the procedure
detect that there is no solution to the system or that no change occur
in the variable or that the amplitude of the change is lower than
from the width of the initial range, then the
simplification process will be repeated until either the procedure
detect that there is no solution to the system or that no change occur
in the variable or that the amplitude of the change is lower than ![]() .
.
The SimplexConsistency procedure
This simplification procedure may be used to solve systems of equations as soon as the system has at least two equations with polynomial terms in at least one variable. The principle used for this simplification procedure is explained in the ALIAS-C++ manual section of Solve_Simplex.
The syntax of this procedure is:
\SimplexConsistency(EQ,VAR,"Simp"):where EQ is a list of equation, VAR a list of variable name and Simp is the name of the simplification procedure that will be written in the file Simp.C.
The behavior of this simplification procedure may be modified by using the following variables:
- `ALIAS/full_simplex`: an integer n. The simplification procedure will try to improve the width of the n largest variable ranges. If n is -1 (the default value for this variable) the procedure will just return -1 if there is no solution to the system but no improvement on the range of the variable will be obtained. n may be larger than the number of variables.
- `ALIAS/diam_simplex`: a floating point number f (default value: 0.1). The procedure will not improve the range of variable whose width is lower than f
- `ALIAS/min_diam_simplex`: a floating point number f (default value: 1e7). The procedure will not try to improve the range of variables whose width is greater than f
- `ALIAS/mid_simplex`: by default the procedure uses a linearization at the lower bound of the variables. If you set this flag to 1, then the linearization point will be the mid point of the range
Two remarks about this procedure:
- it is usually very effective
- it may be computer intensive for large systems: hence its use should in general be avoided within the 3B method (see section 4.5)
- it is not numerically safe with the current implementation of the simplex i.e. in some cases it may lead to miss some solutions
The IntervalNewton procedure
This procedure allows one to take into account the specific structure
of the system to solve when using the interval Newton method. In this
method the classical algorithm, for example used by default in GradientSolve or HessianSolve, computes numerically for a box ![]() the interval evaluation
of
the interval evaluation
of
![]() where
where ![]() is the mid-point of
is the mid-point of ![]() . This
numerical calculation does not allow to to take into account the
dependency between the elements of
. This
numerical calculation does not allow to to take into account the
dependency between the elements of ![]() when computing
when computing ![]() . This
procedure compute symbolically the matrix
. This
procedure compute symbolically the matrix ![]() and re-arrange its
elements (with MinimalCout) in order to reduce the dependency
problem.
and re-arrange its
elements (with MinimalCout) in order to reduce the dependency
problem.
The syntax of this procedure is
IntervalNewton(func,nfunc,funcproc,njfunc,Jfuncproc,typemid,grad,grad3B,incl,vars,procname)where
- func: the list of equations,
- nfunc: the number of equations that will be evaluated by funcproc. It may not be the same than the number of equations in func
- funcproc: the name of the procedure that is used to evaluate the equations. It may be the name of a procedure designed by the end-user with MakeF or the name of the procedure that will be used by the solving algorithm (usually "F")
- njfunc: the number of equations that will be used when computing the derivatives. It may not be the same than the number of equations in func
- Jfuncproc: the name of the procedure that is used to evaluate the derivative of the equations. It may be the name of a procedure designed by the end-user with MakeJ or the name of the procedure that will be used by the solving algorithm (usually "J")
- typemid: the interval Newton method uses a conditioning
matrix. This flag will indicate which type of conditioning matrix is
used. If 0 we use
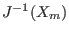 , if 1
, if 1
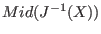 ,
if 2 both above conditioning matrices will be used
,
if 2 both above conditioning matrices will be used
- grad, grad3B: it is possible to use the derivatives of
 to improve the interval evaluation. If grad is set to 1 this
will be used for all boxes in the algorithm. If grad3B is set to
1 it will also be used for the sub-boxes that are considered when
using the 3B method
to improve the interval evaluation. If grad is set to 1 this
will be used for all boxes in the algorithm. If grad3B is set to
1 it will also be used for the sub-boxes that are considered when
using the 3B method
- incl: a list. If the end-user uses a specific procedure to compute the interval evaluation of func, then incl[1] should be set to 1. Similarly if it uses its own procedure to compute the derivatives of func, then incl[2] should be set to 1.
- vars: the list of variables. All
 unknowns in the
unknowns in the 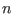 elements of func
must appear first in this list
elements of func
must appear first in this list
- ProcName: the name of the simplification procedure that will be created in the file ProcName.C
Roots simplification procedures
A special type of simplification procedure is the one that are used not for filtering boxes but for finding roots of a system of equations. The general solving algorithm of ALIAS accept such type of procedure that returns 11 if a root is provided by the simplification procedure.
TryNewton
This procedure will create a C++ program that is intended to be used within an equation solving procedure as a simplification procedure. For each call to this program the program will run at most newton_iteration iterations of the classical Newton scheme with as initial guess for the solution the mid-point of the interval vector that is the argument of a simplification procedure. If Newton seems to converge (i.e. the residues have a width lower than fepsilon) the program first checks that the approximation of the root lies within a given search domain and then uses the Kantorovitch theorem and the epsilon-inflation scheme to certify that there is a single solution within a given ball. In that case the program will return 11, otherwise it returns 0. The general use of this procedure is for finding quickly a root of the system although in some cases it may speed up the process of finding all solutions of the system.
The syntax of this procedure is
TryNewton(func,vars,Init,procname)
- func: a list of n equations
- vars: a list of n unknowns names
- Init: a search domain for the solutions
- procname: the name of the simplification program that will be written in the file procname.C
This procedure may be used with GeneralSolve and GradientSolve. It should not be used with HessianSolve as the corresponding C++ program is already embedded in the C++ code of this procedure.
Rouche
The Rouche procedure has to be used for a system of equations
and will create a simplification procedure that may return 11, i.e. it
provide a ball that include a single solution of the system, that may
be found using a Newton iteration.
A key-point for using this procedure is to consider the matrix
constituted of the ![]() -th derivatives of the equations with respect to
the variable, that will be denoted
-th derivatives of the equations with respect to
the variable, that will be denoted ![]() and to be able to find
and to be able to find
![]() such that there is a
such that there is a ![]() in
in ![]()
for all
- algebraic equations
- non-algebraic equations
As soon as there are non algebraic terms in at least one equation, then we cannot determine in advance the order of the Rouche method without an in-depth analysis of the system.
The syntax of this procedure is:
Rouche(Func,nfunc,Order,Vars,ProcName)where
- Func: the list of equations
- nfunc: the number of equations in Func
- Order: the order of the Rouche method. For algebraic equation you may specify "p" for this order as the procedure will determine automatically the correct order. Otherwise it is your responsibility to provide a numerical value for the order
- Vars: a list of variable name
- ProcName: the name of the simplification procedure which will be written in the file ProcName.C
EQ:=[x^2+y^2+z^2-9,(x-1)^2+(y-1)^2+z^2-9,(x-1)^2+(y+1)^2+z^2-16]]: VAR:=[x,y,z]: Rouche(EQ,"p",VAR,"rouche");
This procedure will be called only if the width of the box is lower than ALIAS/maxnewton and uses at most ALIAS/newton_iteration of the Newton scheme to compute an approximation of the root such that the residues of the system are lower than ALIAS/fepsilon. The generated C++ program will also use the epsilon inflation method to enlarge as much as possible the ball that includes the root.
The Rouche procedure may be quite powerful to find a ball that includes a single root of the system (even more powerful than the Kantorovitch scheme). For example by using Rouche in combination with DeflationUP (see section 8.1.2.1) we have been able to solve the Wilkinson polynomial of order 19 (see section 12.3), while the general procedure failed certifying roots starting at order 13.
Concatenation of simplification procedures
In some cases you may have the opportunity to write more than one simplification procedure (for example by using the HullConsistency procedure and writing you own simplification procedure). Currently the procedures in the C++ library and in the Maple library accept only one simplification procedure. But you may concatenate an unlimited number of simplification procedures by using the procedure CatSimp. The first argument of this procedure is the name of the procedure that will be used as unique simplification procedures by ALIAS-C++. The following arguments are names of simplification procedures. Note that the name of the file containing the simplification procedure must always be the name of the procedure with the extension .C. Hence
CatSimp("WholeSimp","Simp1","Simp2")
will produce the file WholeSimp.C defining the procedure WholeSimp which in turn calls the procedures Simp1,Simp2
defined in the file Simp1.C, Simp2.C. Hence the arguments
of the CatSimp procedure are usually strings.
This procedure accepts a numerical value as optional last argument: in that case the whole chain of simplification procedures will be repeated if the width of at least one range has decreased by more than the specified numerical value during the previous run of the simplification procedures.
Some of the simplification procedures may be computer intensive and therefore their use in the 3B method (see section 4.5) may not be recommended. For that purpose it is possible to specify within the CatSimp procedure that a given simplification procedure shall not be used within the 3B method: for that purpose just add the string NO_3B right after the procedure name. Hence:
CatSimp("Simp","Simp1","Simp2","NO_3B"):
will create the simplification procedure Simp that will usually
calls Simp1 and Simp2 except for the 3B method where only
Simp1 will be used.
Using the 3B method
Principle
The 3B method is an usually efficient method to reduce the width of the variable intervals. This method can be used for any algorithm of ALIAS and is embedded in the code of the solving procedures of the C++ library.
The principle of the method is quite simple. Let assume that we deal
with a problem with ![]() variables
variables
![]() and that the range
for the
variable
and that the range
for the
variable ![]() is [
is [![]() ] while
] while ![]() is a small number.
The procedure will examine if the problem may have a solution if the
range for
is a small number.
The procedure will examine if the problem may have a solution if the
range for ![]() is reduced to [
is reduced to [
![]() ]. If it is not the case
the range for
]. If it is not the case
the range for ![]() may be reduced to
[
may be reduced to
[![]() ]=[
]=[
![]() ]. The procedure will then be repeated
by using
]. The procedure will then be repeated
by using ![]() as a new value for
as a new value for ![]() until the algorithm
either determine that there is no solution to the problem or fails to
show that that is no solution for the range [
until the algorithm
either determine that there is no solution to the problem or fails to
show that that is no solution for the range [
![]() ]. The
algorithm will then try to reduce the range for
]. The
algorithm will then try to reduce the range for ![]() on the "right"
side i.e. by examining if the problem has no solution for the range
[
on the "right"
side i.e. by examining if the problem has no solution for the range
[
![]() ]. This process is repeated in turn for each
variable.
]. This process is repeated in turn for each
variable.
Within Maple the value of ![]() is given by the variable
`ALIAS/Delta3B` which set an identical value of
is given by the variable
`ALIAS/Delta3B` which set an identical value of ![]() for
all variables. Alternatively you may specify a specific value of
for
all variables. Alternatively you may specify a specific value of
![]() for each variable by assigning a list to the variable
`ALIAS/Delta3B_ARRAY` with as many elements as unknowns: each
element of this list is the value of
for each variable by assigning a list to the variable
`ALIAS/Delta3B_ARRAY` with as many elements as unknowns: each
element of this list is the value of ![]() for each variable.
for each variable.
The 3B method will not be used for variables whose range have a width greater than a given threshold. This threshold is defined by the variable `ALIAS/Max3B` (default value: 5). You may assign a new value for this threshold by:
`ALIAS/Max3B`:=10:Alternatively you may specify a specific threshold for each variable by using the array `ALIAS/Max3B_ARRAY`. For example:
`ALIAS/Max3B_ARRAY:=array([0.1,0.1,0.05]):indicates that the 3B method will be used only if the width or the input intervals is lower than 0.1 for the 2 first unknowns and 0.005 for the third one.
As soon as the Max3B, Delta3B values have been set you activate
the 3B method by setting the
`ALIAS/3B` variable to 1 or 2.
At iteration ![]() of the 3B method the algorithm will try to
reduce the range for the variable by
of the 3B method the algorithm will try to
reduce the range for the variable by ![]() . Assume that
. Assume that ![]() is
larger than 1 and the algorithm fails:
is
larger than 1 and the algorithm fails:
- if `ALIAS/3B` is set to 1 the algorithm will move to the next variable (or try to reduce the range on the "right" side if we dealing with the "left" side)
- if `ALIAS/3B` is set to 2: the algorithm was considering
for the variable the range [
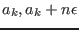 ] when it has
failed. Instead of moving to the next step the algorithm will consider
the range [
] when it has
failed. Instead of moving to the next step the algorithm will consider
the range [
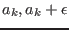 ] and repeat the process until the method
fails for a gain exactly equal to
] and repeat the process until the method
fails for a gain exactly equal to 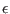
Repeating the 3B method
An improvement may be obtained for the variable ![]() with
with ![]() while
no improvement was obtained for the variable
while
no improvement was obtained for the variable
![]() . But
during the calculation for these variables the range for the variable
. But
during the calculation for these variables the range for the variable
![]() was the initial one and not the improved value. Hence it may be
interesting to repeat the procedure as soon as one the variable is
improved.
was the initial one and not the improved value. Hence it may be
interesting to repeat the procedure as soon as one the variable is
improved.
The 3B procedure will be repeated if:
- the variable
`ALIAS/Full3B`
is set to 1 and the change in at least
one variable is larger than
`ALIAS/Full3B_Change` - the variable `ALIAS/Full3B` is set to 1 or 2 (default value: 0) and if there are two changes on the variable (a change is counted when a variable is changed either on the left or right side) or the change in at least one variable is larger than `ALIAS/Full3B_Change`
The 3B method usually exhibit an asymptotically slow convergence speed and it is hence bad policy of repeating the process for very small improvements in the range.
Other parameters for the 3B method
At one step of the algorithm the 3B method will determine that there is no solution either by considering the simplification procedures provided by the end-user or by a direct evaluation of the expressions involved in the problem.
As the simplification procedures may be computer intensive you may avoid using them within the 3B method by setting the flag `ALIAS/Use_Simp_3B` to 0. Alternatively you may specify that only some of the simplification procedures are to be used within the 3B method by using the mechanism described in the CatSimp procedure (section 4.4). You may also set `ALIAS/Use_Simp_3B` to 2: in that case if some variable ranges have been improved the algorithm will check if the whole improved set of ranges may not be a solution of the problem by using all available simplification procedures (including the one having a "NO_3B" in CatSimp).
As for the interval evaluation of the expressions involved in the problem some of the procedures proposed in ALIAS-Maple may use the derivatives of the expression to improve the interval evaluation. This may be computer intensive and you may avoid using these derivatives within the 3B method by setting the variable `ALIAS/Grad_3B` to a list with as many elements as number of variables. The values in this list are thresholds for the width of the variable ranges such that the derivatives are not used if at least one range width exceed the value.
Simplification procedures for matrix
For some procedure involving matrices there are specific
simplification procedures with a different syntax:
SIMP(int dimA,INTERVAL_MATRIX & A)This procedure shall return -1 if the set of matrices A satisfies a given property, 0 otherwise (dimA is the dimension of the matrices).