- Univariate polynomials
- Parametric polynomial
- Utilities
- Simplification procedures
- Minimal and maximal real roots of a parametric polynomial
- Possible parameters values for a given range for the roots
- Condition number
- Specificity for the analysis of parametric polynomials
Univariate and parametric polynomial
Univariate polynomials
Although Maple can deal efficiently with univariate polynomials we still provide some utilities that may help to design a C++ program to solve and manage univariate polynomial.
Utilities
Bounds for the real roots
The procedure BoundUP allows one to create a C++ program that will determine bounds for the real roots of an univariate polynomial. Its syntax is
BoundUP(Func,Vars,name) BoundUP(x^3-6*x^2+11*x-6,x,"SIMP"); `ALIAS/ID`:="nd": BoundUP(y*x^3-6*x^2+11*x*y-6,[x,y],"SIMP");where
- func: the polynomial
- Vars: the variable name of the polynomial or a list of variable names, whose first element should be the polynomial variable
- name: the name of the created C++ program, that will be written in the file name.C
[AA_low_pos, AA_high_pos] [AA_low_neg, AA_high_neg]that will contain respectively the ranges for the positive and negative real roots of the polynomial. If the program has been able to update the range for the positive roots it will set the global flag AA_Flag[0] to 1 and ALIAS_Flag[1] for the negative roots.
Note that several such procedures may be used as soon as a different `ALIAS/ID` are given between the procedure: if `ALIAS/ID` is not an empty string all global variables AA, ALIAS_Flag will have `ALIAS/ID` appended to their names. Hence in the second above example the lower bound for the positive roots will be AA_low_posnd.
An optional 4th argument may be a list of variable name. In that case
Vars must be a single variable name. This will allow to create
multiple simplification procedures for a parametric polynomial. For
example if ![]() is the polynomial
is the polynomial
then
`ALIAS/ID`:="1": BoundUP(y^3*x^3-6*x^2+11*x*y-6,x,"SIMP1",[x,y]); `ALIAS/ID`:="2": BoundUP(y^3*x^3-6*x^2+11*x*y-6,y,"SIMP2",[x,y]);will create the simplification SIMP1 that consider
Simplification procedures
Deflation
The procedure DeflationUP will create a simplification procedure
based on a re-writting of the univariate polynomial ![]() of degree
of degree ![]() . Let us assume
that approximate roots
. Let us assume
that approximate roots
![]() of the polynomial
of the polynomial ![]() has been
found. Then the polynomial may be written as
has been
found. Then the polynomial may be written as
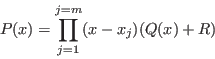
where
The syntax of this procedure is:
DeflationUP(Func,Vars,EvalProc,JevalProc,name)where
- Func: the
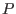 polynomial
polynomial
- Vars: the name of the polynomial variable
- EvalProc: the name of a C++ procedure in MakeF format that will be used to evaluate the polynomial. If GradientSolve or HessianSolve are used as solving procedure this name is by default "F". Otherwise the user may use its own procedure, for example by using MakeF.
- JevalProc: the name of a C++ procedure in MakeJ
format that will be used to
evaluate the derivative of the polynomial. If GradientSolve or HessianSolve
are used as solving procedure this name is by default "J". Otherwise
the user may use its own procedure, for example by using MakeJ.This procedure is used to compute accurately the approximate
roots of
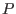 by using the Newton scheme with as initial guess the mid-point of the
global C++ variable
ALIAS_Solution until the residues are lower than `ALIAS/fepsilon`.
Alternatively you may specify "none" for JevalProc in
which case the mid-point of ALIAS_Solution will be used as
approximate solution
by using the Newton scheme with as initial guess the mid-point of the
global C++ variable
ALIAS_Solution until the residues are lower than `ALIAS/fepsilon`.
Alternatively you may specify "none" for JevalProc in
which case the mid-point of ALIAS_Solution will be used as
approximate solution
- name: the name of the simplification procedure that will be written in the file name.C
Parametric polynomial
A parametric polynomial is a polynomial whose coefficients are functions of a set of parameters (in other words it is a set of polynomials).
Utilities
Decomposition
Being given an expression it may be interesting to determine if it can be written as a polynomial in one variable. For example
eq:=x^2*sin(x)+x/sin(y)+ x*exp(x):may be considered as a second order polynomial in
AA1*x^2+AA2*x+AA3*xNote that the coefficients are not collected. while the global variable ALIAS_TERMS will contain the value of the AA. If the returned polynomial has degree 0 in the variable, then the expression is not a polynomial in this variable.
Simplification procedures
Routh table: Routh
The Routh table allows one to determine if all the roots of a polynomial have a negative real part. The number of sign changes in the first column of the table is the number of roots with positive real parts. The Routh table has n+1 rows, where n is the degree of the polynomial.
The syntax of this procedure is:
Routh(poly,Vars,Type,Where,ProcName)where:
- poly is the polynomial
- Vars: a list of variable name whose first element is the polynomial variable
- Type: see below
- Where: if P(x) is the polynomial we will compute the Routh table for P(x+Where). If Where is not 0 the number of sign changes will indicate the number of roots with real part greater than Where.
- ProcName: the name of the simplification procedure
- 0 : the procedure will simply returns the Routh table of the polynomial
 and lower than the degree of the polynomial +1 : the
procedure will create a C++ simplification procedure (whose name is
the last argument of the procedure) that
will compute an interval evaluation of the
and lower than the degree of the polynomial +1 : the
procedure will create a C++ simplification procedure (whose name is
the last argument of the procedure) that
will compute an interval evaluation of the 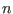 first element of
the first column of the Routh table, using the derivatives of these
elements. This simplification procedure will return -1 if the
polynomial has a root with real part larger than Where. The interval
input of this procedure will be an interval vector corresponding to
Vars. Note that if
first element of
the first column of the Routh table, using the derivatives of these
elements. This simplification procedure will return -1 if the
polynomial has a root with real part larger than Where. The interval
input of this procedure will be an interval vector corresponding to
Vars. Note that if 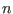 is large the procedure may take a long time
to be generated.
is large the procedure may take a long time
to be generated.
-
![$[k,[n,var1,var2..],[m,var3]]$](img164.png) : if
: if 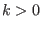 the same
simplification principle
than described in the above section will be generated. Furthermore
we will calculate the sign of the first element of the first row
of the Routh table. If this element has a constant sign (say positive)
we will consider the element at the n-th row of the first column.
Assuming that this element S has a linear term in var1 (S= a var1+b)
with a positive we will write that S is positive when var1
is greater than -b/a and we will update var1
accordingly.
We will proceed similarly with the element at of row m and with
variable var3
the same
simplification principle
than described in the above section will be generated. Furthermore
we will calculate the sign of the first element of the first row
of the Routh table. If this element has a constant sign (say positive)
we will consider the element at the n-th row of the first column.
Assuming that this element S has a linear term in var1 (S= a var1+b)
with a positive we will write that S is positive when var1
is greater than -b/a and we will update var1
accordingly.
We will proceed similarly with the element at of row m and with
variable var3
Routh(x1+(x1+x2)*s+x2^2*s^2,[s,x1,x2],0,0);
[ 2 ]
[ x2 x1 0]
[ ]
[x1 + x2 0 0]
[ ]
[ x1 0 0]
The first element of the Routh table is positive and
the second element of the first row is Routh(x1+(x1+x2)*s+x2^2*s^2,[s,x1,x2],[2,[2,x1,x2]],0,"ROUTH");will imply that the simplification procedure will use the simplification rules
The KharitonovConsistency procedure
This procedure may be used when dealing with the problem of determining if the roots of a parametric polynomial all lie within a given range.
For a parametric polynomial there is usually four Kharitonov polynomials i.e. polynomials have that have constant coefficients. It can be shown that if all the Kharitonov polynomials have the real parts of their roots of the same sign, then all the polynomials in the set will have the real part of their of the same sign. The following procedure allows to use the Kharitonov polynomials to test if there they may be roots of a parametric polynomial within a given range. Its syntax is:
KharitonovConsistency(Func,Vars,Gradient,procname)with the following parameters:
- Func: a polynomial. If Func is a matrix, then the polynomial is supposed to be the characteristic polynomial of the matrix
- Vars: list of unknowns. The first one must be the unknown of the polynomial. If Func is a matrix the first name must be AXX
- Gradient: a flag that indicates if the derivatives of the polynomial with respect to the unknowns may be used (1) or not (0)
- procname: the name of the simplification procedure. The name of the created file will be procname.C
The WeylFilter procedure
Let ![]() be a polynomial and be maxroot the maximal modulus of
the root of
be a polynomial and be maxroot the maximal modulus of
the root of ![]() . From
. From ![]() we may derive a the unitary polynomial
we may derive a the unitary polynomial ![]() such that the
roots of
such that the
roots of ![]() have a modulus lower or equal to 1 and if
have a modulus lower or equal to 1 and if ![]() is a root
of
is a root
of ![]() then maxroot
then maxroot![]() is a root of
is a root of ![]() .
.
Let
![]() which may also be written as
which may also be written as
![]() where
where ![]() is some fixed point.
is some fixed point.
Let a range ![]() for
for ![]() and let
and let ![]() be the mid point of the
range. We consider the square in the complex plane centered at
be the mid point of the
range. We consider the square in the complex plane centered at ![]() and whose edge length is
and whose edge length is ![]() . Let
. Let ![]() be the length of the
half-diagonal of this square.
If
be the length of the
half-diagonal of this square.
If
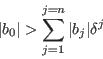
then the polynomial has no root in the square. For a given list of equations we consider in turn each equation and determine if it may be considered as a parametric polynomial. For example the equation
WeylFilter(Func,Vars,FullVars,MaxRoot,TypeB,name)will consider each equation in the list Func and examine if it may considered as a parametric polynomial successively in each variable in the list Vars. If yes the Weyl filter will be used on the polynomial whose coefficients are functions of the variables in the list FullVars (all variables in Vars must be a member of FullVars). MaxRoot is a list which indicates for each variable in Vars what is the maximum modulus of the roots of all parametric polynomials in this variable. An element of MaxRoot may be a numerical value of the key-word "automatic" which indicates that the C++ program will try to determine the maximal modulus. The list TypeB indicates for each variable in Vars how are computed the
WeylFilter([x^2*sin(x)+x*sin(y)+ x*exp(x)],[x],[x,y],["automatic"],["symbolic"],"SIMP");Another example of the use of this procedure is presented in section 12.3.
Minimal and maximal real roots of a parametric polynomial
The basic procedures for computing the minimal and maximal roots of a parametric polynomial are:
MinMax_Polynom(Func,Vars,Init,Type,Solve,Rand,Points,Min,Pm,Max,PM) MinMax_Polynom_Gradient(Func,Vars,Init,Type,Solve,Rand,Points,Min,Pm,Max,PM)where
- Func: the list of constraints between the parameters and polynomial unknown. The polynomial must be the last element of this list. If this last element is a matrix then the considered polynomial is the characteristic polynomial of the matrix (but this is not the more efficient procedure for this case, see next section). If this last argument is Fast_CharPoly(S),Medium_CharPoly(S) or Slow_CharPoly(S) where S is a matrix the polynomial is the characteristic polynomial of the matrix but this polynomial will not be computed by Maple. Instead the procedure Coeff_CharPoly will be used to compute the coefficients of the polynomial: this may be interesting for relatively large matrix.
- Vars:a list giving the name of the unknown starting with the name of the polynomial unknown
- Init: a list of ranges for the unknown starting with the range for the polynomial unknown (this element should be set to a large interval and is updated automatically) followed by the ranges for the parameters
- Type: 0 to find only the minimal root, 1 to find only the maximal root and 2 to find both.
- Solve: a flag that should usually be set to 3, see the on-line help
- Rand, Points: the equivalent of the rand and
Nb_Points arguments of the C++ procedure
ALIAS_Min_Max_EigenValues, see the ALIAS-C++ manual - Min, Max: minimum and maximum root
- Pm,PM: values of the parameters at which the minimum and maximum have been obtained
The difference between these two procedures is that the second one uses the derivatives of the polynomial with respect to the variables together with the derivative of the coefficients of the polynomial.
For these procedures the flag `ALIAS/stop_opt_sol`, `ALIAS/opt_sol_max` will play the same role than Stop, Seuil[0] and Seuil[1] of the C++ procedure ALIAS_Min_Max_EigenValues, see the ALIAS-C++ reference manual.
In the special case where the polynomial is the characteristic polynomial it may be interesting to use the specific procedures:
MinMax_Char_Poly(Func,Vars,Init,Type,Solve,Rand,Points,Min,Pm,Max,PM) MinMax_Char_Poly_Gradient(Func,Vars,Init,Type,Solve,Rand,Points,Min,Pm,Max,PM)which has the same argument that the previous procedures except that the last argument of Func must be a matrix.
Possible parameters values for a given range for the roots
It is possible to determine an approximation of the region of the
parameters space (a ![]() dimensional space
where each of the dimension corresponds to one of the
dimensional space
where each of the dimension corresponds to one of the ![]() parameters)
that contain all the possible values of the
parameters such that the corresponding polynomial has all its roots in
a given range. This approximation will be constituted of a set of
parameters)
that contain all the possible values of the
parameters such that the corresponding polynomial has all its roots in
a given range. This approximation will be constituted of a set of ![]() dimensional boxes written in a file. The procedure to be used is:
dimensional boxes written in a file. The procedure to be used is:
MinMax_Polynom_Area(Func,Vars,Init,Strong,Solve,Rand,Points,Out,Lim,Type)where
- Out: a string which is the name of the file in which the result will be written
- Lim: during the calculation all the boxes that have a width lower than this value will be neglected
- Type: a string that may be "Real" (if only the real root or the polynomial are considered), "RealPart" (for the real part of the root), "AllReal" (for polynomial having only real root), "OneReal" (for polynomial having at least one real root)
Strong is a list of two elements: the first element may be 1 or 2. If it is 2 the derivative of the coefficients of the polynomial will be used. This algorithm uses a secondary bisection process and the second element of Strong gives the maximum number of boxes that can be used for the secondary algorithm.
The range for the real roots of the polynomial is defined as:
[`ALIAS/opt_sol_min`,`ALIAS/opt_sol_max`]It is possible to improve incrementally the quality of the approximation. During the first run the flag `ALIAS/ND` will be set to 1 and the neglected boxes will be written in the file `ALIAS/ND_file`. During the next run Lim has to decreased and the flag `ALIAS/ND` has to be set to 2. This has the effect that the initial box considered by the algorithm will not be Init but the set of boxes stored in `ALIAS/ND_file`. In this run the neglected boxes will still be stored in the file, thereby allowing another run of the algorithm with a lower Lim.
The largest square enclosed in the parameters space such that the polynomials defined by parameter values within the square have all their real roots within a given range can be computed using:
MinMax_Square_Polynom_Gradient(Func,Grad,Vars,Range,Init,Rand,Points,Center,Edge)where Center will be the center of the largest square while Edge will be the lengths of the edge of the square. If you have imperative constraint you may use the variable `ALIAS/Imperatif` as a list with 0 for non imperative constraints and 1 for imperative constraints. Note that this algorithm uses a main algorithm for getting the largest square and a secondary algorithm for calculating the minimal and maximal root of the polynomial in a given square. You may specify two different bisection mode, one for the main algorithm (`ALIAS/single_bisectiong`) and one for for the secondary algorithm (`ALIAS/single_bisection). Similarly the maximal number of boxes used by the main algorithm may be specified by `ALIAS/maxboxg` while the number of boxes used by the secondary algorithm is specified by `ALIAS/maxbox`
Condition number
The condition number of a polynomial may be defined either
as the ratio lowest root over largest root or as the ratio
![]() over
over
![]() where
where ![]() are the roots of the
polynomial. In the later case the condition number has a value between
0 and 1.
The minimal and maximal values of the condition number of a parametric
polynomial in both form may be calculated using the procedure:
are the roots of the
polynomial. In the later case the condition number has a value between
0 and 1.
The minimal and maximal values of the condition number of a parametric
polynomial in both form may be calculated using the procedure:
MinMax_Condition_Number_Gradient(Func,Vars,Init,Type,Absolute,Rand,Min,Pm,Max,PM)where Absolute has to be set to 0 if looking for the ratio minimal root over maximal root or 1 if looking for the ratio in absolute value. The parametric polynomial should appear as last argument of Func. Note that is this last element is a matrix then the considered polynomial will be the characteristic polynomial of the matrix. This procedure may hence be used to compute the minimal and maximal value of the condition number of a matrix. Note here that the derivatives of the polynomial and of its coefficients must be available.
Specificity for the analysis of parametric
polynomials
The following variables play a role in the procedures involving a parametric polynomial:
- `ALIAS/opt_min`, `ALIAS/opt_max`: initial value for the minimum and maximum real roots of a parametric polynomial
- `ALIAS/stop_opt_sol`: if set to 1 the algorithm will
exit soon as a maximum greater than
`ALIAS/opt_sol_max` or a minimum lower than `ALIAS/opt_sol_min` has been found. If set to 2 while looking for a minimum and a maximum the algorithm will exit if both the minimum is lower than `ALIAS/opt_sol_min` and the maximum is greater than `ALIAS/opt_sol_max`
- the variable `ALIAS/user_CoeffINIT` allows to define auxiliary variable in the C++ procedure that implement the evaluation of the coefficients of the polynomial
- a procedure ALIAS_Coeff(fid,i) may be created that determine if the coefficient i may be evaluated and if not affect to him an arbitrary large value.
To create the procedure ALIAS_Coeff we may also use the Problem_Expression package (see section 2.1.5). The procedure ALIAS_Coeff will be obtained from a list of coefficients Coeff in the variable Vars with the following maple code:
`ALIAS/low_value_expr_violated`:= -1e20; `ALIAS/high_value_expr_violated`:= 1e20; Verify_Problem_Expression(Coeff,Vars,"ALIAS_Coeff","ALIAS_Coeff");
Finally the above procedures may use the simplification procedure BoundUP, see section 8.1.1.1, that uses general roots bound algorithms for determining if a polynomial may have a root within a given interval.