Continuation for one dimensional system
Although mostly devoted to zero-dimensional systems ALIAS still
offers some possibilities to deal with
Continuation 1D
Mathematical background
Let consider a system ofThis method enable to follow all the branches for which initial points have been found when solving the initial system. We may then store these points in an array, for example at regular step for the value of the parameter.
By default we use Kantorovitch theorem to follow the branches but by
setting the global variable
ALIAS_Use_Kraw_Continuation
to 1 we will use Moore test.
Implementation
Certified Newton
The procedure that allow to determine the next point on a branch is implemented as:
int Certified_Newton(int Nb_Var,int Dimension_Eq,int Nb_Branch,int Branch,
INTERVAL_VECTOR (* Func)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Gradient)(int, int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Hessian)(int, int, INTERVAL_VECTOR &),
double Accuracy_Var,double Accuracy,
double *param,double delta_param,double min_delta_param,
int sens,MATRIX &Solution)
This procedure determine if it possible to find a new point on the
branch numbered Branch among the Nb_Branch that have been
found. In Solution we have all the solutions that have been
found for the branches when the parameter value was param. The
change in the parameter value will be at most sensThis procedure returns:
- -1, -4: even with a change of the parameter value of min_delta_param we cannot either distinguish two solutions or Kantorovitch has failed to give a positive answer. But this does not mean in general that a singularity occurs.
- -2: for systems having more equations than unknowns the solution that has been obtained with Newton for the square system of equations failed to cancel the remaining equations
- -3: Newton has not converged (should not occur)
- -10: singular point
- 1, 2: procedure has succeeded
Procedure for following branches
This procedure takes as input a set of ![]() solutions of the system and
will return points on the
solutions of the system and
will return points on the ![]() branches. The branches will be followed
until a given value for the parameter is reached or if Kantorovitch
theorem is no more satisfied for some value of the parameter.
It is implemented as:
branches. The branches will be followed
until a given value for the parameter is reached or if Kantorovitch
theorem is no more satisfied for some value of the parameter.
It is implemented as:
int ALIAS_Start_Continuation(int m,int n,int NUM,
INTERVAL_MATRIX &Solutions,
INTERVAL_VECTOR (* IntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Gradient)(int, int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* IntervalHessian)(int,int,INTERVAL_VECTOR &),
double epsilon,double epsilonf,
double *z,double delta,double mindelta,
INTERVAL &Rangez,
int sens,
MATRIX &BRANCH,int *NBBRANCH)
the arguments being:
- m: number of unknowns
- n: number of equations
- NUM: the number of solutions of the system for the current value of the parameter z
- Solutions: the solutions of the system for the current value of the parameter z
- IntervalFunction: a function which return the interval vector evaluation of the equations, see note 2.3.4.3.
- IntervalGradient: a function which return the interval matrix of the jacobian of the equations, see note 2.4.2.2
- IntervalHessian: a function which return the interval matrix of the Hessian of the equations, see note 2.5.2.1
- epsilon: the maximal width of the box, see the note 2.3.4.6. If all the variable ranges have a width lower than this value and the interval evaluation of the equations contains all 0, then the set of ranges is considered to be a solution. But they will be not considered as a valid solution as they will not satisfy Kantorovitch theorem. Hence you must put here a very small value
- epsilonf: the maximal width of the equation intervals, see the note 2.3.4.6. This value will be used by the iterative Newton scheme to stop the iteration.
- z: the parameter of the system
- delta: if
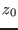 is the first value of the parameter such
that the system has solutions, then we will store in BRANCH the
solutions for
is the first value of the parameter such
that the system has solutions, then we will store in BRANCH the
solutions for 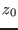 +delta,
+delta, 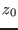 +2delta,...
+2delta,...
- mindelta: if the algorithm is unable to find a Kantorovitch solution for the parameter value z+mindelta while a solution has been found for z, then the algorithm will assume that we are close to a singular point. Hence mindelta should have a small value
- Rangez: the range for the parameter z
- sens: either 1 or -1. If 1 the branch will be computed for increasing values of z, if -1 for decreasing values of z. This parameter should be chosen according to the largest number of solutions of the system for the lower and upper value of z
- BRANCH: the procedure will return an array of NBBRANCH lines and m+2 columns, which describe the points of the branch. In a line the first m+1 elements are the coordinates of the point and the m+2 elements is the number of the branch to which belong this point. The points are not ordered with respect to the branch number. The algorithm will take care of resizing BRANCH as needed, hence there is no need to give dimension for this parameter
- NBBRANCH: the total number of points in the array BRANCH.
- 1: the branches have been successfully determined
- -1, -2: the algorithm has failed to find a Kantorovitch solution for the current value of the parameter
- -3: failure in Newton method (should not occur)
- -10: for the current value of the parameter the jacobian is singular
- -20: sens is not 1 or -1
- -30: delta or mindelta is negative
Full continuation procedure
This procedure will determine initial points on the branches of the
system for the value
of the parameter within some bounds and then follow the branches. It
is implemented as
int ALIAS_Full_Continuation(int m,int n,
INTERVAL_VECTOR (* IntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Gradient)(int, int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* IntervalHessian)(int,int,INTERVAL_VECTOR &),
INTERVAL_VECTOR &Domain,
int M,
double epsilon,double epsilonf,
double *z,double delta,double mindelta,double mindz,
INTERVAL &Rangez,
int sens,
MATRIX &BRANCH,int *NBBRANCH)
The arguments are the same than for the previous procedure except for:
- Domain: the range for the m variable in which we will look for solutions of the system,
- M is the maximum number of boxes which may be stored (see the note 2.3.4.5)
- mindz: the accuracy
with which the starting point for the branches will be determined: if
the value of the parameter at which the branches will start is
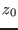 ,
then the system has no solution for
,
then the system has no solution for 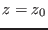 -mindz. This is done
by using a bisection on the parameter: if at
-mindz. This is done
by using a bisection on the parameter: if at 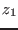 the system has no
solution and has a positive number of solution at
the system has no
solution and has a positive number of solution at 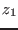 +delta,
then we will solve the system for
+delta,
then we will solve the system for 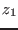 +delta/2. At each time we
will store the value
+delta/2. At each time we
will store the value 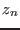 of the parameter for which there is no solution
of the system and the value
of the parameter for which there is no solution
of the system and the value 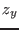 for which we have solutions and we
will stop the bisection on the parameter as soon as
for which we have solutions and we
will stop the bisection on the parameter as soon as 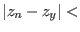 mindz.
mindz.
There is also another version of this program where you indicate just before Domain the solutions which have already been found. The syntax is
INTERVAL_MATRIX (* IntervalHessian)(int,int,INTERVAL_VECTOR &),
int NUM,
INTERVAL_MATRIX &Solutions,
INTERVAL_VECTOR &Domain
The return code for these procedures are:
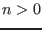 : the number of branches found by the algorithm
: the number of branches found by the algorithm
- -1: no initial point have been found
- -10: Newton algorithm has failed (should not occur)
- -20: sens is not 1 or -1
- -30: delta or mindelta is negative
Finding the initial starting point with the accuracy
mindz may be computer intensive.
Hence the integer global variable
ALIAS_Allow_Backtrack
enable to disable this process if it is set to 0 (its default value is
1): in that case as soon as starting points have been found (hence at
![]() +
+ ![]() delta) we will start following the branches.
delta) we will start following the branches.
In fact these procedures are special occurrences of another ALIAS
procedure which has another argument right after the Hessian
argument. Assume for example that you are considering a system which
has one equation written as:
where
INTERVAL_VECTOR Range(double z, INTERVAL_VECTOR &Variable)where z is parameter value and Variable the current set of ranges for the unknowns. This procedure must return a set of ranges for the unknowns (be careful to check that the returned ranges are included in the initial ranges).
Note also that the ALIAS-Maple package offers a procedure that uses the method described in section 2.14 for finding the initial starting points of the branches: this method is efficient if the equations include linear terms in the unknowns.
Missed branches
Clearly there is a major problem with the method we are proposing: we
may miss some branches. For example imagine that a system has ![]() roots for the initial value of the parameter, but will have more than
roots for the initial value of the parameter, but will have more than
![]() solutions for another value of the parameter, meaning that
new branches appear: our algorithm will find only the
solutions for another value of the parameter, meaning that
new branches appear: our algorithm will find only the ![]() initial
branches. There are two methods that can be used to find the correct
number of branches. The first one is simply to start following the
branches with as initial value for the parameter the one among the
highest or smallest value having led to the maximum number of
solution.
There is also another mechanism that enable to avoid missing
branches. Assume that the solving procedure has determined for some
initial value
initial
branches. There are two methods that can be used to find the correct
number of branches. The first one is simply to start following the
branches with as initial value for the parameter the one among the
highest or smallest value having led to the maximum number of
solution.
There is also another mechanism that enable to avoid missing
branches. Assume that the solving procedure has determined for some
initial value ![]() of the parameter
of the parameter
![]() solutions to the system and that at some point
solutions to the system and that at some point ![]() the continuation
method has failed: the solving procedure is called and determine that
the system has now
the continuation
method has failed: the solving procedure is called and determine that
the system has now ![]() solutions. This mean that for some parameter
value between
solutions. This mean that for some parameter
value between ![]() and
and ![]() we have missed
we have missed ![]() branches. At such point, called problem point it would be
interesting to backtrack i.e. to start again a continuation process
with as initial point for the branches the
branches. At such point, called problem point it would be
interesting to backtrack i.e. to start again a continuation process
with as initial point for the branches the ![]() solutions obtained for
solutions obtained for
![]() and a value for Sens which
is the opposite of the initial value. This is what
is done by the procedure which may store up to 10 problem points. As
this process may be computer intensive it is possible to disable it by
setting
the integer global variable
ALIAS_Problem_Continuation to -1 (it's default value is 0,
which mean that the process is enabled).
and a value for Sens which
is the opposite of the initial value. This is what
is done by the procedure which may store up to 10 problem points. As
this process may be computer intensive it is possible to disable it by
setting
the integer global variable
ALIAS_Problem_Continuation to -1 (it's default value is 0,
which mean that the process is enabled).
Example
Let consider the system: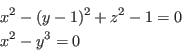
The purpose of this example is to write the points of the branches of this system in files whose name is BRANCH followed by the branch number. The main file is written as:
#include "Functions.h"
#include "Vector.h"
#include "IntervalVector.h"
#include "IntervalMatrix.h"
#include "IntegerMatrix.h"
#include "header_Solve_General_Interval.h"
#include "header_Utilities_Interval.h"
double z;
//F,J,H are the equation, jacobian and hessian procedures
#include "F.C"
#include "J.C"
#include "H.C"
int main()
{
MATRIX BRANCH;
INTERVAL RANGE;
int NUM,i,j,NB_BRANCH;
char texte[400];
double delta=0.05;
double min_delta=1.e-6;
double mindz=1.e-4;
ostream out;
int Nb_Var=2;
int Nb_Eq=2;
Domain(1)=INTERVAL(-100,100);
Domain(2)=INTERVAL(-100,100);
RANGE=INTERVAL(0.2);
NUM=ALIAS_Full_Continuation(Nb_Var,Nb_Eq,F,J,H,Domain,1.e-6,1.e-6,&z,
delta,min_delta,mindz,RANGE,1,BRANCH,&NB_BRANCH);
//order the branch and write the result in the file
for(i =1;i<=NUM;i++)
{
sprintf(texte,"BRANCH%d",i);
out.open(texte,ios::out);
for(j =1;j<=NB_BRANCH;j++)
{
if(BRANCH(j,Nb_Var+2)!=i)continue;
out<<BRANCH(j,1)<<" "<<BRANCH(j,2)<<" "<<BRANCH(j,3)<<endl;
}
out.close();
}
}