La page de J-P. Merlet

J-P. Merlet home page

La page Présentation de HEPHAISTOS

HEPHAISTOS home page

La page "Présentation" de l'INRIA

INRIA home page

Subsections

• Definite integrals
  • Integral with one variable
  • Integral with multiple variable

Integration

Definite integrals

ALIAS offers various procedures to determine bounds for the value of definite integrals with one or more variables. Some of them involve the use of the derivatives and you should be careful when the interval evaluation of these derivative cannot be performed. For example when considering $e^x+2\sqrt{x}+1$ you should not 0 in the integration domain. In that case you should integrate around 0 by using the Integrate problem while using another procedure for the remaining part of the domain.

Integral with one variable

 
int Integrate(
	      INTERVAL_VECTOR (* TheIntervalFunction)
	      (int,int,INTERVAL_VECTOR &), 
	      INTERVAL & TheDomain, 
	      int Iteration,
	      double Accuracy,
	      INTERVAL & Result)

The simplest integration procedure of ALIAS that should be used only for the simplest function.

• TheIntervalFunction: a procedure in MakeF format to interval evaluate the function
• TheDomain: integration domain
• Iteration: this procedure uses a set of boxes and Iteration is the maximum number of boxes that can be used
• Accuracy: desired accuracy for the integration: the width of the result should be lower than this number
• Result: the range for the integral

This procedure returns 1 if the calculation has been successful, -1 if the desired accuracy cannot be reached and -2 if the number of boxes has been exceeded.

If the function is at least twice differentiable it is possible to use:

 
int IntegrateTrapeze(
          INTERVAL_VECTOR (* TheIntervalFunction)
          (int,int,INTERVAL_VECTOR &), 
          INTERVAL_VECTOR (* SecondDerivative)
          (int,int,INTERVAL_VECTOR &), 
          INTERVAL & TheDomain, 
          int Iteration,
          double Accuracy,
          INTERVAL & Result)

int IntegrateRectangle(
          INTERVAL_VECTOR (* TheIntervalFunction)
          (int,int,INTERVAL_VECTOR &), 
          INTERVAL_VECTOR (* SecondDerivative)
          (int,int,INTERVAL_VECTOR &), 
          INTERVAL & TheDomain, 
          int Iteration,
          double Accuracy,
          INTERVAL & Result)

The procedure SecondDerivative in MakeF format allows to interval evaluate the second derivative of the function.

Alternatively it is possible to use:

 
int IntegrateTaylor(
          INTERVAL_VECTOR (* CoeffTaylor)
          (int,int,INTERVAL_VECTOR &), 
          int Order,
          INTERVAL & TheDomain, 
          int Iteration,
          double Accuracy,
          INTERVAL & Result)

The procedure CoeffTaylor, in MakeF format, should provide the interval evaluation of the Taylor coefficients of the function up to the order Order+1 (i.e. Order+2) coefficients).

Integral with multiple variable

ALIAS offers 4 procedures to compute definite integral with more than one variable.

 
int IntegrateMultiRectangle(
          INTERVAL_VECTOR (* Function)
          (int,int,INTERVAL_VECTOR &), 
          INTERVAL_VECTOR (* Second_Derivative)
          (int,int,INTERVAL_VECTOR &), 
          INTERVAL_VECTOR & TheDomain, 
          int Iteration,
          double Accuracy,
          INTERVAL & Result)

int IntegrateMultiRectangle(
          INTERVAL_VECTOR (* Function)
          (int,int,INTERVAL_VECTOR &), 
          INTERVAL_VECTOR (* Second_Derivative)
          (int,int,INTERVAL_VECTOR &), 
          INTERVAL_MATRIX (* Gradient)(int, int,INTERVAL_VECTOR &),
          INTERVAL_VECTOR & TheDomain, 
          int Iteration,
          double Accuracy,
          INTERVAL & Result)

In the second form Gradient is a procedure in MakeJ format that allows to compute the derivatives of the second derivatives of the function. ALIAS offer also procedure based on Taylor expansion of the function.

 
int IntegrateMultiTaylor(
          INTERVAL_VECTOR (* CoeffInt)
          (int,int,INTERVAL_VECTOR &), 
          INTERVAL_VECTOR (* RestTaylor)
          (int,int,INTERVAL_VECTOR &), 
          INTEGER_MATRIX &APOWERINT,
          INTEGER_MATRIX &APOWERREM,
          int nbrem,
          int Order,
          INTERVAL_VECTOR & TheDomain, 
          int Iteration,
          double Accuracy,
          INTERVAL & Result)
int IntegrateMultiTaylor(
          INTERVAL_VECTOR (* CoeffInt)
          (int,int,INTERVAL_VECTOR &), 
          INTERVAL_VECTOR (* RestTaylor)
          (int,int,INTERVAL_VECTOR &), 
          INTEGER_MATRIX &APOWERINT,
          int Order,
          INTERVAL_VECTOR & TheDomain, 
          int Iteration,
          double Accuracy,
          INTERVAL & Result)

The Taylor expansion of the function $F$ may be written as:

$$F(x_1,\ldots,x_n)=\sum C_{i_1i_2\ldots i_n} (x_1-h_1)^{i_1}(x_2-h_2)^{i_2}\ldots(x_n-h_n)^{i_n} +R$$

• CoeffInt: a procedure in MakeF format that compute the coefficients $C_{i_1i_2\ldots i_n}$
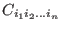
• APOWERINT: a table with the exponent 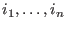$i_1,\ldots, i_n$ for each term
• RestTaylor, APOWERREM: in the first form they play the same role than CoeffInt, APOWERINT for the remainder. There is nbrem terms in the remainder
• RestTaylor: in the second form a procedure in MakeF format that compute the remainder
• Order: the degree of the remainder

J-P. Merlet home page

La page Présentation de HEPHAISTOS

HEPHAISTOS home page

La page "Présentation" de l'INRIA

INRIA home page