Next: Troubleshooting: ALIAS does not Up: ALIAS-C++ Previous: How to install ALIAS

La page de J-P. Merlet

J-P. Merlet home page

La page Présentation de HEPHAISTOS

HEPHAISTOS home page

La page "Présentation" de l'INRIA

INRIA home page

Subsections

Examples of application of `ALIAS-C++`

Examples presented in this documentation

We describe here the examples used in the documentation. When installing ALIAS you will find a directory Examples providing other examples. Other examples of the use of interval analysis may be found on the HEPHAISTOS web page.

Example 2

This example comes from a planar robotics problem. Let the end-effector of the robot be a triangle. Each vertex of this triangle is connected to the ground via a linear actuator whose extremity is fixed point. We know the lengths of the three linear actuators (50, 26, 25) and we want to determine the pose of the end-effector i.e. the location of the vertex

and its orientation. We have therefore to solve a system of three equations in three unknowns.

The following Maple program enable to get the equations of this example.

 
with(linalg):
#location of the linear actuator on the ground
xa1:=0:ya1:=0:xa2:=10:ya2:=0:xa3:=3:ya3:=10:
#location of the linear actuator on the end-effector
xb1:=0;yb1:=0:xb2:=4:yb2:=0:xb3:=2:yb3:=2:
for i from 1 to 3 do
	OA.i:=array([xa.i,ya.i]):
	CBr.i:=array([xb.i,yb.i])
od:

rot:=array([[cos(teta),-sin(teta)],[sin(teta),cos(teta)]]):
for i from 1 to 3 do CB.i:=multiply(rot,CBr.i): od:
OC:=array([x,y]):
for i from 1 to 3 do
      AB.i:=evalm(OC-OA.i):
      AB.i:=evalm(AB.i+CB.i):
      ro.i:=dotprod(AB.i,AB.i,'orthogonal'):
      ro.i:=simplify(ro.i):
od:

eq1:=ro1-50:eq2:=ro2-26:eq3:=ro3-25:

The system admit the two solutions:

$\begin{displaymath} (5,5,0) (3.369707132, 6.216516219, -0.8067834380) \end{displaymath}$

Here we may use the general solving algorithm (section 2.3), the general solving algorithm with the gradient (section 2.4), the general solving algorithm with the gradient and Hessian (section 2.5).

These algorithms are implemented in the test program Test_Solve_General1, Test_Solve_Gradient_General1, Test_Solve_JH_General1

Example 3

In this example we will solve a trigonometric equation. This equation is derived from the previous example by subtracting the first equation to the second and third: this lead to a linear system in the unknowns x,y which are substituted in the first equation.

The following Maple program enable to get the equations of this example.

 
with(linalg):
xa1:=0:ya1:=0:xa2:=10:ya2:=0:xa3:=3:ya3:=10:
xb1:=0;yb1:=0:xb2:=4:yb2:=0:xb3:=2:yb3:=2:
for i from 1 to 3 do
      OA.i:=array([xa.i,ya.i]):
      CBr.i:=array([xb.i,yb.i])
od:

rot:=array([[cos(teta),-sin(teta)],[sin(teta),cos(teta)]]):
for i from 1 to 3 do CB.i:=multiply(rot,CBr.i): od:
OC:=array([x,y]):
for i from 1 to 3 do
      AB.i:=evalm(OC-OA.i):
      AB.i:=evalm(AB.i+CB.i):
      ro.i:=dotprod(AB.i,AB.i,'orthogonal'):
      ro.i:=simplify(ro.i):
od:

eq1:=ro1-50:eq2:=ro2-26:eq3:=ro3-25:

en1:=eq2-eq1:en2:=eq3-eq1:
sw:=solve({en1,en2},{x,y}):
assign(sw):
eq1:=numer(eq1):
eq1:=simplify(eq1,trig):
eq1:=convert(eq1,horner,[sin(teta),cos(teta)]):

This equation has 2 solutions 0, -0.8067834380 (or equivalently 5.47640187). Here we may use the general solving algorithm (section 2.3), the general solving algorithm with the gradient (section 2.4), the general solving algorithm with the gradient and Hessian (section 2.5) or the procedure devoted to trigonometric equation (section 2.13).

These algorithms are implemented in the test program Test_Solve_General2,
Test_Solve_Gradient_General2, Test_Solve_JH_General2, while for the the specific procedure devoted to solving trigonometric equations we may use the program Test_Solve_Trigo. In the later case we may use or not the procedure which compute bounds on the roots of the equation.

We may then investigate the computation time when we have a pretty good idea of the solution. For example we assume that we have a root in the range [5.3, 5.7]. We may now use Newton method (see section 2.9) implemented in the test program Test_Newton2, Brent's method (see section 2.8 and Ridder's method (see section 2.7) implemented in the test program Test_Ridder2.An interesting point is that although Newton is faster than the others methods we may encounter convergence problem in this example. For example if the initial guess is 5.85 (which is closer to the solution 5.476 than the second solution 0) Newton will converge toward the 0 solution.

Example 4

This example is similar to example 1 except that we deal with the spatial case. The pose of the end-effector is defined by 6 parameters: the coordinates x,y,z of a specific point on the end-effector and three angles p,t,h which define its orientation. We have now 6 linear actuators connecting the end-effector and the ground. The length of the linear actuator are all equal to 60. When expressing the leg lengths as function of the parameters we may extract from the 6 equations a linear system in x,y,z. Solving this system and substituting in the remaining equations leads to a system of three equations in the unknowns p,t,h. The following Maple program enable to compute these equations.

 
with(linalg):
xa1:= -9:ya1:=9:xa2:=9:ya2:=9:
xa3:=12:ya3:=-3:xa4:=3:ya4:=-13:
xa5:=-3:ya5:=-13:xa6:=-12:ya6:=-3:
xb1:= -3:yb1:=7:xb2:=3:yb2:=7:
xb3:=7:yb3:=-1:xb4:=4:yb4:=-6:
xb5:=-4:yb5:=-6:xb6:=-7:yb6:=-1:

rot:=array([[cos(p)*cos(h)-sin(p)*cos(t)*sin(h)
,-cos(p)*sin(h)-sin(p)*cos(t)*cos(h),
sin(p)*sin(t)],[sin(p)*cos(h)+cos(p)*cos(t)*sin(h),
-sin(p)*sin(h)+cos(p)*cos(t)*cos(h),-cos(p)*sin(t)],
[sin(t)*sin(h),sin(t)*cos(h),cos(t)]]):

for i from 1 to 6 do
      OA.i:=array([xa.i,ya.i,0]):
      CBr.i:=array([xb.i,yb.i,0]):
      CB.i:=multiply(rot,CBr.i):
od:

cen:=array([x,y,z]):

for i from 1 to 6 do
      AB.i:=evalm(cen-OA.i+CB.i):
      ro.i:=dotprod(AB.i,AB.i,`orthogonal`):
      ro.i:=simplify(ro.i,trig):
od:
for i from 1 to 6 do eq.i:=ro.i-60^2: od:
er1:=eq2-eq1:er2:=eq3-eq1:er3:=eq4-eq1:er4:=eq5-eq1:er5:=eq6-eq1:
sw:=solve({er1,er2,er3},{x,y,z}):
assign(sw):

en1:=numer(eq1):en2:=numer(er4):en3:=numer(er5):

for i from 1 to 3 do
      en.i:=simplify(en.i,trig):
      en.i:=convert(en.i,horner,[sin(p),cos(p),sin(t),cos(t),sin(h),cos(h)]):
od:

We are looking for a solution in the domain:

$\begin{displaymath}[4.537856054,4.886921908], [1.570796327,1.745329252], [0.6981317008, 0.8726646262] \end{displaymath}$

The system has a solution which is approximatively:

$\begin{displaymath} 4.6616603883, 1.70089818026, 0.86938888189 \end{displaymath}$

Here we may use the general solving algorithm (section 2.3), the general solving algorithm with the gradient (section 2.4), the general solving algorithm with the gradient and Hessian (section 2.5).

These algorithms are implemented in the test program Test_Solve_General, Test_Solve_Gradient_General, Test_Solve_JH_General (in that later case Kantorovitch theorem is applied only at level 1).

Examples of applications of interval analysis

ALIAS offers tools that may be used to solve many problems and interval analysis has a broad range of application. In this section we will present examples of realistic problems that have been solved by interval analysis. Some of them have been solved using directly the solving algorithms of ALIAS, for others it has been necessary to write additional C++ code. Other examples may be found in the HEPHAISTOS web page.

A geometrical example

The following example originated from the INRIA Geometrica project. It exemplifies that focusing on the problem at hand while keeping in view that interval analysis will be used allows one to develop a very efficient algorithm that is at the same time faster and safer (in term of quality of the result) than conventional approaches.

Consider 2 ellipses E1, E2 in the plane that are perfectly defined and the so-called bi-tangent i.e. the lines that are tangent to both ellipsis. There is 4 such lines but we assume that some criteria allows to choose two bi-tangents L1, L2. L1 intersects E1 at point P, E2 at and L2 intersects E1 at point R and E2 at point S. We construct now the vectors PQ, RS and then the determinant D= $\vert$ PQ RS $\vert$ . The problem is to determine the sign of D in a guaranteed manner (this sign is then used for another algorithm and a mistake in the sign has a very negative influence).

A classical approach to solve this problem is to consider that the 8 coordinates of the points P, Q, R, S are the unknowns, write 8 equations to determine these unknowns, solve the system and then determine the sign of D. But this approach has drawbacks:

the system of equations is complex
it is difficult to solve exactly

We may evidently use ALIAS to solve the system and uses the Newton procedure of ALIAS-Maple to compute the solution with a sufficient accuracy to state the sign of D. But this is overkill: we do not really want to determine the values of the coordinates of P, Q, R, S but only the sign of D.

Now we may note that the coordinates of the points are bounded as the points are included in the bounding box of the ellipses. Being given ranges for the unknowns we may compute the interval evaluation of the determinant. If the lower bound is positive or the upper bound is negative we may directly state the sign of the determinant. If not we bisect one the unknown coordinates: we has thus a list of boxes with 8 ranges in each box, one for each coordinate. For each box we check if the coordinates ranges allows the points P, Q, R, S to belong to the ellipsis and to the bi-tangents, otherwise we reject the box. Then we compute the interval evaluation of D: if the lower bound is positive we store the box in a special array of boxes, called the positive array and discard it from the list. Similarly if the upper bound is negative we store the box in the negative array and discard it from the list. When the list of boxes is exhausted we look at the number of elements in the positive and negative array: if one array has 0 element, then we have determined the sign of D. Otherwise we consider the array that has the lowest number of elements and restart the bisection procedure on this new list, eliminating boxes that do not describe points on the ellipsis or that are not on the bi-tangent. At the end of this process we may have eliminated all the boxes of the list or, in the worst case, we will have computed the coordinates of P, Q, R, S i.e. we will end up with the classical approach. Our test show however that this is seldom the case and the above procedure is much more faster than solving using the classical approach.

Still in some cases the sign of D cannot be safely computed: this may happen for example when some coordinates have very large values while other have very small one. Numerical round-off errors then prohibit the exact determination of the sign of D, a fact that is detected by interval analysis. But we may still in some cases solve the problem: for that purpose instead of using Cartesian coordinates we may use polar coordinates with different ranges for the unknowns in the determinant or we may use an extended arithmetics. In any case the algorithm is safe as it provides either a sign, which is guaranteed, or will state that the sign cannot be determined with the current arithmetics.

A robot kinematics example

We present here a simplified version of the problem (see [10] for a more detailed version).

Consider a plane in the 3D space, called the base, on which lie 6 points $A_1, A_2, \ldots, A_6$ whose coordinates in an arbitrary reference frame.

Consider another plane, called the platform, on which lie similarly 6 points $B_1, B_2, \ldots, B_6$ . To this plane we attach a frame, called the mobile frame. The coordinates of the 6 points in the mobile frame are supposed to be known. These 6 points constitute a rigid body which has a position/orientation with respect to the reference frame (i.e the location of any point of the rigid body may be calculated as soon as we know the coordinates of a point of this body in the reference frame and the rotation matrix that relates the mobile frame to the reference frame).

Assume now that the distances between each pair is fixed and is known. The problem is to determine what are the possible position/orientation of the rigid body such that these distance constraints are satisfied.

This problem is very important in practice. The platform is the "hand" of the robot and the distances between the may be changed by using actuators. The only information we have in the robot is obtained through sensors that measure the distances between the . Solving the above problem allows one to determine where is the hand of the robot by using the sensory information (but this problem has also other application such as robot calibration).

This problem is called the direct kinematics problem. It has a counterpart, the inverse kinematics problem: being given the position/orientation of the rigid body computes the distances between the pairs . This inverse kinematics problem has a straightforward solution: each squared distance can be calculated as a function of the parameters that describe the position/orientation of the rigid body. Hence solving the direct kinematic problem is equivalent to solve the system of equations of the inverse kinematics in the position/orientation parameters.

This problem is considered as one of the most difficult robot kinematics problem. Before 1992 the only known method to solve this problem was to use the Newton scheme and there was no theoretical result on this problem. Afterward with the use of sophisticated mathematics it has been possible to show theoretical results:

there will be at most 40 solutions, complex and real
examples with 40 real solutions have been exhibited
it is possible to reduce this problem to the the solving of a 40th order univariate polynomial

But still was lacking a practical algorithm to compute the solutions: indeed the manipulation needed to get the 40th order polynomial are difficult to automatize.

The fastest algorithm to solve this problem is the use of the Gröebner basis package of Faugère, Rouillier that allow to compute all the solutions in a computation time that ranges between a few seconds to less than 30 seconds.

Interval analysis allows to solve this problem. Basically we have noticed that we may choose as unknowns the coordinates of 3 points on the platform (called the reference points). Indeed the coordinates of the 3 other points may be obtained as linear combination of the 3 chosen points (i.e. they are virtual points). Furthermore the only equations we have are only distance equations: distances between the pairs and distances between the reference points and the virtual points. Hence the distance solving algorithm described in section 2.16 is convenient for this problem.

Trials have shown that the computation time ranges between 10 to 40 seconds, which is competitive with the algorithm of Faugère, Rouillier. Furthermore in most practical cases we are not interested in computing all the solutions but only the one that corresponds to the actual position/orientation of the platform and as the direct kinematics problem has to be solved almost continuously and the robot speed is limited we may determine a small search domain in which the current solution should be located. In that case the interval analysis based algorithm is very fast as it is sensitive to the search space (at the opposite of the Gröebner approach that has to compute all the solutions and then sort which one is the current solution and hence is working in a constant time). The algorithm is also safe compared to the Newton scheme that may converge toward a solution that is not the current one. Indeed we may guarantee that the current solution is included in the algorithm result. Furthermore if more than one solution is found then it is better to stop immediately the robot as the result of the calculation is used to control it.

A robot control problem

The problem presented here is for a robot described in the previous section. We have seen that the hand of the robot was moving with respect to its base by using linear actuators that allow to change the distance between the pairs of points . But in practice these actuators have a limited stroke and consequently the distance $\rho$ between the points has to lie within a given range:

$\begin{displaymath} \rho_{min} \le \rho \le \rho_{max} \end{displaymath}$

Furthermore the actuator is attached at point

by joints (typically ball-and-socket or universal joints) that have limited motion. Hence the platform may reach only a limited set of position/orientation that is called its workspace.

Assume now that the hand has to follow a time-dependent trajectory: it is clearly important to verify that all the points of this trajectory lie within the workspace of the robot. The trajectory is defined in the following manner: the position/orientation parameter are written as analytic function of the time T (which is assumed to lie in the range [0,1] without lack of generality). Using the solution of the inverse kinematics (see the previous section) it is then possible to express the distance $\rho$ as functions of the time. For the trajectory to lie in the workspace we have to verify the 12 inequalities:

$\begin{displaymath} \rho_{min} \le \rho(T) \le \rho_{max} \end{displaymath}$

when T lie in the range [0,1]. As the analytical form of the position/orientation parameters may be arbitrary we are looking for a generic algorithm that may deal with such arbitrary trajectory.

This can easily be done with interval analysis (see [9] for a detailed version). First we define the trajectory in Maple and compute the analytical form of $\rho(T)$ (and of any other constraint that may limit the workspace of the robot). We get a set of inequalities that has to be satisfied for any T in [0,1] if the trajectory lie within the workspace. The analytical form of these inequalities are written in a file: this allow their interval evaluation for any T range by using the ALIAS parser. Then the general solving procedure of ALIAS may be used to determine if there is a T such that at least one constraint is violated.

An important point is that the algorithm allow to deal with the uncertainties in the problem. A first uncertainty occurs when controlling the robot along its nominal trajectory. Indeed the robot controller is not perfect and there will be a positioning error: for a nominal value of the position/orientation parameters ${\bf X}$ the reached pose will be ${\bf X}+ \Delta{\bf X}$ where $\Delta{\bf X}$ can be bounded. A second uncertainty source is due to the differences between the theoretical geometrical model of the robot and its real geometry. Indeed to solve the inverse kinematics we use the coordinates of the in the reference frame and of the in the model frame. In practice however these coordinates are known only up to a given accuracy: hence these coordinates for the real robot may have any value within given ranges. Hence the inequalities of the problem have not fixed value coefficients but interval coefficients. But this no problem for interval analysis as the general solving procedures may deal with such inequalities. Hence if the algorithm find out that all inequalities are verified for any T in [0,1], then this means that whatever is the real robot and the positioning error of the robot controller the trajectory followed by the robot will fully lie within the robot workspace.

Robot singularity analysis

In the robot presented in the previous sections we have seen that the inverse kinematic relates the the distances $\rho$ between the to the position/orientation parameters of the platform X by $\rho = F({\bf X})$ . An important matrix is the jacobian matrix of this relation $J= ((\partial F/\partial X_i))$ . Indeed the forces $\tau$ in the legs are related to the forces/torques ${\cal F}$ applied on the platform by

$\begin{displaymath} {\cal F}=A J \tau \end{displaymath}$

where

is a matrix that is never singular. Hence for given forces/torques applied on the platform the force in each leg may be computed as a ratio whose denominator if $\vert AJ\vert$ . A configuration where $\vert J\vert=0$ is called a singularity of the robot. In this configuration the forces in the leg of the robot may go to infinity, causing a breakdown of the robot. Hence a very important practical problem is to be able to determine if there is a singularity within a given workspace ${\cal W}$ of the robot.

Usually this workspace is defined in the following manner: a geometrical object that will include all possible location of a specific point of the platform and ranges for the parameters that describe the orientation of the platform.

The determinant of can usually be expressed as a function of the position/orientation parameters. Interval analysis is appropriate to design an algorithm that check if there is a singularity within a given workspace. For that purpose we will take a point inside the workspace and calculate the value of $\vert J\vert$ at this point. Let us assume that this value is positive. A singularity will occur within the workspace if we are able to find another point in the workspace where $\vert J\vert$ will be negative.

We may assume that we are able to calculate a bounding box of the workspace and that we are able to design a test that allow to determine if a box for the position/orientation parameters is fully included in the workspace, is fully outside or part of it is inside and part of it is outside.

With that it is easy to design an algorithm that determine if the workspace includes a singularity (see [12] for more details).

First we use interval arithmetics to determine bounds for the value of $\vert J\vert$ . If the lower bound of the interval is positive is positive, then there is no singularity within the workspace. Otherwise we bisect the box. For the new boxes we first test if the box is inside the workspace: if one box is fully outside the workspace we discard it. If a box is not fully inside we bisect the box. For a box that is fully inside we compute the interval evaluation of $\vert J\vert$ . If the lower bound is positive we discard the box. If the upper bound is negative, then for any position/orientation defined by parameters within the box ranges the determinant will be negative: hence the workspace includes a singularity and we may stop the algorithm. If all the boxes in the list have been processed, then there is no singularity within the workspace.

Note that it is easy to generalize the algorithm so that uncertainties in the robot geometry are taken into account. A general version of this algorithm has been implemented using ALIAS and Maple and is able to deal with different robot architectures. Maple is used to compute the analytical form of $\vert J\vert$ . The ALIAS parser is used to perform the interval evaluation of the determinant.

Robot workspace analysis

For the robot presented in the previous examples we have a set of parameters ${\bf X}$ that allow to represent the position/orientation of the platform. At the same time we have various geometrical parameters that describe the possible geometry of the robot. Examples of the these parameters are the distance $\rho$ between the

, the angle $\theta_i$ between the vector ${\bf A_iB_i}$ and a fixed direction in space (this angle represent the amplitude of the motion of the joint we have at

In practice all the geometrical parameters are submitted to constraints. For example the distances $\rho$ must satisfy $\rho_{min} \le \rho \le \rho_{max}$ , the angle $\theta_i$ must be such that $\vert\cos\theta_i\vert=\vert{\bf A_iB_i}.{\bf n_i}/\rho_i\vert \ge \cos\theta_d$ where ${\bf n_i}$ is a unit vector that describes the main orientation of the ball-and-socket joint at and $\theta_d$ is the maximal possible rotation of this joint. All these constraints imply that the value of the elements of ${\bf X}$ are restricted to lie in a specific region embedded in the 6-dimensional space, this region being called the reachable workspace of the robot as the points of this region define all the position/orientation that can be reached by the platform.

In some cases it is possible to find an analytical description of the workspace (for example if the orientation is fixed and only the distance constraints are taken into account) but as soon as all the constraints are taken into account such analytical form is difficult to obtain. Interval analysis allows to obtain an approximation of the workspace as a set of 6-dimensional boxes. It is only an approximation as the algorithm, based on a classical bisection method, discard boxes whose width is lower than a given threshold. At the same time it is possible to obtain a bound on the error between the volume of the approximation and the volume of the workspace. For more details see [11]. A variant of the algorithm allows to solve efficiently a very practical problem: is a given region included in the reachable workspace of the robot ?

Robot synthesis example

The robot presented in the previous sections has numerous advantages but its performances are very sensitive to its geometry (i.e. to the location of the points ). The previous sections have presented analysis problems: analyze for a given robot what are its performance. But we may also consider an even more complex problem which is the synthesis problem i.e. find what should be the geometry of the robot such that it satisfies some performance criteria. This is very complex issue but one which has clearly a large impact in practice (for example when designing a robot whose load will be over 2 tons and whose accuracy should be better than a micrometer as considered by the European Synchrotron Radiation Facility in Grenoble).

Consider for example the following problem: what should be the geometry of the robot (i.e. the location of the and the limits $\rho_{min}, \rho_{max}$ on the $\rho$ ) such that a given set ${\cal W}$ of position/orientation $\{X_1,\ldots,X_n\}$ can be reached by the platform ?

The inverse kinematic analysis allows to obtain the constraints $\rho_{min} \le \rho \le \rho_{max}$ as a set of inequalities $F({\cal P},X_i) \le 0$ between the design parameters ${\cal P}$ and the elements of the set ${\cal W}$ . A classical approach to solve this problem will be to determine the set ${\cal P}$ that minimize the cost function $\sum_i F({\cal P}, X_i)$ . But this approach has many drawbacks:

we cannot guarantee to find even one solution
it will give at most a few solutions to the synthesis problem while in general there will be an infinite number of solutions
for a given solution the geometry of the real robot will be different from the theoretical solution due to the manufacturing tolerances. Hence we cannot guarantee that the real robot will really be able to reach the set ${\cal W}$

Interval analysis is a more appropriate approach. First of all it is reasonable to assume that the geometrical parameters are bounded as they define the overall size of the robot. We may thus define a box as a set of ranges, one for each design parameters. Using interval arithmetics we are then able to compute the lower and upper bounds of each

for each element of ${\cal W}$ . The different cases that may occur for a box are:

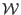
the lower bound of the interval for one 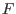is positive: we discard the box
the upper bound of the intervals for all 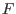is negative: the box is stored as a solution
the lower bound of the intervals for all 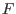is negative while their upper bound is positive: we bisect the box at the variable having the largest range except if all ranges have a width that is lower or equal to twice the manufacturing errors, in which case we discard the box

Using this approach we get not only one solution but ranges for the solution: indeed each point of the solution boxes satisfy all inequalities which means that the theoretical robot will be able to reach all the elements of ${\cal W}$ . But we may take also the manufacturing errors $\epsilon$ into account. Indeed for a range A= $[\underline{x},\overline{x}]$ in a solution box we may consider the range AP= $[\underline{x}+\epsilon,\overline{x}-\epsilon]$ that is included in the previous range and exists as the ranges of a solution box have a width at least $2\epsilon$ . If we choose as design parameter a point in AP, then for the real robot the design parameter value will be included in A. As this is true for all the design parameters, then we may guarantee that the real robot will be able to reach all elements of ${\cal W}$ .

Using this approach we are able to find all the geometries such that the real robot satisfy the workspace constraints. Now we may consider another design criteria and use the same approach, that will lead to another set of design parameters. Taking the intersection of this set with the set obtained for the workspace we will be able to compute all robot geometries that satisfy the new design criteria and the workspace constraint.

Here again interval analysis is an elegant approach that allows to solve a very practical problem. This approach has been used by the HEPHAISTOS project in various industrial contracts.

A quantum mechanics example

The Kochen-Specker theorem is one of the more important in quantum mechanics. Its a application involves the solving of the following problem (that has been simplified for the sake of clarity).

Consider unit vectors named 1,2,..9,A,B,..Z in a four dimensional space. A group of vectors is a set of 4 vectors that have to be orthogonal to each other and not identical or opposite. A m-sequence is a set of m groups such that:

each vector in the sequence has the color black or white
in each group of the sequence there must be exactly 3 black vectors and one white vector

The smallest known sequence is a 9-sequence named the Cabello's system:

 
1234,4567,789A,ABCD,DEFG,GHI1,35CE,29BI,68FH

which involves 18 vectors.

Our objective is to to make an exhaustive search of m-sequences. For that purpose we use a software designed by B.D. McKay, called the generator, that provides for any set of a vectors and any sequence with b groups all the b-sequences that satisfy the color constraints and are not isomorphic (for example changing the name of the vectors will lead to the same sequence). Then we consider each potential b-sequence and we must check if there are at least one set of coordinates for the vectors such that the orthogonality constraints for each group are satisfied together with the non-collinearity between the vectors.

Such verification is not so easy. Indeed the orthogonality constraints for a group involves 6 equations: consequently for a b-sequence with a vectors we have 6b orthogonality equations, a equations that indicate that the vectors are unitary. If we consider for example the Cabello's system the number of equations is therefore already 74 for 72 unknowns. Although the problem is algebraic the solving method in algebraic geometry have difficulties to handle such number of equations (for a sequence that is one of the smallest).

A second problem is that an exhaustive enumeration of all potential b-sequences leads to a very large number of sequences. For example for a=10 and b=12 the number of sequences is 197 885 058 $\ldots$

Nevertheless the problem was convenient for interval analysis. Indeed the unknown coordinates are component of unitary vectors and hence will lie in the range [-1,1]. Furthermore if a vector is solution then its opposite is also solution: hence we may restrict one of the coordinates of the vector to lie in the range [0,1]. In the same manner any rotation applied simultaneously to all solution vectors will lead to another set of solution vectors. Hence we may choose arbitrary any group so that its vectors constitutes an orthogonal basis of the four dimensional space. The coordinates of the vectors in this group will then be (1,0,0,0), (0,1,0,0), (0,0,1,0) and (0,0,0,1). Furthermore if one of these vectors appears in another group, then the orthogonality constraint will imply that one coordinate of all vectors of this group (except the basis vector) will be 0.

To solve this problem we have then developed a first very fast interval analysis algorithm that has been incorporated in the generator and eliminates sequence that trivially will have no solution. For example a sequence starting with 1234,1235 will be eliminated as 5 should be 4 or -4. This algorithm drastically reduces the number of generated sequences. Then for the remaining sequences we have used a general solving procedure of ALIAS. Even with the above simplification the size of the systems are large: for Cabello's system we have reduced the problem to 32 unknowns and 82 equations that can be solve in about 60 seconds on a laptop. But eliminating sequence without solution is usually faster. For example the system

 
1234,1256,1378,129A,24BC,34DE,5DFG,7HIJ,8BFK,9ADE,CGHI,6EJK

with 59 equations and 26 unknowns is eliminated in 10 seconds.

Although this work has not been completed yet we have already shown that Cabello's system is the smallest sequence (all sequences with a smaller number of groups have no solution).