Currents for shape representation
Currents are used to represent the shapes  i and the residuals ϵi of the forward model.
Before going into the mathematical details, let consider a simple example. In the recent years,
3D scanners have been developed to digitalise 3D objects. These machines acquire the
geometry of an object by probing its surface with laser beams. The diffraction of the beams
on the surface is captured by cameras and the resulting signal is used to reconstruct the virtual
object. Likewise, currents characterise shapes by probing them using varying vector fields
ω ∈ W , like virtual laser beams. The shape is characterised by how it integrates these vector
fields (Figure 1).
i and the residuals ϵi of the forward model.
Before going into the mathematical details, let consider a simple example. In the recent years,
3D scanners have been developed to digitalise 3D objects. These machines acquire the
geometry of an object by probing its surface with laser beams. The diffraction of the beams
on the surface is captured by cameras and the resulting signal is used to reconstruct the virtual
object. Likewise, currents characterise shapes by probing them using varying vector fields
ω ∈ W , like virtual laser beams. The shape is characterised by how it integrates these vector
fields (Figure 1).
 |  |
Mathematically, a current is a continuous linear mapping 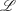 W (ω) from a vector space W
to ℝ, i.e. it is an application that integrates vector fields. The current of a surface
W (ω) from a vector space W
to ℝ, i.e. it is an application that integrates vector fields. The current of a surface 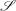 is the flux
of a test vector field ω ∈ W across that surface. The shape
is the flux
of a test vector field ω ∈ W across that surface. The shape  of the surface S is uniquely
characterised by the variations of the flux as the test vector field varies. The core element that
makes this framework possible is to choose the vector space of the test vector fields W as the
vector space generated by a Gaussian kernel KW (
of the surface S is uniquely
characterised by the variations of the flux as the test vector field varies. The core element that
makes this framework possible is to choose the vector space of the test vector fields W as the
vector space generated by a Gaussian kernel KW ( ,
, ) = exp(-∥
) = exp(-∥ -
- ∥2∕λW 2) (W is a
reproducible kernel Hilbert space (r.k.h.s.)). W is the dense span of basis vector fields of the
form ω(
∥2∕λW 2) (W is a
reproducible kernel Hilbert space (r.k.h.s.)). W is the dense span of basis vector fields of the
form ω(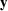 ) = KW (
) = KW (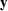 ,
, )
) , where the vectors
, where the vectors  are given and fixed at the spatial positions
are given and fixed at the spatial positions
 . The kernel KW defines an inner product in W that can be easily computed by
< ω(.),ν(.) > W =< KW (.,
. The kernel KW defines an inner product in W that can be easily computed by
< ω(.),ν(.) > W =< KW (., )
) ,KW (.,
,KW (.,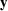 )
)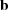 > W =
> W =  T KW (
T KW ( ,
,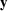 )
)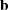 , where ω(.) = KW (.,
, where ω(.) = KW (., )
) and
ν(.) = KW (.,
and
ν(.) = KW (.,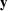 )
)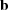 are two vector fields of W . A consequence of these properties is that
the space of currents W*, which is the dual of W , is the dense span of the dual
representations of the basis vectors ω(.), called Dirac delta currents δ
are two vector fields of W . A consequence of these properties is that
the space of currents W*, which is the dual of W , is the dense span of the dual
representations of the basis vectors ω(.), called Dirac delta currents δ
 (ω) and defined
by:
(ω) and defined
by:
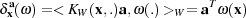 | (1) |
Intuitively, a Dirac delta current is an infinitesimal vector  that is concentrated at the
spatial position
that is concentrated at the
spatial position  . In that way, the current of a surface S can be decomposed into an
infinite set of Dirac delta currents defined at each point of the surface and orientated
along the surface normal. In our application, the surfaces are represented by discrete
triangulated meshes. Their current representation is therefore given by the finite
sum:
. In that way, the current of a surface S can be decomposed into an
infinite set of Dirac delta currents defined at each point of the surface and orientated
along the surface normal. In our application, the surfaces are represented by discrete
triangulated meshes. Their current representation is therefore given by the finite
sum:
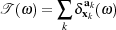 | (2) |
where  k are the barycentres of the mesh faces and
k are the barycentres of the mesh faces and  k their normal (Figure 2). The vector
field ω dual of the current
k their normal (Figure 2). The vector
field ω dual of the current  (ω) is the spatial convolution of every normal vector
(ω) is the spatial convolution of every normal vector  k with the
kernel KW , ω(
k with the
kernel KW , ω( ) = ∑kKW (
) = ∑kKW ( ,
, k)
k) k. In [1], the authors propose an efficient greedy algorithm
to approximate the current representation of a surface by a minimal yet optimal set of
Dirac delta currents (Figure 2). Computational complexity is further decreased
by using FFT-based convolution techniques to compute the kernel convolutions.
k. In [1], the authors propose an efficient greedy algorithm
to approximate the current representation of a surface by a minimal yet optimal set of
Dirac delta currents (Figure 2). Computational complexity is further decreased
by using FFT-based convolution techniques to compute the kernel convolutions.
| Original Shape (1476 delta currents) | Compressed Shape (281 delta currents) |
 |  |
As currents are linear applications, they define a vector space on shapes. The
sum of two currents is the union of their Dirac delta currents, i.e. the union of the
two surfaces. Likewise, scaling a current amounts to scaling the amplitude of the
Dirac delta currents. By construction, the space of currents W* is equipped with the
inner-product < δ
 (ω),δ
(ω),δ
 (ω) > W* =< KW (
(ω) > W* =< KW ( ,.)
,.) ,KW (
,KW (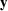 ,.)
,.)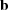 > W =
> W =  T KW (
T KW ( ,
,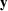 )
)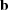 .
The distance between two shapes can therefore be computed as the norm of the
difference of their currents. The space of currents thus enables us to compute mean,
standard deviations and other descriptive statistics on shapes. Similarly, Gaussian
variables in the space of currents can be defined. In practice, we place at each point
.
The distance between two shapes can therefore be computed as the norm of the
difference of their currents. The space of currents thus enables us to compute mean,
standard deviations and other descriptive statistics on shapes. Similarly, Gaussian
variables in the space of currents can be defined. In practice, we place at each point  p
of a 3D grid embedding the shape
p
of a 3D grid embedding the shape  a random vector
a random vector  p that follows a normal
distribution.
p that follows a normal
distribution.
The width λW of the kernel KW controls the resolution of the current representation. The larger λW , the coarser the resolution and the less “accurate” the representation. This parameter thus controls the level of shape details we want to study. As it is illustrated in Figure 3, small λW values enable capturing little differences between surfaces, whereas large λW discard them.
A)  | B)  |
References
[1] S. Durrleman, X. Pennec, A. Trouvé, and N. Ayache, “Statistical models on sets of curves and surfaces based on currents,” Medical Image Analysis, vol. 13, pp. 793–808, Oct. 2009.