ExoShape : shape statistics with currents

Let a population of N patients whose heart has been segmented from medical images. The cardiac anatomy of a patient is represented by a triangulated surface mesh defining the boundaries of the organ (Figure 1). We assume that the meshes have been rigidly aligned to a common space [3, 4, 5]. The first step of the analysis consists in computing an unbiased atlas of the population and in estimating the transformations that map this atlas to the observations. We call shapes, or observations, the computational representation of the continuous surfaces Sⁱ and denote them by ⁱ, the superscript i standing for the patient index. It is important to differentiate the continuous surface Sⁱ, which represents the cardiac anatomy, and its computational representation ⁱ. In the large majority of applications, ⁱ is a triangulated mesh that approximates Sⁱ. In this framework, the ⁱ’s are currents.

To create the average template of the cardiac anatomy observed in the population, we make use of the forward strategy proposed by [1]. In the forward approach, the shapes ⁱ are modelled as the sum of an ideal template deformed by a diffeomorphic transformation ϕⁱ and some residuals ϵⁱ that encode the shape features that cannot be captured by the template. Mathematically, the forward model writes:

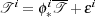(1)

In this equation, * denotes the action of the transformation ϕⁱ upon the template . Ideally, does not depend on the individuals that have been used to estimate it. In this case, the shape information of an observation is uniquely and universally encoded by both the transformation ϕⁱ and the residuals ϵⁱ. As the transformation ϕⁱ is smooth and diffeomorphic, it captures the shape information that is present in the template up to the transformation smoothness. Topology changes for instance cannot be captured as they break the diffeomorphic assumption. Similarly, shape patterns with high spatial frequency are discarded by the smoothness of the transformation. All these “residual” features are encoded by the residuals ϵⁱ.

Three elements are required to apply the forward model: a consistent way to represent shapes and residuals, a model of transformations that matches two shapes and an algorithm to estimate a template that is not biased by the population that is used to create it. In the framework used in this work, the shape and residuals are represented by currents, an elegant mathematical tool that defines a vector space on shapes, thus enabling statistical analyses on shapes [2]. The transformations are modelled with the Large Deformation Diffeomorphic Metric Mappings (LDDMM) [7]. Finally, the template and the transformations ϕⁱ are estimated simultaneously with an alternate minimisation. The main concepts of the methodology are outlined in the following paragraphs. The reader is referred to [2, 8] for further details.

• Currents for shape representation

• Surface registration with LDDMM & currents

• Atlas construction

References

[1]    S. Durrleman, X. Pennec, A. Trouvé, and N. Ayache, “A forward model to build unbiased atlases from curves and surfaces,” in Proc. of the International Workshop on the Mathematical Foundations of Computational Anatomy (MFCA-2008) (X. Pennec and S. Joshi, eds.), September 2008.

[2]    S. Durrleman, X. Pennec, A. Trouvé, and N. Ayache, “Statistical models on sets of curves and surfaces based on currents,” Medical Image Analysis, vol. 13, pp. 793–808, Oct. 2009.

[3]    F. Bookstein, “Size and shape spaces for landmark data in two dimensions,” Statistical Science, vol. 1, no. 2, pp. 181–222, 1986.

[4]    I. Dryden and K. Mardia, Statistical shape analysis. Wiley New York, 1998.

[5]    B. Jian and B. Vemuri, “A robust algorithm for point set registration using mixture of Gaussians,” in Proc. ICCV 2005, vol. 2, pp. 1246–1251, 2005.

[6]    Y. Zheng, A. Barbu, B. Georgescu, M. Scheuering, and D. Comaniciu, “Four-chamber heart modeling and automatic segmentation for 3-d cardiac ct volumes using marginal space learning and steerable features,” IEEE transactions on medical imaging, vol. 27, no. 11, pp. 1668–1681, 2008.

[7]    M. Vaillant and J. Glaunes, “Surface matching via currents,” in Proc. IPMI 2005, p. 381, Springer, 2005.

[8]    S. Durrleman, Statistical models of currents for measuring the variability of anatomical curves, surfaces and their evolution. PhD thesis, Université Nice-Sophia Antipolis, March 2010.