Atlas construction

The template and the deformations ϕⁱ are estimated jointly and consistently by means of an alternate two-step strategy. The idea is to consider the forward model as a Bayesian problem where the shapes ⁱ are the observations, the template is the unknown, the transformations ϕⁱ that register to the observations are hidden variables and the residuals ϵⁱ are random Gaussian represented by currents. To find and the ϕⁱ simultaneously, the problem is approximated by the minimisation problem:

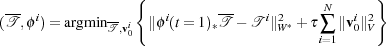(1)

where τ is weights the geodesic regularisation and ₀ⁱ is the initial velocity field that parameterises the transformation ϕ. This minimisation problem is very similar to the registration energy. The first term is the distance between two currents, the transformed template ϕ_*ⁱ and the target subject ⁱ. The second term is the geodesic regularisation, applied to all the transformations to estimate.

[1] proposed an alternate minimisation of that energy. Assume the template known, minimising (1) with respect to the ϕⁱ’s amount to registering the present estimate of the template to each patient independently. Once the ϕⁱ’s are found, (1) is minimised with respect to the template . This is achieved using a gradient descent method, see [1] for details. Intuitively, this step updates the template from the transformations ϕⁱ to reduce the overall registration error. The new template minimises the registration errors for all the patient at the same time, i.e. it is more centred with respect to the population. The algorithm is initialised with the mean current of all the observations and it is iterated until convergence (Figure 1). In all our experiments, we fixed τ = 10^-3 and adjusted the more intuitive kernel sizes λ_V ² and λ_W ².

A- Estimate the Transformations ϕi	B- Centre the Template

Figure 1: Joint estimation of template and transformations Given a template, the transformations that map it to the shapes are first estimated (A). The template is then centred to minimise the overall registration error (B).

A parallel implementation of the algorithm has been developed to process large amounts of subjects on clusters of computers. A scheduler script controls the execution of the algorithm. It dispatches the template-to-patient registrations to all the available computers as these steps are independent from each other (Figure 1, Step A). It then waits for the computers to perform the registrations, after what it centres the template (Figure 1, Step B) and loop until convergence. As a result, the computation time required to estimate the template minimally depends on the number of subjects.

References

[1]    S. Durrleman, X. Pennec, A. Trouvé, and N. Ayache, “Statistical models on sets of curves and surfaces based on currents,” Medical Image Analysis, vol. 13, pp. 793–808, Oct. 2009.