Dans la mesure où les seules données auxquelles on accède sont
sur la frontière extérieure du domaine, les différents types
d'approximants que nous allons considérer seront des approximants
des valeurs au bord. Afin d'utiliser des méthodes d'approximation
connues, il sera nécessaire de nous ramener au cas où le domaine
D est le disque unité
![]() .
.
On pourra alors considérer les meilleurs approximants rationnels ou
méromorphes de F sur le cercle unité
![]() pour les
normes L2 et
pour les
normes L2 et ![]() .
.
On notera toutefois que ceci n'induit pas nécessairement une perte
de généralité. Il est en effet connu [26, ch. 10] que
l'application conforme qui envoie
![]() sur D conserve leurs espaces
H2N et
sur D conserve leurs espaces
H2N et
![]() respectifs.
respectifs.
Les types d'approximants que nous allons considérer sont, d'une part le
meilleur approximant dans RN au sens de la norme L2, et d'autre
part le meilleur approximant dans
![]() au sens de la norme
au sens de la norme
![]() ,
obtenu par un résultat d'Adamjan, Arov et Krein
(AAK) que nous présentons plus loin.
,
obtenu par un résultat d'Adamjan, Arov et Krein
(AAK) que nous présentons plus loin.
En fait, dans les deux cas, p=2 et ![]() ,
il s'agit d'approximer
une fonction
,
il s'agit d'approximer
une fonction ![]() par une fontion
par une fontion
![]() .
Mais dans
le cas où p=2, on obtient, grâce à l'orthogonalité
.
Mais dans
le cas où p=2, on obtient, grâce à l'orthogonalité
![]() et grâce à l'inclusion
et grâce à l'inclusion
![]() ,
que
gN = PH2(f)+rN où
,
que
gN = PH2(f)+rN où
![]() est le meilleur approximant de
est le meilleur approximant de
![]() .
C'est sous cette dernière formulation que nous aborderons
l'approximation pour la norme L2.
.
C'est sous cette dernière formulation que nous aborderons
l'approximation pour la norme L2.
On s'intéresse ici au meilleur approximant rationnel pour la norme L2. Le problème se formule de la manière suivante :
Pour une fonction
![]() , trouver un couple de polynômes
(p,q) de degrés respectifs n-1 et n, tels que q ait ses zéros dans
, trouver un couple de polynômes
(p,q) de degrés respectifs n-1 et n, tels que q ait ses zéros dans
![]() et tels que
et tels que
| (2.17) |
La méthode que nous utilisons pour déterminer ce meilleur approximant
s'appuie sur un algorithme itératif de type quasi-Newton, implémenté
dans le logiciel d'approximation rationnelle Hyperion développé
au sein du projet MIAOU.
Nous présentons ici quelques résultats sur lesquels s'appuie cette
méthode.
Cette approche étant numérique, et dans la mesure où l'on ne
connaît f que sur un échantillon de valeurs sur
 ,
on ne
cherchera à estimer en fait qu'un nombre fini de ses coefficients de
Fourier. Il sera donc naturel, de considérer ici f comme un polynôme
trigonométrique de degré m.
,
on ne
cherchera à estimer en fait qu'un nombre fini de ses coefficients de
Fourier. Il sera donc naturel, de considérer ici f comme un polynôme
trigonométrique de degré m.
Définissons alors le polynôme g comme ceci :
| (2.18) |
 )
et définissons A et B par une division
euclidienne, de telle sorte que
)
et définissons A et B par une division
euclidienne, de telle sorte que
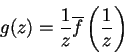 |
(2.19) |
| (2.20) |
 par rapport aux coefficients du polynôme q.
La démonstration de ce théorème est immédiate car on vérifie sans
peine que
par rapport aux coefficients du polynôme q.
La démonstration de ce théorème est immédiate car on vérifie sans
peine que
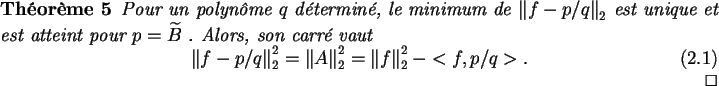 est orthogonal à zk/q pour
est orthogonal à zk/q pour
 .
Pour plus de détails sur les équations aux points critiques et la
convergence de l'algorithme, on renvoie le lecteur à [31,13,17].
.
Pour plus de détails sur les équations aux points critiques et la
convergence de l'algorithme, on renvoie le lecteur à [31,13,17].
Avant de mettre en uvre cet algorithme qui est un algorithme de descente
conjugué avec une méthode de Newton, il est bien sûr naturel de
s'interroger sur l'existence et l'unicité de tels approximants rationnels.
Si l'existence d'un meilleur approximant est toujours assurée
(on pourra par exemple se référer à [11,12] pour une
preuve de cette propriété dans un cas plus général), l'unicité
en revanche n'a pas lieu en général.
Parmi les résultats obtenus, on citera notamment les travaux menés
par L. Baratchart, E. B. Saff et F. Wielonsky [17], puis de
L. Baratchart, H. Stahl et F. Wielonsky à paraître [19],
d'où il ressort que le critère
![]() n'admet
qu'un seul point critique à l'ordre n (donc un minimum) par
rapport aux coefficients de q si, pour chaque point critique p/q,
il existe des polynômes A et B de degrés respectifs n-2 et
n-1 tels que A/B interpole f en 2n-2 points de
n'admet
qu'un seul point critique à l'ordre n (donc un minimum) par
rapport aux coefficients de q si, pour chaque point critique p/q,
il existe des polynômes A et B de degrés respectifs n-2 et
n-1 tels que A/B interpole f en 2n-2 points de
![]() et tels que
et tels que
| (2.21) |
Les auteurs de [19] utilisent ce critère pour prouver l'unicité
asymptotique ( i.e pour un ordre assez grand dépendant de f)
dans le cas où la fonction f approximée est une fonction de Markov
dont la mesure est à support dans (-1,1) et satisfait la condition
de Szegö ;
rappelons ici qu'une fonction est dite de Markov si elle est la transformée
de Cauchy d'une mesure positive à support compact sur l'axe réel, en
d'autres termes si elle s'écrit
| (2.22) |
 ,
mais seulement la valeur en des points critiques, est
donné dans un article à paraître de L. Baratchart et
F. Seyfert [18] mais ne concerne pour l'instant que la réduction
d'un ordre n à l'ordre n-1.
En tout état de cause, la présence possible de minima locaux oblige
l'algorithme d'approximation à effectuer un certain nombre d'intégrations
à partir de points initiaux pour pouvoir se convaincre que l'on a trouvé
un minimum global, c'est-à-dire un meilleur approximant.
,
mais seulement la valeur en des points critiques, est
donné dans un article à paraître de L. Baratchart et
F. Seyfert [18] mais ne concerne pour l'instant que la réduction
d'un ordre n à l'ordre n-1.
En tout état de cause, la présence possible de minima locaux oblige
l'algorithme d'approximation à effectuer un certain nombre d'intégrations
à partir de points initiaux pour pouvoir se convaincre que l'on a trouvé
un minimum global, c'est-à-dire un meilleur approximant.
Bien que l'algorithme donné dans l'article de L. Baratchart, M. Cardelli et M. Olivi [13] (généralisé au cas matriciel par P. Fulchieri et M. Olivi [29]) et implémenté dans [31] par J. Grimm, ait une stratégie plutôt efficace pour engendrer des minima locaux à partir de ceux des ordres précédents, ceci pose parfois des problèmes pour le temps de calcul de tels approximants.
Remarquons malgré tout que les résultats de convergence des pôles sur lesquels se fonde la présente approche sont valables pour toute suite de minima locaux et pas seulement les minima absolus.
Nous allons ici rappeler quelques résultats connus relatifs à
l'approximation analytique ou méromorphe pour la norme ![]() .
Ceux-ci ont été initialement développés pour résoudre le
problème de Nehari :
.
Ceux-ci ont été initialement développés pour résoudre le
problème de Nehari :
Pour f une fonction ![]() , trouver g dans
, trouver g dans ![]() qui réalise la condition
qui réalise la condition
Un outil essentiel pour résoudre ce problème (et les problèmes
connexes comme l'approximation méromorphe) est l'opérateur
de Hankel :
Pour f une fonction ![]() ,
on appelle opérateur de Hankel
de symbole f l'opérateur défini par
,
on appelle opérateur de Hankel
de symbole f l'opérateur défini par
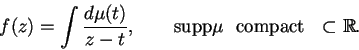 |
(2.24) |

![]()
En fait, la condition pour que Hf admette un vecteur maximisant
est remplie, dès lors que Hf est compact. Par le théorème de
Hartman [39, thm. 3.20], on sait que Hf est compacte si et
seulement si f est
 .
.
Ces deux résultats ont été significativement généralisés
par Adamjan, Arov et Krein [2] qui ont résolu par cette
généralisation la question d'exprimer le meilleur approximant
dans
![]() pour la norme
pour la norme ![]() :
:
Dans tout ce qui suit, on supposera que les vecteurs vN sont normalisés
de telle sorte que
![]() .
Ce second type d'approximant, de par son expression explicite, s'avère
beaucoup plus rapide à calculer que l'approximant L2. Les deux modes
sont néanmoins complémentaires dans la mesure où la norme L2 est
moins sensible aux ``petites'' perturbations comme le bruit de mesure, et
présente de ce fait un caractère plus robuste dans un cadre
numérique.
.
Ce second type d'approximant, de par son expression explicite, s'avère
beaucoup plus rapide à calculer que l'approximant L2. Les deux modes
sont néanmoins complémentaires dans la mesure où la norme L2 est
moins sensible aux ``petites'' perturbations comme le bruit de mesure, et
présente de ce fait un caractère plus robuste dans un cadre
numérique.
Le choix de ces deux modes d'approximation parmi d'autres à notre
disposition comme les approximants de Padé ou simplement la troncature
des séries de Fourier, n'est bien sûr pas innocent.
Dans le chapitre suivant, nous montrons en quoi ces deux modes d'approximation
présentent des caractéristiques communes, et plus particulièrement
comment on peut obtenir de ces deux formes une relation
``d'orthogonalité non hermitienne'' dont nous tirerons des informations
sur la position relative des pôles et de la fissure ![]() .
.
Mentionnons aussi l'impossibilité numérique d'utiliser les approximants de Padé où la troncature de la série de Fourier, leur comportement étant instable avec les erreurs numériques sur le développement. En fait, on pourrait montrer qu'aucun schéma linéaire n'est robuste dans la situation présente.