9 Améliorer le fonctionnement du CDPR, partie 2

Dans cette seconde partie nous allons présenter des approches encore expérimentales qui permettent d'aller encore plus loin dans l'amélioration des performances d'un CDPR. Ces approches ont été mises en oeuvre dans notre dernier prototype de CDPR, MARIONET-3D.

Pour un CDPR à 4 câbles le système décrit dans la section précédente ne résoudra pas toujours le problème de savoir quels sont les câbles non tendus, information nécessaire pour connaître la position du CDPR, mais permettra dans une certaine mesure de ne pas avoir un câble très détendu. Pour une détection plus sure des câbles non tendus nous allons nous intéresser à leur forme.

9.1 La forme d'un câble non tendu

Dispose t'on une autre caractéristique qui permettrait d'identifier qu'un câble n'est pas tendu ? Pour répondre à cette question il faut examiner la forme d'un câble attaché en 2 points fixes (ici les points $A$ et $B$) et de longueur supérieur à la distance entre $A$ et $B$. C'est un sujet qui a été très étudié en génie civil et on va se limiter au cas où le matériel du câble n'est pas élastique. On a alors affaire à un câble dit caténaire dont la forme est parfaitement connue à partir du moment où l'on connaît la position des points fixes et la longueur du câble. Un exemple de caténaire est présenté dans la figure 18.

Figure 18: La forme d'un câble non tendu

On voit qu'il y a une différence sensible entre la forme caténaire et le câble tendu et qu'en particulier l'angle entre le câble et l'horizontal varie tout au long du câble. Pour donner une idée un câble synthétique d'environ 5 mètres aura en $B$ une différence d'angle entre le câble tendu et le détendu d'environ 2.5 degrés (ce qui est visuellement détectable) si la longueur du câble est de 2 cm plus long que la longueur tendue. La vidéo suivante montre la déformation d'un câble Dyneema de 3mm de diamètre, fixé à deux points fixes et dont on augmente progressivement la longueur. La longueur initiale est de 600cm.

VIDEO

De quoi avons nous besoin pour avoir la forme du câble dans sa position actuelle ? On peut montrer que l'intégralité du câble se trouve en général dans le plan vertical qui contient les deux points d'attache et que pour obtenir sa forme il faut avoir 3 informations sur le système, par exemple la position de $B$ (2 paramètres) et la longueur du câble. Malheureusement à ce stade nous n'avons pas ces informations de manière précise.

: Si un câble non élastique de longueur $L$ dans une matière de densité linéaire $\mu$, attaché à un point fixe à une extrémité, est soumis à son extrémité libre à une force de composante horizontale $F_x$ et verticale $F_z$. On suppose que le point fixe du câble est l'origine du repère avec l'axe $x$ horizontal et l'axe z vertical vers le haut. Alors les coordonnées $x_b, z_b$ de son extrémité libre sont données par:

$$x_b = {\frac {{F_x}^{2}}{\mu\,g} \left( {\rm arcsinh} \left({\frac {F_z... ...}\right)-{\rm arcsinh} \left({\frac {-L\,g\mu+F_z}{{F_x}^{2}}}\right) \right) }$$ (10)

$$z_b = {\frac {1}{\mu\,g} \left( \sqrt {{F_x}^{4}+{F_z}^{2}}- \sqrt {{F_x}^{4}+ \left( -L\,g\mu+F_z \right) ^{2}} \right) }$$ (11)

On voit ici que la simple donnée de $x_b, z_b$ ne suffit pas à calculer la longueur du câble puisque nous avons 2 équations pour 3 inconnues ($L, F_x, F_z$). On ne peut donc pas résoudre le modèle géométrique inverse câble par câble. Mais examinons le cas d'un CDPR à 3 câbles. Comme pour chaque câble nous avons 3 inconnues nous avons donc un total de 9 inconnues. En terme d'équations nous avons 6 équations issues des 2 contraintes ci-dessus plus les trois équations d'équilibre du système (2), donc au total 9 équations. D'une manière générale ce type de système a un nombre fini de solution mais malheureusement il n'existe pas de formule qui permet de les calculer. Il faut alors utiliser une procédure numérique. Toutefois en première approximation supposer les câbles idéaux sera suffisant pour des petits ou moyens CDPR.

Si $x_b, z_b$ et $L$ sont connus on peut calculer numériquement $F_x, F_z$ mais là aussi il n'y a pas de formule donnant directement leurs valeurs. En introduction à la section suivante on va s'intéresser à la pente du câble à l'abscisse curviligne $s$ (compris entre 0 et $L$) est alors

$$\frac{F_z+\mu g(s-L)}{F_x}$$

Cette équation illustre le fait que si l'on est capable de mesurer la pente pour un $s$ donné on obtient alors une relation simple entre $F_x$ et $F_z$ qui permet, par exemple, d'exprimer $F_z$ en fonction de $F_x$. Si de plus on connaît $x_b, z_b$ les équations ci-dessus n'ont plus que deux inconnues ($L, F_x$) et l'on peut donc résoudre numériquement ce système pour calculer $L$.

Il existe une version plus élaborée des équations (10), (11) qui permet de prendre en compte l'élasticité du matériel du câble via la donnée de son module de Young. Cette formule n'a cependant qu'un intérêt pour les câbles très élastique et/ou de grande dimensions. Dans ce cas les modèles géométriques aussi bien inverse que directe peuvent avoir plusieurs solutions (on a trouvé des exemples avec 5 solutions au modèle géométrique inverse et plus d'une trentaine au modèle direct). Toutefois la résolution complètes (c'est-à-dire trouver l'ensemble des solutions) de ces modèles restent encore un problème ouvert car les algorithmes capables de calculer les solutions sont coûteux en temps de calcul. Toutefois dans le cas de l'exploitation d'un CDPR il existe des méthodes numériques très rapides qui peuvent résoudre le modèle direct en exploitant le fait qu'entre deux calculs de ce type la variation de longueur des câbles est très faible et donc la solution correspondante à l'état du CDPR doit être très proche de la solution précédemment trouvée.

9.2 Mesurer les angles d'un câble

9.2.1 Les deux angles d'un câble et leur mesure

Pour le moment nous avons parlé de l'angle $ax$ du câble avec l'horizontal mais on peut aussi considérer celui autour de l'axe vertical $az$. Pour une position de $B$ connue cet angle $az$ est unique pour chaque câble. Pour les CDPR à 4 câbles nous avons vu que selon la configuration qui est utilisé pour calculer la position de $B$ à partir des longueurs des câbles nous obtenons des positions différentes et donc des angles $az$ distincts. Toutefois les positions de $B$ restent relativement voisines et en conséquence les différences entre les angles $az$ vont être faibles. Si l'on veut utiliser des mesures des $az$ pour déterminer le câble non tendu il sera donc nécessaire de mesurer très précisément cet angle.

Pour cette mesure on pourrait penser à un système mécanique par qui mesure de combien tourne les câbles en $A$. Pour cela on peut utiliser une réglette qui tourne autour d'un axe horizontal passant par $A$, qui supporte un tube pouvant tourner autour d'un axe perpendiculaire au précédent par lequel passe le câble (figure 19).

Figure 19: La mesure des angles $ax$, $az$ d'un CDPR

La mesure des rotations autour des deux axes fournit les angles $ax$ et $az$. Toutefois l'expérience montre que ce genre de système ne se tournent qu'approximativement vers $B$ en raison des frottements mécaniques, en particulier pour les câbles soumis à peu de tension: l'erreur de mesure des angles peut atteindre 20 degrés et est donc bien trop importante pour déterminer le câble non tendu.

Un système optique est plus approprié puisqu'il n'influence pas l'angle $az$. Une caméra placée en $A$ peut être utilisée: dans l'image on peut repérer le câble et en déduite l'angle $az$. Toutefois cette mesure est sensible au condition d'illumination et sa précision décroît avec la taille du CDPR.

On peut aussi utiliser une autre approche qui utilise un capteur de distance de type télémètre laser monté sur une tête rotative et qui effectue une mesure de distance à intervalle régulier lors de la rotation: ces capteurs sont appelés des lidars. On obtient alors un nuage de point dans le repère du capteur. Il existe des lidars très coûteux qui font des mesures 3D mais il existe aussi des lidars qui se contentent de mesurer dans un plan pour une centaine d'euros (figure 20).

Figure 20: Deux lidars montés sur une charge. Ce sont les cylindres noirs sur les côtés du bidon. L'un mesure des distances dans un plan vertical, l'autre dans un plan horizontal.

La vidéo ci-dessous montre le fonctionnement d'un lidar. La tête rotative au centre émet une impulsion de lumière laser (la flèche rouge partant de la tête). Si le laser rencontre un obstacle (le point noir sur l'obstacle il y a réflection de la lumière vers la tête rotative (flèche rouge orientée vers la tête). La mesure du temps entre émission et réception multipliée par la vitesse de la lumière donne le double de la distance entre la tête et l'obstacle dans cette direction. On obtient ainsi une collection de point sur les obstacles (les cercles noirs sur les obstacles) dont on connaît les positions .

VIDEO

Nous verrons dans la section 10.1.8 comment faire un lidar à moindre coût. Un lidar est caractérisé par sa portée qui est la distance maximum à laquelle il peut détecter un obstacle et par une distance minimum (en dessous de cette distance il ne peut pas la mesurer). Dans le cas de la mesure des angles en $A$ il faut un lidar qui ait une distance minimum de l'ordre du centimètre et une portée de l'ordre de 30 cm. Lors de son balayage ce type de lidar va voir uniquement quelques points sur le câble car les obstacles en dehors du câble sont hors de portée. A partir de ces points et moyennant que l'on connaisse la position du lidar par rapport à $A$ et son orientation on peut calculer les angles $az$ et $ax$ en $A$. En plaçant un lidar proche de $B$ on pourra aussi mesurer les angles en $B$. Les tests ont montré que la précision de mesure était de l'ordre de 0.5 à 1 degré. Cette précision sur l'angle $az$ n'est pas suffisante pour faire la distinction entre les différentes positions de $B$ que l'on peut obtenir à partir des longueurs de câble. Par contre la mesure de $ax$ permettra de déterminer assez précisément si un câble est tendu ou non.

Une autre manière de mesurer l'angle $ax$ est d'utiliser un accéléromètre (figure 21). Ce capteur mesure l'accélération auquel le capteur est soumis dans trois directions de l'espace: deux dans le plan du capteur et une autour de la normale à ce plan.

Figure 21: Un accéléromètre 3D

A l'arrêt cette accélération est seulement celle due à la gravité donc est verticale. En mouvement il y a en plus l'accélération du mouvement mais on va supposer qu'elle est faible. On place l'accéléromètre parallèle au câble (sur la figure l'axe y). On peut alors montrer qu'avec la mesure le l'accéléromètre en x et y on peut calculer l'angle du câble avec l'horizontale. On peut mettre un tel dispositif non loin de $B$ de façon à ne pas gêner l'enroulement du câble. La précision de la mesure est de l'ordre de 0.5 à 1 degrés à l'arrêt mais de 2 à 8 degrés en mouvement.

Avec le dispositif ci-dessus on peut donc mesurer l'angle $ax$ en un point particulier du câble. Cela peut être suffisant pour détecter quel câble est détendu si l'estimation des longueurs des câbles est suffisamment précise pour avoir une bonne estimation des positions possibles de $B$, ce qui ne sera pas toujours le cas.

A noter que beaucoup de cartes électroniques incluent, outre l'accéléromètre, un gyromètre qui mesure la vitesse de rotation du capteur autour des mêmes axes que l'accéléromètre et un compas magnétique qui mesure l'angle entre l'axe du capteur et le nord magnétique.

9.3 Mesurer directement la position de $B$

Évidemment être capable de mesurer directement la position de $B$ avec une précision correcte serait un gros avantage: à partir de cette mesure on pourrait directement calculer la longueur des câbles en les supposant tendus sans avoir à passer par la mesure de la rotation des tambours. Remarquons toutefois que cela ne permet pas de savoir si un câble est tendu ou non.

9.3.1 La mesure de la hauteur

Si l'on suppose que le sol est plat, obtenir une estimation de la hauteur de $B$ n'est pas trop difficile. Il suffit par exemple de mettre un capteur de distance selon la verticale. Mais le capteur de distance est forcément en dessous de $B$ et sa mesure va donc être influencée par les oscillations de la charge.

Une solution plus robuste est de placer un lidar sur la charge, dont le rôle va être de mesurer non pas un point au sol mais plusieurs. Une opération mathématique simple permet alors non seulement d'estimer la hauteur de $B$ à quelques millimètres près mais aussi d'évaluer l'amplitude de l'oscillation de la charge autour d'un axe particulier. Pour cette mesure il n'est pas nécessaire d'avoir une rotation complète du lidar: une mesure de $\pm$ 5 degrés autour de l'axe du lidar est suffisante.

:

Un lidar placé sous la charge mesure la distance entre le centre du lidar et le sol selon plusieurs angles (figure 22).

Figure 22: La mesure de la hauteur de la charge

Pour chacun de ces points la distance et la direction sont mesurées. On a donc les coordonnées de ces points dans le repère $C , x_c , z_c$. Une régression linéaire permet de trouver la droite qui passe au mieux par ces points. L'équation de cette droite dans le repère $C , x_c , z_c$ s'écrit:

$$z_c = a x_c +b$$

$a$ est la pente de la droite et s'écrit $a = tan(u)$. On ramène cette droite dans le le repère $B x, z$ par une rotation d'angle $\theta$ de façon à ce que la pente de la nouvelle droite devienne nulle puisque le sol est horizontal. Il est facile de montrer que l'on a $\theta = -u$ et que la hauteur de $C$ par rapport au sol est $b \cos\theta$. On a mesuré préalablement la différence de hauteur $d$ entre $B$ et $C$ et la distance de $B$ au sol est donc $(d+b)\cos\theta$ et la charge a tourné d'un angle $\theta$ autour de l'axe $y$.

9.3.2 Mesurer la position $x, y$ de $B$

Pour faire fonctionner un CDPR on a défini des directions possibles de mouvement: haut/bas, gauche/droite, avant/arrière. Pour ces deux dernières directions cela veut dire que l'on a défini deux directions spécifiques, perpendiculaires l'une à l'autre, que l'on a appelle $x$ et $y$. On a aussi choisi un point particulier $O$ dans l'espace tel que l'on définit la position de $B$ par la distance entre $O$ et $B$ selon les deux axes $x$, $y$. Plus simplement imaginez une pièce carré ou on a placé $O$ au sol dans un des coins où deux murs perpendiculaires se rejoignent. L'axe $x$ part de $O$ et suit le pied d'un mur et l'axe $y$ part de $O$ et suit l'autre mur. Si l'on place un objet dans la pièce et que l'on mesure la distance de l'objet à chacun des murs on aura complètement localisé l'objet.

Imaginons maintenant que nous plaçons deux plaques planes verticales autour du CDPR dans une position connue, l'une perpendiculaire à $x$, l'autre à $y$ (dans notre pièce ces plaques peuvent être les deux murs $x$, $y$). Un lidar placé sur le support de la charge va mesurer des points sur ces plaques et une opération mathématique simple permet de déduire des mesures la distance de l'objet aux plaques, donc de mesurer la position de la charge.

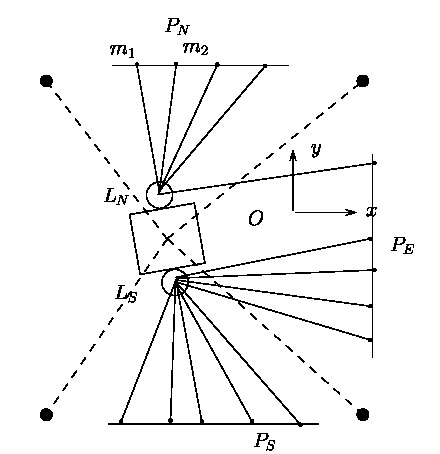
En pratique il est souhaitable d'en placer plus de deux car selon la position de la charge un lidar peut ne voir que très peu de points d'une des plaques, voire aucun. Sur la figure 23 on a placé 3 plaques verticales $P_N, P_E, P_S$ autour du CDPR, en dehors de la zone atteignable par $B$ et deux lidars $L_N, L_S$ placés de part et d'autre de $B$. Le lidar $L_N$ voit bien la plaque $P_N$ et mesure la position de points $m$ sur $P_N$ mais très peu de points sur $P_E$. Le lidar $L_S$ lui voit des points sur $P_E$ et $P_S$.

Figure 23: UN CDPR équipé de 2 lidars $L_N$, $L_S$ qui mesurent la position de points sur les plaques verticales $P_N$, $P_E$, $P_S$.

La vidéo suivante illustre ce principe dans une pièce avec 4 plaques. Sur la charge sont placés deux lidars, l'un $L_N$ au nord, l'autre $L_S$ au sud dans une position symétrique par rapport à $B$. On a volontairement réduit la vitesse de rotation des lidars et pris un grand pas pour leur rotation. On voit sur les plaques pendant la rotation des lidars les points identifiés par les lidars sur les plaques (en vert pour le lidar nord et en rouge pour le lidar sud). On voit clairement les instants où les lidars ne donnent pas de mesure en raison d'une occultation due à la charge ou lorsque la distance à un obstacle est supérieure à leur porté. Lorsque les lidars ont fait une rotation complète la charge se déplace. Dans la réalité la charge se déplace en permanence mais vu le temps faible d'acquisition des lidars (typiquement moins de 0.1 seconde) le déplacement de la charge pendant l'acquisition peut être négligé.

VIDEO

En utilisant la même technique que pour le lidar de hauteur on peut mesurer les coordonnées des centres $C_N$, $C_S$ des lidars dans le repère $O, x, y$. Les coordonnées de $B$ sont alors la moitiés de la somme des coordonnées de $C_N, C_S$.

Lors d'un déplacement la charge peut tourner autour de l'axe vertical. Cela ne perturbera le calcul des coordonnées de $B$ mais de plus, sans entrer dans les détails, les mesures lidar permettent aussi de mesurer de combien la charge a tourné.

En pratique un lidar bas coût a un pas de rotation de l'ordre de 0.45 degrés et l'on peut faire 3 rotations complètes en 0.1 seconde. Pour un CDPR qui se déplace à vitesse modérée (typiquement de quelques centimètres par seconde) on peut estimer que le changement de position de $B$ en 0.1 seconde est suffisamment faible pour être négligé. Si les plaques sont suffisamment longues et bien visibles par les lidars on obtiendra alors un nombre important de points de mesure et donc une bonne précision pour la localisation de $B$. Les tests avec les lidars présentés sur la figure 20 ont montré que l'on pouvait atteindre un précision de positionnement de l'ordre de 1 à 2 centimètres.

: Soit $C_N$, $C_S$ les centres des lidar $L_N$, $L_S$. On suppose que $B$ est au milieu de $C_NC_S$, $d$ étant la distance entre $C_N$ et $C_S$ (figure 24).

Figure 24: Comment mesurer la rotation de la charge avec les mesures lidar.

La mesure des lidars des points sur les les plans $P_N$, $P_S$ fournit les coordonnées $y_N$, $y_S$ de $C_N$, $C_S$ alors que la mesure de $L_S$ fournit la coordonnée selon $x$ de $C_S$, dont on déduit les distances $d_1$ de $C_S$ à $P_E$ et $d_2$ de $B$ à $P_E$. Soit $\theta$ l'angle de la rotation autour de la verticale de la charge. On a

$$\vert y_N-Y_S\vert d \cos \theta ~~~~~ d_2-d_1 =\frac{d \sin(\theta)}{2}$$

ce qui permet de calculer $\theta$.

9.4 Combiner mesure d'angle et de position de $B$

Nous avons vu que pour déterminer parfaitement la forme d'un câble il faut avoir 3 informations sur celui-ci. Nous allons étudier comment on peut combiner les mesures décrites dans les sections précédentes pour détecter les câbles non tendus et estimer la longueur réelle du câble.

9.4.1 Combiner mesure de hauteur et de deux angles

On va supposer qu'un lidar nous fournit la hauteur de $B$, un autre l'angle $ax$ du câble en $A$ et qu'un autre dispositif l'angle $ax$ soit en $B$ (lidar) où en un point à distance connue de $B$ (accéléromètre par exemple). Une transformation mathématique complexe permet alors de déterminer la longueur du câble, sa forme ainsi que la position de l'extrémité du câble dans le plan vertical qui contient le câble. A partir de ces informations on peut donc obtenir à la fois la position de $B$ et déterminer quels sont les câbles tendus. Toutefois ces calculs sont très sensibles aux erreur de mesure et nos tests ont montré qu'avec les incertitudes que nous avons sur les mesures ces calculs ne donnaient pas de bons résultats.

: Supposons que nous avons la hauteur $z_B$ de $B$ et les mesures $a_1, a_2$ de la pente du câble en deux points de celui ci, pente qui est la tangente de l'angle $u$ entre le câble en ce point et l'axe horizontal. Le premier cas à traiter est quand les pentes sont approximativement identiques, ce qui implique que le câble est tendu. La longueur $L$ du câble est alors $z_B/\sin{u}$. Si à l'opposé $a_1, a_2$ sont sensiblement différents alors le câble est détendu. Mais nous savons que la position de $B$ peut être uniquement déterminé à partir de la longueur des câbles tendus. Pour la forme et la longueur des câbles détendus la mesure de la pente en un point du câble permet d'exprimer, par exemple, $F_z$ en fonction de $F_x, L$ et de la valeur de la pente. Connaissant $x_B, z_B$ les 2 équations (10, 11) n'ont comme inconnues que $F_x, L$ et peuvent être résolues numériquement pour donner la longueur du câble. Si un câble est détendu et qu'on utilise la stratégie de continuité pour gérer le CDPR, la stratégie de commande pour ne pas avoir de câble(s) trop détendu(s) va être d'ajuster la vitesse de rotation du tambour. Si la vitesse et la direction de la charge est fixée et que le câble est tendu, alors on sait calculer une vitesse nominale pour le câble. Si le câble n'est pas tendu on va ajuster la vitesse autour de la vitesse nominale pour réduire l'écart entre la longueur du câble et la version tendu. On peut ajuster la vitesse des tambours en utilisant soit la différence entre $L$ et la longueur du câble tendu, soit la différence entre $a_1$ et $a_2$, ce qui ne nécessite pas le calcul de $L$. Le choix entre ces deux solutions va dépendre de l'amplitude des erreurs de mesure sur $a_1$, $a_2$. Si sur la trajectoire suivie le câble doit s'allonger on va simplement ralentir son déroulement d'un facteur proportionnel à cette différence. Si au contraire le câble doit s'enrouler on va au contraire augmenter sa vitesse d'enroulement de ce facteur.

9.4.2 La voie royale: les 3 lidars

On a vu qu'avec 2 lidars horizontaux, 3 plans de référence et un lidar pour mesurer la hauteur on pouvait obtenir une bonne estimation de la position de $B$. Avec cette estimation on obtient 2 informations pour déterminer la forme ces câbles. Il suffit d'une troisième information (par exemple l'angle $ax$ pour un point du câble proche de $B$) pour obtenir la forme du câble. Il devient simple de savoir si un câble est tendu ou non et d'avoir le moyen de contrôler qu'un câble non tendu ne se détend pas trop. En effet connaissant la position de $B$ on peut calculer exactement l'angle $ax$ si le câble est tendu. S'il ne l'est pas on a une mesure de la déviation de longueur par la différence entre l'angle tendu et la mesure. Une autre approche serait de reconstruire la longueur du câble (ce qui n'est pas une mince affaire) et de travailler sur la différence longueur de câble si tendu et longueur estimée. Toutefois la différence angulaire aura, en général, une amplitude plus importante que la différence de longueur lorsque l'on est prés de la situation tendue. Ceci est montré sur le film suivant où partant de la longueur tendu on allonge le câble. L'allongement du câble est montré en bleu alors que l'angle est montré en rouge.

VIDEO

L'utilisation de la différence angulaire t constitue donc un meilleur choix pour l'ajustement de vitesse décrit dans la section précédente.

9.5 Mesurer les oscillations et la rotation de la charge

Nous avons vu que les lois de la mécanique imposent que la charge va osciller durant les mouvements d'un CDPR. Sans être trop technique on sait que la charge peut osciller de trois manières (faites une recherche sur le web avec les mots roulis/tangage/lacet par exemple) en utilisant trois angles. Sans entrer dans les détails si vous placez un accéléromètre en $B$ et que vous supposez qu'il est simplement soumis à la gravité verticale, alors vous ne pourrez mesurer que deux de ces trois angles. Par exemple supposez que le capteur est horizontal et que la charge tourne simplement autour de la verticale à vitesse constante (donc l'accélération autour de l'axe vertical est nulle): le capteur donnera alors toujours la même mesure, qui indique la direction de la gravité et ne permettra donc pas d'évaluer la rotation.

Nous avons cependant vu l'utilisation des lidars pour la détermination de la position sur les axes $x$, $y$ permettait la détermination de cette rotation tandis que le lidar mesurant la hauteur permettait d'estimer la rotation autour d'une axe horizontal. Si vous ne disposez pas de ces lidars il existe une solution: beaucoup d'accéléromètre mesure, outre les accélérations, la direction du nord magnétique via un compas magnétique. La rotation de la charge va alors induire un changement dans la direction du nord et ce changement vous donnera approximativement la rotation de la charge. Il est cependant impératif de ne pas avoir à proximité de la charge des masses métalliques importantes et de ne pas mettre à proximité du capteur des éléments électriques, comme un moteur, car ce sont des éléments qui créent un champ magnétique qui peut être très largement supérieur à celui du nord magnétique et vont donc considérablement perturber la mesure du compas. Sous cette hypothèse nos tests ont montré que l'on pouvait mesurer la rotation de la charge avec une erreur maximale de l'ordre de deux à trois degrés.

Une autre possibilité est l'utilisation du gyromètre qui mesure les vitesses de rotation autour des trois axes. Toutefois pour obtenir l'amplitude des rotations il va falloir procéder à une opération mathématique appelée intégration numérique qui permet de remonter de la vitesse de rotation à l'amplitude de la rotation. Malheureusement si la mesure du gyromètre n'est pas très précise l'estimation des rotations va rapidement s'écarter de leurs véritables valeurs.