An Individual-based model simulator for clonal plant growth developed in 2011 and 2012 in the context of the ANR Syscom project Modecol, in Matlab.
Context
It was developed within the ANR Syscomm (SYStèmes Complexes et Modélisation Mathématique) project MODECOL ( MODélisation ECOLogique de prairies virtuelles) [ANR-08-SYSC-012]. The model presented here is detailed and analyzed in: F. Campillo and N. Champagnat, Simulation and analysis of an individual-based model for graph-structured plant dynamics, Ecological Modeling 2012. [PDF].
Description
We propose a stochastic individual-based model of graph-structured population, viewed as a simple model of clonal plants. The dynamics is modeled in continuous time and space, and focuses on the effects of the network structure of the plant on the growth strategy of ramets. This model is coupled with an explicit advection-diffusion dynamics for resources.
At time ![]() clonal plant is represented as a set of nodes (ramets) that may be connected by links (rhizomes or stolons). In this simplified representation of a clonal plant, ramets are represented by points in the plane, and connection by lines. The state of the nodes is described by the following finite measure:
clonal plant is represented as a set of nodes (ramets) that may be connected by links (rhizomes or stolons). In this simplified representation of a clonal plant, ramets are represented by points in the plane, and connection by lines. The state of the nodes is described by the following finite measure:
![Rendered by QuickLaTeX.com \[\nu_t=\sum_{i=1}^{N_t}\delta_{x^i_t}\]](../../wp-content/ql-cache/quicklatex.com-5f174943249756da52d4f10142c0b874_l3.png)
where
![]()
The plant grows in a resource landscape. At each time ![]() , this resource landscape is represented by
, this resource landscape is represented by ![]() the available resources at position
the available resources at position ![]() . The nodes accessing high levels of resources
. The nodes accessing high levels of resources ![]() are more likely to give birth to new nodes.
are more likely to give birth to new nodes.
Birth and death rates
Each node of ![]() in position
in position ![]() may disappear at a death rate
may disappear at a death rate ![]() and give birth to a new node at a birth rate
and give birth to a new node at a birth rate ![]() . These rates are per capita rates. Global death and birth rates at population level are respectively:
. These rates are per capita rates. Global death and birth rates at population level are respectively: ![]() and
and ![]() ; the global event rate is
; the global event rate is ![]() . Basically, the per capita rates depend on the local availability of resources: we suppose that the birth rate
. Basically, the per capita rates depend on the local availability of resources: we suppose that the birth rate ![]() is an increasing function of
is an increasing function of ![]() and the death rate
and the death rate ![]() is a decreasing function of
is a decreasing function of ![]() . When a node is added to the population, it is always linked with the mother node; when a node
. When a node is added to the population, it is always linked with the mother node; when a node ![]() is removed from population, all connections to
is removed from population, all connections to ![]() are suppressed.
are suppressed.
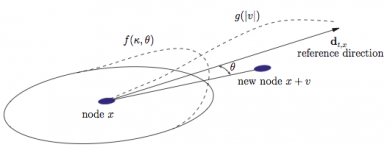
Dispersion kernel
A node at position ![]() at time
at time ![]() gives birth to a new node at position
gives birth to a new node at position ![]() according to the p.d.f.
according to the p.d.f. ![]() .
. ![]() is the angle between the preferred direction of reference
is the angle between the preferred direction of reference ![]() and the direction of the new shoot
and the direction of the new shoot ![]() .
. ![]() is the p.d.f. of the angle of the new shoot and
is the p.d.f. of the angle of the new shoot and ![]() is the p.d.f. of the length of the associated link.
is the p.d.f. of the length of the associated link. ![]() will be a rough approximation of the gradient of
will be a rough approximation of the gradient of ![]() given by connected nodes.
given by connected nodes.
Interactions between nodes and resources
For the coupling of the (discrete) individual dynamics with the resource density dynamics ![]() is modeled as:
is modeled as:
(![]() )
) ![Rendered by QuickLaTeX.com \[\partial_t \mathbf{r}(t,x)=\textrm{div}(\mathbf{a}(x),\nabla \mathbf{r}(t,x))+\mathbf{b}(x)\cdot\nabla \mathbf{r}(t,x)-\alpha,\mathbf{r}(t,x),\sum_{i=1}^{N_t} \Gamma_{x^i_t}(x) <!-- /wp:paragraph --> <!-- wp:paragraph --> \]](../../wp-content/ql-cache/quicklatex.com-42d5d29019702d1bcf39a474788eda2d_l3.png)
we model with the kernel ![]() the fact that resource consumption is not local.
the fact that resource consumption is not local.
Exact Monte Carlo simulation of the IBM
The only approximation is the numerical integration of the resource dynamics ![]() which is performed with a finite difference scheme.
which is performed with a finite difference scheme.
,
,
given for
do compute the rate
and
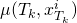
,
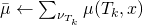
with
if
then sample
according to
sample
according to
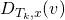
[birth] else sample
according to
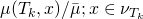
end if compute
[numerical approximation of
] end for
Simulation
Here the angle p.d.f. ![]() is a Von Mises distribution of parameters
is a Von Mises distribution of parameters ![]() and
and ![]() ; the length p.d.f.
; the length p.d.f. ![]() is a log-normal distribution of parameters
is a log-normal distribution of parameters ![]() and
and ![]() The maximum link per node is
The maximum link per node is ![]() .
.
Guerilla
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() :
:
Phalanx
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() :
:
