Next: Other problems: inequalities, parametric Up: benches Previous: Optimization

La page de J-P. Merlet

J-P. Merlet home page

La page Présentation de HEPHAISTOS

HEPHAISTOS home page

La page "Présentation" de l'INRIA

INRIA home page

Subsections

Integration

Abs-Exp

Origin:Quateroni A, Sacco, R. and Saleri, F., Numerical mathematics, Springer 2000, pp. 413

Compute

$\begin{displaymath} \int_{-1}^{1}\vert x\vert e^{x} dx \end{displaymath}$

The result is a range with width lower than $\epsilon$ that includes the value of the integral.

Method: IntegrateRectangle or IntegrateTaylor
Solutions::[1.2642411126774618, 1.2642411226375476] ( $\epsilon=1e-8)$
Computation time (February 2006):

DELL D400 (1.7Ghz)

0.019s (Rectangle) 0.004 (Taylor)

comp.soft-sys.math.maple18257

Origin: Article 18257 of comp.soft-sys.math.maple

Compute

$\begin{displaymath} \int_0^{2\pi} e^(\cos(x))\cos(x-\sin(x)) dx \end{displaymath}$

Method: IntegrateTaylor
Solution: [6.2831848095217104, 6.2831858068365776] ( $\epsilon=1e-6)$
Solution:[6.2831853021819217, 6.2831853121792607] ( $\epsilon=1e-8)$
Computation time (Mars 2006):

DELL D400 (1.7Ghz), Taylor order: 3	0.22s ( $\epsilon=1e-6$ ), 1.35s ( $\epsilon=1e-8$ )
DELL D400 (1.7Ghz), Taylor order: 4	0.09s ( $\epsilon=1e-6$ ), 0.21s ( $\epsilon=1e-8$ )
DELL D400 (1.7Ghz), Taylor order: 5	0.09s ( $\epsilon=1e-6$ ), 0.18s ( $\epsilon=1e-8$ )
DELL D400 (1.7Ghz), Taylor order: 6	0.07s ( $\epsilon=1e-6$ ), 0.18s ( $\epsilon=1e-8$ )

Ellipsoid

Origin:Quateroni A, Sacco, R. and Saleri, F., Numerical mathematics, Springer 2000, pp. 410-412

Compute

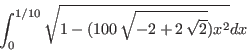
$\begin{displaymath} \int_0^{1/10}\sqrt{1-(100\,\sqrt {-2+2\,\sqrt {2}})x^2}dx \end{displaymath}$

The result is a range with width lower than $\epsilon$ that includes the value of the integral.

Method: IntegrateRectangle
Solution: [.081356291802596431, .081357224879917173] ( $\epsilon=1e-6$ )
Solution: [0.081356786414213011, 0.081356796338971332] ( $\epsilon=1e-8$ )
Computation time (February 2006):

DELL D400 (1.7Ghz)

0.001s ( $\epsilon=1e-6$ ), 0.002s ( $\epsilon=1e-8$ )

Sail boat

Origin:Quateroni A, Sacco, R. and Saleri, F., Numerical mathematics, Springer 2000, pp. 410-412

Compute

$\begin{displaymath} \int_0^{10} \frac{\alpha x e^{-\gamma x}}{x+\beta} dx \end{displaymath}$

with $\alpha =50$ , $\beta =5/3$ , $\gamma = 1/4$ . The result is a range with width lower than $\epsilon$ that includes the value of the integral.

Method: IntegrateRectangle
Solution: [100.06136781918083, 100.06136881760561] ( $\epsilon=1e-6)$
Solution:[100.06136831296580, 100.06136832296060] ( $\epsilon=1e-8)$
Computation time (February 2006):

DELL D400 (1.7Ghz)

0.0457s ( $\epsilon=1e-6$ ), 0.886s ( $\epsilon=1e-8$ )

sci.math.num-analysis89520

Origin: Article 89520 of sci.math.num-analysis

Compute

$\begin{displaymath} \int_0^{\pi} \sqrt{1-cos^2(x)} dx \end{displaymath}$

Method: IntegrateTaylor
Solution: [1.99999527,2.0000004987] ( $\epsilon=1e-6)$
Solution:[1.999999995087,2.0000000050096] ( $\epsilon=1e-8)$
Computation time (Mars 2006):

DELL D400 (1.7Ghz)

0.62s ( $\epsilon=1e-6$ ), 1.33s ( $\epsilon=1e-8$ )

sci.math.num-analysis.91892

Origin: Article 91892 of sci.math.num-analysis
with

 
k = 400 * Pi / 3
a = 3.75E-6
q = 0.000875
d1 = k*R * (3*a^2 - 2*R^2)
d2 = 2*R^2 + a^2 * (k^2 * R^2 - 3)
R = sqrt(a^2 + (q-z)^2)
P = 0.005 / (0.17708 * 8*Pi^2*R^5

Compute

$\begin{displaymath} \int_{0.0025}^{0.0025} (P\cos(600\pi~)(d2\cos(kR)-d1\sin(kR)) \end{displaymath}$

Method: IntegrateTaylor
Solution: [886.6380446722454,886.6380456712287] ( $\epsilon=1e-6)$
Method: IntegrateTaylor at order

Computation time (August 2006):

DELL D400 (1.7Ghz)

164.24s (

)

71.28s (

)

stoutemyer2007

Origin: [12]

Compute

$\begin{displaymath} \int_{0}^{1} log((exp(x)+2\sqrt{x}+1)/2.) \end{displaymath}$

Method: IntegrateTaylor
Solution: [0.67637670822541165607681348942, 0.67637670822543264594435536661], ( $\epsilon=2.1e-14)$
Method: IntegrateTaylor at order