next up previous Next: Integration Up: benches Previous: Non-polynomial systems

  • La page de J-P. Merlet
  • J-P. Merlet home page
  • La page Présentation de HEPHAISTOS
  • HEPHAISTOS home page
  • La page "Présentation" de l'INRIA
  • INRIA home page

    Subsections

    Optimization

    Branin

    Origin: [5]
    Minimize

    \begin{displaymath} 10+\left ({\it x2}- 0.12918450914398065859\,{{\it x1}}^{2}+ ... ...{\it x1}-6\right )^{2}+ 9.6021126422702616606 \,\cos({\it x1}) \end{displaymath}

    for $x1$ in [-5,10], $x2$ in [10,15]

    Method: MinimizeGradient
    Solutions:: 1 (approximate): [0.40071578316961798, 0.40071578316963219]
    Computation time (September 2006):

    DELL D400 (1.7Ghz) 0.01s

    Eisenberg

    Origin: Maple news group
    Maximize

    \begin{displaymath} \left \vert 0.592\,{\frac {x\left ({e}-1\right )}{\left (- 0.408\,x+1\right )\left ({e^{x}}-1\right )}}-1\right \vert \end{displaymath}

    for x in the range [0.5,0.8]

    Method: Maximize
    Solutions:: 1 (approximate)[0.017165175414059930, 0.017165175414062483]
    Computation time (January 2005):

    Sun Blade 7.3s

    Goldstein-Price

    Origin: [5]
    Let

    \begin{displaymath} a = 1+\left ({\it x1}+{\it x2}+1\right )^{2}\left (19-14\,{\... ...-14\,{\it x2}+6\,{\it x1}\,{\it x2}+3\,{{\it x2}}^{2} \right ) \end{displaymath}


    \begin{displaymath} b=30+\left (2\,{\it x1}-3\,{\it x2}\right )^{2}\left (18-32\... ...\it x1}}^{2}+75\,{{\it x2}}^{2}-36\,{\it x1}\,{\it x2}\right ) \end{displaymath}

    and the function to be minimized:

    \begin{displaymath} f=a b \end{displaymath}

    where all $x_i$ are in [-2,2]

    Method: MinimizeGradient
    Solutions:: 1 (approximate): [-2848.8726372535571, -2848.8726372535311]
    Computation time (September 2006):

    DELL D400 (1.7Ghz) 0.86s

    Klein

    Origin:klein@mathematik.uni-kassel.de
    Minimize

    \begin{displaymath} Y(j+1)(2-2Y) \end{displaymath}

    subject to the constraint:

    \begin{displaymath} -Ylog[2](Y)-(1-Y)log[2](1-Y)-(1-0.75j/(j+1))=0 \end{displaymath}

    where $log[2]$ mean log in base 2 (i.e. $log[2](x)=ln(x)/ln(2)$)

    Range: j=[0,1], Y=[0.01,0.99]

    Method: MinimizeGradient
    Solutions:: 1 (approximate): 0.498776
    Computation time (April 2003):

    Sun Blade 1mn24s

    Klein1

    Origin:klein@mathematik.uni-kassel.de
    Minimize

    \begin{displaymath} Y(j+1)(2-2Y) \end{displaymath}

    subject to the constraint:

    \begin{displaymath} -Ylog[2](Y)-(1-Y)log[2](1-Y)-(1-r~j/(j+1))=0 \end{displaymath}

    where $log[2]$ mean log in base 2 (i.e. $log[2](x)=ln(x)/ln(2)$)

    Range: j=[0,1], Y=[0.01,0.99], r=[0,1]

    Method: MinimizeGradient
    Solutions:: 1 (approximate): .39171414594587
    Computation time (April 2003):

    Sun Blade 1mn55s

    MaxCylinder

    Origin: COPRIN
    Physical meaning: for a robot with 3 degree of freedom $x,y, \phi$ a function $F$ defines a singularity variety in which the robot cannot be controlled. We are looking for the maximal disc centered at a given point of coordinates $x_0, y_0$, such that the disc has not intersection with the singularity variety for any orientation in the range [-a,a]. The orientation may thus be written as $T=a \sin\alpha$ and the singularity variety is $F(x,y,\alpha)$, The problem is solved with a Lagrange multiplier $\lambda$ by writing

    \begin{displaymath} H=(x-x_0)^2+(y-y_0)^2+\lambda F \end{displaymath}

    The derivatives of $H$ with respect to $x, y$ are combined to eliminate $\lambda$. The optimality equations constitute then a system of 3 equations in $x, y, \alpha$. The roots $x_r, y_r$ of this system are used to calculate $(x_r-x_0)^2+(y_r-y_0)^2$ and the lowest value of this quantity is the square of the largest singularity-free disc.

    The 3 equations to solve are: 

     
-13626.359958*x-17242.663338*y+306.1030*y^2*sin(alpha)^4+1224.4120*y*sin(alpha)^3*x
-327743.551830*sin(alpha)^4-2623771.960340*sin(alpha)^3+561700.662040*sin(alpha)^2
-306.1030*x^2*sin(alpha)^4-1680682.162260*sin(alpha)+182179.510990-1256.4908*x^2*sin(alpha)^3+
1256.4908*y^2*sin(alpha)^3+1256.4908*y*x-48283.435536*x*sin(alpha)^2-16255.087100*y*sin(alpha)^2
+306.1030*x^2-8129.699104*y*sin(alpha)+1224.4120*y*sin(alpha)*x-69790.833024*y*sin(alpha)^3
-306.1030*y^2-1256.4908*sin(alpha)*x^2+129340.554748*sin(alpha)*x+151105.785340*sin(alpha)^3*x+
1256.4908*sin(alpha)*y^2+22752.806830*y*sin(alpha)^4
-1256.4908*y*x*sin(alpha)^4+27004.058342*x*sin(alpha)^4 =0

-4*(x-15)*cos(alpha)*(942.3681*sin(alpha)^2*x*y-19159.084776*x-15238.646187*y+306.1030*y*sin(alpha)^3*x
+40242.36852580*sin(alpha)^3+197386.15916499*sin(alpha)^2-66170.43895050*sin(alpha)+
1857.6978*sin(alpha)^2*x^2+172248.32737589-246.6856*x^2*sin(alpha)^3+381.5598*y^2*sin(alpha)^3+
314.1227*y*x-103723.104768*x*sin(alpha)^2-62039.861505*y*sin(alpha)^2+619.2326*x^2+
24141.717768*y*sin(alpha)-27346.225342*y*sin(alpha)^3+466.1811*y^2-8127.543550*sin(alpha)*x+
8244.982830*sin(alpha)^3*x+1398.5433*sin(alpha)^2*y^2) = 0

-1367.419669*x+6984.263479*y+190.7799*y^2*sin(alpha)^4+628.2454*y*sin(alpha)^3*x+
20121.18426290*sin(alpha)^4+131590.77277666*sin(alpha)^3-66170.43895050*sin(alpha)^2
-123.3428*x^2*sin(alpha)^4+344496.65475178*sin(alpha)+1238.4652*x^2*sin(alpha)^3+
932.3622*y^2*sin(alpha)^3-153.0515*y*x-29221.45558380-8127.543550*x*sin(alpha)^2+
24141.717768*y*sin(alpha)^2+123.3428*x^2-30477.292374*y*sin(alpha)+628.2454*y*sin(alpha)*x
-41359.907670*y*sin(alpha)^3-190.7799*y^2+1238.4652*sin(alpha)*x^2-38318.169552*sin(alpha)*x
-69148.736512*sin(alpha)^3*x+932.3622*sin(alpha)*y^2-13673.112671*y*sin(alpha)^4+
153.0515*y*x*sin(alpha)^4+4122.491415*x*sin(alpha)^4 = 0
    the last one being the singularity condition.

    Method: GradientSolve+ a specific simplification procedure that allow to avoid determining roots leading to a largest disc than the minimal one already computed
    Solutions:: 1
    Computation time (August 2004):

    DELL D400 (1.7Ghz) 2s

    O32

    Origin: COCONUT
    Minimize 
    37.293239 * x1 + 0.8356891 * x5 * x1 + 5.3578547 * x3^2 - 40792.141
    subject to the constraints: 
    -0.0022053 * x3 * x5 + 0.0056858 * x2 * x5 + 0.0006262 * x1 * x4-6.665593 <= 0
-0.0022053 * x3 * x5-0.0056858 * x2 * x5 - 0.0006262 * x1 * x4 -85.334407 <= 0
0.0071317 * x2 * x5 + 0.0021813 * x3^2 + 0.0029955 * x1 * x2 - 29.48751 <= 0
- 0.0071317 * x2 * x5 - 0.0021813 * x3^2 - 0.0029955 * x1 * x2 + 9.48751 <= 0
0.0047026 *x3 * x5+0.0019085 * x3 * x4 + 0.0012547 * x1 * x3 - 15.699039 <= 0
- 0.0047026 *x3 * x5 - 0.0019085 * x3 * x4 - 0.0012547 * x1 *x3+10.699039 <= 0
    Method: Minimize+3B Solutions:: 1, [-30665.538622963180, -30665.538622963169]
    Computation time (August 2004):
    DELL D400 (1.7Ghz) 2.04s

    Rastrigin

    Origin: [5]
    Minimize

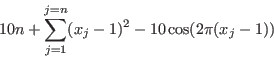
    \begin{displaymath} 10n+\sum_{j=1}^{j=n}(x_j-1)^2-10\cos(2\pi(x_j-1)) \end{displaymath}

    for $x_i$ in [-5.12,5.12], $n=10$

    Method: MinimizeGradient
    Solutions:: 1 (approximate): [0.10660130733697315e-6 , 0.10660157556685590e-6]
    Computation time (September 2006):

    DELL D400 (1.7Ghz) 0.7s ($n$=5), 2.07s ($n$=10)

    Rastrigin modified

    Origin: [5]
    Minimize

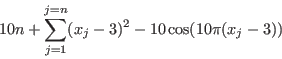
    \begin{displaymath} 10n+\sum_{j=1}^{j=n}(x_j-3)^2-10\cos(10\pi(x_j-3)) \end{displaymath}

    for $x_i$ in [-5.12,5.12], $n=10$

    Method: MinimizeGradient
    Solutions:: 1 (approximate): [0.000031981289218663278, 0.000031981289456695094]
    Computation time (September 2006):

    DELL D400 (1.7Ghz) 0.48s ($n$=5), 2.71s ($n$=10)

    Rosenbrock

    Origin: [5]
    Minimize

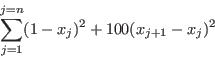
    \begin{displaymath} \sum_{j=1}^{j=n}(1-x_j)^2+100(x_{j+1}-x_j)^2 \end{displaymath}

    for $x_i$ in [-5.2,5.2], $n=15$

    Method: MinimizeGradient
    Solutions:: 1 (approximate): [0.000082898124320647843, 0.000082898124321706214]
    Computation time (September 2006):

    DELL D400 (1.7Ghz) 0.85s ($n$=5), 2.22s ($n$=10), 278s ($n$=15)

    Shekel

    Origin: [5]
    Let $A$ be:

    \begin{displaymath} \left [\begin {array}{cccc} 4&4&4&4\\ 1&1&1&1\\ 8&8&8&8\\ ... ...&9\\ 8&1&8&1\\ 6&2&6&2\\ 7& 3.6&7& 3.6 \end {array}\right ] \end{displaymath}

    and $c$:

    \begin{displaymath} \left [\begin {array}{c} 0.1\\ \noalign{\medskip } 0.2 \\ \n... ...{\medskip } 0.5\\ \noalign{\medskip } 0.5\end {array}\right ] \end{displaymath}

    and the function to be minimized:

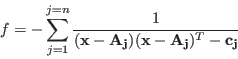
    \begin{displaymath} f= - \sum_{j=1}^{j=n} \frac{1}{({\bf x}-{\bf A_j})({\bf x}-{\bf A_j})^T-{\bf c_j}} \end{displaymath}

    where ${\bf A_j}$ is the $j-th$ row of ${\bf A}$ and all $x_i$ are in [0,10]

    Method: MinimizeGradient
    Solutions:: 1 (approximate) (-10.536409816178930, -10.536409816178907)
    Computation time (September 2006):

    DELL D400 (1.7Ghz) 0.31s ($n$=5), 1.66s ($n$=7), 2.61s ($n$=10)

    Shubert

    Origin: [5]
    Minimize

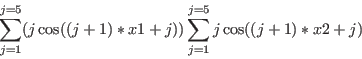
    \begin{displaymath} \sum_{j=1}^{j=5}(j\cos((j+1)*x1+j))\sum_{j=1}^{j=5}j\cos((j+1)*x2+j) \end{displaymath}

    for $x1$ in [-10,10], $x2$ in [-10,10]

    Method: MinimizeGradient
    Solutions:: 1 (approximate): [-186.73090883102699, -186.73090883102313]
    Computation time (September 2006):

    DELL D400 (1.7Ghz) 23.3s

    Six hump camel

    Origin: [5]
    Minimize

    \begin{displaymath} \left (4- 2.1\,{{\it x1}}^{2}+ {{\it x1}}^{4}/3 \right ){{\i... ...}\,{\it x2}+\left (-4+4\,{{\it x2}}^{2} \right ){{\it x2}}^{2} \end{displaymath}

    for $x1$ in [-3,3], $x2$ in [-2,2]

    Method: MinimizeGradient
    Solutions:: 1 (approximate): [-1.0316284534898656, -1.0316284534898621]
    Computation time (September 2006):

    DELL D400 (1.7Ghz) 0.96s

    Tf12

    Origin: COCONUT
    Minimize 
    x1+0.5*x2+x3/3.
    subject to, for i from 0 to M 
    -x1-i*h*x2-(i*h)^2*x3+tan(i*h) <= 0
    with h=1/M

    Method: Minimize+3B Solutions:: 1: [0.64903470935309138, 0.64903470935309149]
    Computation time (August 2004):

    DELL D400 (1.7Ghz) 60s

    next up previous Next: Integration Up: benches Previous: Non-polynomial systems
  • J-P. Merlet home page
  • La page Présentation de HEPHAISTOS
  • HEPHAISTOS home page
  • La page "Présentation" de l'INRIA
  • INRIA home page

    jean-pierre merlet