INRIA home page
The HEPHAISTOS examples page
Most of the problems presented in this document have been submitted to the
ALIAS-C++
library
through the ALIAS-Maple
library, a
software developed in the COPRIN project. A problem with
the prefix AOL has been submitted to the on-line solver
available at the home page of the COPRIN project.
Some of these problems have been solved using Maple procedures based on
the intpakX package:
http://www.math.uni-wuppertal.de/~xsc/software/intpakX/d_l_c.html
i.e. the multi-precision interval arithmetic library developed at the
Department of Mathematics and Computer Science, University of
Wuppertal.
This page has test examples for the following problems:
- polynomial system solving
- non polynomial system solving
- optimization problems
- miscellaneous problems: parametric polynomials, inequalities,...
In the last section 6 problems
that are considered to be
difficult: here difficult means that the computation time for a system
with a fixed number of unknowns on a single computer is larger than
10mn or, if the number of equations is variable, that the computation
time is larger than 10mn for a system with 10 equations.
Warning:
- Complexity: some systems are dependent upon an integer
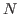whose value
indicates the complexity of the system. In that case
computation
times for various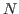 
are given in the corresponding section.
- System Naming: a given system admits various
mathematically equivalent forms (that may be
obtained for example by
combining the equations) but in terms of interval analysis these
systems are not equivalent as the solving time is heavily dependent
upon the form that is provided to the solver. In this document the naming is done according to
the following rules:
- the generic name of the system: the
system that is solved is exactly the one described in the reference
- the generic name of the system with a version number: the
system that is solved is a variant of the original system (which is
usually simpler to solve)
Therefore a system name is defined by its generic name, its version
and eventually its complexity.
It is important to mention that the equations that are presented in a
section are exactly the
one that are solved without any
pre-processing (except maybe for a
conversion into Horner form). For comparison purposes you need
therefore to solve the problem as it is presented without any change
- Exact solutions: in this document exact solution implies that the algorithm was
able to determine that there was a unique solution within some ranges
for the unknowns, solution that can be safely computed with an
iterative scheme up to an arbitrary accuracy. In the example the
solution are computed so that the residu of the equations is
1e-6. Note that usually provided the result of the C++ ALIAS program,
ALIAS Maple will then be able to calculate the roots with an arbirary accuracy.
- Solving procedure: name of methods indicated in typewriter font refers to procedure
of the ALIAS maple library.
- Computation times: they indicate the solving time of the
C++ code generated
by the ALIAS Maple interface without any processing of the generated C++
code and with standard settings for the solving parameters. We just
allow a choice in the solving procedure among the various solvers
provided by ALIAS-Maple. As for the filtering heuristics (such as 2B,
3B,...) we allow only the one implemented in ALIAS-Maple and most
of the time we use the same heuristics. Hence they
are indicative only as a specific treatment of the
equations or fine tuning of the solving parameters
will in many cases allows to decrease drastically the
solving time. Hence the presented solving times do not fully reflect
what maximal performance can be obtained with interval
analysis for a specific system. Different computation times may be indicated corresponding to
progress in the ALIAS solvers
- Solutions set: computation times are indicated for finding all the
solutions of the systems within the indicated search space. In most
cases the solutions are certified (denoted exact in the
examples) i.e.:
- for equations systems we have found an interval for the
unknowns in which we can guarantee that there is one and only
one solution, solution that we
can compute with an arbitrary accuracy (the computation time includes
the computation of the solution with an accuracy that is usually 1e-6)
- for optimization problems we have found an approximation
of the global extrema such that the distance between approximation and
the extrema is less than a given threshold (usually 1e-6)
This page is frequently updated either with new examples or with
improvements in the ALIAS computation time.
Contact: Jean-Pierre.Merlet@sophia.inria.fr
Updated on: October 4, 2017
Number of examples: 132
Next: Polynomial systems