Solution à base de contexte   Analyse du problème

Sous-sections

• La détection
• L'approche vitesse
• L'approche région
• L'extraction de primitives
• Bilan
• La reconnaissance
• Les modèles d'apparence d'objets
• Les modèles d'objets réels
• Bilan
• L'appariement temporel et le suivi
• La mise en correspondance
• Le filtre de Kalman
• Bilan
• Les conclusions

État de l'art

Le traitement de séquences d'images pour le suivi de personnes est un problème réel qui légitime son unité autant sur le plan théorique que sur le plan applicatif en ceci qu'il cherche à reconstituer par le calcul les évolutions d'une scène donnée au cours du temps. Malgré cela sa résolution soulève une pléïade de problèmes, de domaines, de type d'information, de moyens algorithmiques très différents qui obligent à briser cette unité au profit d'une division des problèmes. Ainsi, les techniques employées pour résoudre les différents problèmes évoqués précédemment pourront plus rigoureusement trouver leur place dans le cours des traitements.
La division du problème, aussi souhaitable qu'arbitraire, est souvent évoquée dans la littérature. Bien que le nombre de sous problèmes évoqués ne soit jamais le même, la réalité qu'il recouvre est souvent semblable. Nous introduirons ici une division en trois points :détection, reconnaissance et suivi. (cf. figure )
 
   

Figure: La division classique du processus

 

Le premier point à aborder est que cette division en sous-problèmes amène un élément de réponses quant à la structuration de l'information. La représentation de l'information est un problème en soi, et est hautement contraint par l'utilisation d'algorithmes particuliers. Du fait que les traitements à effectuer sont d'ordre très divers, les niveaux de représentations de l'information le sont aussi. On trouve en premier lieu l'image couleur ou monochrome puisque c'est le point de départ du problème, mais aussi des images binaires, les contours, les régions et d'autres objets plus ou moins abstraits. Il est alors important de définir le niveau de structuration de l'information qui prime dans un sous problème particulier. En fait, le traitement de séquence d'images pour la représentation de scène se caractérise souvent par un double processus. Plus l'on abstrait l'information au cours des traitements, tentant de rendre compréhensible son contenu, plus la taille de ses données diminue. L'information croit en contenu informatif en même temps que décroît la taille de ses données.
Compte tenu de la division du problème envisagé la suite sera divisée en trois points correspondants aux trois sous problèmes: détection, reconnaissance et suivi.

La détection

La première étape du traitement de séquence d'images est la détection de mouvement témoignant de l'existence possible de régions mobiles dans l'image courante. Ces indicateurs fournissent alors la base des traitements algorithmiques futurs. On trouve dans la littérature trois familles de méthodes caractérisées par la nature de l'indicateur qu'elles extraient : l'approche basée sur les vitesses, l'approche basée sur l'extraction de primitives et une approche basée l'extraction de régions qualifiées 'd'intérêt'. La suite décrit ces trois familles de méthodes de détection de régions mobiles.

L'approche vitesse

On cherche dans cette approche à qualifier les vitesses dans la scène. Une approche, basée sur l'utilisation des champs de vitesses, est développée dans [Bouthemy, 1988]. Son idée repose sur l'hypothèse d'invariance entre t et t+dt. i.e. la fonction d'intensité lumineuse en un point (x, y, t) est identique en (x+dx, y+dy, t+dt). On definit alors une fonction erreur appelée DFD <<Deplaced Frames Difference>> (1) par:

$\bullet$

(1) DFD(x, y, t) = f(x, y, t)-f(x+dx, y+dy, t+dt)

$\bullet$

(2) $DFD(x, y, t) = 0\ \forall x\ \forall y\ \forall t$

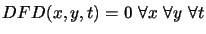
On cherche alors à minimiser la DFD pour tout point (x, y) de l'image à l'instant t donné, pour obtenir une représentation des vitesses 3D projetées dans le plan image. L'équation ainsi obtenue (2) est connue sous le nom de <<Équation de Contrainte du Mouvement Apparent (ECMA)>>. On peut reprocher à cette méthode, outre la lourde phase d'optimisation de la DFD en chaque point de l'image, la mise en oeuvre du procédé.

On trouve aussi dans cette famille la méthode par estimation du flot optique en fonction des variations spatio-temporelles de la fonction d'intensité lumineuse.

  
L'approche région

L'approche région se caractérise par l'extraction dans l'image courante de régions appelées <<blob>>. Ces régions, définies par un ensemble de pixels connexes, correspondent dans l'image à des zones d'intérêt au regard du critère indicateur, en l'occurence les pixels ayant une valeur différente entre un instant et un autre. L'ensemble de ces méthodes peuvent être formalisées ainsi:

$\bullet$

I_resultat = Combi(I₀,...,I_t) (cf. figure )

   

Figure: Combinaison d'images

 

où I_resultat est l'image résultante I₀,...,I_t l'ensemble des images précédentes, Comb est une combinaison de fonctions parmi : Différence, Abs(valeur absolue), Min, Max, Et(et logique), Ou(ou logique)...
L'instance la plus utilisée [] [] de cette classe proposé par [Wenstop, 1983] est la méthode utilisant une différence entre l'image courante et une image de référence, souvent I₀.

$\bullet$

I_resultat = Abs(Diff(I₀, I_t)) (cf. figure )

   

Figure: Combinaison d'images par image de référence

 

On concède à cette méthode sa simplicité de mise en oeuvre.
L'inconvénient majeur et le problème difficile de cette méthode est la mise a jour de l'image de référence.

L'autre instance très utilisée de la classe de méthode de combinaison d'images est la différence d'images successives [Jain et al., 1979]:

$\bullet$

I_resultat = Max(Abs(Diff(I_t, I_t-1)), Abs(Diff(I_t+1, I_t))) (cf. figure )

   

Figure: Combinaison d'images par différence d'images successives et Max

 

Ces méthodes sont souvent utilisées dans les cas d'applications ne pouvant pas se baser sur une image de référence. Cette méthode est, de la même façon, simple à mettre en oeuvre, mais comporte des inconvénients supplémentaires. En effet, cette méthode ne prend pas en compte les changements et mouvements des régions uniformément colorées, seules les régions texturées sont détectées. [Ricquebourg, 1993]

Dans [] l'opérateur Max est remplacé par un <<et>> logique Et. Cette méthode permet de recueillir un résultat proche des résultat de la détection de contours sans avoir recours au calcul du gradient d'intensité de l'image.

$\bullet$

I_resultat = Et(Abs(Diff(I_t, I_t-1)), Abs(Diff(I_t+1, I_t))) (cf. figure )

   

Figure: Combinaison d'images par différence images successives et Et 

 

L'extraction de primitives

Cette approche consiste à recueillir dans l'image courante des points particuliers des objets de la scène. Ces points particuliers sont appelés primitives et sont les arêtes, contours ou autre points caractéristiques. Dans [Du et al., 1993] [Koller et al., 1993] les auteurs s'intéressent à la détection des véhicules, ils utilisent pour cela l'extraction de primitives sur les voitures telles que les angles du toit et du capot. Ces primitives sont obtenues grâce à l'analyse de la norme du gradient de l'image et toute autre méthode permettant l'extraction de contours (filtre de Sobel, seuillage par hysteresis, Canny, suivi de contour, etc ...). Cette famille de méthodes possède comme grand avantage de produire des indicateurs ayant un contenu sémantique (i.e. des points précis d'objets), ce qui est un avantage pour les traitements ultérieurs.

Bilan

Le point commun de toutes ces méthodes est donc l'extraction à chaque image de la séquence d'indicateurs qui témoignent des changements dans l'image. Il faut dès lors prendre garde à l'assimilation abusive entre changement et mouvement. Comme nous le verrons plus tard sous certaines hypothèses les deux notions se confondent, mais il existe aussi des cas de changement n'étant pas causé par du mouvement et réciproquement. L'extraction d'indicateurs de changement est donc une étape importante de l'ensemble des traitements sur la séquence d'images car le reste des traitements est contraint par la nature de ces indicateurs. Les algorithmes applicables aux primitives ne le sont pas forcement aux régions, et réciproquement.

La reconnaissance

Les indices émergeants de la première étape doivent être organisés (filtrage, régularisation, ordonnancement, groupement, etc...). Le but est d'obtenir à la fin de la phase de reconnaissance un ensemble d'objets potentiellement utilisables par les outils traitants les aspects dynamiques. Il s'agit en fait de raffiner, voir établir complètement, la décision sur l'intérêt de zones particulières de l'image. Cette étape pose le problème de ce que l'on cherche à voir dans chacune des images de la séquence. La première difficulté est donc de pouvoir catégoriser ce que l'on veut reconnaître. Le second problème est de savoir comment le reconnaître ( i.e. quelles techniques employer ?). Nous ne développerons pas ce dernier point; on trouve dans la littérature différentes optiques telles que des contraintes sur l'organisation des indicateurs ou l'optimisation d'une fonction décrivant l'ensemble non-ordonné des indices [Du et al., 1993] [Koller et al., 1993]. Pour le premier problème, de la même façon que nous avons procédé à l'analyse du problème de détection du point de vue de la nature des objets détectés, l'analyse du problème de reconnaissance sera faite selon la nature des objets reconnus. Guidé par les contraintes algorithmiques, les objets à reconnaître sont caractérisés par leur potentiel de déformation intrinsèque, leur rigidité. Les objets rigides sont donc les objets dont la forme ne varie pas au cours du temps, seule la projection dans le plan image peut différer. A une rotation, une translation et une homotétie près un objet rigide conserve sa forme propre. En fait, ce sont les paramètres de ces opérations que les méthodes qui utilisent ces objets visent à estimer pour pouvoir instancier un modèle dans l'image courante. A l'opposé, les objets non rigides ne peuvent pas être considérés de forme constante.

Nous organiserons l'étude des différents modèles d'objets rencontrés selon deux axes : les modèles d'apparence d'objets et les modèles d'objets réels.

Les modèles d'apparence d'objets

Cette famille de méthodes basées sur l'apparence des objets est souvent employée dans les cas où il est difficile de qualifier l'objet pour des raisons de bruit trop important ou dans les cas d'objets trop complexes ou trop divers. Dans [Bremond, 1997] l'étape de détection fournit un résultat bruité qui ne permet pas l'instanciation d'un modèle d'objet complexe. Le cadre de travail reste donc dans le plan image et les indices en deux dimensions. Dans [Choi et al., 1997], les auteurs utilisent un modèle d'apparence d'objets. Le champ d'application est l'analyse de scène sportive et notamment de football. Plutôt qu'un contraignant modèle d'objet, les auteurs choisissent une décision basée sur l'analyse des couleurs. Dans [], les auteurs justifient leur approche par l'impossibilité de définir un modèle d'objet pour leur champs d'études. Il n'y a pas de reconnaissance d'objets mais plutôt reconnaissance de zone. [] définit un modèle d'apparence d'objet non rigide complexe pour l'analyse du mouvement humain. Les auteurs définissent un modèle 2D de forme grâce à l'extraction d'un vecteur de points du contour de la projection de l'humain dans le plan image, se basant pour cela sur un modèle de distribution appelés PDM : <<Point Distribution Model>> emprunté au travaux de Cootes. L'idée est de mesurer la différence dx entre un modèle quelconque et le modèle moyen. i.e. dx = x - x_moyen où x est un vecteur de points obtenu et x_moyen est le vecteur moyen. L'analyse des vecteurs dx donne le mode de variation le plus significatif du modèle. La forme du contour est ensuite optimisée par l'utilisation de b-splines cubiques dont les points de contrôle sont chacun des points du contour définis plus haut. Les résultats sont mesurés sur le critère de compacité du modèle. Des résultats intéressants sont obtenus sur un ensemble d'apprentissage réduit à des personnes marchant latéralement. Sur un ensemble d'apprentissage quelconque les résultats sont plus modestes mais encore utilisables (cf.illustration ).
 
   

Figure: Le model d'apparence d'objet non-rigide de Hogg(95)

 

L'avantage de l'utilisation de modèles d'objets basés sur l'apparence est de pouvoir être instanciés très tôt dans les traitements, juste après la détection qui, par définition, recueille des indices d'apparence. Le défaut majeur est de ne pas tenir compte de l'aspect volumique ou de caractéristiques intrinsèques de l'objet.

Les modèles d'objets réels

Les modèles d'objets réels utilisent quant à eux des caractéristiques de l'objet. Les méthodes basées sur l'utilisation de modèle d'objets réels exploitent souvent des propriétés plus naturelles. A titre d'exemple les objets rigides, comme les véhicules, peuvent être simplement décris, sur des considérations volumiques. Dans [Koller et al., 1993], l'objet consiste en un polyèdre 3D modélisant un véhicule par douze degrés de liberté. L'ensemble de segments de contours obtenus par l'étape de détection est alors mis en correspondance avec les arêtes du modèle polyèdrique par un processus itératif emprunté aux travaux de [Lowe, 1987]. L'idée est de minimiser un critère, défini par une mesure de distance (distance de Mahalanobis), pour chaque arête du polyèdre (cf.illustration ).
 
   

Figure: Le modèle d'objet réel rigide de Koller(93)

 

Les modèles objets non rigides sont tous les objets dont la forme propre n'est pas constante au cours du temps (on entend par là: à une rotation, translation et homotétie près). C'est le cas de la plupart des objets naturels: végétaux, animaux, humains. Le traitement de tels objets requiert l'utilisation de modèles et de techniques particulièrs. Mais le problème lié aux personnes est double et peut être défini ainsi. D'une part, soit une personne donnée, les caractéristiques la décrivant ne sont pas constantes au cours du temps. En effet il existe une forte variation de formes pendant les déplacements (oscillations des bras et des jambes), voire même une variation de couleur. D'autre part, soient deux personnes données, les caractéristiques les décrivant ne sont pas forcément les même. Ce second point pose un problème quant à la généralité du modèle.

Dans [Atika, 1984], l'auteur utilise un modèle de personne défini par un squelette de six segments (deux bras, deux jambes, torse et tête).

Dans [] un modèle de squelette de dix-sept segments est utilisé. Un modèle volumique constitué de quatorze cylindres elliptiques est utilisé dans [Rohr, 1994].

L'avantage de ces modèles d'objets réel est d'aller dans le sens d'une indépendance entre les contraintes du modèle et les algorithmes de reconnaissance. Ceci permet de garder un contrôle sur l'instanciation que ne permet pas les méthode à base de modèle d'apparence d'objets. L'inconvénient est d'éloigner la reconnaissance de l'objet de l'extraction d'indices de mouvement; de nombreuses étapes sont nécessaire pour instancier un modèle d'objet réel par un ensemble de détections.

Bilan

L'organisation des indices émergeant de la détection en objets potentiellement utilisables est un problème, basiquement complexe, rendu encore plus difficile par l'introduction de modèles d'objets. Néanmoins, plus l'on cherche une qualification précise du contenu de la scène, plus l'utilisation de connaissances a priori devient cruciale. Comme nous l'avons vu, l'emploi de modèles d'objets permet d'établir, lors de la reconnaissance, la décision sur l'existence ou non d'objet particulier dans la scène. Ce point est primordial dans la mesure où les traitements des étapes suivantes (le suivi en particulier) seront conditionnés par la qualité de la reconnaissance.

L'appariement temporel et le suivi

Contrairement aux étapes précédentes dont les traitements pouvaient être qualifiés de statique dans le sens où ils avaient pour objet l'analyse d'une seule et unique image, les méthodes qui seront exposées dans la suite ont une dimension supplémentaire à traiter : le temps. Le but des traitements de cette étape est d'inclure les résultats de la détection et de la reconnaissance dans la continuité de la séquence d'images. Pour cela plusieurs techniques sont abordées. Le point discriminant ces méthodes est l'usage fait des mesures courantes (les mesures faite sur l'image courante). Une première famille de méthodes vise à mettre en correspondance ces mesures avec celles obtenues précédemment, à l'opposé d'autres techniques utilisent ces mesures pour vérifier la cohérence d'une prédiction faite grâce à l'ensemble des résultats des images précédentes. La suite est divisée en deux points correspondants à ces deux paradigmes.

La mise en correspondance

La première famille de méthodes évoquées par [] est la mise en correspondance directe. On cherche ici à placer les mesures reçues des étapes précédentes dans la continuité des mesures réalisées sur les images précédentes. Formellement, il s'agit de prolonger la suite des détections par les détections obtenues à l'image courante en minimisant l'erreur commise par cet appariement. Nous détaillerons plus précisément cette approche dans la troisième partie puisque c'est l'orientation prise.

Le filtre de Kalman

L'autre famille très populaire de résolution de problème de suivi est l'estimation par filtre de Kalman. La philosophie générale du procédé s'oppose à la précédente approche par l'utilisation des mesures courantes. Dans ce cas le traitement se fait en deux temps. Premièrement, on génère une prédiction de ce que pourrait être le résultat courant à partir de l'ensemble des résultats précédents, puis l'on compare le résultat prédit avec les mesures réellement obtenues. Les données des étapes ultérieures ont alors un rôle de vérification. Plus précisément, le filtrage de Kalman utilisé par [] et [Choi et al., 1997] et [Ricquebourg, 1997] se définit comme un filtre récursif produisant une prédiction de l'état courant E_t du système à partir de l'ensemble des mesures M_t-k, . .., M_t-1 si l'évolution dynamique du système est considéré comme linéaire.

$\bullet$

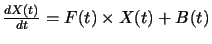$\frac{\large dX(t) }{\large dt} \normalsize = F(t) \timesX(t) + B(t)$ où

F(t) représente l'évolution du système.
X(t) est un vecteur d'état.
B(t) un terme tenant compte du bruit et des termes non-homogènes souvent nuls.

La résolution de cette équation puis un passage en mesure discrète donne X(t) en fonction de X(t-1) et un terme correspondant à l'évolution dynamique du système. Ce qui permet de calculer, avec une précision dépendant du modèle de mouvement considéré, l'état du système à l'instant t.

L'intérêt est double; obtenir une prédiction à l'étape courante indépendante des mesures réalisées et mesurer la fiabilité du modèle de mouvement grâce aux mesures obtenues. L'inconvénient, outre la délicate mise en oeuvre du procédé, est aussi double. D'une part, l'utilisation du filtre de Kalman nécessite une modélisation de l'évolution dynamique des objets de la scène (ce qui n'est pas trivial puisqu'elle est associée au mouvement humain), d'autre part, comme tout processus itératif sa sensibilité aux valeurs initiales est grande.

Bilan

Une fois encore, l'apport de modèle (de mouvement, cette fois) permet d'augmenter la robustesse des traitements. Toute fois, autant l'intégration d'un modèle d'objet en reconnaissance était concevable, autant l'élaboration d'un modèle de mouvement global d'une scène parait plus délicat.

Les conclusions

La division des problèmes introduite dans cette section comprend donc trois points que sont la détection, la reconnaissance et le suivi, chacun ayant des hypothèses, des outils algorithmiques, des domaines très différents. Le but de cette division nous l'avons vu est double. D'une part, ceci nous permet de reprendre un par un les problèmes évoqués dans la première section et d'insérer dans le fil des traitements les algorithmes permettant de les résoudre. D'autre part, cette division des problèmes permet de comprendre l'importance d'introduire des modélisations des objets et des mouvements afin d'augmenter la robustesse des traitements de chacun des sous problèmes.

1998-09-22