Manipulateurs à degrés de liberté complexes/Robots with complex DOF

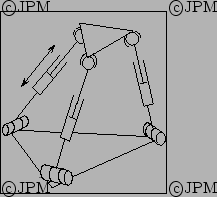
$\begin{figure}\begin{center} \ifx\cs\tempdima \newdimen \tempdima\fi \ifx\cs\tem... ...wx}} \end{picture} \setlength{\unitlength}{1cm} \par \end{center} \end{figure}$

Le manipulateur à 3 degrés de liberté de Lee. Les articulations des segments avec la base sont , disposées à 120 degrés. Les articulations avec le plateau mobile sont des rotules et des actionneurs prismatiques permettent de faire varier la longueur des segments. Les degrés de liberté sont des translations sur l'axe vertical et les angles de précession et de nutation, d'après Lee [102].
Lee mechanism: a link of this mechanism is constituted (from the base to the platform) by a passive revolute joint, an actuated prismatic joint and a ball-and-socket joint.

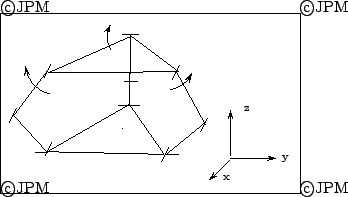
$\begin{figure}\begin{center} \ifx\cs\tempdima \newdimen \tempdima\fi \ifx\cs\tem... ...){z} \end{picture} \setlength{\unitlength}{1cm} \par \end{center} \end{figure}$

Une variante du mécanisme de Lee, le robot HALF [109,110]. Les actionneurs prismatiques sont remplacés par des actionneurs rotatifs. Les mouvements possibles sont la rotation autour de y et les translation en y,z.

A variant of Lee mechanism: the linear actuator are substituted by rotary one and a specific geometry allow to have rotation around the y axis and translation along the y, z axis

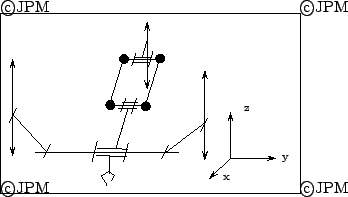
$\begin{figure}\begin{center} \ifx\cs\tempdima \newdimen \tempdima\fi \ifx\cs\tem... ...){z} \end{picture} \setlength{\unitlength}{1cm} \par \end{center} \end{figure}$

Une autre variante du HALF [111]. Les actionneurs sont prismatiques et les mouvements possibles sont la rotation autour de y et les translation en y,z.

A variant of the HALF robot: the actuators are linear and a specific geometry allow to have rotation around the y axis and translation along the y, z axis

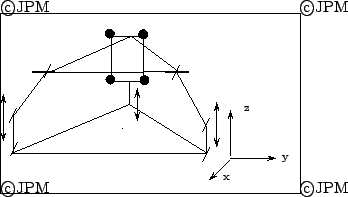
$\begin{figure}\begin{center} \ifx\cs\tempdima \newdimen \tempdima\fi \ifx\cs\tem... ...){z} \end{picture} \setlength{\unitlength}{1cm} \par \end{center} \end{figure}$

Une autre variante du mécanisme de Lee où les actionneurs rotatifs sont remplacés par des prismatiques[2]. Les mouvements possibles sont la rotation autour de y et les translation en y,z.

A variant of Lee mechanism: the revolute actuator are substituted by linear one and a specific geometry allow to have rotation around the y axis and translation along the y, z axis

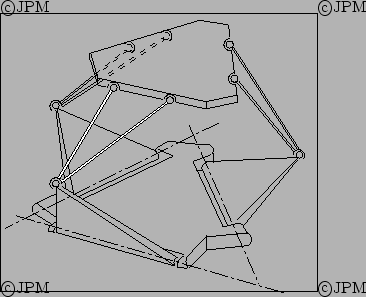
$\begin{figure}\begin{center} \ifx\cs\tempdima \newdimen \tempdima\fi \ifx\cs\tem... ...wx}} \end{picture} \setlength{\unitlength}{1cm} \par \end{center} \end{figure}$

Une structure proposée par Lambert. Les triangles articulés proches de la base sont motorisés, d'après Lambert [96].
A structure proposed by Lambert: the revolute joints connected to the base are actuated.

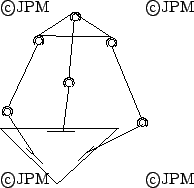
$\begin{figure}\begin{center} \ifx\cs\tempdima \newdimen \tempdima\fi \ifx\cs\tem... ...wx}} \end{picture} \setlength{\unitlength}{1cm} \par \end{center} \end{figure}$

L'équivalent de Dunlop où les articulations proches de la base sont motorisés, d'après Dunlop [37].
A mechanism equivalent to the previous mechanism.

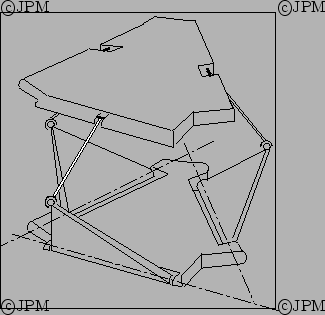
$\begin{figure}\begin{center} \ifx\cs\tempdima \newdimen \tempdima\fi \ifx\cs\tem... ...wx}} \end{picture} \setlength{\unitlength}{1cm} \par \end{center} \end{figure}$

(d'après [73]).

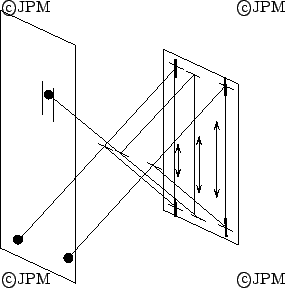
$\begin{figure}\begin{center} \ifx\cs\tempdima \newdimen \tempdima\fi \ifx\cs\tem... ...wx}} \end{picture} \setlength{\unitlength}{1cm} \par \end{center} \end{figure}$

Le mécanisme de Chung à base de 4 barres qui permet d'avoir un degré de liberté en translation et 2 en rotation (d'après [28]).

A four-bar based robot, allowing one translational dof and two rotations

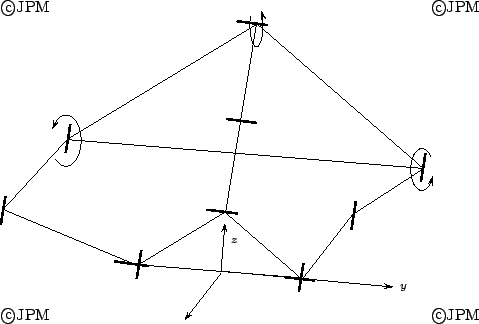
$\begin{figure}\begin{center} \ifx\cs\tempdima \newdimen \tempdima\fi \ifx\cs\tem... ...$z$} \end{picture} \setlength{\unitlength}{1cm} \par \end{center} \end{figure}$

Une variante qui permet d'avoir un mouvement cylindrique: rotation autour de y, translation selon y, z (d'après [174])

An equivalent that allow to have cylindrical motion: rotation around y, translation along y,z

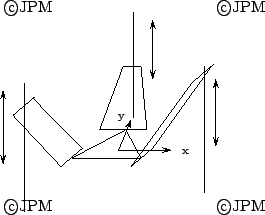
$\begin{figure}\begin{center} \ifx\cs\tempdima \newdimen \tempdima\fi \ifx\cs\tem... ...){y} \end{picture} \setlength{\unitlength}{1cm} \par \end{center} \end{figure}$

Une variante qui permet d'avoir un mouvement cylindrique: rotation autour de y, translation selon y, z (d'après [118,79]), utilisé par Fatronik pour la machine-outil VERNE

An equivalent that allow to have cylindrical motion: rotation around y, translation along y,z, used in the VERNE machine-tool

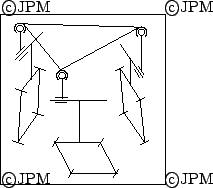
$\begin{figure}\begin{center} \ifx\cs\tempdima \newdimen \tempdima\fi \ifx\cs\tem... ...wx}} \end{picture} \setlength{\unitlength}{1cm} \par \end{center} \end{figure}$

Le mécanisme de Ceccarelli: les mécanismes à 4 barres sont actionnés et modifie la position d'une articulation prismatique qui est liée au plateau mobile par une rotule (d'après [24]).
Ceccarelli mechanism: the four-bars mechanism are actuated and are used to modify the position of a passive prismatic joint which is connected to the moving platform by a ball-and-socket joint.

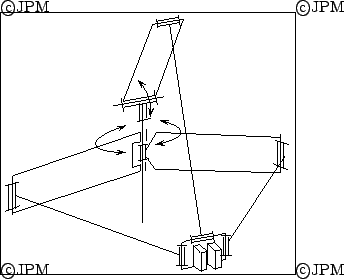
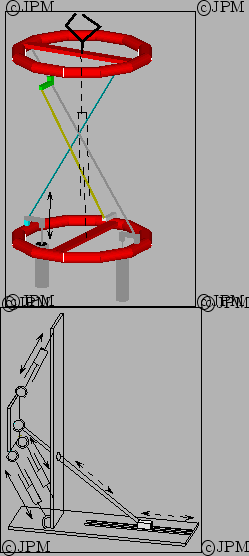
$\begin{figure}\begin{center} \ifx\cs\tempdima \newdimen \tempdima\fi \ifx\cs\tem... ...wx}} \end{picture} \setlength{\unitlength}{1cm} \par \end{center} \end{figure}$

Le robot cylindrique de Reboulet [147]. A cylindrical robot suggested by Reboulet [147].

$\begin{figure}\begin{center} \ifx\cs\tempdima \newdimen \tempdima\fi \ifx\cs\tem... ...wx}} \end{picture} \setlength{\unitlength}{1cm} \par \end{center} \end{figure}$

Robots à 3 degrés de liberté avec des contraintes passives. En haut et au milieu les vérins assurent un déplacement des points d'articulation. La rotation autour de la normale au plateau mobile est obtenue par une tige articulée avec des cardans, libre selon son axe, d'après Lande [97].

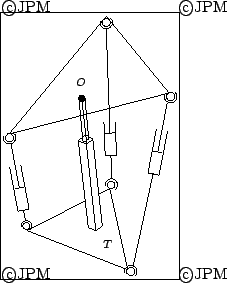
$\begin{figure}\begin{center} \ifx\cs\tempdima \newdimen \tempdima\fi \ifx\cs\tem... ...$T$} \end{picture} \setlength{\unitlength}{1cm} \par \end{center} \end{figure}$

Une architecture proposée par Reboulet. La barre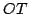

, reliée à la base par un cardan en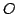

, est extensible mais ne peut tourner autour de son axe, d'après Reboulet [144].

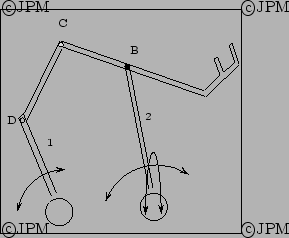
$\begin{figure}\begin{center} \ifx\cs\tempdima \newdimen \tempdima\fi \ifx\cs\tem... ...){B} \end{picture} \setlength{\unitlength}{1cm} \par \end{center} \end{figure}$

Le robot à 3 degrés de liberté de Stoughton, d'après Stoughton [164].

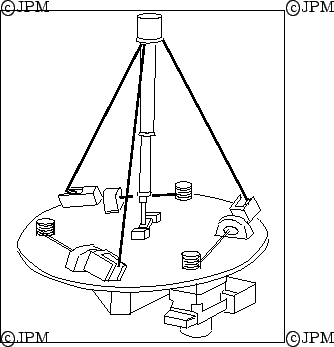
$\begin{figure}\begin{center} \ifx\cs\tempdima \newdimen \tempdima\fi \ifx\cs\tem... ...wx}} \end{picture} \setlength{\unitlength}{1cm} \par \end{center} \end{figure}$

Le robot à 3 degrés de liberté de Landsberger: les segments sont des câbles qui peuvent s'enrouler sur des tambours. La tension des câbles est assurée par le mât central qui exerce une poussée passive vers le haut, d'après Landsberger [98].

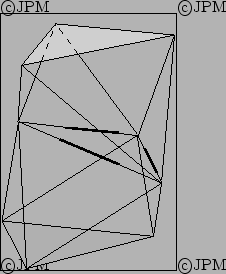
$\begin{figure}\begin{center} \ifx\cs\tempdima \newdimen \tempdima\fi \ifx\cs\tem... ...wx}} \end{picture} \setlength{\unitlength}{1cm} \par \end{center} \end{figure}$

Le robot de Arun. permettent de modifier les longueurs des côtés de la face triangulaire commune aux deux octaèdres, d'après Arun [8].

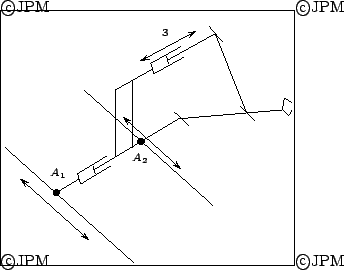
$\begin{figure}\begin{center} \ifx\cs\tempdima \newdimen \tempdima\fi \ifx\cs\tem... ...){3} \end{picture} \setlength{\unitlength}{1cm} \par \end{center} \end{figure}$

Le mécanisme de translation de Cheng. Les translations des points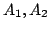

permettent de placer l'organe terminal dans une position quelconque dans un plan alors que l'actionneur 3 permet de changer son élévation (d'après [27])
Cheng mechanism: the translation of points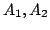

enable to put the end-effector center anywhere in a plane while actuator 3 enable to change its elevation

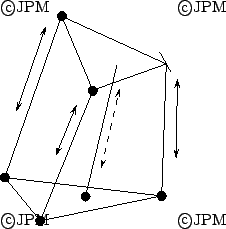
$\begin{figure}\begin{center} \ifx\cs\tempdima \newdimen \tempdima\fi \ifx\cs\tem... ...wx}} \end{picture} \setlength{\unitlength}{1cm} \par \end{center} \end{figure}$

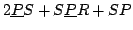Le $2\underline{P}S+S\underline{P}R+SP$ de Lu [113]. La jambe centrale et l'articulation

imposent que les degrés de liberté soient une translation selon l'axe de la jambe et deux orientations.

The central passive leg and the

joint impose that the end-effector platform d.o.f. are a translation along the leg and two orientations.

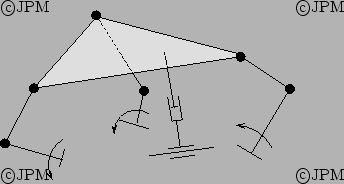
$\begin{figure}\begin{center} \ifx\cs\tempdima \newdimen \tempdima\fi \ifx\cs\tem... ...wx}} \end{picture} \setlength{\unitlength}{1cm} \par \end{center} \end{figure}$

Une variante: le robot 3- $\underline{R}$ SS+CP de Hess-Coelho [68]. Le mât central est articulé sur une articulation passive cylindrique et posséde une articulation prismatique passive.

A variant: the 3-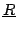 $\underline{R}$ SS+CP. The central mast is connected to the base by a passive cylindrical joint and has a passive prismatic joint.

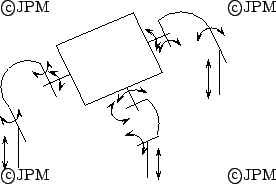
$\begin{figure}\begin{center} \ifx\cs\tempdima \newdimen \tempdima\fi \ifx\cs\tem... ...wx}} \end{picture} \setlength{\unitlength}{1cm} \par \end{center} \end{figure}$

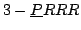Une robot de type $3-\underline{P}RRR$ , avec 3 degrés de liberté: une translation et deux rotations [148].

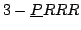A $3-\underline{P}RRR$ robot with 3 degrees of freedom: one translation and two rotations

$\begin{figure}\begin{center} \ifx\cs\tempdima \newdimen \tempdima\fi \ifx\cs\tem... ...wx}} \end{picture} \setlength{\unitlength}{1cm} \par \end{center} \end{figure}$

Une robot avec 3 degrés de liberté: deux translations et une rotation [187].

A robot with 3 degrees of freedom: two translations and one rotation

Next: Manipulateurs à degrés de liberté variables/Manipulator with variable d.o.f. Up: Manipulateurs à 3 degrés de liberté/3 DOF robots Previous: Manipulateurs pour orientation/Orientation robots