|
Classes |
| class | edge_num |
| | An edge numbering class. More...
|
| class | spvecgf2 |
| | A sparse vector with elements in GF2. More...
|
| class | spvecfp |
| | A sparse vector with elements in  . More... . More...
|
Undirected Minimum Cycle Basis |
These functions implement the three main approaches for computing a minimum cycle basis. All these approaches are based on the Support Vector Approach. Their differences are on the way of finding the shortest non-orthogonal cycle:
- mcb::UMCB_SVA finds the cycles by maintaining a signed graph
- mcb::UMCB_HYBRID maintains a list of candidate cycles which is guarantied to contain an MCB,
- mcb::UMCB_FH maintains the same list as above but in a more elaborate way in order to be able to compute faster the shortest non-orthogonal cycle.
In case you have no special preference try the mcb::UMCB function which uses the signed graph implementation and supports multigraphs.
The fastest algorithm is mcb::UMCB_SVA.
|
| template<class Container> |
| int | UMCB_SVA (const graph &g, array< Container > &mcb, array< Container > &proof, const mcb::edge_num &enumb) |
| | Compute a MCB of an undirected graph using the Support Vector Approach (de Pina's PhD thesis) algorithm.
|
| template<class Container> |
| int | UMCB_SVA (const graph &g, array< Container > &mcb, const mcb::edge_num &enumb) |
| | Compute a MCB of an undirected weighted graph using the Support Vector Approach (de Pina's PhD thesis) algorithm.
|
| template<class W, class Container> |
| W | UMCB_SVA (const graph &g, const edge_array< W > &len, array< Container > &mcb, array< Container > &proof, const mcb::edge_num &enumb) |
| | Compute a MCB of an undirected weighted graph using the Support Vector Approach (de Pina's PhD thesis) algorithm.
|
| template<class W, class Container> |
| W | UMCB_SVA (const graph &g, const edge_array< W > &len, array< Container > &mcb, const mcb::edge_num &enumb) |
| | Compute a MCB of an undirected weighted graph using the Support Vector Approach (de Pina's PhD thesis) algorithm.
|
| int | UMCB_HYBRID (const leda::graph &g, leda::array< leda::d_int_set > &mcb, leda::array< leda::d_int_set > &proof, const mcb::edge_num &enumb) |
| | Compute a minimum cycle basis of an undirected graph using a hybrid algorithm.
|
| int | UMCB_HYBRID (const leda::graph &g, leda::array< leda::d_int_set > &mcb, const mcb::edge_num &enumb) |
| | Compute a minimum cycle basis of an undirected graph using a hybrid algorithm.
|
| template<class W> |
| W | UMCB_HYBRID (const graph &g, const edge_array< W > &len, array< d_int_set > &mcb, array< d_int_set > &proof, const mcb::edge_num &enumb) |
| | Compute a minimum cycle basis of a weighted undirected graph using a hybrid algorithm.
|
| template<class W> |
| W | UMCB_HYBRID (const graph &g, const edge_array< W > &len, array< d_int_set > &mcb, const mcb::edge_num &enumb) |
| | Compute a minimum cycle basis of a weighted undirected graph using a hybrid algorithm.
|
| template<class W> |
| W | UMCB_FH (const graph &g, const edge_array< W > &len, array< mcb::spvecgf2 > &mcb, array< mcb::spvecgf2 > &proof, const mcb::edge_num &enumb) |
| | Compute a MCB of an undirected weighted graph using a Fast variant of the Hybrid algorithm.
|
| template<class W> |
| W | UMCB_FH (const graph &g, const edge_array< W > &len, array< mcb::spvecgf2 > &mcb, const mcb::edge_num &enumb) |
| | Compute a MCB of an undirected weighted graph using a Fast variant of the Hybrid algorithm.
|
Directed Minimum Cycle Basis |
| template<class W> |
| W | DMCB (const graph &g, const edge_array< W > &len, array< mcb::spvecfp > &mcb, array< mcb::spvecfp > &proof, const mcb::edge_num &enumb, double error=0.375) |
| | Compute a minimum cycle basis of a weighted directed graph.
|
| template<class W> |
| W | DMCB (const graph &g, const edge_array< W > &len, array< mcb::spvecfp > &mcb, const mcb::edge_num &enumb, double error=0.375) |
| | Compute a minimum cycle basis of a weighted directed graph.
|
| template<class W> |
| W | DMCB (const graph &g, const edge_array< W > &len, array< array< etype > > &mcb, const mcb::edge_num &enumb, double error=0.375) |
| | Compute a minimum cycle basis of a weighted directed graph.
|
Undirected Approximate Minimum Cycle Basis |
| template<class W> |
| W | UMCB_APPROX (const graph &g, const edge_array< W > &len, const int k, array< mcb::spvecgf2 > &mcb, const mcb::edge_num &enumb) |
| | Compute an undirected approximate MCB of a weighted graph.
|
| int | UMCB_APPROX (const graph &g, const int k, array< mcb::spvecgf2 > &mcb, const mcb::edge_num &enumb) |
| | Compute an undirected approximate MCB of a graph.
|
Directed Approximate Minimum Cycle Basis |
| template<class W> |
| W | DMCB_APPROX (const graph &g, const edge_array< W > &len, const int k, array< mcb::spvecfp > &mcb, const mcb::edge_num &enumb, double error=0.375) |
| | Compute a directed approximate MCB of a weighted graph.
|
| template<class W> |
| W | DMCB_APPROX (const graph &g, const edge_array< W > &len, const int k, array< mcb::spvecfp > &mcb, const mcb::edge_num &enumb, mcb::ptype prime) |
| | Compute a directed approximate MCB of a weighted graph in 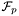 . Note that the minimum cycle basis in . Note that the minimum cycle basis in 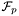 might not be the minimum cycle basis of the graph. might not be the minimum cycle basis of the graph.
|
Undirected Minimum Cycle Basis |
The functions below are the more general implementation for undirected graphs. They also support multigraphs. As an underlying implementation they use the Support Vector approach (mcb::UMCB_SVA). They should be the first choice of use unless some special requirements exist.
|
| template<class W> |
| W | UMCB (const graph &g, const edge_array< W > &len, array< mcb::spvecgf2 > &mcb, const mcb::edge_num &enumb) |
| | Compute an MCB of an undirected graph (possible a multigraph) using the most general implementation of this library.
|
| int | UMCB (const graph &g, array< mcb::spvecgf2 > &mcb, const mcb::edge_num &enumb) |
| | Compute an MCB of an undirected graph (possible a multigraph) using the most general implementation of this library.
|
| template<class Container> |
| void | cycle_matrix (const graph &g, const array< Container > &cb, const mcb::edge_num &enumb, integer_matrix &B) |
| | Compute the cycle matrix of a cycle basis.
|
| std::ostream & | output_maple_format (std::ostream &out, const integer_matrix &B) |
| | Output a LEDA integer_matrix in a format compatible with maple.
|
| template<class Container> |
| leda::integer | determinant (const graph &g, const array< Container > &cb, const mcb::edge_num &enumb) |
| | Compute the determinant of a cycle basis.
|
Typedefs |
| typedef int | indextype |
| typedef leda::integer | ptype |
Functions |
| std::ostream & | operator<< (std::ostream &o, const spvecgf2 &v) |
| std::istream & | operator>> (std::istream &o, spvecgf2 &v) |
| std::ostream & | operator<< (std::ostream &o, const spvecfp &v) |
 . More...
. More...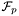 . Note that the minimum cycle basis in
. Note that the minimum cycle basis in 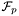 might not be the minimum cycle basis of the graph.
might not be the minimum cycle basis of the graph.  1.4.6
1.4.6