Undirected Approximate Minimum Cycle Basis
Directed Approximate Minimum Cycle Basis
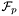 . Note that the minimum cycle basis in
. Note that the minimum cycle basis in 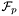 might not be the minimum cycle basis of the graph.
might not be the minimum cycle basis of the graph.
Undirected Approximate Minimum Cycle Basis | |
| template<class W> | |
| W | mcb::UMCB_APPROX (const graph &g, const edge_array< W > &len, const int k, array< mcb::spvecgf2 > &mcb, const mcb::edge_num &enumb) |
| Compute an undirected approximate MCB of a weighted graph. | |
| int | mcb::UMCB_APPROX (const graph &g, const int k, array< mcb::spvecgf2 > &mcb, const mcb::edge_num &enumb) |
| Compute an undirected approximate MCB of a graph. | |
Directed Approximate Minimum Cycle Basis | |
| template<class W> | |
| W | mcb::DMCB_APPROX (const graph &g, const edge_array< W > &len, const int k, array< mcb::spvecfp > &mcb, const mcb::edge_num &enumb, double error=0.375) |
| Compute a directed approximate MCB of a weighted graph. | |
| template<class W> | |
| W | mcb::DMCB_APPROX (const graph &g, const edge_array< W > &len, const int k, array< mcb::spvecfp > &mcb, const mcb::edge_num &enumb, mcb::ptype prime) |
Compute a directed approximate MCB of a weighted graph in 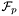 . Note that the minimum cycle basis in . Note that the minimum cycle basis in 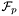 might not be the minimum cycle basis of the graph. might not be the minimum cycle basis of the graph. | |
|
||||||||||||||||||||||||||||||||
|
Compute a directed approximate MCB of a weighted graph in
The basis is returned as an array of sparse vectors, spvecfp, called mcb.
The function returns the weight of the possibly approximate Minimum Cycle Basis or is undefined if there were any errors.
The running time is
|
|
||||||||||||||||||||||||||||||||
|
Compute a directed approximate MCB of a weighted graph.
The function computes an
Since the algorithm is a randomized Monte-Carlo algorithm, the error argument which should be less that 1 represents the acceptable error probability that the returned cycle basis is not a
The function returns the weight of the approximate Minimum Cycle Basis or is undefined if there were any errors.
The running time is
|
|
||||||||||||||||||||
|
Compute an undirected approximate MCB of a graph.
The function computes an
The function returns the weight of the approximate Minimum Cycle Basis or is undefined if there were any errors.
The running time is
|
|
||||||||||||||||||||||||||||
|
Compute an undirected approximate MCB of a weighted graph.
The function computes an
The function returns the weight of the approximate Minimum Cycle Basis or is undefined if there were any errors.
The running time is
|
 1.4.6
1.4.6