|
Undirected Minimum Cycle Basis |
These functions implement the three main approaches for computing a minimum cycle basis. All these approaches are based on the Support Vector Approach. Their differences are on the way of finding the shortest non-orthogonal cycle:
- mcb::UMCB_SVA finds the cycles by maintaining a signed graph
- mcb::UMCB_HYBRID maintains a list of candidate cycles which is guarantied to contain an MCB,
- mcb::UMCB_FH maintains the same list as above but in a more elaborate way in order to be able to compute faster the shortest non-orthogonal cycle.
In case you have no special preference try the mcb::UMCB function which uses the signed graph implementation and supports multigraphs.
The fastest algorithm is mcb::UMCB_SVA.
|
| template<class Container> |
| int | mcb::UMCB_SVA (const graph &g, array< Container > &mcb, array< Container > &proof, const mcb::edge_num &enumb) |
| | Compute a MCB of an undirected graph using the Support Vector Approach (de Pina's PhD thesis) algorithm.
|
| template<class Container> |
| int | mcb::UMCB_SVA (const graph &g, array< Container > &mcb, const mcb::edge_num &enumb) |
| | Compute a MCB of an undirected weighted graph using the Support Vector Approach (de Pina's PhD thesis) algorithm.
|
| template<class W, class Container> |
| W | mcb::UMCB_SVA (const graph &g, const edge_array< W > &len, array< Container > &mcb, array< Container > &proof, const mcb::edge_num &enumb) |
| | Compute a MCB of an undirected weighted graph using the Support Vector Approach (de Pina's PhD thesis) algorithm.
|
| template<class W, class Container> |
| W | mcb::UMCB_SVA (const graph &g, const edge_array< W > &len, array< Container > &mcb, const mcb::edge_num &enumb) |
| | Compute a MCB of an undirected weighted graph using the Support Vector Approach (de Pina's PhD thesis) algorithm.
|
| int | mcb::UMCB_HYBRID (const leda::graph &g, leda::array< leda::d_int_set > &mcb, leda::array< leda::d_int_set > &proof, const mcb::edge_num &enumb) |
| | Compute a minimum cycle basis of an undirected graph using a hybrid algorithm.
|
| int | mcb::UMCB_HYBRID (const leda::graph &g, leda::array< leda::d_int_set > &mcb, const mcb::edge_num &enumb) |
| | Compute a minimum cycle basis of an undirected graph using a hybrid algorithm.
|
| template<class W> |
| W | mcb::UMCB_HYBRID (const graph &g, const edge_array< W > &len, array< d_int_set > &mcb, array< d_int_set > &proof, const mcb::edge_num &enumb) |
| | Compute a minimum cycle basis of a weighted undirected graph using a hybrid algorithm.
|
| template<class W> |
| W | mcb::UMCB_HYBRID (const graph &g, const edge_array< W > &len, array< d_int_set > &mcb, const mcb::edge_num &enumb) |
| | Compute a minimum cycle basis of a weighted undirected graph using a hybrid algorithm.
|
| template<class W> |
| W | mcb::UMCB_FH (const graph &g, const edge_array< W > &len, array< mcb::spvecgf2 > &mcb, array< mcb::spvecgf2 > &proof, const mcb::edge_num &enumb) |
| | Compute a MCB of an undirected weighted graph using a Fast variant of the Hybrid algorithm.
|
| template<class W> |
| W | mcb::UMCB_FH (const graph &g, const edge_array< W > &len, array< mcb::spvecgf2 > &mcb, const mcb::edge_num &enumb) |
| | Compute a MCB of an undirected weighted graph using a Fast variant of the Hybrid algorithm.
|
Directed Minimum Cycle Basis |
| template<class W> |
| W | mcb::DMCB (const graph &g, const edge_array< W > &len, array< mcb::spvecfp > &mcb, array< mcb::spvecfp > &proof, const mcb::edge_num &enumb, double error=0.375) |
| | Compute a minimum cycle basis of a weighted directed graph.
|
| template<class W> |
| W | mcb::DMCB (const graph &g, const edge_array< W > &len, array< mcb::spvecfp > &mcb, const mcb::edge_num &enumb, double error=0.375) |
| | Compute a minimum cycle basis of a weighted directed graph.
|
| template<class W> |
| W | mcb::DMCB (const graph &g, const edge_array< W > &len, array< array< etype > > &mcb, const mcb::edge_num &enumb, double error=0.375) |
| | Compute a minimum cycle basis of a weighted directed graph.
|
Undirected Minimum Cycle Basis |
The functions below are the more general implementation for undirected graphs. They also support multigraphs. As an underlying implementation they use the Support Vector approach (mcb::UMCB_SVA). They should be the first choice of use unless some special requirements exist.
|
| template<class W> |
| W | mcb::UMCB (const graph &g, const edge_array< W > &len, array< mcb::spvecgf2 > &mcb, const mcb::edge_num &enumb) |
| | Compute an MCB of an undirected graph (possible a multigraph) using the most general implementation of this library.
|
| int | mcb::UMCB (const graph &g, array< mcb::spvecgf2 > &mcb, const mcb::edge_num &enumb) |
| | Compute an MCB of an undirected graph (possible a multigraph) using the most general implementation of this library.
|
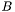 of
of  , that is a cycle basis of
, that is a cycle basis of  with the smallest length (sum of lengths of cycles). The basis is returned as an array of arrays of integers. Each such array if indexed on
with the smallest length (sum of lengths of cycles). The basis is returned as an array of arrays of integers. Each such array if indexed on 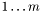 and its entry can be
and its entry can be 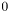 or
or 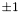 . Which edge corresponds to which index in this array can be found by the edge numbering, enumb. Note that the edge numbering using an indexing from
. Which edge corresponds to which index in this array can be found by the edge numbering, enumb. Note that the edge numbering using an indexing from 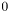 to
to 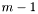 .
.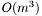 where
where 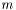 are the number of edges of
are the number of edges of  .
.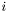 is the shortest cycle in
is the shortest cycle in 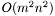 where
where 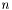 the number of vertices.
the number of vertices.  1.4.6
1.4.6