The Tralics software was designed as a tool for the Raweb. In this chapter, we explain some of our motivations. In the next chapter, we study some TeX commands and explain how they are handled in the same fashion by Tralics. Following chapters explain some differences, merely because XML is not dvi. In a final chapter, we explain how to configurate Tralics. There is a second part, that explains how the XML files can be used, converted into Pdf or HTML; it describes also the Raweb DTD. The last chapter of the second part describes additions to the program made since 2007.
A short history of the Raweb may be found on the Inria internal web site(note: ➳). The question concerns Inria´s Annual Activity Report, also known as “Rapport d´activité”, or “Annexe technique” to the RA or “annexes scientifiques” to the RA. This is a document, written by the research teams, at the end of the year N (October, November), and published in March of year .
Until the 1993 edition (published in 1994), only a paper version existed. A LaTeX model was used since 1987, designed by Jacques André then Martin Jourdan. See the reference [5], by Louarn in the first Cahiers Gutenberg.
In 1993, contacts were made with the Grif S.A. society, for the design of a SGML DTD and a LaTeX-to-SGML converter(note: ➳). As a result, Philippe Louarn was able to put on the web the RA (year 1994) in its HTML version(note: ➳). But this converter was judged too complicated (rules were too strict) and for several years, the HTML was directly produced from the LaTeX source, using latex2html.
In 1996, a working group (conducted by Albert Benveniste) gave new specifications: independent modules, grouped into ten sections, etc. A technical group was created (conducted by Gérard Paget), whose objective was to find a company that could sell a software (maybe using XML as intermediate language). None was found, but the design of modules (in LaTeX syntax) was well-defined by Laurent Pierron and José Grimm with the aid of Marie-Pierre Durollet and Jean-Claude Le Moal. For the Ra98, a Perl script did some preprocessing, splitting the LaTeX source into modules (one module per HTML page). The author wishes to thank all these people (including A. Quadrat), who gave him the idea to work on LaTeX and write a translator.
In 1999, the Scientific Annexes to Inria´s Annual Report were renamed RAWEB, to emphasize the role played by the Web (it is available as a CD-Rom, but no more printed by Inria).
In 2001, the Perl scripts mentioned above evolved into a LaTeX-to-XML converter (some ideas were borrowed from latex2html, which is also a Perl script). The main trouble was conversion from XML to Pdf, and we used tools from the TeX community (by S. Rahtz and D. Carlisle [1]) and pdfLaTeX. On the other hand, the images in the HTML files were converted by latex. Additional software (for creation on a global index, etc.) was written/used by Marie-Pierre Durollet.
This gave a complicated object: a Perl script, that converts a LaTeX file into XML (using Omega as a subprocess for the math) followed by another Perl script that extracts the math, calls latex, then dvips, then pstoimg (a Perl script that calls ppmquant, pnmcrop, and so forth, whose job is to produce a png image for the math formula), and finally an XSLT processor for the effective conversion. This became even more complicated in 2004, where a new DTD was introduced (designed by Bruno Marmol and people mentioned above), hence a XML-to-XML translator. See Figure 1.
 |
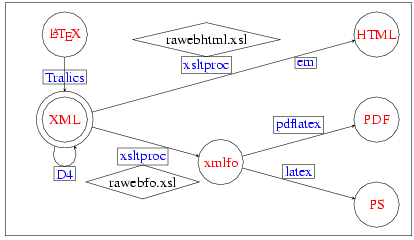The big Perl script was rewritten as a C++ translator, renamed Tralics, and got (for version 1.6) a first IDDN(note: ➳) number in December 2002. This software was still able to produce a LaTeX preview of the Raweb: The source is read, the syntax is tested, a LaTeX file is written for each module, latex and bibtex are called, the resulting dvi is converted to PostScript. But the same Tralics can be used in a different way: the source is read, the syntax is tested, an XML file is created, an XSLT processor is called to generate the XSL/Format, and pdflatex generates the Pdf (you can also generate an HTML version).
Since 2003, there are a few people writing their RA directly in XML. As a consequence, the new Tralics, that is used in 2004, does only the bare minimum: it converts the LaTeX code into XML code. There is a Perl script that does everything else (calling external programs like latex, xsltproc, etc). A non-obvious point concerns the math and the images. For the math, see above; for the images, a Perl script (the same as above) is used for conversion from PostScript to png. In some cases, the image already exists in png format and it is unwise to re-create it.
In 2007, the name of the Raweb changed; it is now RalyX. Here is a quote from the Web page:
The objective of the RalyX(note: ➳) project was to publish and exploit dynamically the annual INRIA activity reports; Ralyx is based on the Xylème(note: ➳) system, a native XML database. Xylème stores the XML version of the activity reports and supports queries to the reports involving both their structure and their content.
The first objective was to offer a tool for browsing the activity report with the same interface as the legacy HTML version. However, thanks to Xylème, pages and links are no longer statics, but computed on the fly, which can offer more flexibility in the future (different styles of display, editing along the year, etc).
The main objectives of Tralics are described in [3]. Recall that we want a program that converts from one language to another, such that
the result is easily analyzable,
the structure is preserved,
the translation is univocal.
By the very choice of the XML language as target, the first objective is automatically satisfied. The only little problem concerns spaces: in which cases are spaces used as delimiter or as text? The translation of `\par␣x{␣}{␣}x\par´ is `<p>x␣␣␣x</p>´, and this is often interpreted in the same fashion as a single space.
The third item has the following meaning: the translation of `\foo´ and `\bar´ should be different in case these objects have different meanings in LaTeX, but should be the same otherwise. One could argue that some tokens could be translated more than once in a different context (remember the \texorpdfstring command). We could imagine special rules for the bibliography; in fact, in math mode you must use a different function to add attributes to an element. On the other hand, we have an application where `\tt´ and `\bf´ are treated alike: in fact, all font information is removed, by redefining element names.
The important point is preservation of the structure. This means of course that the initial document has some structure and the target has one also. Clearly the structure of an XML document is given by its DTD, but this is completely ignored by Tralics. The first version of the program was very strict; nowadays, in your document, you can omit the `\documentclass´, the `\begin{document}´, or the `\end{document}´.(note: ➳)
There are some implicit rules, for instance that `\section´ terminates a `\subsection´, the occurrence of a character in vertical mode triggers the start of a <p> element, etc.
In [3], we wrote that the document should satisfy three kinds of of assumptions: some technical assumptions (like: there is no `\0´ in the document), some validity assumptions (the document can be compiled by LaTeX without errors, it respects the rules of the Raweb as given on the web pages), and more general, unwritten, rules. The current translator is more flexible: there is no restriction on the syntax of commands, except that null characters are not allowed, plain TeX documents are translated (for instance the file xii.tex by D. Carlisle that starts with \let~\catcode~`76 and ends with Yer.W,:jbye), and we have an application where only one part of the document is translated: only code before `\maketitle´ is used. In this document we shall explain these things.
The Tralics software is formed of five different types of files. On one hand we have the documentation; this is formed of a sequence of LaTeX documents (like the one you are reading), converted by Tralics into XML then HTML, together with a sequence of HTML pages that describe all commands, features, and packages. These files have no explicit Copyright notice (so that default rules apply). The distribution contains a lots of tools that can be used for the conversion from XML to XML, HTML, or Pdf, written by various authors, with different copyright notices.
The Tralics executable can be obtained by compiling the sources; some precompiled versions are also available. Some configuration files are also provided (files with extension .tcf, .clt, or .plt). The binary may contain a path to these auxiliary files, if this is not the case, the path must be given at runtime to the program. Sources are distributed according to the CeCILL Free Software Licensing Agreement. This gives anybody the right to modify the sources, redistribute the software, and include it (or part of it) into another Software (see the Copyright Notice for details).
Finally, the distribution contains some test files. These are examples of source code, and their XML translation. Most of these file compile without error, but some files test the error handling mechanism. These files are distributed under the same conditions as the source files, and it is assumed that whoever changes the sources modifies the test files accordingly.
Let´s consider the following piece of code.
$\left [1=2\right\}$ est une \emph{formule de mathématiques}~!
You would expect this to be understood by LaTeX as ` est une formule de mathématiques !´ but(note: ➳) the result is `Hello, world!´, since we have preceded it by this (curious) list of commands
\catcode`\$=\active\def$#1~{\catcode`\$=3 Hello, world} %$emacs
In TeX, translation depends on a great number of tables, that assign values to numeric or symbolic quantities. For instance, each character (a number between 0 and 255) in each font (for instance \OT1/cmr/m/it/10) is associated to its dimensions, ligature informations, etc. Our example (with a normal dollar sign) uses three fonts: a math font, an italic font and an upright font. Often, these tables are read only by TeX, in some other cases a user might look at them, and sometimes they are designed to be modified. For instance, the slant value of the current font is in general ignored (except by commands like `\emph´). A very important table holds the meaning of commands: they may be predefined (like `\left´), defined in a format (like `\emph´), or defined by the user (there are a great number of mathematicians that define a command named `\RR´ for the set of real numbers).
An important table is the table of category codes. Each character has a category code, an integer between 0 and 15. For instance, `e´ has category letter, `é´ has category active (so that it is equivalent to `\´e´)(note: ➳), backslash, open brace, close brace and dollar sign are of category 0, 1, 2, and 3 respectively. A command like `\left´ is formed by an introducer (any character of category 0, its value is irrelevant) and a sequence of letters (in the example, the space that follows is not part of the command, since its category code is 5; this space will be read again, and ignored, unless its category code changes; such a change can be triggered by the evaluation of the command); while a command like `\}´ or `\$´ is formed of an introducer and a single non-letter character (when followed by spaces, these spaces do not disappear). Writing a TeX scanner is easy, the only difficulty is that category codes can change (for instance, in verbatim mode). In the example, the tokens are the following: $3 left [12 112 =12 right {, etc, s11 }2 ~13 !12. Note that a closing brace, with default category code is shown as `}2´, while a command whose name is formed of a closing brace is shown as }. We use underlining in the HTML version, instead of boxing, as in the TeXbook. If you say \let\foo\bar, and ask Tralics for the meaning of \foo, as in \show\foo, it knows the name `foo´ of the token and its value (this is a command code) and gets the name `bar´ from a lookup table, and adds the current value of the escape character in front. If this is the plus sign, you will see +foo=+bar.
Parsing an expression means finding for each command its arguments. In the example, the two active characters é and ~ take no argument. The \active command takes no argument either. The \emph command takes one argument(note: ➳): a token, or a token list delimited by braces (i.e. characters with category codes 1 and 2), these braces are not part of the argument. The two commands \left and \right are special: they want a delimiter, in reality a pointer into a special slot in the current math font; the argument cannot be delimited by braces. The syntax of \catcode is more complicated. In fact, it is an instance of <codename>(note: ➳), and <codename><8-bit number> is something that can follow \the or be used as <internal integer>, while a <code assignment> is <codename> <8-bit number> <equals> <number>. We shall explain this in details later; the idea is that, depending on the context, the \catcode command returns a value stored in a table or modifies it. In the case of
\catcode`\$=\active
the <8-bit number> is the internal internal code of the dollar sign, expressed in the form ``\$´, and the <number> is another character code(note: ➳). Expanding a command means (roughly speaking) reading its arguments, and replacing it with the body of the command (where special markers like `#1´ have been substituted by the value of the arguments). In some cases, internal tables may be consulted, but they are never modified. Evaluating a command implies modification of some internal state variables (for instance, a character can be added to the current character list, or a complete paragraph split into lines, or a register modified). In this example, the dollar character becomes magically active: a dollar character is no more read as $3 but as $13.
The syntax of \def and friends is <def><control sequence><definition text> where <definition text> is <parameter text><left brace><balanced text><right brace>. In the case of
\def$#1~{\catcode`\$=3 Hello, world}
the <control sequence> is the dollar sign (the object to be defined, a command or, as in this example, an active character), the <parameter text> is everything before the open brace, here `#1~´, and the <balanced text> is everything between the braces. Evaluation of `\def´ consists in storing in a table the <parameter text> and the <balanced text> (TeX stores also a special marker representing the <left brace>). What happens now when TeX sees a dollar sign? since this character is active, the definition given above applies. The <parameter text> explains how to read arguments. In this case, `#1~´ means that there is one argument, everything up to (but not including) a tilde character. In the case of `$\left....$...}~!´, all characters are read (except the exclamation point). They are replaced by the body (no substitution is needed). After that, TeX sees \catcode and evaluates it as before, so that the dollar sign becomes a math shift character again. The space after the digit 3 disappears, and we are left with `Hello, word!´. Note: the example is given in French, first in order to show how 8-bit characters can be used, and also because, in English, there is no tilde before an exclamation point. In general, when a macro reads a delimited argument and sees an empty line instead of the delimiter, it signals an error of the form Runaway argument? Paragraph ended before $ was complete.
Translation difficulties. There are different kinds of LaTeX to HTML/XML translators. Some, like gellmu(note: ➳) use a syntax of their own; others, like tex4ht use TeX as preprocessor, thus understand the full syntax; there are translators like tth or hévéa that use a fixed (and efficient parser), or like latex2html (written in Perl) that use pattern matching, and global substitutions instead of sequential evaluation. Neither of these is perfect. We explain in this paper how Tralics deals with a certain number of problems.
In LaTeX, commands can be defined in five places:
In the Pascal source. In this case, the command is a primitive, for instance `\def´ or `\left´. No equivalent might exist in the target language (for instance, you cannot define anything in a XML document, the result of `\left´ is an attribute of the <mfenced> element that results of the translation of the group implied by \left. And what about \dump?)
In the format file. In this case, the command is defined in a file (for instance latex.ltx), analyzed by TeX and stored on disk using a fast retrieval method. For instance, plain TeX, LaTeX, ConTeXt have their own format file. Both plain TeX and LaTeX define a command named `\item´, in a different way, for the same purpose (the LaTeX command must be used inside a special environment, the plain TeX one can be used everywhere).
In a class file. A class file defines markup commands for a generic purpose (a book, an article, a presentation). For a book, you have a frontmatter, for an article, you can have a title page, in both you have sections, etc. The class defines also the current font, together with a lot of dimensions.
In a package. The difference between a class and a package was introduced by LaTeX2ϵ. Each document uses a single class, and lots of packages (this document uses the `report´ class, and the `RR´ package for the look; it uses `hyperref´ for hyper-links, `amsmath´ for the mathematical examples, `fancyvrb´ for the verbatim examples, etc.). Note that the plain TeX format provides a macro \proclaim for theorems, while the amsmath package provides a command \newtheorem for defining theorems.
In the TeX source, or files included via \input. The TeX source may redefine commands defined earlier; a package may redefine commands from the class, but should not redefine commands from other packages (i.e., the order in which packages are loaded should have no importance).
If one is to design a translator, the question is: which commands to translate? and how? Our idea is that all TeX primitives should be understood (the difference between `\dump´ and `\mydump´ is that you get either an Unimplemented or Undefined command error), as well as all standard LaTeX commands; of course all user-defined commands are expanded. Concerning classes and packages, our model (the Raweb) looks like a report. There are too many classes and packages for implementing them all. In earlier versions of the software, commands \documentclass {foo} or \usepackage {bar} did some action if the class foo or the package bar were known, and were ignored otherwise; we mentioned in the first version of this document interest in PhD thesis and slides classes, but no progress have been made in this direction.
In the current version of the software, commands \documentclass, \usepackage and all these are fully implemented. However, instead of reading foo.cls and bar.sty, Tralics reads foo.clt, and bar.plt. As an example, consider the makeidx package. The difference between the sty and plt files is in the definition of the \printindex command. The semantics of this command is: insert the index here. In the first version of Tralics there was no index, but nowadays multiple indexes (including glossaries) are allowed; the effect of the command is to mark a position in the XML tree, if omitted the index will be put at the end of the document; as a consequence, this cannot be a user-defined command. On the other hand, the LaTeX code asks to read the content of the index file (produced by makeindex) via \@input@; this a command that, as \@input, is used by LaTeX to read files that may be created after a first run (files of type aux, toc, bbl, ind, etc.), and is not implemented in Tralics (you run Tralics only once).
Another feature is worth mentioning. We have shown above some syntax rules; the source document uses the command \syntax, that takes one argument and put brackets around it; we followed Knuth´s notations and used the character \langle. This produces a math formula with a single character and my my favourite Web browser (in non-MathML mode) produces an ugly result, so that a simple less-than sign has been used for the HTML version. You can define a command \iftralics in the same way as \ifpdf (checking for instance that \tralicsversion is defined), and write conditional code (an example will be given later). But we used the opportunity provided by Tralics that, if your file is myfile.tex, myfile.ult is read before the TeX source (by Tralics, and not LaTeX) and this file may contain command redefinitions (of course, if you want to redefine a not-yet-defined command, some care must be taken).
Let´s assume that \foo is a command defined in one of these LaTeX files. Should it be translated by Tralics? and how? Notice first that a user command is always expandable, and has to be expanded; only the input stream is affected by this operation that consists in reading arguments and replacing them by an instantiated body. On the other hand, evaluation may modify or use internal tables, which can be implemented differently in our translator than in TeX (for instance, in pdfTeX, there is a way to re-use an image). Whenever a command is defined in a style file(note: ➳), we could use the LaTeX source. In some cases, for efficiency reasons, we implemented them in C++ (for instance, the whole fp package has been re-written).
A typical example is the \it command. This is a non official LaTeX command (see [2], or [6, section 7.3.6]): “it is legitimate for you to redefine them in a package or in the preamble according to your personal taste”. In Tralics, there is no difference between `\it´ and `\normalfont\itshape´. What these commands do in LaTeX is rather complex: essentially, some variables are set and `\selectfont´ is called. These commands are robust: if you use `\it´ in a chapter title, the toc file(note: ➳) will contain the name of the command, not the result of the expansion. Since Tralics does not write anything in a toc file, this feature is not implemented. Using font changes in a title is not recommended: look at the table of contents for this section. You will see that the word `Translation´ is in a different font, although it is the same in the main document. The command \texorpdfstring has been used, otherwise pdfTeX complains with Token not allowed in a PDFDocEncoded string, because font changes are forbidden in bookmarks.
Consider now a command like \motscle. This is defined by the Raweb as an environment (you can use it in Tralics only as an environment) and it expands to something like `{\bf mots clés}~´. We do not want Tralics to use this expansion. One reason can be that the post-processor might prefer something like `\textbf{Mots clefs}~:´ (i.e., use an alternate spelling, use an initial capital, add punctuation, etc). Another reason is that, since 2003, the Raweb is in English, and the translation should be an English word. For this reason, the translation of \motcles is <keywords>. The raweb class file contains commands that should not be translated: for instance, there is a command \ra@finpart whose purpose is to add a period after the last keyword. This should not be done by the translator, but by the program that will typeset the XML result.
Some TeX primitives are hard to translate. For instance the \´ command is assumed to put an acute accent over a character. It is defined (via an indirection through font encoding tables) in terms of the \accent primitive. We could translate \´ into a Unicode combining character (U+301, to be placed after the character, see [7, paragraph 7.7]). But in general, we have a construction like \´e which is defined in iso-latin1, this is the Unicode character “latin small letter e with acute”. In the same fashion `\k a´ translates to `ą´, this could produce `ą´, but the actual translation by Tralics is `ą´. In a previous version of Tralics, a construction like \´\^ was illegal. In the current version, we use a double indirection table. You can typeset the name Hàn Thế Thành of the author of pdfTeX, the input is Th\´{\^e}, the Tralics output is Thế. If you know the Unicode character value, you can enter it (in Tralics as Th^^^^1ebf or as Th\char1EBF).
A construction like `\font\myfont=cmt10 at 13pt´ defines a command \myfont that can be used as {\myfont \char217w}. The effect of this command is to pick up two characters from the font cmt10, scaled by some ratio (it depends on the “at” size of the font), and typeset them. Note that the font could specify a ligature, so that the result could be a single character. In any case, the result might look very different from `Ùw´ (for instance LaTeX provides a font containing only lines or circles). In the current version of Tralics, translation does not depend on the current font. The only interest of changing the current font with \font is that you can access or modify the internal tables of the font (but no metric file is read at all by Tralics).
In order to translate font changes correctly, you should define a command, for instance \myw, that uses character w, of the font `myfont´; the command could be more elaborate (it could look at the slant of the current font and select a slanted version of the character); the command could then be redefined for Tralics, either using a Unicode character, for instance \char"1E09 if you want a C with cedilla and acute, or something else if the character is not defined by Unicode.
A category code is an integer between 0 and 16, as explained in the TeXbook; it is an attribute of a character, as used by the tokenizer. The codes are used according to the following table.
A character of category code 1 serves as group delimiter (opening character), as well as delimiter for macros and token lists. It is a <left brace> as used in the rules explained above. By default, the left brace character { is the only one with category 1.
A character of category code 2 serves as group delimiter (closing character), as well as delimiter for macros and token lists. It is a <right brace> as used in the rules explained above. By default, the right brace character } is the only one with category 2. The end of `verbatim´ environment is handled by the following piece of code, that shows how to change the category codes of the three characters mentioned above, and use alternate characters for the same purpose.
\begingroup \catcode `|=0 \catcode `[= 1
\catcode`]=2 \catcode `\{=12 \catcode `\}=12
\catcode`\\=12 |gdef|@xverbatim#1\end{verbatim}[#1|end[verbatim]]
|endgroup
A character of category 3 serves a math shift character. By default the dollar character `$´ is the only character in this category. The same character can be used to start and end a formula. Two consecutive character of category code 3 are used to start or end display math; the characters need not be the same.
A character of category code 4 is used as delimiter in arrays; it indicates the end of a cell. A typical row in a LaTeX array is a&b&c\\; in plain TeX, it would finish with \cr or \crcr. The & character is the only one of category code 4.
A character of category 5 is a end-of-line character. When such a character is seen, all remaining characters on the current line are ignored. After that, the reader behaves as if it had seen nothing, a space, or a \par token. In some cases, the \par token is invalid. In Tralics, this space character is special, in that it may print as a new line character, in TeX, it is a normal space. By default, only the carriage return character is of category code 5 (this character is inserted at the end of every line, instead of the line feed, carriage return, or both, that marks the end-of-line in the file).
A character of category 6 can be used as delimiter in a command, or a table preamble. By default, there is one character of this category, the `#´. A typical array preamble is `\indent#\hfil&\quad#\hfil\cr´ (this is the first example of \halign in the TeXbook. We shall not describe TeX arrays here).
A character of category code 7 is a superscript character; by default, it is the hat character. Do not confuse it with \^ that produces an accent. Such a character can be used only in math mode. There is also the double hat construction, explained later in section 5.1: two identical characters of category code 7 can be used to read any 8bit character as in ^^ab; in Tralics, a 16 bit character can be read using 4 such characters.
A character of category code 8 (by default the underscore character) can be used as subscript character; as in the case of superscript characters, you can use it only in math mode.
A character of category code 9 is ignored. Tralics ignores no character by default. On the other hand, it cannot put a null character in a string, so that the null character will not appear in the XML output (note: the same holds for \char0 and ^^00).
A character of category 10 behaves like a space. By default, space, tabulation, character 160 behave like this (note that the character 160 is no-break space, it should be equivalent to ~).
A character of category code 11 is a letter. By default, only characters in the range `a´ to `z´ and `A´ to `Z´ are of category 11.
A character of category 12 is an `Other character´. All characters not listed here are of category 12, including all digits.
A character of category 13 is an active character. Currently, there is only one active character, the ~. An error is signaled in the case where an active character is used, but undefined. Tralics defines _, # and &, to be the same as \_, \# and \&.
A character of category code 14, is a comment character: all characters remaining on the current line are discarded. By default `%´ is a comment character.
A character of category code 15 is invalid. By default, all characters are valid.
A character of category code 16 is a `short verb´ character. This is a feature that does not exist in TeX. If you use \DefineShortVerb to make it a short verb, you should undefine the character before changing its category code. Unexpected results can follow if non-ASCII characters are of category code 16.
A character of category code 0 is used to create a command like \foo or \\; the associated token is foo or \; the value of the character is irrelevant. By default, there is only one character of category 0, the backslash.
In version one of this document, we started with category code 0, decremented the `enumi´ counter by one, before the first item, so that the first item label was zero. However Tralics does not use this counter in a `enumerate´ environment. Hence, the easiest solution, for having the same labels in the Pdf and HTML version, was to move this item to the end of the list.
If a TeX file contains the following lines,
\show{ \show} \show$ \show& \show# \show^ \show_ %$
\expandafter\show\space \show a \show 1 %
\def\foo+{}
\foo{ \foo} \foo$ \foo& \foo# \foo^ \foo_ \foo a \foo1
then Tralics will print:
begin-group character {.
end-group character }.
math shift character $.
alignment tab character &.
macro parameter character #.
superscript character ^.
subscript character _.
blank space .
the letter a.
the character 1.
In any case, we have a prefix that depends on the category code, then the value of the character. All calls to the command \foo are wrong and signal an error. We show here the first error message, followed by the “got” part of the other error messages. It is important to remember that the command has to be followed by the right token, or the right character with the right category code.
Error signaled at line 20 of file txt6.tex:
Use of \foo doesn't match its definition;
got {Character { of catcode 1},
expected {Character + of catcode 12}.
got {Character } of catcode 2}
got {Character $ of catcode 3}
got {Character & of catcode 4}
got {Character # of catcode 6}
got {Character ^ of catcode 7}
got {Character _ of catcode 8}
got a
got {Character 1 of catcode 12}
Translating mathematical formulas is rather difficult: this is because mathematics are complex in both TeX and MathML. Basically, you start with kernels, add some decoration, and connect these things. Kernels can be letters like x, y, z or A, B, C, but you see very often Greek letters like α, β, Γ, Δ, Hebraic characters like ℵ, old German, like ℘. Decoration can be, like in , a second kernel on the left, the right, above, below. People use also bars, dots, rings, arrows, etc. There are different types of connectors: for instance you can say or , using parallel bars, or , using crossing bars. Amstex was designed by Spivak for easy typesetting of tensors of the form .
The first difficulty consists in representing all these symbols. In TeX, you use commands like \alpha, defined as \mathchar"10B, whose effect is to chose a character from a font (depending on the packages used; a big difficulty is to chose math fonts that go well with the main text font of the document). Some characters exist in bold version, or in italics version. A non trivial question is how to put everything in bold: you could use commands like \boldx \boldequals \boldalpha. It would be simpler to say \bold{$x=\alpha$}. One solution is to say `\boldmath´(note: ➳), or equivalently `\mathversion{bold}´ before starting a math formula; the effect is to use a bold version of everything (in fact, of all characters that use one of the math families, but the number of families is so small that not all symbols use this mechanism). You can say `\mathbf{x}´ or `\bm{x}´ in a math formula. Only \mathbf is implemented in Tralics, it provides a bold upright font; on the other hand, the \bm command is defined in the bm package; provided that fonts are available, it should use a bold version of everything (at least for all characters for which a bold typeface exists).
Traditionally, uppercase letters were upright, lowercase letters were
italics. This is the default for Greek letters, but TeX uses italics for
Roman letters; digits are by default upright uppercase, but lower case
digits (also known as “oldstyle numbers”) can also be used.
There are some
exceptions to these rules: an operator like \sin is typeset using upright
font. As said above, \mathbf produces upright characters. The so-called
“black board” or “double-struck” characters obtained
by \mathbb are upright, for instance
. An interesting point: lots of people prefer
, using \mathbbm. Some people fake it as
, using $I\!\!R$. You can always use \mathrm for an upright
character, as in $\mathrm{E}=mc^2$.
Some packages provide italic
uppercase Greek letters, and upright lowercase. Then
you can apply the Laplace operator
to the Delta function like this: .
This is shown in the dvi file as 
.
In MathML, characters should not be used directly. For instance, you should use <mn>125</mn> for a number, <mi>Foo</mi> for the variable Foo and <mo>sin</mo> for the operator sin. These elements have a mathvariant attribute, which indicates which variant to use. In the case <mo>, the default is upright; in the case <mi>, the MathML norms says: “The default mathvariant would (typically) be normal (non-slanted) unless the content is a single character, in which case it would be italic.” So we could translate \mathbb{R} as an <mi> element containing a normal R with a mathvariant attribute of value doublestruck. An alternate solution consists in using a double struck character R, and no mathvariant attribute. Here are all the possible variants, and for the character A its Unicode value: normal, bold (1D400), italic (1D434), bold-italic (1D468), double-struck (1D358), bold-fraktur (1D56C), script (1D49C), bold-script (1D4D0), fraktur (1D504), sans-serif (1D5A0), bold-sans-serif (1D5D4), sans-serif-italic (1D608), sans-serif-bold-italic (1D63C), monospace (1D670). In the case of Greek letters, Unicode knows the following variants: bold, italic, bold italic, sans-serif bold, and sans-serif bold italic. And in the case of digits: bold, double-struck, sans-serif, sans-serif bold, monospace. Your browser should show these characters as
Note: there are some holes in the table, starting at 1D400. For instance
the Laplace symbol (U+2112) looks like ,
but the
the translation of \mathcal
(that TeX shows as ), is not 1D49C+11 (this character does not
exists). The dvi file shows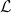 
and 
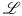for these symbols.
Another special case: there are some variants of the Greek letters
ϵ and ε; which one is the default is unclear.
There are two complementary views of MathML: presentation and content. This is how you would convert using content markup: <reln> <eq/> <ci> a </ci> <ci> b </ci> </reln>. And this is how Tralics converts the same using presentation <mrow> <mi>a</mi> <mo>=</mo> <mi>b</mi> </mrow>. A more complex example, in presentation mode:
<apply> <int/> <bvar><ci>x</ci></bvar> <condition> <apply><in/><ci>x</ci><ci type="set">C</ci></apply> </condition> <apply><sin/><ci>x</ci></apply> </apply>
You can clearly see that we apply the <int> operation to some quantity (in which <sin> is applied to x), subject to some condition (in which <in> is applied to x and some set). If you consider the expression $\int_0^\infty \sin(x)dx$, it is translated by Tralics as
<msubsup><mo>∫</mo> <mn>0</mn> <mi>∞</mi> </msubsup> <mrow> <mo form='prefix'>sin</mo> <mo>(</mo> <mi>x</mi> <mo>)</mo> <mi>d</mi> <mi>x</mi> </mrow>
Forget about the <mrow> element, this is added by Tralics using some heuristic rules that do not always work; their effect is to isolate the parentheses from the integral sign: the height of the parentheses should be normal. In the expression, one can see that the integral sign is a character considered as an operator (there no <int> element here); it has an exponent and an index. In the same fashion, \sin is translated as a <mo> element (with an attribute that says it precedes its argument). Nothing in the formula says that the argument is x.(note: ➳) Nothing says that `´ is not the product of d and x, but a conventional way of indicating that x is the bound variable (the <bvar> above). In fact, Tralics cannot guess the use of the tokens, it knows only the layout: for instance, is a Christoffel symbol with three indices or a randomly Greek letter, with two indices raised to some power? And what about or this footnote?(note: ➳) Note that such expressions are not part of content markup: in both cases, these things look like tensors and are to be produced with <mmultiscripts>. In what follows, we shall speak only of the presentation part of MathML.
Some features are difficult to implement. For instance, it is possible to group some equations in a single mathematical formula, and put a label (with a reference like 17) to the whole, as well as a label for each subequations (referenced as 17.a, 17.b, etc). It is also possible to split an equation on more than one line, with a single number for it:
It is possible to add some lines of text between two equations
| (1) |
What Tralics produces in this case is a single table (with a single equation number), and the intertext is just a new row, left aligned, that spans two columns (see \intertext in section ✻).
Horizontal spacing in math formulas in managed intelligently by TeX. In the case of or , there is some space on each side of the operator, and this space disappears when the formula becomes an exponent or an index. Here is an example.
that shows as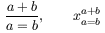 
in the dvi file.
Each operator has a type, and the value of horizontal spacing depends on the
type of the tokens on the left and the right. Traditionally, parentheses are
removed around the arguments of sine and cosine, and you say: sine squared of
X instead of sine of X, the whole squared. Example:
In TeX, you can consider every expression (a simple atom, or a list in braces) as an operator, provided that it is preceded by its type. Types Over, Under, Acc, Rad, Vcent are obtained by construction (overline, underline, adding an accent, constructing a radical, vertical centering). Types Ord, Op, Bin, Rel, Open, Close, Punct, Inner are obtained by defining characters via \mathchar, or using the following commands \mathord, \mathop, \mathbin, \mathrel, \mathopen, \mathclose, \mathpunct, \mathinner. These commands are understood by Tralics, but in general ignored. In the case of an inline expression, a line break can only appear after an operator (like plus or equal), provided it is the main operator (in particular, if you put the whole expression in braces, no line break will occur). This is ignored by Tralics. Hence something like cannot be broken(note: ➳).
Note that exponents and indices use a smaller font size, and exponents in
exponents use an even smaller one: compare with
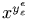. The image was obtained by converting the math
formula into XML, then in a png image (such kind of images will be put into
HTML pages, because there are few HTML browsers that understand MathML. We
used
anti-aliasing, because this is supposed to increase readability).
There are
three sizes, and four styles (\displaystyle,
\textstyle, \scriptstyle, and
\scriptscriptstyle). The first two styles in the
list have the same size (in MathML, there is an attribute scriptlevel that
controls the size of the expression, and another one, displaystyle,
that says
if the expression is in display style or not). In fact, TeX has two substyles,
cramped or not. Consider carefully the placement of exponents in the following
example
this is shown as 
in the dvi file.
One problem (for a translator like Tralics) deals with the placement of arguments versus operators. For instance, if you want to put a dot over a letter, you can say $\dot x$ (compare the math version and the text version ẋ; in text mode, slants are taken into account). The MathML equivalent is an <msup> whose first element is the identifier x. If you want to put a prime after a letter you say x´, or x^{\prime}. If you want to put an arrow over x prime, you have the choice between and . With the fonts used in this example, the first solution looks horrible. You can say x_2^3 or x^3_2: the result is the same: a math item, formed of a nucleus, a superscript and a subscript. If you want something like , you have to use two items, the first one has an empty nucleus, the second has no scripts. You can say , using three items. The MathML translation should consist in a single <mmultiscripts> element. It is possible to enclose a formula by braces, brackets, etc, provided that the font contains the machinery needed for it. You can either use \big and its variants, if you know the height of the formula, or \left and \right, or as in the example that follows, use an environment like matrix that uses whatever is best.
The \over command (and friends) are discouraged by amstex: you get a message of the form Package amsmath Warning: Foreign command \over; \frac or \genfrac should be used instead. In fact the command takes two arguments, one before and one after. Example
x=\left( a+b \over c+d\right)^2+1 gives
The trouble is the following: Assume that we have a command \myfrac that typesets its arguments as if the current style is script or scriptscript, and otherwise. In an expression as above, the current style cannot be known before the \over is seen. For this reason, TeX introduced a command \mathchoice that takes four arguments, one for each style; after TeX has completely read the math expression, it takes, in a second pass, the relevant token list. This is complicated. This mechanism is partially implemented in the current version of Tralics.
If you do not like MathML, you can set the integer \@nomathml to a non-zero value. If it is positive, then most math commands are allowed outside math mode, with trivial translation. If it is negative, then math formulas are parsed as usual, but the resulting tree is output à la TeX, rather than producing a MathML formula. Example
\makeatletter
\@nomathml=1
\sqrt{\alpha+\beta ^4}
\@nomathml=-1
$\sqrt{\alpha+\beta ^4}$
The translation is
\sqrt \alpha +\beta ^4
<texmath type='inline'>\sqrt{\alpha +\beta ^4}</texmath>
Assume that we have a number, say `1.3´, and want to convert this to a dimension, say `1.3pt´. If the number is in a command \foo, we can say \dimen0=\foo pt. On the other hand, how can we get 1.3 given that \dimen0 holds 1.3pt? We may use \the\dimen0, and remove the last two characters. Hence we say \expandafter\rem@pt\the\dimen0. One trouble is that the category codes of the characters `pt´ produced by the \the command are 12, not 11, so that a definition like
\def\rem@pt#1pt{#1}
does not work. You could try to change the category codes of p and t in the definition, but these letters are part of the name of the command. Some black magic has to be used. The code shown here converts also `12.0pt´ to `12´.
\begingroup
\catcode`P=12
\catcode`T=12
\lowercase{
\def\x{\def\rem@pt##1.##2PT{##1\ifnum##2>\z@.##2\fi}}}
\expandafter\endgroup\x
Implementing such a construction in a Perl script is not obvious. Consider then the following example:
\def\foo#1{#1x#1}\def\xbar#1{ $#1$}
\expandafter\foo\xbar y
\foo\xbar y
Consider line 2. After \expandafter has read the two tokens \foo and \xbar, current state is S, a space and the character `y´ are not yet read. Expansion of \xbar reads as argument the character y; the space before it is ignored. The expansion is then foo ␣5 $3 y11 $3. Hence the argument of \foo is the dollar sign, expanding it gives $3 x11 $3 y11 $3. Note that this gives an odd number of dollar signs.
Consider now the third line. Here the argument of \foo is \xbar. The expansion is xbar x11 xbar, and a space and `y´ have to be read. The expansion of \xbar is ␣5 $3 x11 $3. The second \xbar reads a space and `y´ as its argument. The expansion is ␣5 $3 y11 $3. Note that latex2html complains with: Unknown commands: xbarx, because the string is rescanned, and a space should have been added. In the second version of our translator, which was a Perl script as latex2html, we solved this problem as follows. The commands \\ and \! are replaced by \00! and \01!, special characters are replaced by \3#!, \3&!, \3<!, \3>!, and \3~!. A command like \foo is replaced by \1foo!, spaces after \foo are removed. Using such a mechanism, we can handle spaces correctly, as long as the category codes do not change.
The current version of Tralics uses the same representation as TeX for its tokens, namely an integer. A character token like $3, is represented by the integer , where N is the number of characters, c the character value (here 36), and C the category code (here 3). In TeX, the constant N is 256, in Tralics, it is . Let ; then non-character tokens are integers x at least M, and is the address in the table of equivalents. An active character is represented by , with , and a single-character command is represented by with ; multiletter control sequences are represented by integers larger than , and is the hashtable location of the token (it contains the name of the token).
If you say \uccode`\~=`A two integers are read; in these case, they are character constants; the value is obtained by taking the token modulo N. If you say \uppercase{~}, for each token in the list, something happens if the value is less than ; if the value modulo N is c, and if the upper case equivalent of c is , a non-zero value, then is used instead of x. Note that if and , then , this means that an active character is replaced by an active character, a character with category code C is replaced by a character with the same category code.
The behavior of a token is determined by its command code (and its subcode): if the token is , then C is the command code, and c the subcode. Said otherwise, for a character token, the command code is the category code, and the subcode is the character value. In the other case, the token is non-constant, its meaning can change. The actual meaning is in the table of equivalents, it can be pushed on the save stack. For instance, the default value of \count is (1,90,0). Here the first integer is the definition level, (1 is the bottom level), 90 is the command code, namely register, and 0 is the subcode. The default value of \pausing is (1,91,324), where the second number is the command code assignint and the third number an address in the table of integers. Remember that, in the case of \the\count0, the \count command is evaluated for a value; in all other cases it is evaluated for side effects. In particular for a case like \global\count3=17. Assume that you say \count3=17; in such a case a number is read, namely 3, and checked for out-of-range. After that, the subtype is looked at (the commands \count, \dimen, \skip, or \muskip have the same command code, but different subtypes, they read something and store it somewhere). Note: if you say \countdef\foo3, then \foo has assignint as command code, and its subcode is 3, thus behaves exactly like \pausing. Moreover the action is the same as \count, after 3 has been read. In the same fashion, if you say \chardef\bar3, then \bar has chargiven as command code, and its subcode is 3; the action is exactly the same as \char, after 3 has been read. In the case of chargiven, the action consists in putting the character in the dvi file (Tralics puts in the XML tree). In the case of assignint, a integer is stored or retrieved. For instance, \foo=17, and \count3=17 read a number 17. This number will be stored somewhere in the eqtb table; the location is 3 slots after the start of the \count table. This slot contains (L,V), for instance (4,23). The first number is the definition level, and the second is the value. In the case L=0, this means that the object is undefined (in the case of a counter, this means zero). Otherwise this is the level. In the case A{B{C}}, A is at level 1, B at level 2, and C at level 3. The quantity L is never greater than the current level. In the case where the assignment is global, (L,V) is instantiated to (1,17). In the case where the current level is L, then V in (L,V) is replaced by 17. Otherwise, the old value is saved on the stack, and (L,V) is replaced by (l,17) (where l is the current level). When the group is closed, the old value is restored.
Note the following trick. Assume that \A increases some counter and puts the value in \foo, \B does the same, but changes globally \foo. Assume that you say {\A\A\B\B\A\A...}. The first \A sets \foo to 1 and saves (0,undef). The second \A sets \foo to 2. The first \B sets \foo to 3 at level 1, the second \B sets \foo to 4, level unchanged. The next \A saves the old value of \foo and sets \foo to 5, etc. As a consequence: every \A preceded by a \B will put an item on the save stack. When the stack is restored, the value to restore will be and the current value . If is 1, nothing happens. Otherwise, is replaced by . As a consequence the value after the group is the value of the last \B. This results in a waste of the save stack. For this reason, Knuth says: all assignments to the scratch registers whose numbers are 1, 3, 5, 7 and 9 should be \global; all assignments to the other scratch registers (0, 2, 4, 6, 8, 255) should be non-\global.
A silly question is: what happens if you say {\let \endgraf \par \gdef\par{} \edef \foo {\endgraf} \Foo \def \endgraf {} \Bar }. In the current version of \Tralics, but this is also true for TeX, when you say \def\foo, the command code of \foo is changed to be user-defined, and the subcode is an address into a table containing the token list of the body. On the other hand, \let \foo \bar will use the command code and subcode of \bar, and copy this in \foo. In the original version of Tralics, the Perl version, we had two tables: the list of predefined commands, with their internal number, and the list of user defined commands with their body. In the code above, when \Foo is executed, then \foo is a user defined command, whose body contains \endgraf, whose meaning is the original \par. When \Bar is seen, the meaning of this token has changed. The essential reason why Tralics was re-written in C++ is to make this piece of code work.
Most TeX formats (plain, LaTeX, amstex) have been written by American people; nowadays, major developments are done in Europe (including the conTeXt format, and the hyperref package). However, lots of people use basic primitives for their French publications, and the situation is not simplified by the fact that there are two packages for writing French documents (one by late Bernard Gaulle, and one by D. Flipo).
In the original version of TeX you had to say `\´e´ for an e acute, and you had to say `\c c´ or `\c{c}´ for a c cedilla (which form being the best is in general unknown). For homogeneity reasons, Lamport recommends \´{e}. Because some accents are redefined by tables, or tabular environments, the solution that always works is \a´{e}. This is something strange, but a translator like Tralics has to cope with it (for instance, some authors of the Raweb use BibTeX files that are generated automatically from a data-basis, and this software systematically produces \a for accents). This makes texts rather uneasy to read, and not every spell-checker understands this (Ispell for instance allows José or Jos\´e, but not both). By default (i.e. on Linux machine) LaTeX understands iso-8859-1. This means that all characters used in France are recognized (except, œŒŸ, these characters cause also problems in HTML). Recently, another character was introduced, namely €. Nobody knows how to use it (according to [6, paragraph 7.8.7], published in april 2004, \texteuro is the official LaTeX way, it is translated by Tralics as AC;). In case of doubt, you should use `euro´.
In order to emphasize words, you can underline them, use a different font, or mark them with quotes. In English, you would use quotes “like these” or `like these´, but never like “this”. In France, guillemets « are used like this ». Note that the spacing is different from English, but the package should take case of everything. The forever question is: how to enter these funny characters in my keyboard made in Mexico(note: ➳). One solution consists of typing two < in a row and hope for the best (we have either an active character, or a ligature). Note that Tralics translates \verb+<<-->>+ as <hi rend=´tt´><​<​-​-​>​>​ </hi> the funny characters have as only purpose to inhibit ligatures in the resulting XML(note: ➳). The result might also be: ¡¡ and ¿¿. Depending on the packages, you should perhaps use \guillemotleft, \guillemotright or \og, \fg. Which method is the best is still unclear to me.