page
suivante | publications
professeur agrégée de
mathématiques
collaboratrice extérieure du
projet Lemme depuis octobre 1998
détachée à l'INRIA depuis septembre 2002
Thèmes de recherche
Etant professeur de mathématiques, je
m'intéresse aux démonstrations interactives sur
ordinateur et
plus particulièrement à la possibilité d'utiliser
un assistant
à la preuve dans l'enseignement des mathématiques.
L'équipe du projet Lemme utilise principalement le
système de
preuve Coq et a développé une interface graphique PCoq qui fournit des outils
pour manipuler des formules mathématiques et logiques.
Toutes mes activités de recherche sont axées autour du
système
Coq et sont effectuées en
collaboration avec les membres du projet Lemme.
- formalisation des mathématiques
Le but est d'étudier comment des théories
mathématiques peuvent être représentées dans
le système Coq, de façon
à être aussi lisibles et utilisables que possible par
quelqu'un qui en a une connaissance scolaire.
Je travaille actuellement sur la formalisation de la géométrie affine et
euclidienne enseignée au lycée.
- environnements de preuves pour des
utilisateurs enseignants et étudiants
Le but est de rendre les énoncés et preuves
en Coq lisibles par des
enseignants et les étudiants habituellement profanes
vis-à-vis de Coq.
1. Travail sur les
énoncés
J'utilise l'interface Pcoq, ce qui permet :
- d'afficher des formules mathématiques avec les notations
usuelles,
- de traduire en langue naturelle (français ou anglais) les
formules logiques représentant des énoncés.
|
|

exemple :
énoncé du théorème de la droite de Simson
tel qu'il apparaît à l'écran avec Pcoq
|
| |
Avec Loïc Pottier, nous avons
développé et intégré à Pcoq,
un outil de visualisation des énoncés
géométriques : GeoView. Il permet à partir
d'un énoncé de théorème en Coq
de générer la figure dynamique interactive correspondante
visualisée grâce à l'applet Java GeoplanJ.
|
|
figure
générée par GeoView
à partir du théorème de la droite de Simson
les points en vert peuvent être
déplacés à la souris
|
| |
Nous obtenons avec notre outil
GeoView des figures qui peuvent être
manipulées directement avec GeoplanW, logiciel utilisé couramment par les professeurs de
l'enseignement secondaire .
Les figures générées par GeoView
peuvent ainsi être utilisées et modifiées hors du
contexte de preuve.
Elles peuvent en particulier être intégrées dans
une page HTML en utilisant l'applet Java GeoplanJ, comme ici.
- les points en vert peuvent être déplacés à
la souris (bouton gauche),
- en maintenant le bouton droit enfoncé, on peut déplacer
la figure,
- en cliquant sur la figure et en utilisant les touches < et >,
on peut agrandir ou réduire la figure,
- en double-cliquant sur la figure, on obtient un menu : on peut
créer de nouveaux objets pour vérifier des conjectures
par exemple. |
| |
2. Travail sur les preuves
Pour rendre lisibles les preuves, nous avons avec Loïc Pottier,
développé un programme qui traduit un arbre de preuve (en
format interne à Coq) en XML.
Des outils en cours de développement permettent de visualiser
cet arbre XML sous différentes formes :
- script Coq,
- texte structuré d'explications en langue naturelle
(français ou anglais),
- schéma de démonstration, graphe
orienté acyclique dans lequel chaque pas de déduction est
représenté par un sous graphe.
Ce travail est réalisé avec Hanane Naciri dans le cadre du
projet européen MoWGLI. [Transparents] |
|
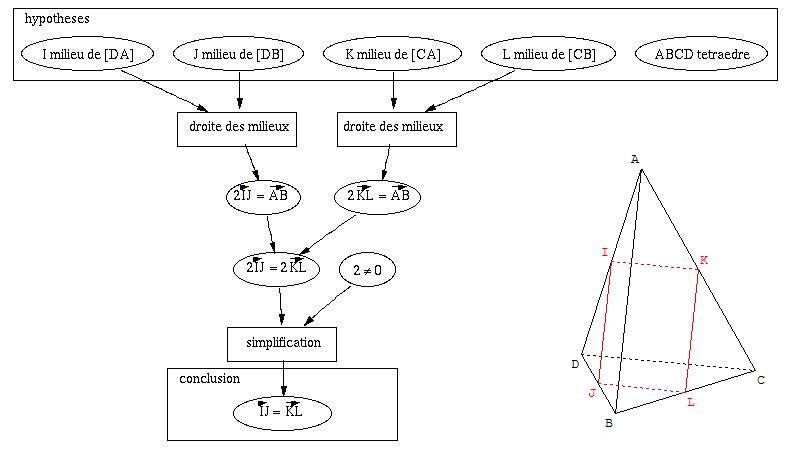
exemple :
schéma de démonstration d'un exercice de
géométrie spatiale
les hypothèses et la conclusion apparaissent
clairement en haut et en bas
le nœud "droite des milieux" correspond à l'application du
théorème dit "de la droite des milieux"
et "simplification" correspond à une simplification par un
réel non nul (ici 2)
|
| |
Conférences et
Publications [haut
de la page]
Frédérique Guilhot.
Formalisation en Coq et visualisation d'un cours de
géométrie
pour le
lycée, [Postcript] [pdf]
Technique et Science Informatiques, Volume 24, Langages
applicatifs, pages 1113 à 1138, Hermes Science, 2005
Résumé : Enseigner les
mathématiques aux élèves de lycée en
utilisant la démonstration assistée par ordinateur
devient un objectif
accessible dans un futur proche. Nous présentons dans cet
article une
formalisation en Coq de la géométrie enseignée au
lycée ayant la particularité
de présenter les définitions, théorèmes et
preuves très proches de ceux donnés
dans les cours de mathématiques. Pour rendre les textes formels
accessibles aux
élèves, nous utilisons une interface graphique et un
outil de construction
automatique de figure dynamique. Nous présentons dans cet
article plusieurs
exemples d'énoncés, démonstrations et figures
correspondantes puis abordons les
difficultés rencontrées dans ce travail.
Y. Bertot, F. Guilhot, Loïc Pottier.
Visualizing
Geometrical Statements with GeoView, [Postcript] [pdf] [Transparents]
Electronic Notes in Theoretical Computer Science, Volume 103, pages
49 à 65, Elsevier, 2004
Proceedings of Workshop User Interfaces for Theorem Provers
in connection with TPHOLs'2003, Rome,
Italy.
Abstract : We describe a tool that combines a general
theorem prover and an off-the-shelf interface for dynamic
geometry drawing to enhance man machine interaction involving
geometrical proofs. With our tool, we can edit the statements of
geometrical theorems, construct and verify their proofs with the
theorem prover, and visualize the statements using the drawing
tool. The key component is an algorithm that computes the data
needed to draw a construction from the formal statement of the
theorem. The paper includes somme examples of output from our
combined tool, called GeoView
Formalisation en Coq d'un cours de
géométrie
pour le
lycée, [Postcript] [Transparents]
Journées Francophones des Langages Applicatifs, INRIA,
Janvier 2004
Résumé : Ce papier décrit
l'expérience d'une formalisation en Coq de la
géométrie
enseignée au lycée. Pour privilégier le
raisonnement,
l'axiomatique choisie n'utilise pas la méthode analytique.
L'accent est aussi porté sur les problèmes de forme : en
utilisant l'interface graphique Pcoq et l'outil de construction
GeoView, il est possible d'afficher à l'écran des
énoncés et
des figures dynamiques proches de ceux utilisés au lycée.
Nous
présentons dans ce papier quelques exemples de preuves puis
abordons les difficultés rencontrées dans ce travail.
Frédérique Guilhot.
Premiers pas vers un cours de géométrie en Coq
pour
le lycée, [Postcript]
INRIA Rapport de Recherche RR.4893, Juillet 2003.
Résumé : Nous présentons
dans ce
rapport une bibliothèque de géométrie en Coq
dédiée à
l'enseignement au lycée. L'accent est porté sur
l'utilisation
de l'interface graphique Pcoq et sur l'outil de construction
GeoView qui permettent de présenter des énoncés et
des figures
proches de ceux utilisés au lycée. L'axiomatique choisie
pour
la formalisation n'utilise pas la méthode analytique. Nous
présentons quelques exemples significatifs de preuves puis
abordons les difficultés rencontrées dans ce travail.
Abstract : In this report,
we present a library dealing with geometry in Coq. This library
is dedicated to high-school teaching. We stress on using the
graphical interface Pcoq and the drawing tool GeoView. These
tools enable us to display statements and draw figures in the
same way as students do. We give an axiomatization of geometry in
a non analytic setting and present some significant examples of
proofs developped with . We eventually discuss the difficulties
encountered in this work.
Frédérique Guilhot.
Démonstrations avec Coq de théorèmes de
géométrie
plane, utilisant les angles orientés, [Postcript]
INRIA Rapport de Recherche RR.4356, Janvier 2002.
Résumé : Dans ce rapport, nous
présentons une formalisation en Coq de la théorie des
angles
orientés de vecteurs non nuls. En utilisant ces objets, nous
avons démontré en Coq des théorèmes
classiques de la
géométrie plane dont : le théorème qui
donne une condition
nécessaire et suffisante pour que quatre points soient
cocycliques, le théorème qui montre que les
symétriques de
l'orthocentre d'un triangle par rapport à ses cîtés
sont sur
son cercle circonscrit, le théorème de la droite de
Simson et
le théorème de Napoléon. Nous décrivons la
construction de
preuves en Coq qui suivent les démonstrations classiques de
géométrie, et les difficultés rencontrées
lors de ce travail.
Nous montrons que l'utilisation de l'interface Pcoq permet des
notations proches de celles des mathématiques.
Abstract : Formalization
of the theory of oriented angles of non zero vectors using Coq is
reported. Using this theory, some classical plane geometry
theorems are proved, among them : the theorem which gives a
necessary and sufficient condition so that four points are
cocyclic, the one which shows that the reflected points with
respect to the sides of a triangle orthocenter are on its
circumscribed circle, the Simson's theorem and the Napoleon's
theorem. Elaboration of proofs using Coq that followed the
traditional proofs in geometry, and the difficulties encountered
are described. Use of the interface Pcoq allows notations close
to mathematical ones.
haut de la page | page
suivante