Définition 2.3 (2B-consistance d'une contrainte)
Soit
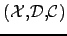
un
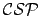
et
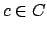
une contrainte k-aire sur les variables
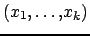
. On dit que la contrainte
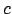
est 2B-consistante ssi :
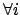
,
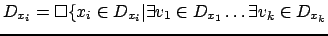
tel que
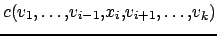
est vérifiée }.
La notion
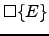
désigne la plus petite boîte contenant tous les éléments de l'ensemble
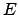
.
![\includegraphics[scale=0.6]{asympt.eps}](img170.png)